解析中考动态几何问题目

解析中考动态几何问题目

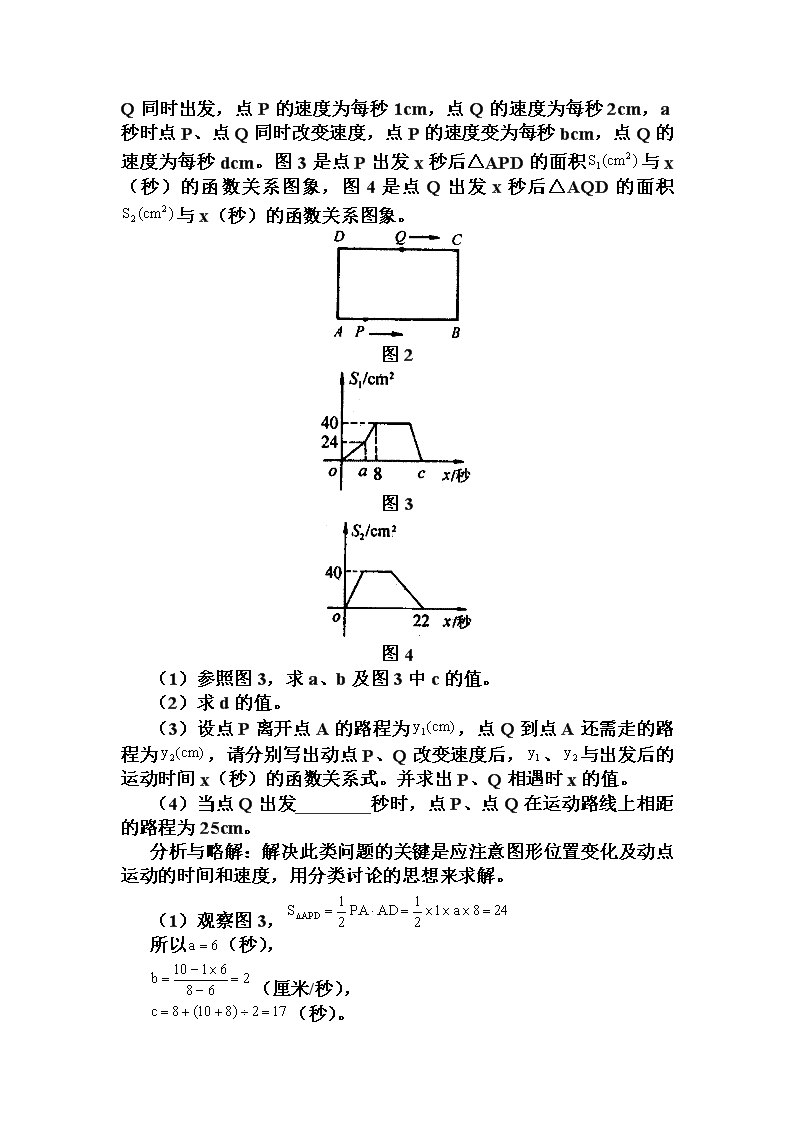
解析中考动态几何问题 霍晋兰 ‎ 动态几何题已成为中考试题的一大热点题型。在近几年各地的中考试卷中，以动点问题、平面图形的平移、翻折、旋转、剪拼问题等为代表的动态几何题频频出现在填空、选择、解答等各种题型中，考查同学们对图形的直觉能力以及从变化中看到不变实质的数学洞察力。‎ ‎ 解决动态几何题的策略是：把握运动规律，寻求运动中的特殊位置；在“动”中求“静”，在“静”中探求“动”的一般规律。通过探索、归纳、猜想，获得图形在运动过程中是否保留或具有某种性质。‎ ‎ 下面就动点型、动线型、动面型等几何题作一简要分析。‎ 一. 动点型 ‎ 1. 单动点型 ‎ 例1. 如图1，在矩形ABCD中，AD=12，AB=5，P是AD边上任意一点，PE⊥BD，PF⊥AC，E，F分别是垂足，求PE+PF的长。‎ 分析与略解：P是AD边上任意一点，不妨考虑特殊点的情况，即在“动”中求“静”。当P点在D（或A）处时，过D作DG⊥AC，垂足为G，‎ 则PE=0，PF=DG，‎ 故PE+PF=DG，‎ 在Rt△ADC中，‎ 由面积公式有：，‎ 再有“静”寻求“动”的一般规律，得到PE+PF=DG=。‎ 图1‎ ‎ 2. 双动点型 ‎ 例2. （2003年吉林省）如图2，在矩形ABCD中，AB=10cm，BC=8cm，点P从A出发，沿A→B→C→D路线运动，到D点停止；点Q从D点出发，沿D→C→B→A路线运动，到A停止。若点P、‎ Q同时出发，点P的速度为每秒1cm，点Q的速度为每秒2cm，a秒时点P、点Q同时改变速度，点P的速度变为每秒bcm，点Q的速度为每秒dcm。图3是点P出发x秒后△APD的面积与x（秒）的函数关系图象，图4是点Q出发x秒后△AQD的面积与x（秒）的函数关系图象。‎ 图2‎ 图3‎ 图4‎ ‎（1）参照图3，求a、b及图3中c的值。‎ ‎（2）求d的值。‎ ‎（3）设点P离开点A的路程为，点Q到点A还需走的路程为，请分别写出动点P、Q改变速度后，、与出发后的运动时间x（秒）的函数关系式。并求出P、Q相遇时x的值。‎ ‎（4）当点Q出发________秒时，点P、点Q在运动路线上相距的路程为25cm。‎ 分析与略解：解决此类问题的关键是应注意图形位置变化及动点运动的时间和速度，用分类讨论的思想来求解。‎ ‎（1）观察图3，‎ 所以（秒），‎ ‎（厘米/秒），‎ ‎（秒）。‎ ‎（2）依题意，‎ 解得（厘米/秒）‎ ‎（3）‎ 依题意，‎ 所以（秒）‎ ‎（4）1和19。‎ 二. 动线型 ‎ 1. 线平移型 ‎ 例3. （2004年河南省）如图5，边长为2的正方形ABCD中，顶点A的坐标是（0，2），一次函数y=x+t的图象L随t的不同取值变化时，位于L的右下方由L和正方形的边围成的图形面积为S（阴影部分）。‎ ‎（1）当t取何值时，S=3？‎ ‎（2）在平面直角坐标系下，画出S与t的函数图象。‎ 图5‎ 分析与略解：本题应抓住直线在平移过程中保持的位置关系和数量关系。‎ ‎（1）设L与正方形的边AD、CD相交于M、N，易证Rt△DMN是等腰三角形。只有当时，△DMN的面积是1，求得。‎ 所以时，S=3。‎ ‎（2）当时，；‎ 当时，；‎ 当时，S=4。图象略。‎ ‎ 2. 线旋转型 ‎ 例4. （2004年海口市）在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。‎ ‎（1）当直线MN绕点C旋转到图6的位置时，求证：①△ADC≌△CEB；②DE=AD+BE。‎ 图6‎ ‎（2）当直线MN绕点C旋转到图7的位置时，求证：DE=。‎ 图7‎ ‎（3）直线MN绕点C旋转到图8的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明。‎ 图8‎ 简析：本题在直线MN的旋转过程中，保持了△ADC≌△CEB这一性质。‎ 三. 动面型 ‎ 1. 面平移型 ‎ 例5. （2001年吉林省）如图9，有一边长为5cm的正方形ABCD和等腰△PQR，PQ=PR=5cm，QR=8cm，点B、C、Q、R在同一条直线L上，当C、Q两点重合时，等腰△PQR以1cm/s的速度沿直线L按箭头所示方向开始匀速运动，t s后正方形ABCD与等腰△PQR重合部分的面积为。解答下列问题：‎ ‎（1）当t=3s时，求S的值；‎ ‎（2）当t=5s时，求S的值；‎ ‎（3）当时，求S与t的函数关系式，并求出S的最大值。‎ 简析：此题是一个图形的运动问题，解答的方法是将各个时刻的图形分别画出来，则图形由“动”变“静”，再设法分别求解。这种分类画图的方法在解动态几何题中非常有效，它可帮助我们理清思路，各个击破。‎ 图9‎ ‎ 2. 画旋转型 ‎ 例6. 如图10，正△ABC的中心O恰好是扇形ODE的圆心，且点B在扇形内，要使扇形ODE绕点O无论怎样转动，△ABC与扇形重叠部分的面积总等于△ABC的面积的，扇形的圆心角应为多少度？说明理由。‎ 分析：本题属于动面型问题，先找到一种特殊情况，即重叠部分为△OBC时，，且此时∠BOC=120°，因此本题实际是扇形ODE由扇形BOC旋转得到的，∠FOG=∠BOC=120°，可证△BOF≌△COG，所以，故扇形的圆心角为120°。‎ 图10‎ 四. 翻折型 折叠类问题实际上是对称问题，解此类题目，应抓住翻折后的对称性及一些隐含的位置关系和数量关系。‎ ‎ 例7. 如图11，一张长方形纸片ABCD，其长AD为a，宽AB为b（a>b），在BC边上选取一点M，将△ABM沿AM翻折后B至的位置，若为长方形纸片ABCD的对称中心，则的值是 ‎___________。‎ 析解：连结BD。‎ 因为点为长方形纸片ABCD的对称中心，‎ 所以点一定在BD上，‎ 由翻折图形的性质可知 所以 所以△是等边三角形 所以