2010年北京市顺义区中考数学试题

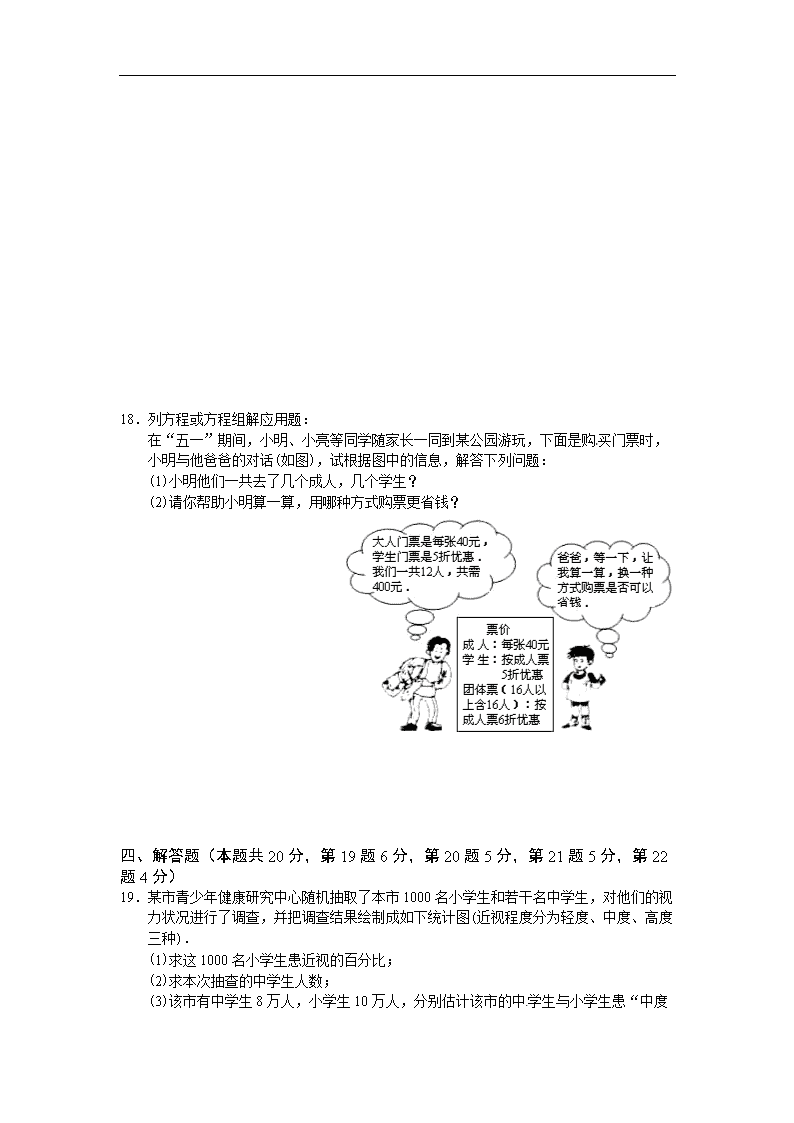
2010年北京市顺义区中考数学试题

‎2010年北京顺义区高中招生考试 数学试题 一、选择题（本题共32分，每小题4分）‎ ‎1．4的平方根是（ ）‎ A．2 B．±‎2 C． D．± ‎2．下列计算正确的是（ ）‎ A．x3＋x2＝x5 B．x4÷x＝x4‎ C．x3·x2＝x5 D．(x3)2＝x5‎ ‎3．从北京教育考试院获悉，截至‎2010年3月5日，今年北京市中考报名确认考生人数达10.2万，与去年报考人数持平．请把10.2万用科学记数法表示应为（ ）‎ A．0.102×106 B．10.2×‎104 ‎‎ C．1.02×105 D．1.02×104‎ ‎4．把a3－4ab2分解因式，结果正确的是（ ）‎ A．a(a＋4b)(a－4b) B．a(a2－4b2)‎ C．a(a＋2b)(a－2b) D．a(a－2b)2‎ ‎5．小明在做一道数学选择题时，经过审题，他知道在A、B、C、D四个备选答案中，只有一个是正确的，但他只能确定选项D是错误的，于是他在其它三个选项中随机选择了B，那么，小明答对这道选择题的概率是（ ）‎ A． B． C． D．1‎ ‎6．若一个正多边形的一个内角是120°，则这个正多边形的边数是（ ）‎ A．9 B．‎8 C．6 D．4‎ ‎7．某一段时间，小芳测得连续五天的日最高气温后，整理得出下表（有两个数据被遮盖）．‎ 日期 一 二 三 四 五 方差 平均气温 最高气温 ‎1℃‎ ‎2℃‎ ‎－‎‎2℃‎ ‎0℃‎ ‎1℃‎ 被遮盖的两个数据依次是（ ）‎ A．‎3℃‎，2 B．‎3℃‎，4 C．‎4℃‎，2 D．‎4℃‎，4‎ ‎8．点E为正方形ABCD的BC边的中点，动点F在对角线AC上运动，连接BF、EF．设AF＝x，△BEF的周长为y，那么能表示y与x的函数关系的图象大致是（ ）‎ A O B C O x O O O x x x y y y y A B C D A B C D F E 二、填空题（本题共16分，每小题4分）‎ ‎9．函数y＝中，自变量x的取值范围是 ．‎ ‎10．若|m－n|＋(m＋2)2＝0，则mn的值是 ．‎ ‎11．如图，△ABC内接于⊙O，已知∠ABO＝50º，则∠ACB＝ ．‎ ‎12．在平面直角坐标系中，已知点A(4，0)、B(4，10)，点C在y轴上，且△ABC是直角三角形，则满足条件的C点的坐标为 ．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：．‎ ‎14．解方程组 A B C D E ‎15．如图，AB＝AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，垂足为E．‎ 求证：AD＝AE．‎ ‎16．已知x＝2010，y＝2009，求代数式的值．‎ ‎17．已知正比例函数y＝kx(k≠0)与反比例函数y＝(m≠0)的图象交于A、B两点，且点A的坐标为(2，3)．‎ ‎(1)求正比例函数及反比例函数的解析式；‎ ‎(2)在所给的平面直角坐标系中画出两个函数的图象，根据图象直接写出点B的坐标及不等式kx＞的解集．‎ ‎18．列方程或方程组解应用题：‎ 在“五一”期间，小明、小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与他爸爸的对话(如图)，试根据图中的信息，解答下列问题：‎ ‎(1)小明他们一共去了几个成人，几个学生？‎ ‎(2)请你帮助小明算一算，用哪种方式购票更省钱？‎ 四、解答题（本题共20分，第19题6分，第20题5分，第21题5分，第22题4分）‎ ‎19．某市青少年健康研究中心随机抽取了本市1000名小学生和若干名中学生，对他们的视力状况进行了调查，并把调查结果绘制成如下统计图(近视程度分为轻度、中度、高度三种)．‎ ‎(1)求这1000名小学生患近视的百分比；‎ ‎(2)求本次抽查的中学生人数；‎ ‎(3)该市有中学生8万人，小学生10万人，分别估计该市的中 学生与小学生患“中度近视”的人数．‎ ‎[‎ A B C D ‎20．如图，在梯形ABCD中，AD∥BC，BD⊥DC，∠C＝60°，AD＝4，BC＝6，求AB的长．‎ B E F A O C D ‎21．如图，⊙O的直径AB＝4，C、D为圆周上两点，且四边形OBCD是菱形，过点D的直线EF∥AC，交BA、BC的延长线于点E、F．‎ ‎(1)求证：EF是⊙O的切线；‎ ‎(2)求DE的长．‎ ‎22．已知正方形纸片ABCD的边长为2．‎ 操作：如图1，将正方形纸片折叠，使顶点A落在边CD上的点P处(点P与C、D不重合)，折痕为EF，折叠后AB边落在PQ的位置，PQ与BC交于点G．‎ 探究：(1)观察操作结果，找到一个与△DEP相似的三角形，并证明你的结论；‎ ‎(2)当点P位于CD中点时，你找到的三角形与△DEP周长的比是多少？‎ B B A C D E F G Q P C A D ‎（备用）‎ 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23．已知抛物线y＝(k－1)x2＋2kx＋k－2与x轴有两个不同的交点．‎ ‎(1)求k的取值范围；‎ ‎(2)当k为整数，且关于x的方程3x＝kx－1的解是负数时，求抛物线的解析式；‎ y x O ‎4‎ ‎8‎ ‎－8‎ ‎－4‎ ‎(3)在(2)的条件下，若在抛物线和x轴所围成的封闭图形内画出一个最大的正方形，使得正方形的一边在x轴上，其对边的两个端点在抛物线上，试求出这个最大正方形的边长．‎ ‎24．在△ABC中，AC＝BC，∠ACB＝90°，点D为AC的中点．‎ ‎(1)如图1，E为线段DC上任意一点，将线段DE绕点D逆时针旋转90°得到线段DF，连结CF，过点F作FH⊥FC，交直线AB于点H．判断FH与FC的数量关系并加以证明．‎ ‎(2)如图2，若E为线段DC的延长线上任意一点，(1)中的其他条件不变，你在(1)中得出的结论是否发生改变，直接写出你的结论，不必证明．‎ A A B B D E C F H D C E F H 图1 图2‎ ‎25．如图，直线l1：y＝kx＋b平行于直线y＝x－1，且与直线l2：y＝mx＋交于P(－1，0)．‎ ‎(1)求直线l1、l2的解析式；‎ ‎(2)直线l1与y轴交于点A．一动点C从点A出发，先沿平行于x轴的方向运动，到达直线l2上的点B1处后，改为垂直于x轴的方向运动，到达直线l1上的点A1处后，再沿平行于x轴的方向运动，到达直线l2上的点B2处后，又改为垂直于x 轴的方向运动，到达直线l1上的点A2处后，仍沿平行于x轴的方向运动，…照此规律运动，动点C依次经过点B1，A1，B2，A2，B3，A3，…，Bn，An，…‎ ‎①求点B1，B2，A1，A2的坐标；‎ A O P x y l1‎ l2‎ A1‎ A2‎ B1‎ B2‎ B3‎ ‎②请你通过归纳得出点An、Bn的坐标；并求当动点C到达An处时，运动的总路径的长．‎ ‎2010年顺义区高中招生考试数学试题答案 一、选择题(本题共32分，每小题4分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 B A D C B C D B 二、填空题(本题共16分，每小题4分)‎ 题 号[‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 ‎，，‎ 三、解答题：(本题共30分，每小题5分)‎ ‎13．解：‎ ‎ ……………………………………………………… 4分 ‎ ………………………………………………………………… 5分 ‎14．解：‎ ‎ ①+②，得 ．‎ ‎ ． …………………………………………………… 2分 ‎ 把代入①，得 ‎ ．‎ ‎ ． ………………………………………………… 4分 ‎ ∴原方程组的解为 …………………………………………… 5分 ‎15．证明：∵ AB＝AC，点D是BC的中点，‎ ‎∴ ∠ADB＝90°． ………………… 1分[来源:学科网]‎ ‎∵ AE⊥AB，‎ ‎∴ ∠E＝90°＝∠ADB． ………………… 2分 ‎∵ AB平分，‎ ‎∴ ∠1＝∠2．……………………………… 3分 在△ADB和△AEB中，‎ ‎∴ △ADB≌△AEB．……………………………………………………… 4分 ‎∴ AD＝AE．………………………………………………………………… 5分 ‎16．解：‎ ‎ …………………………………………………… 2分 ‎ ………………………………………………………… 3分 ‎ ……………………………………………………………………… 4分 ‎ 当，时，原式＝． ………… 5分 ‎17．解：(1)∵点A 在正比例函数的图象上，‎ ‎∴ ．‎ 解得 ．‎ ‎∴ 正比例函数的解析式为 ． ……………………………… 1分 ‎∵点A 在反比例函数的图象上，‎ ‎∴ ．‎ 解得 ．‎ ‎∴ 反比例函数的解析式为．…… 2分 ‎(2)点B的坐标为， …………… 3分 不等式的解集为或． ………………………… 5分[来]‎ ‎18．解：(1)设去了x个成人，则去了(12- x)个学生，依题意，得 ‎ ……………………………………………… 2分 ‎ 解得 ． ………………………………………………………… 3分[来 ‎ ．‎ ‎ 答：小明他们一共去了8个成人，4个学生． ……………………… 4分 ‎ (2)若按团体票购票：．‎ ‎ ∵， ∴按团体票购票更省钱． ……………………… 5分 四、解答题(本题共20分，第19题6分，第20题5分，第21题5分，第22题4分)‎ ‎19．解：(1)，‎ ‎∴这1000名小学生患近视的百分比为38%． ……………………… 2分 ‎(2)抽查的中学生近视人数：263+260+37＝560，‎ ‎560÷56%＝1000(人)，‎ ‎∴本次抽查的中学生有1000人． …………………………………… 4分 ‎(3)∵8×＝2.08(万人)，‎ ‎∴该市中学生患“中度近视”的约有2.08万人． …………………… 5分 ‎∵10×＝1.04(万人)，‎ ‎∴该市小学生患“中度近视”的约有1.04万人． …………………… 6分 ‎20．解：过点A作AE⊥BD，垂足为E．‎ ‎∵BD⊥DC，∠C＝60°，BC＝6，‎ ‎∴∠1＝30°，． …………………… 1分 ‎∵AD//BC，‎ ‎∴∠2＝∠1＝30°．‎ ‎∵AE⊥BD，AD＝4，‎ ‎∴，． ……… 3分 ‎∴． ………………………………… 4分 ‎∴． …………………………………………… 5分[来源:学|科|网]‎ ‎21．(1)证明：∵AB是⊙O的直径，‎ ‎∴∠ACB＝90°． …………………………………………………… 1分 ‎∵四边形OBCD是菱形，‎ ‎∴OD//BC．‎ ‎∴∠1＝∠ACB＝90°．‎ ‎∵EF∥AC，‎ ‎∴∠2＝∠1 ＝90°． …………… 2分 ‎∵OD是半径，‎ ‎∴EF是⊙O的切线． ………………………………………… 3分 ‎(2)解：连结OC，‎ ‎∵直径AB＝4，‎ ‎∴半径OB＝OC＝2．‎ ‎∵四边形OBCD是菱形，‎ ‎∴OD＝BC＝OB＝OC＝2． ………………………………………… 4分 ‎∴∠B＝60°．‎ ‎∵OD//BC，‎ ‎∴∠EOD＝∠B＝ 60°．‎ 在Rt△EOD中，．…… 5分 ‎22．解：(1)与相似的三角形是． ……………………………… 1分 证明：∵四边形ABCD是正方形，‎ ‎∴∠A＝∠C＝∠D＝90°．‎ 由折叠知 ∠EPQ＝∠A＝90°．‎ ‎∴∠1+∠3＝90°，∠1+∠2＝90°．‎ ‎∴∠2＝∠3．‎ ‎∴∽． ……… 2分 ‎(2)设ED＝x，则AE＝，‎ 由折叠可知：EP＝AE＝．‎ ‎∵点P是CD中点，‎ ‎∴DP＝1．‎ ‎∵∠D＝90°，‎ ‎∴，‎ 即 解得 ．‎ ‎∴． ………………………………………………………… 3分 ‎∵∽，‎ ‎∴．‎ ‎∴与周长的比为4∶3． ………………………… 4分 五、解答题(本题共22分，第23题7分，第24题7分，第25题8分)‎ ‎23．解：(1)，‎ 依题意，得 ‎ ‎∴的取值范围是且． ① …………………………… 2分[来源:学#科#网Z#X#X#K]‎ ‎(2)解方程，得 ‎． …………………………………………………………… 3分 ‎∵方程的解是负数，‎ ‎∴． ∴． ② ……………………………… 4分 综合①②，及为整数，可得 ．‎ ‎∴抛物线解析式为 ． ……………………………… 5分 ‎(3)如图，设最大正方形ABCD的边长为m，则B、C两点的纵坐标为，‎ 且由对称性可知：B、C两点关于抛物线对称轴对称．‎ ‎∵抛物线的对称轴为：．‎ ‎∴点C的坐标为． ……………… 6分 ‎∵C点在抛物线上，‎ ‎∴．‎ 整理，得 ．‎ ‎∴(舍负)‎ ‎∴． …………………… 7分 ‎24．解：(1)FH与FC的数量关系是：． … 1分 证明：延长交于点G，‎ 由题意，知 ∠EDF＝∠ACB＝90°，DE＝DF．‎ ‎∴DG∥CB．‎ ‎∵点D为AC的中点，‎ ‎∴点G为AB的中点，且．‎ ‎∴DG为的中位线．‎ ‎∴．‎ ‎∵AC＝BC，‎ ‎∴DC＝DG．‎ ‎∴DC- DE ＝DG- DF．‎ 即EC ＝FG． …………………………………………………………… 2分 ‎∵∠EDF ＝90°，，‎ ‎∴∠1+∠CFD ＝90°，∠2+∠CFD＝90°．‎ ‎∴∠1 ＝∠2． …………………………………………………………… 3分 ‎∵与都是等腰直角三角形，‎ ‎∴∠DEF ＝∠DGA ＝ 45°．‎ ‎∴∠CEF ＝∠FGH ＝ 135°． …………………………………………… 4分 ‎∴△CEF ≌△FGH． ……………………………………………………… 5分 ‎∴ CF＝FH． ……………………………………………………………… 6分 ‎(2)FH与FC仍然相等． ……………………………………………… 7分 ‎25．解：(1)由题意，得 解得 ‎ ‎∴直线的解析式为 ． ………………………………… 1分 ‎∵点在直线上，‎ ‎∴．‎ ‎∴．‎ ‎∴直线的解析式为 ． ……………………………… 2分 ‎(2)① A点坐标为 (0，1)，‎ 则点的纵坐标为1，设，‎ ‎∴．‎ ‎∴．‎ ‎∴点的坐标为 ． ………………………………………… 3分[来源:学§科§网]‎ 则点的横坐标为1，设 ‎∴．‎ ‎∴点的坐标为 ． ………………………………………… 4分 同理，可得 ，． ……………………………… 6分 ‎②经过归纳得 ，． ……………… 7分 当动点到达处时，运动的总路径的长为点的横纵坐标之和再减去1，‎ 即 ． ……………………………………… 8分