扬州市2013年中考数学卷

扬州市2013年中考数学卷

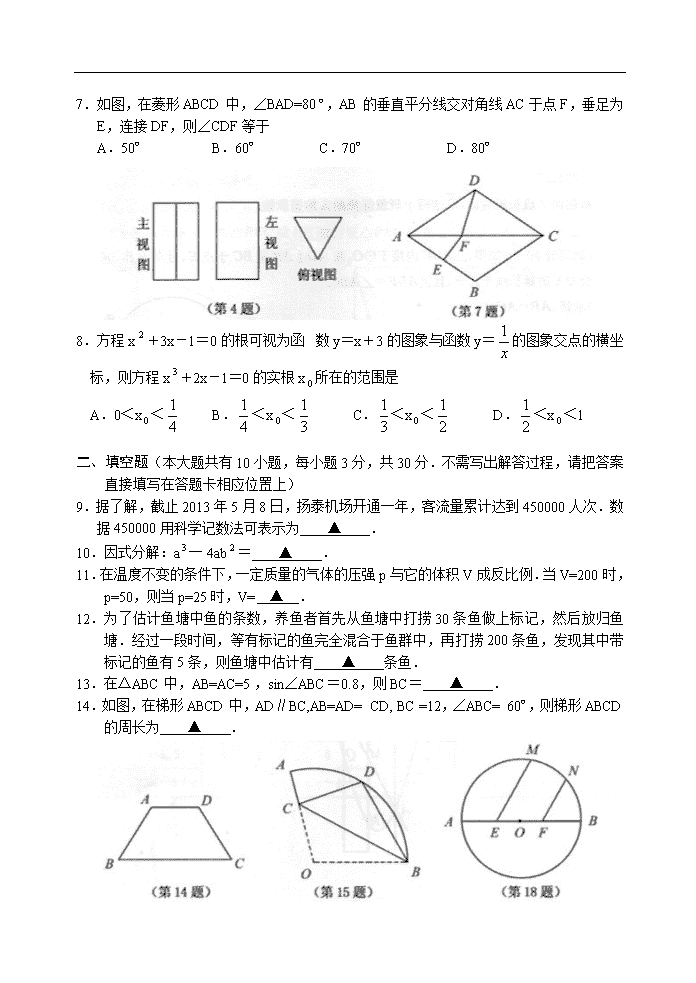
扬州市2013年初中毕业、升学统一考试数学试题 说明：‎ ‎1．本试卷共6页，包含选择题（第1题一第8题，共8题）、非选择题（第9题一第28题，共20题）两部分。本卷满分150分，考试时间为120分钟。考试结束后，请将本试卷和答题卡一并交回。‎ ‎2．答题前，考生务必将自己的姓名、准考证号填写在答题卡相应的位置上，同时务必在试卷的装订线内将本人的姓名、准考证号、毕业学校填写好，在试卷第一面的右下角写好座位号。‎ ‎3．所有的试题都必须在专用的“答题卡”上作答，选择题用2B铅笔作答、非选择题在指定位置用0.5毫米的黑色笔作答。在试卷或草稿纸上答题无效。‎ ‎4．如有作图需要，请用2B铅笔作答，并请加黑加粗，描写清楚。‎ 一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）‎ ‎１．－2的倒数是 A．－ 　　B． C．－2 D．2‎ ‎2．下列运算中，结果是a的是 ‎ A．a·a 　B．a÷a C．(a)　　　　D．（一a)‎ ‎3．下列说法正确的是 ‎ A．“明天降雨的概率是80％”表示明天有80％的时间都在降雨 B．“抛一枚硬币正面朝上的概率为”表示每抛两次就有一次正面朝上 ‎ C．“彩票中奖的概率为1％”表示买100张彩票肯定会中奖 D．“抛一枚均匀的正方体般子，朝上的点数是2的概率”，表示随着抛掷次数的增加，“抛出朝上的点数是2”这一事件发生的频率稳定在附近 ‎4．某几何体的三视图如图所示，则这个几何体是 ‎ A．三棱柱　　　　B．圆柱　　　　C．正方体　　　D．三棱锥 ‎5．下列图形中，由AB∥CD能得到∠1=∠2的是 ‎ 6．一个多边形的每个内角均为108º，则这个多边形是 ‎ A．七边形 B．六边形 C．五边形 D．四边形 ‎7．如图，在菱形ABCD中，∠BAD=80º，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF等于 ‎ A．50º B．60º C．70º D．80º ‎8．方程x＋3x－1＝0的根可视为函数y＝x＋3的图象与函数y＝的图象交点的横坐标，则方程x＋2x－1＝0的实根x所在的范围是 ‎ A．0＜x＜　 　B．＜x＜　　 C．＜x＜　　　D．＜x＜1‎ 二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．据了解，截止‎2013年5月8日，扬泰机场开通一年，客流量累计达到450000人次．数据450000用科学记数法可表示为　　▲　　．‎ ‎10．因式分解：a一4ab＝　　▲　　．‎ ‎11．在温度不变的条件下，一定质量的气体的压强p与它的体积V成反比例．当V=200时，p=50，则当p=25时，V=　▲　．‎ ‎12．为了估计鱼塘中鱼的条数，养鱼者首先从鱼塘中打捞30条鱼做上标记，然后放归鱼塘．经过一段时间，等有标记的鱼完全混合于鱼群中，再打捞200条鱼，发现其中带标记的鱼有5条，则鱼塘中估计有　　▲　　条鱼．‎ ‎13．在△ABC中，AB=AC=5，sin∠ABC＝0.8，则BC＝　　▲　　．‎ ‎14．如图，在梯形ABCD中，AD∥BC,AB=AD= CD, BC =12，∠ABC= 60º，则梯形ABCD的周长为　　▲　　．‎ ‎15．如图，在扇形OAB中，∠AOB＝110º，半径OA＝18，将扇形OAB沿过点B的直线折叠，点O恰好落在上的点D处，折痕交OA于点C，则的长为　　▲　　．‎ ‎16．已知关子x的方程＝2的解是负数，则n的取值范围为　　▲　　．‎ ‎17．矩形的两邻边长的差为2，对角线长为4，则矩形的面积为　　▲　　．‎ ‎18．如图，已知⊙O的直径AB＝6，E、F为AB的三等分点，从M、N为上两点，且∠MEB＝∠NFB= 60º，则EM＋FN＝　　▲　　．‎ 三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19.（本题满分8分）‎ ‎ (1）计算：()一2sin60º＋；‎ ‎(2）先化简，再求值：(x＋l)(2x－1)一(x－3)，其中x＝一2.‎ ‎ ‎ ‎20．（本题满分8分）已知关于x、y的方程组 的解满足x＞0, y＞0,求实数a的取值范围．‎ ‎21.（本题满分8分）端午节期间，扬州一某商场为了吸引顾客，开展有奖促销活动，设立了一个可以自由转动的转盘，转盘被分成4个面积相等的扇形，四个扇形区域里分别标有“10元”、“20元”、“30元”和“40元”的字样（如图）．规定：同一日内，顾客在本商场每消费满100元，就可以转转盘一次，商场根据转盘指针指向区域所标金额返还相应数额的购物券．某顾客当天消费240元，转了两次转盘．‎ ‎ (1）该顾客最少可得　　▲　　元购物券，最多可得　　▲　　元购物券；‎ ‎（2）请用画树状图或列表的方法，求该顾客所获购物券金额不低于50元的概率．‎ ‎10元 ‎20元 ‎30元 ‎40元 ‎22．（本题满分8分）为声援扬州“运河申遗”，某校举办了一次运河知识竞赛，满分10分，学生得分均为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包括9分）为优秀．这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示．‎ ‎(1）补充完成下面的成绩统计分析表：‎ 组别 平均分 中位数 方差 合格率 优秀率 甲组 ‎6.7‎ ‎▲‎ ‎3.41‎ ‎90%‎ ‎20%‎ 乙组 ‎▲‎ ‎7.5‎ ‎1.69‎ ‎80%‎ ‎10%‎ ‎ (2）小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上表可知，小明是　▲　组的学生；（填“甲”或“乙”）‎ ‎(3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你给出两条支持乙组同学观点的理由．‎ ‎23.（本题满分10分）如图，在△ABC中，∠ACB= 90º，AC＝BC，点D在边AB上，连接CD，将线段CD绕点C顺时针旋转90ºCE至“位置，连接AE．‎ ‎(1) 求证：AB⊥AE；‎ ‎(2）若BC=AD·AB，求证：四边形ADCE为正方形．‎ A B C D E ‎24.（本题满分10分）某校九(1)、九(2)两班的班长交流了为四川雅安地震灾区捐款的情况：‎ ‎（Ⅰ）九（1)班班长说：“我们班捐款总额为1200元，我们班人数比你们班多8人．”‎ ‎（Ⅱ）九（2)班班长说：“我们班捐款总额也为1200元，我们班人均捐款比你们班人均捐款多20%．”‎ 请根据两个班长的对话，求这两个班级每班的人均捐款数．‎ ‎25．（本题满分10分）如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF＝∠ABC．‎ ‎(1）求证：AB＝AC；‎ ‎(2)若AD＝4, cos∠ABF＝，求DE的长．‎ ‎26.（本题满分10分）如图，抛物线y＝x－2x－8交y轴于点A，交x轴正半轴于点B．‎ ‎ (1)求直线AB对应的函数关系式；‎ ‎(2)有一宽度为1的直尺平行于y轴，在点A、B之间平行移动，直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ．设M点的横坐标为m，且0＜m＜3．试比较线段ＭＮ与PQ的大小．‎ ‎27.（本题满分12分）如图1，在梯形ABCD中，AB∥CD，∠B＝90º，AB＝2，CD＝1，BC＝m，P为线段BC上的一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E．设BP＝x，CE＝y．‎ ‎(1)求y与x的函数关系式；‎ ‎(2)若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围．‎ ‎(3)如图2，若m＝4，将△PEC沿PE翻折至△PEG位置，∠BAG= 90º，求BP长．‎ ‎28.（本题满分12分）如果10＝n，那么称b为n的劳格数，记为b＝d (n)，由定义可知：10＝n与b＝d (n)所表示的是b、n两个量之间的同一关系．‎ ‎ (1)根据劳格数的定义，填空：d(10)＝　▲　 ，d(10)＝　▲　 ；‎ ‎ (2）劳格数有如下运算性质：‎ ‎ 若m、,n为正数，则d(mn) ＝d(m)＋d(n)，d(n)＝d(m）一d(n)．‎ 根据运算性质，填空：‎ ‎ ＝　 ▲ 　(a为正数），‎ ‎ 若d(2) ＝0.3010，则d(4) ＝　▲　，d(5）＝　▲　，d(0. 08) ＝　▲　；‎ ‎ (3）下表中与数x对应的劳格数d (x)有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．‎ x ‎1.5‎ ‎3‎ ‎5‎ ‎6‎ ‎8‎ ‎9‎ ‎12‎ ‎27‎ d(x)‎ ‎3a－b＋c ‎2a－b a＋c ‎1＋a－b－c ‎3－3a－3c ‎4a－2b ‎3－b－2c ‎6a－3b 扬州市2013年初中毕业、升学统一考试数学试题 参考答案及评分建议 说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神酌情给分．‎ 一、选择题（本大题共有8小题，每小题3分，共24分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 选项 A D D A B C B C 二、填空题（本大题共有10小题，每小题3分，共30分）‎ ‎9．4.5×10 10．a (a十2b) (a一2b) 11．400 12．1200 　　13．6‎ ‎14．30 15．5π 16．n＜2且n≠ 17．6 18．‎ 三、解答题（本大题共有10小题，共96分．解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．解：(1)原式＝4一＋2，……………………………………………… 3分 ‎ ＝4＋． …………………………………………………………4分 ‎ （2）原式＝x＋7ｘ一10 …………………………………………… 3分 ‎ ∴当x＝一2时，原式＝一20． …………………………………4分 ‎＞‎ ‎＞‎ ‎20．解：解方程组得（每个解２分）…………………………………4分 ‎ 　　由题意得 …………………………………………5分 解不等式组得一＜a＜2（解一个不等式1分）…………………………7分 ‎ ∴a的取值范围为一＜a＜2 …………………………………………8分 ‎21．解：(1) 20 ， 80 ；………………………………………………………… 2分 ‎ (2) 解法一：用树状图分析如下：‎ 开 始 ‎40‎ ‎20‎ ‎30‎ ‎10‎ ‎40‎ ‎20‎ ‎30‎ ‎10‎ ‎40‎ ‎20‎ ‎30‎ ‎10‎ ‎40‎ ‎20‎ ‎30‎ ‎10‎ ‎40‎ ‎20‎ ‎30‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎50‎ ‎60‎ ‎70‎ ‎80‎ 第一次 第二次 结果 ‎10‎ 解法二：用列表法分析如下：‎ 第二次 第一次 ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎40‎ ‎50‎ ‎60‎ ‎70‎ ‎80‎ ‎………………………………………………………………………………………6分 ‎∴P(不低于50元）＝＝．………………………………………………… 8分 ‎22．（1） 7.1 ， 6 （每空2分）………………………………………………4分 ‎（2） 甲 ……………………………………………………………………6分 ‎（3）乙组的平均分高于甲组；乙组成绩的方差低于甲组，乙组成绩的稳定性好于甲组．‎ ‎ （答案不唯一只要合理即可）……………………………………………………8分 ‎23. (1)证明：∵∠BCA＝∠DCE＝90º，∴∠BCD＝∠ACE ‎ ∵CB＝CA，CD＝CE，∴△BCD≌△ACE，∴∠CAE＝∠CBD ……3分 ‎ ∵AC＝BC，∠ACB＝90º，∴∠ABC＝∠BAC=45º，∴∠CAE=45º ‎ ∴∠BAE＝90º，∴ AB⊥AE ……………………………………… 5分 ‎(2）证明：∵BC＝AD·AB，BC＝AC，∴ AC＝AD·AB，∴＝‎ ‎ ∴∠CAD＝∠BAC，∴△CAD≌△BAC，‎ ‎∴∠ADC＝∠ACB=90º ………………………………………………8分 ‎ ∴∠DCE＝∠DAE＝90º，∴四边形ADCE是矩形 ………………9分 ‎ ∵CD ＝CE，∴四边形ADCE是正方形 …………………………10分 ‎24．解法一：设九（1)班有x人，则九（(2）班人数为（(x－8)人，由题意，得 ‎ (1+20％）＝ ………………………………………………4分 ‎ 解得x＝48 ………………………………………………………………7分 ‎ 经检验，x=48是原程的解． ………………………………………… 8分 ‎ 所以x－8＝40．＝25（元），＝30(元） ………………9分 ‎ 答：九（(1）班人均捐款为25元，九（2)班人均捐款为30元．……10分 解法二：设九（1)班人均捐款y元，则九（2）班人均捐款（1十20％)y元，‎ ‎ 由题意，－8＝　……………………………………4分 ‎ 解得y＝25 ……………………………………………………………… 7分 ‎ 经检验，y=25是原程的解． ……………………………………………8分 ‎ 当y＝25时，（1＋20%)y＝30（元） ……………………………………9分 ‎ 答：九（1)班人均捐款为25元，九（2)班人均捐款为30元． …… 10分 ‎25． （1）证明：连接BD，由AD⊥AB可知BD必过点O ‎ ∴BF相切于⊙O，∴∠ABD十∠ABF＝90º ‎ ∵AD⊥AB，∴∠ABD＋∠ADB＝90º，∴∠ABF＝∠ADB …………3分 ‎ ∵∠ABC＝∠ABF，∴∠ABC＝∠ADB ‎ 又∠ACB＝∠ADB，∴∠ABC＝＝∠ACB，∴AB＝AC ………………5分 ‎ （2）在Rt△ABD中，∠BAD＝90º ‎ cos∠ADB＝，∴BD＝ ＝＝＝5 ……6分 ‎ ∴AB＝3 ……………………………………………………………………7分 ‎ 在Rt△ABE中，∠BAE=90º ‎ Cos∠ABE＝，∴BE＝＝＝‎ ‎ ∴AE＝＝ …………………………………………………9分 ‎ ∴DE＝AD－AE＝4－＝…………………………………………… 10分 ‎26．解：(1）点A坐标（(0，一8)，点B坐标（4，0)………………………………2分 ‎ 设直线AB函数解析式为y＝kx＋b，将A、B点坐标代人得k =2，b＝一8‎ ‎ 所以直线AB的解析式为y＝2x－8…………………………………………5分 ‎ (2）由题意知M点坐标为（m，2m－8) ，N点坐标为（m，m－2m－8)，‎ 且0＜m＜3‎ ‎ 所以MN＝(2m－8)一（m－2m－8) ＝－m＋4m ……………………６分 ‎ 同理可得PQ＝－（m＋1)十4(m＋1) ＝－m十2m＋3 ………………7分 ‎ ①当PQ＞MN时，－m十2m＋3＞－m＋4m，解得m＜‎ ‎ ∴0＜m＜时，PQ＞MN ………………………………………………8分 ‎ ②当PQ＝MN时，－m十2m＋3＝－m＋4m，解得m＝‎ ‎∴m＝时，PQ＝MN；…………………………………………………9分 ‎ ③当PQ＜MN时，－m十2m＋3＜－m＋4m，解得m＞‎ ‎ ∴当＜m＜3 时PQ＜MN．…………………………………………10分 ‎ 注：写m的取值范围时未考虑0＜m＜3条件的统一扣1分．‎ ‎27．解：(1) ∵AB∥CD，∠B.=90º，∴∠B＝∠C＝90º，∴∠APB＋∠BAP＝90º ‎ ∵PE⊥PA，∴∠APE＝90º，∴∠APB＋∠CPE＝90º，∴∠BAP＝∠CPE ‎ 在△ABP和△PCE中，∠B＝∠C＝90º，∠BAP ＝∠CPE，‎ ‎ ∴△ABP∽△PCE …………………………………………………………2分 ‎ ∴＝，∵BC＝m，BP＝x，∴PC＝m一x ‎ ∴＝，∴y＝x＋x ……………………………………４分 ‎ ∴y与x的函数关系式为y＝x＋x，x的取值范围为。0＜x＜m．‎ ‎ (2) ∵y＝x＋x＝(x－)＋‎ ‎ ∴当x＝时，y＝ ………………………………………………6分 ‎ ∴点E总在县段CD上，∴≤1．∴m≤2，∴0＜m＜2………8分 ‎ 注：写m的取值范围时未交待m＞0不扣分．‎ ‎ (3）连接CG，过P作PH⊥AG于H．‎ ‎ 由翻折可知CG⊥PE，PG＝PC＝4－x，又∵PE⊥PA，∴CG∥PA ‎ 又∵∠B＝∠BAG＝90º，∴AG∥PC，四边形APCG为平行四边形……9分 ‎ ∴AG＝PC＝4一x ‎ ∵∠B＝∠BAG＝∠AHP＝90º，∴四边形ABPH为矩形 ‎ ∴AH＝BP＝x，PH＝AB＝2，∴HG＝4－2x …………………………10分 ‎ 在Rt△PHG中，∵PH＋HG＝PG，∴2＋(4－2x)＝(4－x)‎ ‎ 解得x＝2，x＝，∴BP＝2或 ……………………………………12分 ‎28． (1 )　1，－2（每空1分） ……………………………………………………………2分 ‎ (2)　3，0.6020，0. 6990，－1.097（每空1分）……………………………………6分 ‎ (3）若d（3）≠2a－b，则d（9）＝2d（3）≠ 4a－2b，‎ ‎ 　 D（27）＝3d（3）≠6a－3b ‎ 从而表中有三个劳格数是错误的，与题设矛盾 ‎ ∴d(3)＝2a－b ……………………………………………………………………8分 ‎ 若d.(5) ≠a＋c，则d(2) ＝1－d(5) ≠1－a－c ‎ ∴d(8)＝3d(2) ≠3－3a－3c ‎ d(6) ＝d(3) ＋d(2) ≠1＋a－b－c ‎ 表中也有三个劳格数是错误的，与题设矛盾 ‎ ∴d（5）＝a＋c …………………………………………………………………10分 ‎ ∴表中只有d（1.5）和d（12）的值是错误的，应纠正为：‎ ‎ D（1.5）＝d（3）＋d（5）－1＝3a－b＋c－1 …………………………11分 ‎ D（12）＝d（3）＋2d（2）＝2－b－2c ………………………………12分 ‎ 注：如果仅指出错误的劳格数，未说明理由，则每指出1个给1分．‎