- 2021-05-10 发布 |
- 37.5 KB |
- 107页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三年中考20102012全国各地中考数学试题分类汇编汇编与圆有关的解答题
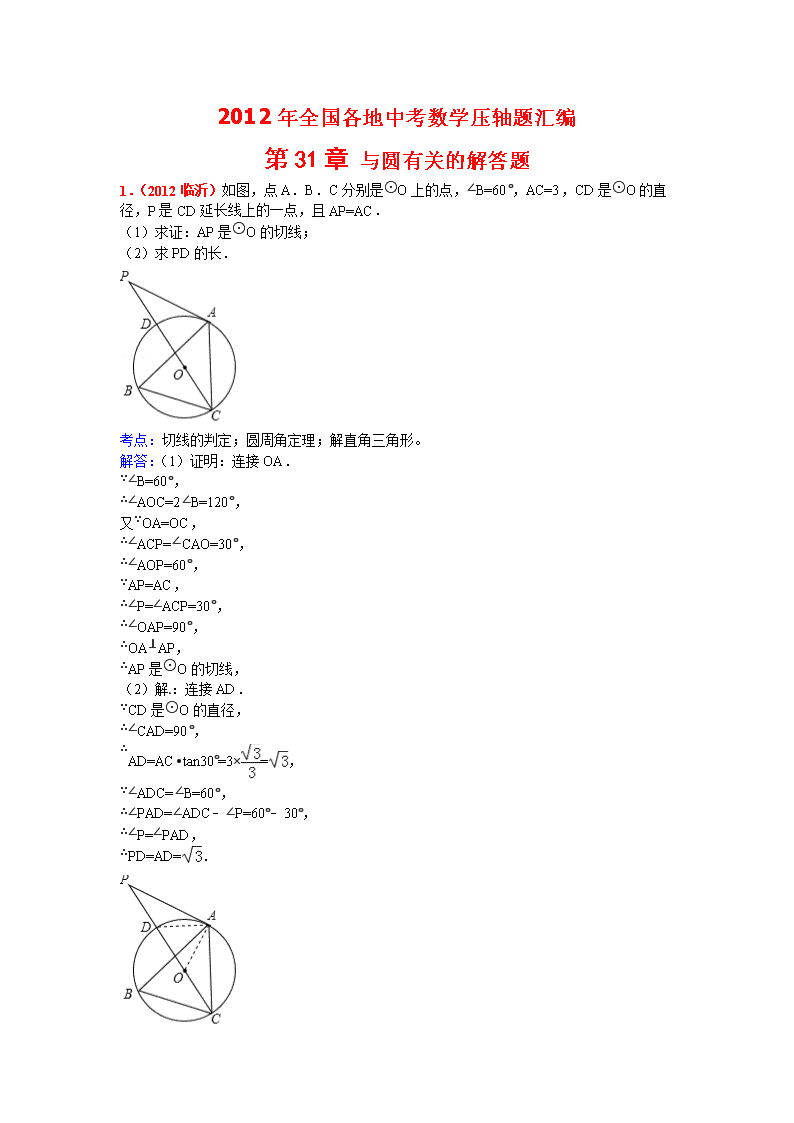
2012年全国各地中考数学压轴题汇编 第31章 与圆有关的解答题 1.(2012临沂)如图,点A.B.C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC. (1)求证:AP是⊙O的切线; (2)求PD的长. 考点:切线的判定;圆周角定理;解直角三角形。 解答:(1)证明:连接OA. ∵∠B=60°, ∴∠AOC=2∠B=120°, 又∵OA=OC, ∴∠ACP=∠CAO=30°, ∴∠AOP=60°, ∵AP=AC, ∴∠P=∠ACP=30°, ∴∠OAP=90°, ∴OA⊥AP, ∴AP是⊙O的切线, (2)解:连接AD. ∵CD是⊙O的直径, ∴∠CAD=90°, ∴AD=AC•tan30°=3×=, ∵∠ADC=∠B=60°, ∴∠PAD=∠ADC﹣∠P=60°﹣30°, ∴∠P=∠PAD, ∴PD=AD=. 2.(2012义乌市)如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°. (1)求∠ABC的度数; (2)求证:AE是⊙O的切线; (3)当BC=4时,求劣弧AC的长. 考点:切线的判定;圆周角定理;弧长的计算。 解答:解:(1)∵∠ABC与∠D都是弧AC所对的圆周角, ∴∠ABC=∠D=60°; (2)∵AB是⊙O的直径, ∴∠ACB=90°. ∴∠BAC=30°, ∴∠BAE=∠BAC+∠EAC=30°+60°=90°, 即BA⊥AE, ∴AE是⊙O的切线; (3)如图,连接OC, ∵OB=OC,∠ABC=60°, ∴△OBC是等边三角形, ∴OB=BC=4,∠BOC=60°, ∴∠AOC=120°, ∴劣弧AC的长为. 3.(2012•杭州)如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3,MN=2. (1)求∠COB的度数; (2)求⊙O的半径R; (3)点F在⊙O上(是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比. 考点: 切线的性质;含30度角的直角三角形;勾股定理;垂径定理;平移的性质;旋转的性质;相似三角形的判定与性质。 专题: 计算题。 分析: (1)由AE与圆O相切,根据切线的性质得到AE与CE垂直,又OB与AT垂直,可得出两直角相等,再由一对对顶角相等,利用两对对应角相等的两三角形相似可得出三角形AEC与三角形OBC相似,根据相似三角形的对应角相等可得出所求的角与∠A相等,由∠A的度数即可求出所求角的度数; (2)在直角三角形AEC中,由AE及tanA的值,利用锐角三角函数定义求出CE的长,再由OB垂直于MN,由垂径定理得到B为MN的中点,根据MN的长求出MB的长,在直角三角形OBM中,由半径OM=R,及MB的长,利用勾股定理表示出OB的长,在直角三角形OBC中,由表示出OB及cos30°的值,利用锐角三角函数定义表示出OC,用OE﹣OC=EC列出关于R的方程,求出方程的解得到半径R的值; (3)把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有6个,如图所示,每小图2个,顶点在圆上的三角形,延长EO与圆交于点D,连接DF,由第二问求出半径,的长直径ED的长,根据ED为直径,利用直径所对的圆周角为直角,得到三角形EFD为直角三角形,由∠FDE为30°,利用锐角三角函数定义求出DF的长,表示出三角形EFD的周长,再由第二问求出的三角形OBC的三边表示出三角形BOC的周长,即可求出两三角形的周长之比. 解答: 解:(1)∵AE切⊙O于点E, ∴AE⊥CE,又OB⊥AT, ∴∠AEC=∠CBO=90°, 又∠BCO=∠ACE, ∴△AEC∽△OBC,又∠A=30°, ∴∠COB=∠A=30°; (2)∵AE=3,∠A=30°, ∴在Rt△AEC中,tanA=tan30°=,即EC=AEtan30°=3, ∵OB⊥MN,∴B为MN的中点,又MN=2, ∴MB=MN=, 连接OM,在△MOB中,OM=R,MB=, ∴OB==, 在△COB中,∠BOC=30°, ∵cos∠BOC=cos30°==, ∴BO=OC, ∴OC=OB=, 又OC+EC=OM=R, ∴R=+3, 整理得:R2+18R﹣115=0,即(R+23)(R﹣5)=0, 解得:R=﹣23(舍去)或R=5, 则R=5; (3)在EF同一侧,△COB经过平移、旋转和相似变换后,这样的三角形有6个, 如图,每小图2个,顶点在圆上的三角形,如图所示: 延长EO交圆O于点D,连接DF,如图所示, ∵EF=5,直径ED=10,可得出∠FDE=30°, ∴FD=5, 则C△EFD=5+10+5=15+5, 由(2)可得C△COB=3+, ∴C△EFD:C△COB=(15+5):(3+)=5:1. 点评: 此题考查了切线的性质,垂径定理,勾股定理,相似三角形的判定与性质,含30°直角三角形的性质,平移及旋转的性质,以及锐角三角函数定义,熟练掌握定理及性质是解本题的关键. 4.(2012•烟台)如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE. (1)求证:CF是⊙O的切线; (2)若sin∠BAC=,求的值. 考点: 切线的判定;圆周角定理;相似三角形的判定与性质。 分析: (1)首先连接OC,由CD⊥AB,CF⊥AF,CF=CE,即可判定AC平分∠BAF,由圆周角定理即可得∠BOC=2∠BAC,则可证得∠BOC=∠BAF,即可判定OC∥AF,即可证得CF是⊙O的切线; (2)由垂径定理可得CE=DE,即可得S△CBD=2S△CEB,由△ABC∽△CBE,根据相似三角形的面积比等于相似比的平方,易求得△CBE与△ABC的面积比,继而可求得的值. 解答: (1)证明:连接OC. ∵CE⊥AB,CF⊥AF,CE=CF, ∴AC平分∠BAF,即∠BAF=2∠BAC. ∵∠BOC=2∠BAC, ∴∠BOC=∠BAF. ∴OC∥AF. ∴CF⊥OC. ∴CF是⊙O的切线. (2)解:∵AB是⊙O的直径,CD⊥AB, ∴CE=ED,∠ACB=∠BEC=90°. ∴S△CBD=2S△CEB,∠BAC=∠BCE, ∴△ABC∽△CBE. ∴==(sin∠BAC)2==. ∴=. 点评: 此题考查了切线的判定、垂径定理、相似三角形的判定与性质以及圆周角定理等知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用. 5.(2012•梅州)如图,AC是⊙O的直径,弦BD交AC于点E. (1)求证:△ADE∽△BCE; (2)如果AD2=AE•AC,求证:CD=CB. 考点: 圆周角定理;相似三角形的判定与性质。 专题: 证明题。 分析: (1)由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠B,又由对顶角相等,可证得:△ADE∽△BCE; (2)由AD2=AE•AC,可得,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,以求得AC⊥BD,由垂径定理即可证得CD=CB. 解答: (1)证明:如图∵∠A与∠B是对的圆周角, ∴∠A=∠B, 又∵∠1=∠2, ∴△ADE∽△BCE; (2)证明:如图, ∵AD2=AE•AC, ∴, 又∵∠A=∠A, ∴△ADE∽△ACD, ∴∠AED=∠ADC, 又∵AC是⊙O的直径, ∴∠ADC=90°, 即∠AED=90°, ∴直径AC⊥BD, ∴CD=CB. 点评: 此题考查了圆周角定理、垂径定理一相似三角形的判定与性质.此题难度不大,注意数形结合思想的应用. 6.(2012•扬州)如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D. (1)求证:AC平分BAD; (2)若AC=2,CD=2,求⊙O的直径. 考点: 切线的性质;角平分线的性质;勾股定理;相似三角形的判定与性质。 专题: 计算题。 分析: (1)连接OC,根据切线的性质判断出AD∥OC,得到∠DAC=∠OCA,再根据OA=OC得到∠OAC=∠OCA, 可得AC平分∠BAD. (2)连接BC,得到△ADC∽△ACB,根据相似三角形的性质即可求出AB的长. 解答: 解:(1)如图:连接OC, ∵DC切⊙O于C, ∴AD⊥CD, ∴∠ADC=∠OCF=90°, ∴AD∥OC, ∴∠DAC=∠OCA, ∵OA=OC, ∴∠OAC=∠OCA, 即AC平分∠BAD. (2)连接BC. ∵AB是直径, ∴∠ACB=90°=∠ADC, ∵∠OAC=∠OCA, ∴△ADC∽△ACB, ∴, 在Rt△ADC中,AC=2,CD=2, ∴AD=4, ∴, ∴AB=5. 点评: 本题考查了切线的性质、角平分线的性质、勾股定理、相似三角形的判定与性质,是一道综合性较强的题目,作出相应辅助线是解题的关键. 7.(2012年中考)如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°. (1)求∠B的大小; (2)已知AD=6求圆心O到BD的距离. 8.(2012•资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP. (1)BD=DC吗?说明理由; (2)求∠BOP的度数; (3)求证:CP是⊙O的切线; 如果你解答这个问题有困难,可以参考如下信息: 为了解答这个问题,小明和小强做了认真的探究,然后分别用不同的思路完成了这个题目.在进行小组交流的时候,小明说:“设OP交AC于点G,证△AOG∽△CPG”;小强说:“过点C作CH⊥AB于点H,证四边形CHOP是矩形”. 考点: 切线的判定;等腰三角形的性质;圆周角定理。 专题: 探究型。 分析: (1)连接AD,由圆周角定理可知∠ADB=90°,再由AB=AC可知△ABC是等腰三角形,故BD=DC; (2)由于AD是等腰三角形ABC底边上的中线,所以∠BAD=∠CAD,故=,进而可得出BD=DE,故BD=DE=DC, 所以∠DEC=∠DCE,△ABC中由等腰三角形的性质可得出∠ABC=75°,故∠DEC=75°由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,再由OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°; (3)设OP交AC于点G,由∠BOP=90°可知∠AOG=90°在Rt△AOG中,由∠OAG=30°,可知=,由于==,所以=,=,再根据∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性质可知∠GPC=∠AOG=90°,故可得出CP是⊙O的切线. 解答: (1)解:BD=DC. 连接AD,如图1, ∵AB是直径, ∴∠ADB=90°, ∵AB=AC, ∴BD=DC; (2)解:∵AD是等腰三角形ABC底边上的中线, ∴∠BAD=∠CAD, ∴=, ∴BD=DE, ∴BD=DE=DC, ∴∠DEC=∠DCE, ∵△ABC中,AB=AC,∠A=30° ∴∠DCE=∠ABC=(180°﹣30°)=75°, ∴∠DEC=75° ∴∠EDC=180°﹣75°﹣75°=30° ∵BP∥DE, ∴∠PBC=∠EDC=30°, ∴∠ABP=∠ABC﹣∠PBC=75°﹣30°=45° ∵OB=OP, ∴∠OBP=∠OPB=45°, ∴∠BOP=90°; (3)证明:证法一:设OP交AC于点G,则∠AOG=∠BOP=90° 在Rt△AOG中, ∵∠OAG=30°, ∴=, 又∵==, ∴=, ∴=, 又∵∠AGO=∠CGP ∴△AOG∽△CPG, ∴∠GPC=∠AOG=90°, ∴CP是⊙O的切线) 证法二:过点C作CH⊥AB于点H,如图2,则∠BOP=∠BHC=90°, ∴PO∥CH 在Rt△AHC中, ∵∠HAC=30°, ∴CH=AC, 又∵PO=AB=AC, ∴PO=CH, ∵四边形CHOP是平行四边形 ∴四边形CHOP是矩形, ∴∠OPC=90°, ∴CP是⊙O的切线. 点评: 本题考查的是切线的判定定理、等腰三角形的性质、圆周角定理及相似三角形的判定与性质,在判定圆的切线时构造直角三角形,再利用直角三角形的性质去证明过圆心的直线与切线垂直. 9.(2012•德州)如图,点A,E是半圆周上的三等分点,直径BC=2,AD⊥BC,垂足为D,连接BE交AD于F,过A作AG∥BE交BC于G. (1)判断直线AG与⊙O的位置关系,并说明理由. (2)求线段AF的长. 考点: 切线的判定;等边三角形的判定与性质;垂径定理;解直角三角形。 专题: 计算题;证明题。 分析: (1)求出弧AB=弧AE=弧EC,推出OA⊥BE,根据AG∥BE,推出OA⊥AG,根据切线的判定即可得出答案; (2)求出等边三角形AOB,求出BD、AD长,求出∠EBC=30°,在△FBD中,通过解直角三角形求出DF即可. 解答: 解:(1)直线AG与⊙O的位置关系是AG与⊙O相切, 理由是:连接OA, ∵点A,E是半圆周上的三等分点, ∴弧AB=弧AE=弧EC, ∴点A是弧BE的中点, ∴OA⊥BE, 又∵AG∥BE, ∴OA⊥AG, ∴AG与⊙O相切. (2)∵点A,E是半圆周上的三等分点, ∴∠AOB=∠AOE=∠EOC=60°, 又∵OA=OB, ∴△ABO为正三角形, 又∵AD⊥OB,OB=1, ∴BD=OD=,AD=, 又∵∠EBC=∠EOC=30°, 在Rt△FBD中,FD=BD•tan∠EBC=BD•tan30°=, ∴AF=AD﹣DF=﹣=. 答:AF的长是. 点评: 本题考查了解直角三角形,垂径定理,切线的判定等知识点的应用,能运用定理进行推理和计算是解此题的关键,注意:垂径定理和解直角三角形的巧妙运用,题目比较好,难度也适中. 10.(2012•湘潭)如图,在⊙O上位于直径AB的异侧有定点C和动点P,AC=AB,点P在半圆弧AB上运动(不与A、B两点重合),过点C作直线PB的垂线CD交PB于D点. (1)如图1,求证:△PCD∽△ABC; (2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由; (3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数. 考点: 圆周角定理;全等三角形的性质;垂径定理;相似三角形的判定。 专题: 几何综合题。 分析: (1)由AB是⊙O的直径,根据直径对的圆周角是直角,即可得∠ACB=90°,又由PD⊥CD,可得∠D=∠ACB,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠P,根据有两角对应相等的三角形相似,即可判定:△PCD∽△ABC; (2)由△PCD∽△ABC,可知当PC=AB时,△PCD≌△ABC,利用相似比等于1的相似三角形全等即可求得; (3)由∠ACB=90°,AC=AB,可求得∠ABC的度数,然后利用相似,即可得∠PCD的度数,又由垂径定理,求得=,然后利用圆周角定理求得∠ACP的度数,继而求得答案. 解答: (1)证明:∵AB是⊙O的直径, ∴∠ACB=90°, ∵PD⊥CD, ∴∠D=90°, ∴∠D=∠ACB, ∵∠A与∠P是对的圆周角, ∴∠A=∠P, ∴△PCD∽△ABC; (2)解:当PC是⊙O的直径时,△PCD≌△ABC, 理由:∵AB,PC是⊙O的半径, ∴AB=PC, ∵△PCD∽△ABC, ∴△PCD≌△ABC; (3)解:∵∠ACB=90°,AC=AB, ∴∠ABC=30°, ∵△PCD∽△ABC, ∴∠PCD=∠ABC=30°, ∵CP⊥AB,AB是⊙O的直径, ∴=, ∴∠ACP=∠ABC=30°, ∴∠BCD=∠AC﹣∠ACP﹣∠PCD=90°﹣30°﹣30°=30°. 点评: 此题考查了圆周角定理、垂径定理、相似三角形的判定与性质、全等三角形的判定与性质以及直角三角形的性质等知识.此题综合性较强,难度适中,注意数形结合思想的应用. 11.(2012•济宁)如图,AB是⊙O的直径,AC是弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P,连接PC、BC. (1)猜想:线段OD与BC有何数量和位置关系,并证明你的结论. (2)求证:PC是⊙O的切线. 考点: 切线的判定与性质;全等三角形的判定与性质;三角形中位线定理;圆周角定理。 分析: (1)根据垂径定理可以得到D是AC的中点,则OD是△ABC的中位线,根据三角形的中位线定理可以得到OD∥BC,CD=BC; (2)连接OC,设OP与⊙O交于点E,可以证得△OAP≌△OCP,利用全等三角形的对应角相等,以及切线的性质定理可以得到:∠OCP=90°,即OC⊥PC,即可等证. 解答: (1)猜想:OD∥BC,CD=BC. 证明:∵OD⊥AC, ∴AD=DC ∵AB是⊙O的直径, ∴OA=OB…2分 ∴OD是△ABC的中位线, ∴OD∥BC,OD=BC (2)证明:连接OC,设OP与⊙O交于点E. ∵OD⊥AC,OD经过圆心O, ∴,即∠AOE=∠COE 在△OAP和△OCP中, ∵OA=OC,OP=OP, ∴△OAP≌△OCP, ∴∠OCP=∠OAP ∵PA是⊙O的切线, ∴∠OAP=90°. ∴∠OCP=90°,即OC⊥PC ∴PC是⊙O的切线. 点评: 本题考查了切线的性质定理以及判定定理,三角形的中位线定理,证明圆的切线的问题常用的思路是根据切线的判定定理转化成证明垂直的问题. 12.(2012•德阳)如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G. (1)求证:AE•FD=AF•EC; (2)求证:FC=FB; (3)若FB=FE=2,求⊙O的半径r的长. 考点: 切线的判定与性质;等腰三角形的性质;等腰三角形的判定;直角三角形斜边上的中线;勾股定理;圆周角定理;相似三角形的判定与性质。 专题: 证明题;几何综合题。 分析: (1)由BD是⊙O的切线得出∠DBA=90°,推出CH∥BD,证△AEC∽△AFD,得出比例式即可; (2)证△AEC∽△AFD,△AHE∽△ABF,推出BF=DF,根据直角三角形斜边上中线性质得出CF=DF=BF即可; (3)求出EF=FC,求出∠G=∠FAG,推出AF=FG,求出AB=BG,连接OC,BC,求出∠FCB=∠CAB推出CG是⊙O切线,由切割线定理得出(2+FG)2=BG×AG=2BG2, 在Rt△BFG中,由勾股定理得出BG2=FG2﹣BF2,推出FG2﹣4FG﹣12=0,求出FG即可. 解答: (1)证明:∵BD是⊙O的切线, ∴∠DBA=90°, ∵CH⊥AB, ∴CH∥BD, ∴△AEC∽△AFD, ∴=, ∴AE•FD=AF•EC. (2)证明:∵CH∥BD, ∴△AEC∽△AFD,△AHE∽△ABF, ∴==, ∵CE=EH(E为CH中点), ∴BF=DF,[来源:www.shulihua.net数理化网] ∵AB为⊙O的直径, ∴∠ACB=∠DCB=90°, ∴CF=DF=BF, 即CF=BF. (3)解:∵BF=CF=DF(已证),EF=BF=2, ∴EF=FC, ∴∠FCE=∠FEC, ∵∠AHE=∠CHG=90°, ∴∠FAH+∠AEH=90°,∠G+∠GCH=90°, ∵∠AEH=∠CEF, ∴∠G=∠FAG, ∴AF=FG, ∵FB⊥AG, ∴AB=BG, 连接OC,BC, ∵BF切⊙O于B, ∴∠FBC=∠CAB, ∵OC=OA,CF=BF, ∴∠FCB=∠FBC,∠OCA=∠OAC, ∴∠FCB=∠CAB, ∵∠ACB=90°, ∴∠ACO+∠BCO=90°, ∴∠FCB+∠BCO=90°, 即OC⊥CG, ∴CG是⊙O切线, ∵GBA是⊙O割线, FB=FE=2,由切割线定理得:(2+FG)2=BG×AG=2BG2, 在Rt△BFG中,由勾股定理得:BG2=FG2﹣BF2, ∴FG2﹣4FG﹣12=0, 解得:FG=6,FG=﹣2(舍去), 由勾股定理得: AG=BG==4, ∴⊙O的半径是2. 点评: 本题考查了切线的性质和判定,相似三角形的性质和判定,等腰三角形的性质和判定,直角三角形斜边上中线的性质,圆周角定理,勾股定理等知识点的综合运用,题目综合性比较强,有一定的难度. A B C D E O 第20题图 13.(2012年中考)(满分12分)如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E. (1) 求证:AC平分∠DAB; (2) 若∠B=60º,CD=2,求AE的长. 在直角三角形ACD中,根据30°角所对的直角边等于斜边的一半,由CD的长求出AC的长,在直角三角形ABC中,根据cos30°及AC的长,利用锐角三角函数定义求出AB的长,进而得出半径OE的长,由∠EAO为60°,及OE=OA,得到三角形AEO为等边三角形,可得出AE=OA=OE,即可确定出AE的长; 法2:连接EC,由AB为圆O的直径,根据直径所对的圆周角为直角可得出∠ACB为直角,在直角三角形ABC中,由∠B的度数求出∠3的度数为30°,可得出∠1的度数为30°,在直角三角形ADC中,由CD及tan30°,利用锐角三角函数定义求出AD的长,由∠DEC为圆内接四边形ABCE的外角,利用圆内接四边形的外角等于它的内对角,得到∠DEC=∠B,由∠B的度数求出∠DEC的度数为60°,在直角三角形DEC中,由tan60°及DC的长,求出DE的长,最后由AD-ED即可求出AE的长. [来源:数理化网] 解答:(1) 证明:如图1,连接OC, ∵ CD为⊙O的切线, ∴ OC⊥CD, ∴ ∠OCD=90°. ∵ AD⊥CD, ∴ ∠ADC=90°. ∴ ∠OCD+∠ADC=180°, ∴ AD∥OC, ∴ ∠1=∠2, ∵ OA=OC, ∴ ∠2=∠3, ∴ ∠1=∠3, 即AC平分∠DAB. (2) 解法一:如图2, A B C D E O 图2 1 2 3 ∵ AB为⊙O的直径, ∴ ∠ACB=90°. 又∵ ∠B=60°, ∴ ∠1=∠3=30°. 在Rt△ACD中,CD=2, ∴ AC=2CD=4. 在Rt△ABC中,AC=4, ∴ AB===8. 连接OE, ∵ ∠EAO=2∠3=60°,OA=OE, ∴ △AOE是等边三角形, ∴ AE=OA=AB=4. 解法二:如图3,连接CE ∵ AB为⊙O的直径, A B C D E O 图3 1 2 3 ∴ ∠ACB=90°. 又∵ ∠B=60°, ∴ ∠1=∠3=30°. 在Rt△ADC中,CD=2, ∴ AD===6. ∵ 四边形ABCE是⊙O的内接四边形, ∴ ∠B+∠AEC=180°. 又∵ ∠AEC+∠DEC=180°, ∴ ∠DEC=∠B=60°. 在Rt△CDE中,CD=2, ∴ DE===2. ∴ AE=AD-DE=4. 点评:此题考查了切线的性质,平行线的性质,等边三角形的判定与性质,锐角三角函数定义,圆内接四边形的性质,以及圆周角定理,利用了转化及数形结合的思想,遇到直线与圆相切,常常连接圆心与切点,利用切线的性质得到垂直,利用直角三角形的性质来解决问题. 14.(2012•恩施州)如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB. (1)求证:BC是⊙O的切线; (2)连接AF,BF,求∠ABF的度数; (3)如果CD=15,BE=10,sinA=,求⊙O的半径. 考点: 切线的判定;勾股定理;相似三角形的判定与性质;解直角三角形。 专题: 几何综合题。 分析: (1)连接OB,有圆的半径相等和已知条件证明∠OBC=90°即可证明BC是⊙O的切线; (2)连接OF,AF,BF,首先证明△OAF是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数; (3)过点C作CG⊥BE于点G,由CE=CB,可求出EG=BE=5,又Rt△ADE∽Rt△CGE和勾股定理求出DE=2,由Rt△ADE∽Rt△CGE求出AD的长,进而求出⊙O的半径.(21世纪教育网) 解答: (1)证明:连接OB ∵OB=OA,CE=CB, ∴∠A=∠OBA,∠CEB=∠ABC 又∵CD⊥OA ∴∠A+∠AED=∠A+∠CEB=90° ∴∠OBA+∠ABC=90° ∴OB⊥BC ∴BC是⊙O的切线.(21世纪) (2)连接OF,AF,BF, ∵DA=DO,CD⊥OA, ∴△OAF是等边三角形, ∴∠AOF=60° ∴∠ABF=∠AOF=30° (3)过点C作CG⊥BE于点G,由CE=CB, ∴EG=BE=5 又Rt△ADE∽Rt△CGE ∴sin∠ECG=sin∠A=, ∴CE==13 ∴CG==12, 又CD=15,CE=13, ∴DE=2, 由Rt△ADE∽Rt△CGE得= ∴AD=•CG= ∴⊙O的半径为2AD=. 点评: 本题考查了切线的判定和性质,等边三角形的判定和性质、圆周角定理以及勾股定理和相似三角形的判定和性质,题目的综合性不小,难度也不小. 15.(2012•兰州)如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE. (1)判断DE与⊙O的位置关系并说明理由; (2)若tanC=,DE=2,求AD的长. 考点: 切线的判定;全等三角形的判定与性质;等腰三角形的性质;直角三角形斜边上的中线;解直角三角形。 专题: 计算题;证明题。(21世纪。。。。教育网) 分析: (1)连接OD,BD,求出∠ADB=∠BDC=90°,推出DE=BE=CE,推出∠EDB=∠EBD,∠OBD=∠ODB,推出∠EDO=∠EBO=90°即可; (2)BD=x,CD=2x,在Rt△BCD中,由勾股定理得出(x)2+(2x)2=16,求出x,求出BD,根据tan∠ABD=tanC求出AD=BD,代入求出即可. 解答: 解:(1)DE与⊙O相切, 理由如下:连接OD,BD, ∵AB是直径, ∴∠ADB=∠BDC=90°, ∵E是BC的中点, ∴DE=BE=CE, ∴∠EDB=∠EBD, ∵OD=OB, ∴∠OBD=∠ODB. ∴∠EDO=∠EBO=90°,(用三角形全等也可得到) ∴DE与⊙O相切. (2)∵tanC=,可设BD=x,CD=2x, ∵在Rt△BCD中,BC=2DE=4,BD2+CD2=BC2 ∴(x)2+(2x)2=16, 解得:x=±(负值舍去) ∴BD=x=, ∵∠ABD=∠C, ∴tan∠ABD=tanC AD=BD=×=. 答:AD的长是. 点评: 本题综合考查了解直角三角形,等腰三角形的性质,直角三角形斜边上中线性质,切线的判定等知识点,主要培养学生分析问题和解决问题的能力,注意:①证切线的方法,②方程思想的运用. 16.(2012•南通)(本小题满分8分) 如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB、CD的上方,求AB和CD间的距离. 【考点】垂径定理;勾股定理. 【专题】探究型. 【分析】分别作弦AB、CD的弦心距,设垂足为E、F;由于AB∥CD,则E、O、F三点共线,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,可连接OA、ODC在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离. 【解答】解:分别作弦AB、CD的弦心距,设垂足为E、F, ∵AB=30cm,CD=16cm, ∴AE=1 2 AB=1 2 ×30=15cm,CF=1 2 CD=1 2 ×16=8cm, 在Rt△AOE中, OE= OA2-AE2 = 172-152 =8cm, 在Rt△OCF中, OF= OC2-CF2 = 172-82 =15cm, ∴EF=OF-OE=15-8=7cm. 答:AB和CD的距离为8cm. 【点评】本题考查的是勾股定理及垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键. 17.(2012•常德)如图8,已知AB=AC,∠BAC=120º,在BC上取一点O,以O为圆心OB为半径作圆, ①且⊙O过A点,过A作AD∥BC交⊙O于D, 求证:(1)AC是⊙O的切线; (2)四边形BOAD是菱形。 知识点考察:①圆的切线的判定,②等腰三角形的性质, ③等边三角形的性质,④三角形内角和, ⑤平行线的性质,⑥垂直的定义, ⑦菱形的判定。(21世纪。。。。教育网) 能力考察:①观察能力,②逻辑推理能力,③书写表达能力。 分析:求证AC是⊙O的切线,则证OA⊥AC,很显然要运用圆的切线的判定定理。 要证四边形BOAD是菱形,先证BOAD为平行四边形,再证一组邻边相等。 证明:(1)∵AB=AC,∠BAC=120º, ∴∠ABC=∠C=30º 而OB=OA,∴∠BAO=∠ABC=30º, ∴∠CAO=120º-30º=90º ∴ OA⊥AC,而OA为⊙O的半径, ∴ AC是⊙O的切线。 (2)连OD,∵AD∥BC ∴ ∠DAB=∠ABC=30º, ∴∠DAO=60º 而OA=OD,∴△OAD为等边三角形, ∴OB=OA=AD, 又∵AD∥BC,∴ADBO为平行四边形, 且OA=OB ∴四边形BOAD是菱形。 点评:这是一个平面几何的综合题,主要集中在圆的切线的判定定理的运用,特殊四 边形的判定这两个方面,必须搜集、整理题目的已知条件形成清晰的思路,还 要注意推理的严谨性和完整性。 18.(2012•黔东南州)如图,⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D. (1)求证:△ABC∽△BDC. (2)若AC=8,BC=6,求△BDC的面积. 解(1)证明:∵BD是⊙O的切线, ∴AB⊥BD, ∴∠ABD=90°, ∵AB是⊙O的直径, ∴∠ACB=∠BCD=90°, ∴∠A+∠D=90°,∠CBD+∠D=90°, ∴∠A=∠CBD, ∴△ABC∽△BDC; (2)解:∵△ABC∽△BDC, ∴, ∵AC=8,BC=6, ∴S△ABC=AC•BC=×8×6=24, ∴S△BDC=S△ABC÷=24÷()2=. 19 (2012•湛江)如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D. (1)求证:AD平分∠BAC; (2)若BE=2,BD=4,求⊙O的半径. 解:(1)证明:连接OD, ∵BC是⊙O的切线, ∴OD⊥BC, 又∵AC⊥BC, ∴OD∥AC, ∴∠2=∠3; ∵OA=OD, ∴∠1=∠3, ∴∠1=∠2, ∴AD平分∠BAC; (2)解:∵BC与圆相切于点D. ∴BD2=BE•BA, ∵BE=2,BD=4, ∴BA=8, ∴AE=AB﹣BE=6, ∴⊙O的半径为3. 20. (2012•珠海)已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上. (1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果); (2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论; (3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD. 解:(1)PO与BC的位置关系是PO∥BC; (2)(1)中的结论PO∥BC成立,理由为: 由折叠可知:△APO≌△CPO, ∴∠APO=∠CPO, 又∵OA=OP, ∴∠A=∠APO, ∴∠A=∠CPO, 又∵∠A与∠PCB都为所对的圆周角, ∴∠A=∠PCB, ∴∠CPO=∠PCB, ∴PO∥BC; (3)∵CD为圆O的切线, ∴OC⊥CD,又AD⊥CD, ∴OC∥AD, ∴∠APO=∠COP, 由折叠可得:∠AOP=∠COP, ∴∠APO=∠AOP, 又OA=OP,∴∠A=∠APO, ∴∠A=∠APO=∠AOP, ∴△APO为等边三角形, ∴∠AOP=60°, 又∵OP∥BC, ∴∠OBC=∠AOP=60°,又OC=OB, ∴△BC为等边三角形, ∴∠COB=60°, ∴∠POC=180°﹣(∠AOP+∠COB)=60°,又OP=OC, ∴△POC也为等边三角形, ∴∠PCO=60°,PC=OP=OC, 又∵∠OCD=90°, ∴∠PCD=30°, 在Rt△PCD中,PD=PC, 又∵PC=OP=AB, ∴PD=AB,即AB=4PD. 21.(2012•长沙)如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°, (1)求证:△ABC是等边三角形; (2)求圆心O到BC的距离OD. 解答: 解:(1)在△ABC中, ∵∠BAC=∠APC=60°, 又∵∠APC=∠ABC, ∴∠ABC=60°, ∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°, ∴△ABC是等边三角形; (2)∵△ABC为等边三角形,⊙O为其外接圆, ∴O为△ABC的外心, ∴BO平分∠ABC, ∴∠OBD=30°, ∴OD=8×=4. 22.(2012广安)如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP. (1)求证:直线CP是⊙O的切线. (2)若BC=2,sin∠BCP=,求点B到AC的距离. (3)在第(2)的条件下,求△ACP的周长. 考点: 切线的判定与性质;等腰三角形的性质;勾股定理;相似三角形的判定与性质;解直角三角形。 专题: 几何综合题。(21世纪。。。。教育网) 分析: (1))根据∠ABC=∠AC且∠CAB=2∠BCP,在△ABC中∠ABC+∠BAC+∠BCA=180°,得到2∠BCP+2∠BCA=180°,从而得到∠BCP+∠BCA=90°,证得直线CP是⊙O的切线. (2)作BD⊥AC于点D,得到BD∥PC,从而利用sin∠BCP=sin∠DBC===,求得DC=2,再根据勾股定理求得点B到AC的距离为4. (3)先求出AC的长度,然后利用BD∥PC的比例线段关系求得CP的长度,再由勾股定理求出AP的长度,从而求得△ACP的周长. 解答: 解:(1)∵∠ABC=∠AC且∠CAB=2∠BCP,在△ABC中,∠ABC+∠BAC+∠BCA=180° ∴2∠BCP+2∠BCA=180°, ∴∠BCP+∠BCA=90°, ∴直线CP是⊙O的切线. (2)如右图,作BD⊥AC于点D, ∵PC⊥AC ∴BD∥PC ∴∠PCB=∠DBC ∵BC=2,sin∠BCP=, ∴sin∠BCP=sin∠DBC===, 解得:DC=2, ∴由勾股定理得:BD=4, ∴点B到AC的距离为4. (3)如右图,连接AN, 在Rt△ACN中,AC==5, 又CD=2,∴AD=AC﹣CD=5﹣2=3. ∵BD∥CP,∴,∴CP=. 在Rt△ACP中,AP==, AC+CP+AP=5++=20, ∴△ACP的周长为20. 点评: 本题考查了切线的判定与性质等知识,考查的知识点比较多,难度较大. 23.(2012张家界)如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线DC,P点为优弧上一动点(不与A.C重合). (1)求∠APC与∠ACD的度数; (2)当点P移动到CB弧的中点时,求证:四边形OBPC是菱形. (3)P点移动到什么位置时,△APC与△ABC全等,请说明理由. 考点:切线的性质;全等三角形的判定与性质;菱形的判定。 解答:解:(1)连接AC,如图所示: ∵AC=2,OA=OB=OC=AB=2, ∴AC=OA=OC, ∴△ACO为等边三角形, ∴∠AOC=∠ACO=∠OAC=60°, ∴∠APC=∠AOC=30°, 又DC与圆O相切于点C, ∴OC⊥DC, ∴∠DCO=90°, ∴∠ACD=∠DCO﹣∠ACO=90°﹣60°=30°;…(4分) (2)连接PB,OP, ∵AB为直径,∠AOC=60°, ∴∠COB=120°, 当点P移动到CB的中点时,∠COP=∠POB=60°, ∴△COP和△BOP都为等边三角形, ∴AC=CP=OA=OP, 则四边形AOPC为菱形;…(8分) (3)当点P与B重合时,△ABC与△APC重合,显然△ABC≌△APC; 当点P继续运动到CP经过圆心时,△ABC≌△CPA,理由为: ∵CP与AB都为圆O的直径, ∴∠CAP=∠ACB=90°, 在Rt△ABC与Rt△CPA中, , ∴Rt△ABC≌Rt△CPA(HL).…(10分) 24.(2012宜宾)如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的半径r1=2,⊙O2的半径r2=.过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C.D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A.B,连接AP、BP、AC.DB,且AC与DB的延长线交于点E. (1)求证:; (2)若PQ=2,试求∠E度数. 考点:相交两圆的性质;三角形内角和定理;圆周角定理;相似三角形的判定与性质;解直角三角形。 解答:(1)证明:∵⊙O1的半径r1=2,⊙O2的半径r2=, ∴PC=4,PD=2, ∵CD⊥PQ, ∴∠PQC=∠PQD=90°, ∴PC.PD分别是⊙O1、⊙O2的直径, 在⊙O1中,∠PAB=∠PCD, 在⊙O2中,∠PBA=∠PDC, ∴△PAB∽△PCD, ∴===, 即=. (2)解:在Rt△PCQ中,∵PC=2r1=4,PQ=2, ∴cos∠CPQ=, ∴∠CPQ=60°, ∵在Rt△PDQ中,PD=2r2=2,PQ=2, ∴sin∠PDQ=, ∴∠PDQ=45°, ∴∠CAQ=∠CPQ=60°,∠PBQ=∠PDQ=45°, 又∵PD是⊙O2的直径, ∴∠PBD=90°, ∴∠ABE=90°﹣∠PBQ=45° 在△EAB中,∴∠E=180°﹣∠CAQ﹣∠ABE=75°, 答:∠E的度数是75°. 25.(2012武汉)在锐角三角形ABC中,BC=4,sinA=, (1)如图1,求三角形ABC外接圆的直径; (2)如图2,点I为三角形ABC的内心,BA=BC,求AI的长. 考点:三角形的内切圆与内心;三角形的面积;勾股定理;圆周角定理;解直角三角形。 解答:(1)解:作直径CD,连接BD, ∵CD是直径, ∴∠DBC=90°,∠A=∠D, ∵BC=4,sin∠A=, ∴sin∠D==, ∴CD=5, 答:三角形ABC外接圆的直径是5. (2)解:连接IC.BI,且延长BI交AC于F,过I作IE⊥AB于E, ∵AB=BC=4,I为△ABC内心, ∴BF⊥AC,AF=CF, ∵sin∠A==, ∴BF=, 在Rt△ABF中,由勾股定理得:AF=CF=, AC=2AF=, ∵I是△ABC内心,IE⊥AB,IF⊥AC,IG⊥BC, ∴IE=IF=IG, 设IE=IF=IG=R, ∵△ABI、△ACI、△BCI的面积之和等于△ABC的面积, ∴AB×R+BC×R+AC×R=AC×BF, 即4×R+4×R+×R=×, ∴R=, 在△AIF中,AF=,IF=,由勾股定理得:AI=. 答:AI的长是. 26.(2012天门)如图,AB是⊙O的直径,AC和BD是它的两条切线,CO平分∠ACD. (1)求证:CD是⊙O的切线; (2)若AC=2,BC=3,求AB的长. 考点: 切线的判定与性质;勾股定理。 专题: 数形结合。 分析: (1)过O点作OE⊥CD于点E,通过角平分线的性质得出OE=OA即可证得结论. (2)过点D作DF⊥BC于点F,根据切线的性质可得出DC的长度,继而在RT△DFC中利用勾股定理可得出DF的长,继而可得出AB的长度. 解答: (1)证明:过O点作OE⊥CD,垂足为E, ∵AC是切线, ∴OA⊥AC, ∵CO平分∠ACD,OE⊥CD, ∴OA=OE, ∴CD是⊙O的切线. (2)解:过C点作CF⊥BD,垂足为E, ∵AC,CD,BD都是切线, ∴AC=CE=2,BD=DE=3, ∴CD=CE+DE=5, ∵∠CAB=∠ABD=∠CFB=90°, ∴四边形ABFC是矩形, ∴BF=AC=2,DF=BD﹣BF=1, 在Rt△CDF中,CF2=CD2﹣DF2=52﹣12=24, ∴AB=CF=2. 点评: 此题考查了切线的性质、角平分线的性质及勾股定理的知识,证明第一问关键是掌握切线的判定定理,解答第二问关键是熟练切线的性质,难度一般. 27.(2012苏州)如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4). (1)当x=时,求弦PA、PB的长度; (2)当x为何值时,PD•CD的值最大?最大值是多少? 考点: 切线的性质;二次函数的最值;勾股定理;垂径定理;相似三角形的判定与性质。 专题: 计算题。(21世纪。。。。教育网) 分析: (1)由直线l与圆相切于点A,且AB为圆的直径,根据切线的性质得到AB垂直于直线l,又PC垂直于直线l,根据垂直于同一条直线的两直线平行,得到AB与PC平行,根据两直线平行内错角相等得到一对内错角相等,再由一对直角相等,利用两对对应角相等的两三角形相似可得出三角形PCA与三角形PAB相似,由相似得比例,将PC及直径AB的长代入求出PA的长,在直角三角形PAB中,由AB及PA的长,利用勾股定理即可求出PB的长; (2)过O作OE垂直于PD,与PD交于点E,由垂径定理得到E为PD的中点,再由三个角为直角的四边形为矩形得到OACE为矩形,根据矩形的对边相等,可得出EC=OA=2,用PC﹣EC的长表示出PE,根据PD=2PE表示出PD,再由PC﹣PD表示出CD,代入所求的式子中,整理后得到关于x的二次函数,配方后根据自变量x的范围,利用二次函数的性质即可求出所求式子的最大值及此时x的取值. 解答: 解:(1)∵⊙O与直线l相切于点A,且AB为⊙O的直径, ∴AB⊥l,又∵PC⊥l, ∴AB∥PC, ∴∠CPA=∠PAB, ∵AB是⊙O的直径, ∴∠APB=90°,又PC⊥l, ∴∠PCA=∠APB=90°, ∴△PCA∽△APB, ∴=,即PA2=PC•AB, ∵PC=,AB=4, ∴PA==, ∴Rt△APB中,AB=4,PA=, 由勾股定理得:PB==; (2)过O作OE⊥PD,垂足为E, ∵PD是⊙O的弦,OE⊥PD, ∴PE=ED, 又∠CEO=∠ECA=∠OAC=90°, ∴四边形OACE为矩形, ∴CE=OA=2,又PC=x, ∴PE=ED=PC﹣CE=x﹣2, ∴CD=PC﹣PD=x﹣2(x﹣2)=4﹣x, ∴PD•CD=2(x﹣2)•(4﹣x)=﹣2x2+12x﹣16=﹣2(x﹣3)2+2, ∵2<x<4, ∴当x=3时,PD•CD的值最大,最大值是2. 点评: 此题考查了切线的性质,平行线的性质,矩形的判定与性质,垂径定理,勾股定理,相似三角形的判定与性质,以及二次函数的性质,熟练掌握性质及定理是解本题的关键. 28.(2012陕西)(本题满分8分) 如图,分别与相切于点,点在上,且,,垂足为. (1)求证:; (2)若的半径,,求的长. 【答案】解:(1)证明:如图,连接,则. ∵, ∴. ∵, ∴四边形是矩形. ∴. (2)连接,则. ∵,,, ∴,. ∴. ∴. 设,则. 在中,有. ∴.即. 29.(2012岳阳)如图所示,在⊙O中,=,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. (1)求证:AC2=AB•AF; (2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积. 考点: 扇形面积的计算;圆心角、弧、弦的关系;圆周角定理;相似三角形的判定与性质。1052629(21世纪。。。。教育网) 专题: 几何综合题。(21世纪。。。。教育网) 分析: (1)由=,利用等弧所对的圆周角相等得到一对角相等,再由一对公共角相等,利用两对对应角相等的两三角形相似可得出△ACF与△ABC相似,根据相似得比例可得证; (2)连接OA,OC,利用同弧所对的圆心角等于圆周角的2倍,由∠B为60°,求出∠AOC为120°,过O作OE垂直于AC,垂足为点E,由OA=OC,利用三线合一得到OE为角平分线,可得出∠AOE为60°,在Rt△AOE中,由OA及cos60°的值,利用锐角三角函数定义求出OE的长,在Rt△AOE中,利用勾股定理求出AE的长, 进而求出AC的长,由扇形AOC的面积﹣△AOC的面积表示出阴影部分的面积,利用扇形的面积公式及三角形的面积公式即可求出阴影部分的面积. 解答: (1)证明:∵=, ∴∠ACD=∠ABC,又∠BAC=∠CAF, ∴△ACF∽△ABC, ∴=,即AC2=AB•AF; (2)解:连接OA,OC,过O作OE⊥AC,垂足为点E, 如图所示: ∵∠ABC=60°,∴∠AOC=120°, 又OA=OC,∴∠AOE=∠COE=×120°=60°, 在Rt△AOE中,OA=2cm, ∴OE=OAcos60°=1cm, ∴AE==cm, ∴AC=2AE=2cm, 则S阴影=S扇形OAC﹣S△AOC=﹣×2×1=(﹣)cm2. 点评: 此题考查了扇形面积的求法,涉及的知识有:相似三角形的判定与性质,弧、圆心角及弦之间的关系,等腰三角形的性质,勾股定理,以及锐角三角函数定义,熟练掌握性质及定理是解本题的关键. 30.(2012泰州)如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C. (1)试判断线段AB与AC的数量关系,并说明理由; (2)若PC=,求⊙O的半径和线段PB的长; (3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围. 【答案】解:(1)AB=AC。理由如下: 连接OB。 ∵AB切⊙O于B,OA⊥AC,∴∠OBA=∠OAC=90°。 ∴∠OBP+∠ABP=90°,∠ACP+∠CPB=90°。 ∵OP=OB,∴∠OBP=∠OPB。 ∵∠OPB=∠APC,∴∠ACP=∠ABC。 ∴AB=AC。 (2)延长AP交⊙O于D,连接BD, 设圆半径为r,则由OA=5得,OP=OB=r,PA=5-r。 又∵PC=, ∴ 。 由(1)AB=AC得,解得:r=3。 ∴AB=AC=4。 ∵PD是直径,∴∠PBD=90°=∠PAC。 ∵∠DPB=∠CPA,∴△DPB∽△CPA。∴,即,解得。 (3)作线段AC的垂直平分线MN,作OE⊥MN,[来源:数理化网] 则OE=AC=AB=。 又∵圆O要与直线MN交点,∴OE=≤r, ∴r≥。 又∵圆O与直线l相离,∴r<5。 ∴⊙O的半径r的取值范围为≤r<5. (2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5-r,根据AB=AC推出 ,求出r,证△DPB∽△CPA,得出 ,代入求出PB即可。 (3)根据已知得出Q在AC的垂直平分线上,作出线段AC的垂直平分线MN,作OE⊥MN,求出OE<r,求出r范围,再根据相离得出r<5,即可得出答案。21世纪教育网 31.(2012•宁波)如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F. (1)求证:AC是⊙O的切线; (2)已知sinA=,⊙O的半径为4,求图中阴影部分的面积. 考点: 切线的判定;扇形面积的计算。21cnjy 分析: (1)连接OE.根据OB=OE得到∠OBE=∠OEB,然后再根据BE是△ABC的角平分线得到∠OEB=∠EBC,从而判定OE∥BC,最后根据∠C=90°得到∠AEO=∠C=90°证得结论AC是⊙O的切线. (2)连接OF,利用S阴影部分=S梯形OECF﹣S扇形EOF求解即可.21cnjy 解答: 解:(1)连接OE. ∵OB=OE ∴∠OBE=∠OEB ∵BE是△ABC的角平分线 ∴∠OBE=∠EBC ∴∠OEB=∠EBC ∴OE∥BC ∵∠C=90° ∴∠AEO=∠C=90° ∴AC是⊙O的切线; (2)连接OF. ∵sinA=,∴∠A=30° ∵⊙O的半径为4,∴AO=2OE=8, ∴AE=4,∠AOE=60°,∴AB=12, ∴BC=AB=6 AC=6, ∴CE=AC﹣AE=2. ∵OB=OF,∠ABC=60°,∴△OBF是正三角形. ∴∠FOB=60°,CF=6﹣4=2,∴∠EOF=60°. ∴S梯形OECF=(2+4)×2=6. S扇形EOF== ∴S阴影部分=S梯形OECF﹣S扇形EOF=6﹣. 点评: 本题考查了切线的判定与性质及扇形面积的计算,解题的关键是连接圆心和切点,利用过切点且垂直于过切点的半径来判定切线. 32.(2012•宜昌)如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为的中点. (1)求证:OF∥BD; (2)若,且⊙O的半径R=6cm. ①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积. 考点: 相似三角形的判定与性质;等边三角形的判定与性质;圆心角、弧、弦的关系;圆周角定理;扇形面积的计算。1419956 专题: 几何综合题。 分析: (1)由垂径定理可知OC⊥AD,由圆周角定理可知BD⊥AD,从而证明OF∥BD; (2)①由OF∥BD可证△ECF∽△EBD,利用相似比证明BD=2CF,再证OF为△ABD的中位线,得出BD=2OF,即CF=OF,证明点F为线段OC的中点; ②根据S阴=S扇形AOC﹣S△AOC,求面积. 解答: (1)证明:∵OC为半径,点C为AD的中点,∴OC⊥AD, ∵AB为直径,∴∠BDA=90°,BD⊥AD, ∴OF∥BD; (2)证明:①∵点O为AB的中点,点F为AD的中点, ∴OF=BD, ∵FC∥BD,∴∠FCE=∠DBE, ∵∠FEC=∠DEB,∴△ECF∽△EBD, ∴,∴FC=BD, ∴FC=FO,即点F为线段OC的中点, ②解:∵FC=FO,OC⊥AD,∴AC=AO, 又∵AO=CO,∴△AOC为等边三角形, ∴S阴==6π﹣9(cm2), 答:图中阴影部分(弓形)的面积为(6π﹣9)cm2. 点评: 本题考查了相似三角形的判定与性质,等边三角形的判定与性质,垂径定理,圆周角定理,扇形面积的计算.关键是熟练掌握各知识点的联系及互相转化. 33.(2012•柳州)如图,AB是⊙O的直径,AC是弦. (1)请你按下面步骤画图(画图或作辅助线时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑); 第一步,过点A作∠BAC的角平分线,交⊙O于点D; 第二步,过点D作AC的垂线,交AC的延长线于点E. 第三步,连接BD. (2)求证:AD2=AE•AB; (3)连接EO,交AD于点F,若5AC=3AB,求的值. 【考点】圆的综合题. 【专题】综合题. 【分析】(1)根据基本作图作出∠BAC的角平分线AD交⊙O于点D;点D作AC的垂线,垂足为点E; (2)根据直径所对的圆周角为直角得到∠ADB=90°,DE⊥AC,则∠AED=90°,又由AD平分∠CAB得到∠CAD=∠DAB,根据相似三角形的判定得到Rt△ADE∽Rt△ABD,根据相似的性质得到AD:AB=AE:AD,利用比例的性质即可得到AD2=AE•AB; (3)连OD、BC,它们交于点G,由5AC=3AB,则不妨设AC=3x,AB=5x,根据直径所对的圆周角为直角得到∠ACB=90°,由∠CAD=∠DAB得到,根据垂径定理的推论得到OD垂直平分BC,则有OD∥AE,OG=AC=x,并且得到四边形ECGD为矩形,则CE=DG=OD-OG=x-x=x,可计算出AE=AC+CE=3x+x=4x,利用AE∥OD可得到△AEF∽△DOF,则AE:OD=EF:OF,即EF:OF=4x:x=8:5,然后根据比例的性质即可得到 的值. 【解答】(1)解:如图; (2)证明:∵AB是⊙O的直径, ∴∠ADB=90°, 而DE⊥AC, ∴∠AED=90°, ∵AD平分∠CAB, ∴∠CAD=∠DAB, ∴Rt△ADE∽Rt△ABD, ∴AD:AB=AE:AD, ∴AD2=AE•AB; (3)解:连OD、BC,它们交于点G,如图, ∵5AC=3AB,即AC:AB=3:5, ∴不妨设AC=3x,AB=5x, ∵AB是⊙O的直径, ∴∠ACB=90°, 又∵∠CAD=∠DAB, ∴, ∴OD垂直平分BC, ∴OD∥AE,OG=1 2 AC=3 2 x, ∴四边形ECGD为矩形, ∴CE=DG=OD-OG=x-x =x, ∴AE=AC+CE=3x+x=4x, ∵AE∥OD, ∴△AEF∽△DOF, ∴AE:OD=EF:OF, ∴EF:OF=4x:x=8:5, ∴ . 【点评】本题考查了圆的综合题:平分弦所对的弧的直径垂直平分弦;在同圆或等圆中,相等的圆周角所对的弧相等;直径所对的圆周角为直角;运用相似三角形的判定与性质证明等积式和几何计算;掌握基本的几何作图. 34. (2012•吉林)如图,在扇形中,,半径.将扇形沿过点的直线折叠.点恰好落在上点处,折痕交于点,求整个阴影部分的周长和面积. [答案] 周长:;面积:. [考点] 图形的折叠:折叠前、后的图形全等;全等三角形的性质:全等三角形对应边相等,全等三角形对应角相等;圆:弧长和扇形面积:弧长,.正三角形的判定:三边相等的三角形是正三角形.正三角形的性质.锐角三角函数:解直角三角形. [解析] 如图(第23题),由折叠前、后的图形全等.所以,,,.又在扇形中,,半径.所以,,,的长.所以, 整个阴影部分的周长的长. 如图(第23题-1),连接扇形的半径, 由正三角形,在中,, 所以,整个阴影部分的面积 35. (2012广元)如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD ⊥CD (1)求证:AE平分∠DAC; (2)若AB=3,∠ABE=60°, ①求AD的长;②求出图中阴影部分的面积。 【答案】解:(1)证明:连接OE。 ∵CD是⊙O的切线,∴OE⊥CD。 ∵AD⊥CD,∴AD∥OE。∴∠DAE=∠AEO。 ∵OA=OE,∴∠EAO=∠AEO。 ∴∠DAE=∠EAO。∴AE平分∠DAC。 (2)①∵AB是⊙O的直径,∴∠AEB=90°。 ∵∠ABE=60°,∴∠EAO=30°。∴∠DAE=∠EAO=30°。 ∵AB=3,∴在Rt△ABE中, 在Rt△ADE中,∵∠DAE=30°,AE= ,∴。 ②∵∠EAO=∠AEO=30°,∴。 ∵OA=OB,∴。 ∴ 。 【考点】切线的性质,平行的判定和性质,圆周角定理,锐角三角函数定义,特殊角的三角函数值,三角形内角和定理,扇形面积的计算。 【分析】(1)连接OE,由切线的性质可知,OE⊥CD,再根据AD⊥CD可知AD∥OE,故∠DAE=∠AEO, 再由OA=OE可知∠EAO=∠AEO,故∠DAE=∠EAO,故可得出结论。 (2)①根据∠ABE=60°求出∠EAO的度数,进而得出∠DAE的度数,再根据锐角三角函数的定 义求出AE及BE的长,在Rt△ADE中利用锐角三角函数的定义即可得出AD的长。 ②由三角形内角和定理求出∠AOE的度数,再根据OA=OB可知求 出△AOE的面积,由即可得出结论。 2011年全国各地中考数学压轴题汇编 第31章 与圆有关的解答题 1. (2011浙江义乌,21,8分)如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的 延长线相交于点F,且AD=3,cos∠BCD= . (1)求证:CD∥BF; (2)求⊙O的半径; (3)求弦CD的长. FM A DO EC O C B 【答案】(1)∵BF是⊙O的切线 ∴AB⊥BF ∵AB⊥CD ∴CD∥BF (2)连结BD ∵AB是直径 ∴∠ADB=90° ∵∠BCD=∠BAD cos∠BCD= ∴cos∠BAD= 又∵AD=3 ∴AB=4 ∴⊙O的半径为2 F A D E O C B (3)∵cos∠DAE= AD=3∴AE= ∴ED= ∴CD=2ED= 2. (2011浙江省舟山,22,10分)如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC. (1)求证:CA是圆的切线; (2)若点E是BC上一点,已知BE=6,tan∠ABC=,tan∠AEC=,求圆的直径. (第22题) 【答案】(1)∵BC是直径,∴∠BDC=90°,∴∠ABC+∠DCB=90°,∵∠ACD=∠ABC, ∴∠ACD+∠DCB=90°,∴BC⊥CA,∴CA是圆的切线. (2)在Rt△AEC中,tan∠AEC=,∴,; 在Rt△ABC中,tan∠ABC=,∴,; ∵BC-EC=BE,BE=6,∴,解得AC=, ∴BC=.即圆的直径为10. 3. (2011安徽芜湖,23,12分)如图,已知直线交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作,垂足为D. (1) 求证:CD为⊙O的切线; (2) 若DC+DA=6,⊙O的直径为10,求AB的长度. 【答案】 (1)证明:连接OC, ……………………………………1分 因为点C在⊙O上,OA=OC,所以 因为,所以,有.因为AC平分∠PAE,所以……………3分 所以 ……4分 又因为点C在⊙O上,OC为⊙O的半径,所以CD为⊙O的切线. ………………5分 (2)解:过O作,垂足为F,所以, 所以四边形OCDF为矩形,所以 ……………………………7分 因为DC+DA=6,设,则 因为⊙O的直径为10,所以,所以. 在中,由勾股定理知 即化简得, 解得或x=9. ………………9分 由,知,故. ………10分 从而AD=2, …………………11分 因为,由垂径定理知F为AB的中点,所以…………12分 4. (2011山东滨州,22,8分)如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM, 连接OM、BC. 求证:(1)△ABC∽△POM; (2)2OA2=OP·BC. (第22题图) [来源:www.shulihua.net] 【答案】证明:(1)∵直线PM切⊙O于点M,∴∠PMO=90°………………1分 ∵弦AB是直径,∴∠ACB=90°………………2分 ∴∠ACB=∠PMO………………3分 ∵AC∥PM, ∴∠CAB=∠P ………………4分 ∴△ABC∽△POM………………5分 (2) ∵ △ABC∽△POM, ∴………………6分 又AB=2OA,OA=OM, ∴………………7分 ∴2OA2=OP·BC………………8分 5. (2011山东菏泽,18,10分)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4, (1)求证:△ABE∽△ADB; (2)求AB的长; (3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由. 解:(1)证明:∵AB=AC,∴∠ABC=∠C, ∵∠C=∠D,∴∠ABC=∠D, 又∵∠BAE=∠EAB,∴△ABE∽△ADB, (2) ∵△ABE∽△ADB,∴, ∴AB2=AD·AE=(AE+ED)·AE=(2+4)×2=12 ∴AB=. (3) 直线FA与⊙O相切,理由如下: 连接OA,∵BD为⊙O的直径,∴∠BAD=90°, ∴, BF=BO=, ∵AB=,∴BF=BO=AB,可证∠OAF=90°, ∴直线FA与⊙O相切. 6. (2011山东日照,21,9分)如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D. 求证:(1)∠AOC=2∠ACD; (2)AC2=AB·AD. 【答案】证明:(1)∵CD是⊙O的切线,∴∠OCD=90°, 即∠ACD+∠ACO=90°.…① ∵OC=OA,∴∠ACO=∠CAO, ∴∠AOC=180°-2∠ACO,即∠AOC+∠ACO=90°. ② 由①,②,得:∠ACD-∠AOC=0,即∠AOC=2∠ACD; (2)如图,连接BC. ∵AB是直径,∴∠ACB=90°. 在Rt△ACD与△RtACD中, ∵∠AOC=2∠B,∴∠B=∠ACD, ∴△ACD∽△ABC,∴,即AC2=AB·AD. 7. (2011浙江温州,20,8分)如图,AB是⊙O的直径,弦CD⊥AB于点E,过点B作⊙O的切线,交AC的延长线于点F.已知OA=3,AE=2, (1)求CD的长; (2)求BF的长. 【答案】解:(1)连结OC,在Rt△OCE中,. ∵CD⊥AB, ∴ (2) ∵BF是⊙O 的切线, ∴FB⊥AB, ∴CE∥FB, ∴△ACE∽△AFB, ∴,, ∴ 8. (2011浙江省嘉兴,22,12分)如图,△ABC中,以BC为直径的圆交AB于点D ,∠ACD=∠ABC. (1)求证:CA是圆的切线; (2)若点E是BC上一点,已知BE=6,tan∠ABC=,tan∠AEC=,求圆的直径. (第22题) 【答案】(1)∵BC是直径,∴∠BDC=90°,∴∠ABC+∠DCB=90°,∵∠ACD=∠ABC, ∴∠ACD+∠DCB=90°,∴BC⊥CA,∴CA是圆的切线. (2)在Rt△AEC中,tan∠AEC=,∴,; 在Rt△ABC中,tan∠ABC=,∴,; ∵BC-EC=BE,BE=6,∴,解得AC=, ∴BC=.即圆的直径为10. 9. (2011广东株洲,22,8分)如图,AB为⊙O的直径,BC为⊙O的切线,AC交⊙O于点E,D 为AC上一点,∠AOD=∠C. (1)求证:OD⊥AC; (2)若AE=8,,求OD的长. 【答案】(1)证明:∵BC是⊙O的切线,AB为⊙O的直径 ∴∠ABC=90°,∠A+∠C=90°, 又∵∠AOD=∠C, ∴∠AOD+∠A=90°, ∴∠ADO=90°, ∴OD⊥AC. (2)解:∵OD⊥AE,O为圆心, ∴D为AE中点 , ∴, 又 ,∴ OD=3. 10.(2011山东济宁,20,7分)如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF, (1)求证:OD∥BE; (2)猜想:OF与CD有何数量关系?并说明理由. 第20题 【答案】(1)证明:连接OE, ∵AM、DE是⊙O的切线,OA、OE是⊙O的半径, ∴∠ADO=∠EDO,∠DAO=∠DEO=90°, ∴∠AOD=∠EOD=∠AOE, ∵∠ABE=∠AOE,∴∠AOD=∠ABE, ∴OD∥BE (2)OF=CD, 理由:连接OC, ∵BC、CE是⊙O的切线, ∴∠OCB=∠OCE ∵AM∥BN, ∴∠ADO+∠EDO+∠OCB+∠OCE=180° 由(1)得∠ADO=∠EDO, ∴2∠EDO+2∠OCE=180°,即∠EDO+∠OCE=90° 在Rt△DOC中,∵F是DC的中点, ∴OF=CD. 第20题 11. (2011山东聊城,23,8分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是的中点,连接OD、AE,过点D作DP∥AE交BA的延长线于点P, (1)求∠AOD的度数; (2)求证:PD是半圆O的切线; 【答案】(1)∵点C是OA的中点,∴OC=OA=OD,∵CD⊥OA,∴∠OCD=90°,在Rt△OCD中,cos∠COD=,∴∠COD=60°,即∠AOD=60°, (2)证明:连接OC,点E是BD弧的中点,DE弧=BE弧,∴∠BOE=∠DOE=∠DOB= (180°-∠COD)=60°,∵OA=OE,∴∠EAO=∠AEO,又∠EAO+∠AEO=∠EOB=60°,∴∠EAO=30°,∵PD∥AE,∴∠P=∠EAO=30°,由(1)知∠AOD=60°,∴∠PDO=180°-(∠P+∠POD)=180°-(30°+60°)=90°,∴PD是圆O的切线 12. (2011山东潍坊,23,11分)如图,AB是半圆O的直径,AB=2.射线AM、BN为半圆的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点做半圆的切线DP,切点为P,与BN相交于点Q.[来源:www.shulihua.net] (1)求证:△ABC∽ΔOFB; (2)当ΔABD与△BFO的面积相等时,求BQ的长; (3)求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点. 【解】(1)证明:∵AB为直径, ∴∠ACB=90°,即AC⊥BC. 又∵OE⊥BC,∴OE//AC,∴∠BAC=∠FOB. ∵BN是半圆的切线,故∠BCA=∠OBF=90°. ∴△ACB∽△OBF. (2)由△ACB∽△OBF,得∠OFB=∠DBA,∠DAB=∠OBF=90°, ∴△ABD∽△BFO, 当△ABD与△BFO的面积相等时,△ABD≌△BFO. ∴AD=BO=AB =1. ∵DA⊥AB,∴DA为⊙O的切线. 连接OP,∵DP是半圆O的切线, ∴DA=DP=1,∴DA=AO=OP=DP=1, ∴四边形ADPO为正方形. ∴DP//AB,∴四边形DABQ为矩形. ∴BQ=AD=1. (3)由(2)知,△ABD∽△BFO, ∴,∴. ∵DPQ是半圆O的切线,∴AD=DP,QB=QP. 过点Q作AM的垂线QK,垂足为K,在Rt△DQK中,, ∴, ∴,∴BF=2BQ,∴Q为BF的中点. 13. (2011四川广安,29,10分)如图8所示.P是⊙O外一点.PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,并延长BO与切线PA相交于点Q. (1)求证:PB是⊙O的切线; (2)求证: AQ·PQ= OQ·BQ; (3)设∠AOQ=.若cos=.OQ= 15.求AB的长 _ Q _ P _ O _ B _ A 图8 【答案】(1)证明:如图,连结OP ∵PA=PB,AO=BO,PO=PO ∴△APO≌△BPO ∴∠PBO=∠PAO=90° ∴PB是⊙O的切线 (2)证明:∵∠OAQ=∠PBQ=90° ∴△QPB∽QOA ∴ 即AQ·PQ= OQ·BQ (3)解:cos== ∴AO=12 ∵△QPB∽QOA ∠BPQ=∠AOQ= ∴tan∠BPQ== ∴PB=36 PO=12 ∵AB·PO= OB·BP ∴AB= _ Q _ P _ O _ B _ A 图8 14. (2011江苏淮安,25,10分)如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,∠DAB=∠B=30°. (1)直线BD是否与⊙O相切?为什么?(2)连接CD,若CD=5,求AB的长. 【答案】(1)答:直线BD与⊙O相切.理由如下: 如图,连接OD, ∵∠ODA=∠DAB=∠B=30°, ∴∠ODB=180°-∠ODA-∠DAB-∠B=180°-30°-30°-30°=90°, 即OD⊥BD, ∴直线BD与⊙O相切. (2)解:由(1)知,∠ODA=∠DAB=30°, ∴∠DOB=∠ODA+∠DAB=60°, 又∵OC=OD, ∴△DOB是等边三角形, ∴OA=OD=CD=5. 又∵∠B=30°,∠ODB=30°, ∴OB=2OD=10. ∴AB=OA+OB=5+10=15. 15. (2011江苏南通,22,8分)(本小题满分8分) 如图,AM为⊙O的切线,A为切点,BD⊥AM于点D,BD交⊙O于C,OC平分∠AOB.求∠B的度数. 【答案】60°. 16. (2011四川绵阳22,12)如图,在梯形ABCD中,AB//CD,∠BAD=90°,以AD为直径的 半圆O与BC相切. (1)求证:OB丄OC; (2)若AD= 12,∠ BCD=60°,⊙O1与半⊙O 外切,并与BC、CD 相切,求⊙O1的面积. 【答案】(1)证明:连接OF,在梯形ABCD,在直角△AOB 和直角△AOB F中 ∵ ∴△AOB≌△AOB(HL) 同理△COD≌△COF,∴∠BOC=90°,即OB⊥OC (2) 过点做O1G,O1H垂直DC,DA,∵∠DOB=60°,∴∠DCO=∠BCO=30°,设O1G=x,又∵AD=12,∴OD=6,DC=6,OC=12,CG=x, O1C =6-x,根据勾股定理可知O1G²+GC²=O1C² x²+3x²=(6-x)²∴(x-2)(x+6)=0,x=2 17. (2011四川乐山24,10分)如图,D为O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)求证:CD是⊙O的切线; (2)过点B作O的切线交CD的延长线于点E,若BC=6,tan∠CDA=,求BE的长 【答案】 ⑴证明:连接OD ∵OA=OD ∴∠ADO=∠OAD ∵AB为⊙O的直径, ∴∠ADO+∠BDO=90° ∴在RtΔABD中,∠ABD+∠BAD=90° ∵∠CDA=∠CBD ∴∠CDA+∠ADO=90° ∴OD⊥CE 即CE为⊙O的切线 18. (2011四川凉山州,27,8分)如图,已知,以为直径,为圆心的半圆交于点,点为的中点,连接交于点,为的角平分线,且,垂足为点。 (1) 求证:是半圆的切线; (2) 若,,求的长。 B DA OA HA CA EA MA FA A 27题图 【答案】 ⑴证明:连接, ∵是直径 ∴ 有∵于 ∴ ∵ ∴ ∵是的角平分线 ∴ 又 ∵为的中点 ∴ ∵于 ∵ 即 又∵是直径 ∴是半圆的切线 ···4分 (2)∵,。 由(1)知,,∴。 在中,于,平分, ∴,∴。 由∽,得。 ∴, ∴。 19. (2011江苏无锡,27,10分)(本题满分10分)如图,已知O(0,0)、A(4,0)、B(4,3)。动点P从O点出发,以每秒3个单位的速度,沿△OAB的边OA、AB、BO作匀速运动;动直线l从AB位置出发,以每秒1个单位的速度向x轴负方向作匀速平移运动。若它们同时出发,运动的时间为t秒,当点P运动到O时,它们都停止运动。 (1)当P在线段OA上运动时,求直线l与以点P为圆心、1为半径的圆相交时t的取值范围; (2)当P在线段AB上运动时,设直线l分别与OA、OB交于C、D,试问:四边形CPBD是否可能为菱形?若能,求出此时t的值;若不能,请说明理由,并说明如何改变直线l的出发时间,使得四边形CPBD会是菱形。 y O x A B 【答案】 解:(1)当点P在线段OA上时,P(3t,0),…………………………………………………………(1分) ⊙P与x轴的两交点坐标分别为(3t − 1,0)、(3t + 1,0),直线l为x = 4 − t, 若直线l与⊙P相交,则……………(3分) 解得: < t < .……………………………………………………………………(5分) (2)点P与直线l运动t秒时,AP = 3t − 4,AC = t.若要四边形CPBD为菱形,则CP // OB, ∴∠PCA = ∠BOA,∴Rt△APC ∽ Rt△ABO,∴,∴,解得t = ,……(6分) 此时AP = ,AC = ,∴PC = ,而PB = 7 − 3t = ≠ PC, 故四边形CPBD不可能时菱形.……………………………………………(7分) (上述方法不唯一,只要推出矛盾即可) 现改变直线l的出发时间,设直线l比点P晚出发a秒, 若四边形CPBD为菱形,则CP // OB,∴△APC ∽ △ABO,,∴, 即:,解得 ∴只要直线l比点P晚出发秒,则当点P运动秒时,四边形CPBD就是菱形.………………(10分) 20.(2011湖北武汉市,22,8分)(本题满分8分)如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E. (1)求证:PB为⊙O的切线; (2)若tan∠ABE=,求sinE的值. 【答案】(本题8分)(1)证明:连接OA ∵PA为⊙O的切线, ∴∠PAO=90° ∵OA=OB,OP⊥AB于C ∴BC=CA,PB=PA ∴△PBO≌△PAO ∴∠PBO=∠PAO=90° ∴PB为⊙O的切线 (2)解法1:连接AD,∵BD是直径,∠BAD=90° 由(1)知∠BCO=90° ∴AD∥OP ∴△ADE∽△POE ∴EA/EP=AD/OP 由AD∥OC得AD=2OC ∵tan∠ABE=1/2 ∴OC/BC=1/2,设OC=t,则BC=2t,AD=2t由△PBC∽△BOC,得PC=2BC=4t,OP=5t ∴EA/EP=AD/OP=2/5,可设EA=2m,EP=5m,则PA=3m ∵PA=PB∴PB=3m ∴sinE=PB/EP=3/5 (2)解法2:连接AD,则∠BAD=90°由(1)知∠BCO=90°∵由AD∥OC,∴AD=2OC ∵tan∠ABE=1/2,∴OC/BC=1/2,设OC=t,BC=2t,AB=4t由△PBC∽△BOC,得PC=2BC=4t, ∴PA=PB=2t 过A作AF⊥PB于F,则AF·PB=AB·PC ∴AF=t 进而由勾股定理得PF=t ∴sinE=sin∠FAP=PF/PA=3/5 21. (2011湖南衡阳,24,8分)如图,△ABC内接于⊙O,CA=CB,CD∥AB且与OA的延长线交与点D. (1)判断CD与⊙O的位置关系并说明理由; (2)若∠ACB=120°,OA=2,求CD的长. 【解】 (1) CD与⊙O的位置关系是相切,理由如下: 作直径CE,连结AE. ∵CE是直径, ∴∠EAC=90°,∴∠E+∠ACE=90°, ∵CA=CB,∴∠B=∠CAB,∵AB∥CD, ∴∠ACD=∠CAB,∵∠B=∠E,∠ACD=∠E, ∴∠ACE+∠ACD=90°,即∠DCO=90°, ∴OC⊥D C,∴CD与⊙O相切. (2)∵CD∥AB,OC⊥D C,∴OC⊥A B, 又∠ACB=120°,∴∠OCA=∠OCB=60°, ∵OA=OC,∴△OAC是等边三角形, ∴∠DOA=60°, ∴在Rt△DCO中, =, ∴DC=OC=OA=2. 22. (2011湖南永州,23,10分)如图,AB是半圆O的直径,点C是⊙O上一点(不与A,B重合),连接AC,BC,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,连接EB,使∠OEB=∠ABC. ⑴求证:BE是⊙O的切线; ⑵若OA=10,BC=16,求BE的长. (第25题图) 【答案】证明:⑴∵AB是半圆O的直径 ∴∠ACB=90° ∵OD∥AC ∴∠ODB=∠ACB=90° ∴∠BOD+∠ABC=90° 又∵∠OEB=∠ABC ∴∠BOD+∠OEB=90° ∴∠OBE=90° ∵AB是半圆O的直径 ∴BE是⊙O的切线 ⑵在中,AB=2OA=20,BC=16,∴ ∴ ∴ ∴. 23. (2011江苏盐城,25,10分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F. (1)若AC=6,AB= 10,求⊙O的半径; (2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由. 【答案】(1)连接OD. 设⊙O的半径为r. ∵BC切⊙O于点D,∴OD⊥BC. ∵∠C=90°,∴OD∥AC,∴△OBD∽△ABC. ∴ = ,即 = . 解得r = , ∴⊙O的半径为. (2)四边形OFDE是菱形. ∵四边形BDEF是平行四边形,∴∠DEF=∠B. ∵∠DEF=∠DOB,∴∠B=∠DOB. ∵∠ODB=90°,∴∠DOB+∠B=90°,∴∠DOB=60°. ∵DE∥AB,∴∠ODE=60°.∵OD=OE,∴△ODE是等边三角形. ∴OD=DE.∵OD=OF,∴DE=OF.∴四边形OFDE是平行四边形. ∵OE=OF,∴平行四边形OFDE是菱形. 24. (20011江苏镇江27,9分)在平面直角坐标系xOy中,一次函数的图象是直线与x轴、y轴分别相交于A、B两点.直线过点C(a,0)且与垂直,其中a>0,点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位. (1)写出A点的坐标和AB的长; (2)当点P、Q运动了t秒时,以点Q为圆心,PQ为半径的⊙Q与直线、y轴都相切,求此时a的值. 答案:(1)A(-4,0),AB=5. (2)由题意得:AP=4t,AQ=5t,,又∠PAQ=∠QAB,∴△APQ∽△AOB. ∴∠APQ=∠AOB=90°。 ∵点P在上,∴⊙Q在运动过程中保持与相切。 ①当⊙Q在y轴右侧与y轴相切时,设与⊙Q相切于F,由△APQ∽△AOB得 ,∴PQ=6, 连接QF,则QF=PQ, △QFC∽△APQ∽△AOB得. ∴,,∴QC=,a=OQ+QC=. ②当⊙Q在y轴左侧与y轴相切时,设与⊙Q相切于E, 由△APQ∽△AOB得 ,∴PQ=. 连接QE,则QE=PQ,由△QEC∽△APQ∽△AOB得,∴,, ∴QC=,a=QC-OQ=.∴a的值为和。 25. (2011广东湛江27,12分)如图,在中,,点D是AC的中点,且,过点作,使圆心在上,与交于点. (1)求证:直线与相切; (2)若,求的直径. 【答案】(1)证明:连接OD,在中,OA=OD, 所以, 又因为, 所以,所以,即, 所以BD与相切; (2)由于AE为直径,所以,由题意可知,又点D是AC的中点,且 ,所以可得,即的直径为5. 26. (2011贵州安顺,26,12分)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E. ⑴求证:点D是AB的中点; ⑵判断DE与⊙O的位置关系,并证明你的结论; ⑶若⊙O的直径为18,cosB =,求DE的长. 第26题图 【答案】(1)证明:连接CD,则CD, 又∵AC = BC, CD = CD, ∴≌ ∴AD = BD , 即点D是AB的中点. 第26题图 (2)DE是⊙O的切线 . 理由是:连接OD, 则DO是△ABC的中位线,∴DO∥AC , 又∵DE; ∴DE 即DE是⊙O的切线; (3)∵AC = BC, ∴∠B =∠A , ∴cos∠B = cos∠A =, ∵ cos∠B =, BC = 18, ∴BD = 6 , ∴AD = 6 , ∵ cos∠A = , ∴AE = 2, 在中,DE=. 27. (2011河北,25,10分)如图14-1至14-4中,两平行线AB,CD间的距离为6,点M为AB上一定点. 思考 如图14-1,圆心为O的半圆纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α. 当α= 度时,点P到CD的距离最小,最小值为 。 探究一 在图14-1的基础上,以点M为旋转中心,在AB,CD之间顺时针旋转该半圆纸片,直到不能再转动为止,如图14-2,得到最大旋转角∠BMO= 度,此时点N到CD的距离是 探究二 将图14-1中的扇形纸片NOP按下面对α要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转。 (1)如图14-3,当α=60°时,球在旋转过程中,点p到CD的最小距离,并请指出旋转角∠BMO的最大值; (2)如图14-4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围. (参考数据:sin49°=,cos41°=,tan37°= ) 【答案】思考 90,2; 探究一 30,2; 探究二 (1)由已知得M与P的距离为4,∴当MP⊥AB时,点P到AB的最大距离为4,从而点P到CD的最小距离为6-4=2.当扇形MOP在AB,CD之间旋转到不能再转时,弧MP与AB相切,此时旋转角最大,∠BMO的最大值为90°。 (2)如图,由探究一可知,点P是弧MP与CD的切点时,α达到最大,即OP⊥CD。此时延长PO交AB于点H,α最大值为∠OMH+∠OHM=30°+90°=120°。 如图,当点P在CD上且与AB距离最小时,MP⊥CD,α达到最小,连接MP,作OH⊥MP于点H,由垂径定理,得MH=3,在Rt△MOH中,MO=4,∴sin∠MOH=,∴∠MOH=49°,∵α=2∠MOH,∴α最小值为98°。∴α的取值范围是98°≤α≤120°。 28. (2011江西,20,8分)有一种用来画圆的工具板(如图所示),工具板长21cm,上面依次排列着大小不等的五个圆(孔),共中最大圆的直径为3cm,其余圆的直径从左到右依次递减0.2cm.最大圆的左侧距工具板左侧边缘1.5cm,最小圆的右侧距工具板右侧边缘1.5cm,相邻两圆的间距d均相等。 ⑴直接写出其余四个圆的直径长; ⑵求相邻两圆的间距。 【答案】(1)其余四个圆的直径长分别为2.8cm,2.6cm,2.4cm,2.2cm; (2)因为工具板长21cm,左、右侧边缘1.5cm, 所以的五个圆(孔)及相邻两圆的间距之和为21-3=18(cm). d=[18-(3+2.8+2.6+2.4+2.2)]÷4=(cm). 29. (2011江苏南京,26,8分)如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s. ⑴当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由; ⑵已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值. A B C P Q O (第26题) 【答案】解:⑴直线与⊙P相切. 如图,过点P作PD⊥AB, 垂足为D. 在Rt△ABC中,∠ACB=90°,∵AC=6cm,BC=8cm, ∴.∵P为BC的中点,∴PB=4cm. ∵∠PDB=∠ACB=90°,∠PBD=∠ABC.∴△PBD∽△ABC. ∴,即,∴PD =2.4(cm) . 当时,(cm) ∴,即圆心到直线的距离等于⊙P的半径. ∴直线与⊙P相切. ⑵ ∠ACB=90°,∴AB为△ABC的外切圆的直径.∴. 连接OP.∵P为BC的中点,∴. ∵点P在⊙O内部,∴⊙P与⊙O只能内切. ∴或,∴=1或4. ∴⊙P与⊙O相切时,t的值为1或4. 30. (2011湖北黄石,24,9分)已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D。 (1)如图(8),若AC是⊙O2的直径,求证:AC=CD (2)如图(9),若C是⊙O1外一点,求证:O1C⊥AD (3)如图(10),若C是⊙O1内的一点,判断(2)中的结论是否成立。 【答案】(1)连接C O1,AB ∵AC是⊙O2的直径 ∴AB⊥BD,AD⊥C O1 ∴AD经过点O1 ∵AO1=DO1 ∴AC=CD (2)连接O1 O2,AO1 ∵O1 O2⊥AB ∴∠AO1O2+∠AG O1 ∵∠O1AB=∠C 又∵∠D=∠AO1B=∠AO1O2 ∴∠C+∠D=900 ∴O1C⊥AD (3)成立 31. (2011广东汕头,14,6分)如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿着x轴向右平稳4个长度单位得⊙P1. (1)画出⊙P1,并直接判断⊙P与⊙P1的位置关系; (2)设⊙P1与x轴正半轴,y轴正半轴的交点为A,B,求劣弧与弦AB围成的图形的面积(结果保留) 【答案】(1)如图所示,两圆外切; (2)劣弧的长度 劣弧和弦围成的图形的面积为 32. (2011浙江杭州,19, 6)在△ABC中,AB=,AC=,BC=1. (1)求证:∠A≠30°; (2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积. 【答案】(1)证明:在△ABC中,∵AB2=3,AC2+BC2=2+1=3,∴AC2+BC2=AB2,∴∠ACB=90°,∴,∴∠A≠30°. (2) 33. (2011 浙江湖州,20,8) 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2. (1) 求OE和CD的长; (2) 求图中阴影部分的面积. 【答案】解:(1)在△OCE中,∵∠CEO=90°,∠EOC=60°,OC=2,∴,∴,∵OA⊥CD,∴CE=DE,∴. (2) ∵,∴ 34. (2011浙江省,22,12分)如图,已知⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC,延长EC到P,连结PB,使PB=PE. (1) 在以下5个结论中:一定成立的是 (只需将结论的代号填入题中的横线上)①弧AC=弧BC;②OF=CF;③BF=AF;④AC2=AE•AB;⑤PB是⊙O的切线. (2) 若⊙O的半径为8cm,AE:EF=2:1,求弓形ACB的面积. 【答案】(1)①,③,④,⑤; (2)设EF=x,则AE=EC=PC=2x,PB=4x,且BF=3x,BE=4x, ∴PB=BE=PB ∴△PBE是等边三角形 ∴∠PBE=60º. ∵ EA=EC ∴∠CAE=∠ACE ∴∠PEB=∠CAE+∠ACE= 2∠CAE=∠BOC=60º. ∴∠BOA=120º ∴AB=错误!不能通过编辑域代码创建对象。, OF=4 ∵ 扇形OAB的面积=错误!不能通过编辑域代码创建对象。 △OAB的面积= 错误!不能通过编辑域代码创建对象。 ∴弓形ACB的面积=错误!不能通过编辑域代码创建对象。—错误!不能通过编辑域代码创建对象。. 35. (2011福建泉州,23,9分)如图,在中,,是边 (第23题) 上一点,以为圆心的半圆分别与、边相切于、两点,连接.已知,.求: (1); (2)图中两部分阴影面积的和. 【答案】解:(1)连接 ∵、分别切于、两点 ∴ 又∵ ∴四边形是矩形 ∵ ∴四边形是正方形. .................................(2分) ∴∥, ∴ ∴在中, ∴. .................................(5分) (2)如图,设与交于、两点.由(1)得,四边形是正方形 ∴ ∴ ∵在中,, ∴. .................................(7分) ∴ ∴ ∴图中两部分阴影面积的和为............ 9分 36. (2011湖南邵阳,23,8分)数学课堂上,徐老师出示了一道试题: 如图(十)所示,在正三角形ABC中,M是BC边(不含端点B,C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点,若∠AMN=60°,求证:AM=MN。 (1)经过思考,小明展示了一种正确的证明过程,请你将证明过程补充完整。 证明:在AB上截取EA=MC,连结EM,得△AEM。 ∵∠1=180°-∠AMB-∠AMN,∠2=180°-∠AMB -∠B,∠AMN=∠B=60°, ∴∠1=∠2. 又∵CN、平分∠ACP,∴∠4=∠ACP=60°。 ∴∠MCN=∠3+∠4=120°。………………① 又∵BA=BC,EA=MC,∴BA-EA=BC-MC,即BE=BM。 ∴△BEM为等边三角形,∴∠6=60°。 ∴∠5=10°-∠6=120°。………………② 由①②得∠MCN=∠5. 在△AEM和△MCN中, ∵__________,____________,___________, ∴△AEM≌△MCN(ASA)。 ∴AM=MN. (2)若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”(如图),N1是∠D1C1P1的平分线上一点,则当∠A1M1N1=90°时,结论A1M1=M1N1是否还成立?(直接给出答案,不需要证明) (3)若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”,请你猜想:当∠ AnMnNn=______°时,结论AnMn=MnNn仍然成立?(直接写出答案,不需要证明) 【答案】解:(1)∠5=∠MCN,AE=MC,∠2=∠1; (2)结论成立; (3)。 37. (2011江苏连云港,26,12分) 已知∠AOB=60º,半径为3cm的⊙P沿边OA从右向左平行移动,与边OA相切的切点记为点C. (1)⊙P移动到与边OB相切时(如图),切点为D,求劣弧的长; (2)⊙P移动到与边OB相交于点E,F,若EF=cm,求OC的长. 第26题 【答案】如图连结PD,PC,且PD⊥OB,PC⊥OA,∵∠AOB=60º,∴∠DPC=120º,由弧长公式可知. (2) 38. (2011福建福州,20,12分)如图9,在中,,是边上一点,以为圆心的半圆分别与、边相切于、两点,连接.已知,. 求:(1); (2)图中两部分阴影面积的和. 图9 【答案】解:(1)连接 ∵、分别切于、两点 ∴ 又∵ ∴四边形是矩形 ∵ ∴四边形是正方形 ∴∥, ∴ ∴在中, ∴ (2)如图,设⊙O与交于、两点.由(1)得,四边形是正方形 ∴ ∴ ∵在中,, ∴ ∴ ∴ ∴图中两部分阴影面积的和为 39. (2011福建福州,15,4分)以数轴上的原点为圆心,为半径的扇形中,圆心角 ,另一个扇形是以点为圆心,为半径,圆心角,点在数轴上表示实数,如图5.如果两个扇形的圆弧部分(和)相交,那么实数的取值范围是 图5 【答案】. 40.(2011湖南怀化,23,10分) 如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF. (1) 求证:OF∥BC; (2) 求证:△AFO≌△CEB; (3) 若EB=5cm,CD=cm,设OE=x,求x值及阴影部分的面积. 【答案】 解:(1)∵AB为⊙O的直径 ∴∠ACB=90° 又∵OF⊥AC于F,∴∠AFO=90°, ∴∠ACB=∠AFO ∴OF∥BC (2)由(1)知,∠CAB+∠ABC=90° 由已知AB⊥CD于E可得 ∠BEC=90°,∠CBE+∠ABC=90° ∴∠CBE=∠CAB 又∠AFO=∠BEC,BE=OF ∴△AFO≌△CEB (3)∵AB为⊙O的直径,CD是弦,AB⊥CD于E ∴∠OEC=90°,CE=CD= 在Rt△OCE中,设OE=x,OB=5+x=OC 由勾股定理得:OC2=OE2+EC2 ∴(5+x)2= 解得x=5. 在Rt△OCE中 tan∠COE= ∵∠COE为锐角 ∴∠OEC=60° 由圆的轴对称性可知阴影部分的面积为: 41. (2011广东省,14,6分)如图,在平面直角坐标系中,点P的坐标为(-4,0),⊙P的半径为2,将⊙P沿着x轴向右平稳4个长度单位得⊙P1. (1)画出⊙P1,并直接判断⊙P与⊙P1的位置关系; (2)设⊙P1与x轴正半轴,y轴正半轴的交点为A,B,求劣弧与弦AB围成的图形的面积(结果保留) 【答案】(1)如图所示,两圆外切; (2)劣弧的长度 劣弧和弦围成的图形的面积为 42. (2011山东临沂,23,9分)如图,以O为圆心的圆与△AOB的边AB相切于点C,与OB相交于点D,且OD=BD.已知sinA=,AC=. (1)求⊙O的半径; (2)求图中阴影部分的面积. 【解】(1)连接OC,设OC=r, ∵AC与⊙O相切, ∴OC⊥AC.………………………………………………………………………(1分) ∵sinA==, ∴OA=r,………………………………………………………………………(2分) ∴AC2=OA2-OC2 =r2-r2=21,……………………………………………………………………( 3分) ∴r=2,即⊙O的半径为2.………………………………………………………( 4分) (2)连接CD, ∵OD=BD,OC⊥BC, ∴CD=OD=OC,………………………………………………………………( 5分) ∴∠COD=60°,………………………………………………………………(6分) ∴BC=OC=2,………………………………………………………(7分) ∴S阴影=S△OCB-S扇形OCD =×2×2-π·22 =2-π.………………………………………………………………(9分) 43. (2011贵州贵阳,22,10分)[来源:www.shulihua.net] 在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E. (1)圆心O到CD的距离是______;(4分) (2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)(6分) (第22题图) 【答案】解:(1)连接OE. ∵CD切⊙O于点E, ∴OE⊥CD. 则OE的长度就是圆心O到CD的距离. ∵AB是⊙O的直径,OE是⊙O的半径, ∴OE=AB=5. 即圆心⊙到CD的距离是5. (2)过点A作AF⊥CD,垂足为F. ∵四边形ABCD是平行四边形, ∴∠B=∠D=60°,AB∥CD. ∵AB∥CD,OE⊥CD,AF⊥CD, ∴OA=OE=AF=EF=5. 在Rt△ADF中,∠D=60°,AF=5, ∴DF=, ∴DE=5+. 在直角梯形AOED中,OE=5,OA=5,DE=5+, ∴S梯形AOED=×(5+5+)×5=25+. ∵∠AOE=90°, ∴S扇形OAE=×π×52=π. ∴S阴影= S梯形AOED- S扇形OAE=25+-π. 即由弧AE、线段AD、DE所围成的阴影部分的面积为25+-π. 44. (2011湖北襄阳,23,7分) 如图7,在⊙O中,弦BC垂直于半径OA,垂足为E,D是优弧上一点,连接BD,AD,OC,∠ADB=30°. (1)求∠AOC的度数; (2)若弦BC=6cm,求图中阴影部分的面积. 图7 【答案】(1)∵弦BC垂直于半径OA, ∴BE=CE, = 1分 又∵∠ADB=30°,∴∠AOC=60°. 2分 (2)∵BC=6,∴. 在Rt△OCE中,. 3分 ∴ 4分 连接OB. ∵ = ∴∠BOC=2∠AOC=120° 5分 ∴S阴影=S扇形OBC-S△OBC == 6分 45. (2011山东东营,21,9分)(本题满分9分)如图,已知点A、B、C、D 均在已知圆上,AD∥BC,BD平分∠ABC,∠BAD=,四边形ABCD的周长为15. (1) 求此圆的半径; (2) 求图中阴影部分的面积。 【答案】解:(1)∵ AD∥BC,∠BAD=120°。∴∠ABC=60°。 又∵BD平分∠ABC ,∴∠ABD=∠DBC=∠ADB=30° ∴,∠BCD=60° ∴AB=AD=DC,∠BDC=90° 又在Rt△BDC中,BC是圆的直径,BC=2DC ∴BC+BC=15 ∴BC=6. ∴ 此圆的半径为3 (2)设BC的中点为O,由(1)可知O即为圆心,连接OA,OD,过O作OE⊥AD于E。在Rt△AOE中,∠AOE=30°。∴OE=OAcos30°= ∴ 46. (2011山东枣庄,23,8分)如图,点在的直径的延长线上,点在上,且AC=CD, ∠ACD=120°. (1)求证:是的切线; (2)若的半径为2,求图中阴影部分的面积. 【答案】(1)证明:连结. ∵ ,, ∴ .…………………………2分 ∵ ,∴ . ∴ . ∴ 是的切线. ………………………………………………………………4分 (2)解:∵∠A=30o, ∴ . ∴ π. ……………………………………………………6分 在Rt△OCD中, . ∴. ∴ 图中阴影部分的面积为π. …………………………………………8分 2010年全国各地中考数学压轴题汇编 第31章 与圆有关的解答题 1.(2010甘肃兰州)(本题满分6分)小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上. (1)(本小题满分4分)请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹). (2)(本小题满分2分))若△ABC中AB=8米,AC=6米,∠BAC=,试求小明家圆形花坛的面积. 【答案】(1)(本小题满分4分) 用尺规作出两边的垂直平分线 作出圆 ⊙O即为所求做的花园的位置.(图略) (2)(本小题满分2分) 解:∵∠BAC=,AB=8米,AC=6米, ∴BC=10米 ∴ △ABC外接圆的半径为5米 ∴小明家圆形花坛的面积为2平方米 . 2.(2010江苏南通)(本小题满分8分) 如图,⊙O的直径AB垂直于弦CD,垂足P是OB的中点, CD=6 cm,求直径AB的长. O B A D C · P (第20题) 【答案】方法一:连结OC,BC,则OC=OB ∵PC垂直平分OB,∴OC=BC.∴OC=OB=BC.∴△BOC为等边三角形. ∴∠BOC=60° 由垂径定理,CP=CD=3cm 在Rt△BOC中,=tan∠COP= ∴OP=cm. ∴AB=2OB=4OP=4cm. 方法二: 解:连OC,设OP为,则OC为2,直径AB为4, 在Rt△COP中, 即,解得 所以直径AB为cm. 3.(2010山东济宁)如图,为外接圆的直径,,垂足为点,的平分线交于点,连接,. (1) 求证:; (2) 请判断,,三点是否在以为圆心,以为半径的圆上?并说明理由. (第20题) 【答案】 (1)证明:∵为直径,, ∴.∴. 3分 (2)答:,,三点在以为圆心,以为半径的圆上. 4分 理由:由(1)知:,∴. ∵,,, ∴.∴. 6分 由(1)知:.∴. ∴,,三点在以为圆心,以为半径的圆上. 7分 4.(2010浙江嘉兴)如图,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个的顶点与点P重合,第二个的顶点是与PQ的交点,…,最后一个的顶点、在圆上. (第23题) (第23题 图1) (第23题 图2) (1)如图1,当时,求正三角形的边长; (2)如图2,当时,求正三角形的边长; (3)如题图,求正三角形的边长(用含n的代数式表示). 【答案】 (1)设与交于点D,连结, (第23题 图1) 则, 在中,, 即, 解得. …4分 (第23题 图2) (2)设与交于点E,连结, 则, 在中, 即, 解得. …4分 (第23题) (3)设与交于点F,连结, 则, 在中, 即, 解得. …4分 5.(2010 嵊州市)(10分) (1)请在图①的正方形ABCD内,画出使∠APB=90°的一个点P,并说明理由。 (2)请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,并说明理由。 (3)如图③,现在一块矩形钢板ABCD,AB=4,BC=3,工人师傅想用它裁出两块全等的、面积最大的△APB和△CPD钢板,且∠APB=∠CPD=60°,请你在图③中画出符合要求的点P和P。 图① 图② 图③ 【答案】(1)如图①,点P为所求 (2)如图②,圆上实线部分弧EF为所求②③ (3)如图③,点、为所求 6.(2010浙江金华)A C B D E F O 如图,AB是⊙O的直径,C是的中点,CE⊥AB于 E,BD交CE于点F. 1 2 (1)求证:CF﹦BF; (2)若CD ﹦6, AC ﹦8,则⊙O的半径为 ▲ , CE的长是 ▲ . 【答案】解:(1) 证明:∵AB是⊙O的直径,∴∠ACB﹦90° 又∵CE⊥AB, ∴∠CEB﹦90° ∴∠2﹦90°-∠A﹦∠1 又∵C是弧BD的中点,∴∠1﹦∠A ∴∠1﹦∠2, ∴ CF﹦BF﹒ A C B D E F O 1 2 (2) ⊙O的半径为5 , CE的长是 7.(2010 四川南充)如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE=BC. (1)求∠BAC的度数. (2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形. (3)若BD=6,CD=4,求AD的长. A F C D E G H B O A F C D E G H B O 【答案】(1)解:连结OB和OC. A F C D E G H B O ∵ OE⊥BC,∴ BE=CE. ∵ OE=BC,∴ ∠BOC=90°,∴ ∠BAC=45°. (2)证明:∵ AD⊥BC,∴ ∠ADB=∠ADC=90°. 由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°, ∠BAG=∠BAD,∠CAF=∠CAD, ∴ ∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°. ∴ ∠GAF=∠BAG+∠CAF+∠BAC=90°. ∴ 四边形AFHG是正方形. (3)解:由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4. 设AD的长为x,则 BH=GH-GB=x-6,CH=HF-CF=x-4. 在Rt△BCH中,BH2+CH2=BC2,∴ (x-6)2+(x-4)2=102. 解得,x1=12,x2=-2(不合题意,舍去). ∴ AD=12. 8.(2010福建福州)如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C. (1)求证:CB∥PD; (2)若BC=3,sinP=,求⊙O的直径. [来源:www.shulihua.net] (第19题) 【答案】解:(1)证明:∵ , ∴ ∠C=∠P. 第19题图 又∵ ∠1=∠C, ∴ ∠1=∠P. ∴ CB∥PD. (2)连接AC.[来源:www.shulihua.net] ∵ AB为0D的直径, ∴ ∠ACB=90°. 又∵ CD⊥AB, ∴ ∴ ∠A=∠P, ∴ sinA=sinP. 在Rt△ABC中, sinA=, ∵ sinP=, ∴ =.[来源:www.shulihua.netwww.shulihua.net] 又∵ BC=3, ∴ AB=5. 即⊙O的直径为5. 9.(2010邵阳)阅读下列材料,然后解答问题。 经过正四边形(即正方形)各顶点的圆叫作这个正四边形的外接圆。圆心是正四边形的对称中心,这个正四边形叫作这个圆的内接正四边形。 如图(十三),已知正四边形ABCD的外接圆⊙O,⊙O的面积为S,正四边形ABCD 的面积为S,以圆心O为顶点作∠MON,使∠MON=90°,将∠MON绕点O旋转,OM、ON分别与⊙O相交于点E、F,分别与正四边形ABCD的边相交于点G、H。设OE、OF、及正四边形ABCD的边围成的图形(图中阴影部分)的面积为S (1)当OM经过点A时(如图①),则S、S、S之间的关系为:S= (用含S、S的代数式表示); (2)当OM⊥AB时(如图②),点G为垂足,则(1)中的结论仍然成立吗?请说明理由。 (3)当∠MON旋转到任意位置时(如图③,)则(1)中的结论仍然成立吗?请说明理由. 图(十三) 【答案】解:(1) (2)成立。理由:连OB,可证图中的两个阴影部分的面积之和等于图①的阴影部分的面积 (3)成立。过点O分别作AB、BC的垂线交AB、BC于点P、Q,交圆于点X、Y,可证直角三角形OPG全等于直角三角形OQH,可说明两阴影部分面积之和等于图①的阴影部分面积. 10.(2010年上海)机器人“海宝”在某圆形区域表演“按指令行走”,如图5所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.(1)求弦BC的长;(2)求圆O的半径长. (本题参考数据:sin 67.4° = ,cos 67.4° = ,tan 67.4° = ) 图5 【答案】(1)过A作AH垂直NS于点H,∴∠AHO=90°, sin 67.4° = =, ∵OA=13米,∴AH=12米,∵AB∥OS,记BC与OS交于点D, ∴AH=BD=12米,∵OS⊥BC于点D,∴BD=CD=12米,∴BC=24米. (2)由(1)可得OH=5米,∵AB=14米,∴HD=9米,联接OB, ∵∠ODB=90°,∴OB= 11.(2010 广东珠海)如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连结PA、PB、PC、PD. (1)当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并证明; (2)若cos∠PCB=,求PA的长. 【答案】解:(1)当BD=AC=4时,△PAD是以AD为底边的等腰三角形 ∵P是优弧BAC的中点 ∴弧PB=弧PC ∴PB=PC ∵BD=AC=4 ∠PBD=∠PCA ∴△PBD≌△PCA ∴PA=PD 即△PAD是以AD为底边的等腰三角形 (2)由(1)可知,当BD=4时,PD=PA,AD=AB-BD=6-4=2 过点P作PE⊥AD于E,则AE=AD=1 ∵∠PCB=∠PAD ∴cos∠PAD=cos∠PCB= ∴PA= 12.(2010湖北荆门)如图,圆O的直径为5,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点. (1)求证:AC·CD=PC·BC; (2)当点P运动到AB弧中点时,求CD的长; (3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。 【答案】(1)由题意,AB是⊙O的直径;∴∠ACB=90。,∵CD⊥CP,∴∠PCD=90。 ∴∠ACP+∠BCD=∠PCB+∠DCB=90。,∴∠ACP=∠DCB,又∵∠CBP=∠D+∠DCB,∠CBP=∠ABP+∠ABC,∴∠ABC=∠APC,∴∠APC=∠D,∴△PCA∽△DCB;∴, 21世纪教育网 ∴AC·CD=PC·BC (2)当P运动到AB弧的中点时,连接AP,∵AB是⊙O的直径,∴∠APB=90。,又∵P是弧AB的中点,∴弧PA=弧PB,∴AP=BP,∴∠PAB=∠PBA=45.,又AB=5,∴PA=,过A作AM⊥CP,垂足为M,在Rt△AMC中,∠ACM=45 ,∴∠CAM=45,∴AM=CM=,在Rt△AMP中,AM2+AP2=PM2,∴PM=,∴PC=PM+=。由(1)知:AC·CD=PC·BC ,3×CD=PC×4,∴CD= (3)由(1)知:AC·CD=PC·BC,所以AC:BC=CP:CD;所以CP:CD=3:4,而△PCD的面积等于·=,CP是圆O的弦,当CP最长时,△PCD的面积最大,而此时CP就是圆O的直径;所以CP=5,∴3:4=5:CD;∴CD=,△PCD的面积等于·==; 13.(2010 四川成都)已知:如图,内接于⊙O,为直径,弦于,是AD的中点,连结并延长交的延长线于点,连结,分别交、于点、. (1)求证:是的外心; (2)若,求的长; (3)求证:. 【答案】(1)证明:∵C是AD的中点,∴AC=CD, ∴∠CAD=∠ABC⌒ ∵AB是⊙O的直径,∴∠ACB=90°。 ∴∠CAD+∠AQC=90° 又CE⊥AB,∴∠ABC+∠PCQ=90° ∴∠AQC=∠PCQ ⌒ ⌒ ∴在△PCQ中,PC=PQ, ⌒ ⌒ ∵CE⊥直径AB,∴AC=AE ∴AE=CD ∴∠CAD=∠ACE。 ∴在△APC中,有PA=PC, ∴PA=PC=PQ ∴P是△ACQ的外心。 (2)解:∵CE⊥直径AB于F, ∴在Rt△BCF中,由tan∠ABC=,CF=8, 得。 ∴由勾股定理,得 ∵AB是⊙O的直径, ∴在Rt△ACB中,由tan∠ABC=, 得。 易知Rt△ACB∽Rt△QCA,∴ ∴。 (3)证明:∵AB是⊙O的直径,∴∠ACB=90° ∴∠DAB+∠ABD=90° 又CF⊥AB,∴∠ABG+∠G=90° ∴∠DAB=∠G; ∴Rt△AFP∽Rt△GFB, ∴,即 易知Rt△ACF∽Rt△CBF, ∴ ∴ 由(1),知PC=PQ,∴FP+PQ=FP+PC=FC ∴。 14.(2010山东潍坊)如图,AB是⊙O的直径,C、D是⊙O上的两点,且AC=CD. (1)求证:OC∥BD; (2)若BC将四边形OBDC分成面积相等的两个三角形,试确定四边形OBDC的形状. 【答案】(1) ⊙O中,AC=CD,则∠ABC=∠DBC,∵OC=OB,则∠ABC=∠OAB,∴∠OCB=∠DBC,则OC∥BD; (2)∵OC∥BD,不妨设平行线OC与BD之间的距离为h,又S△OBC=OC×h,S△OBC=OC×h,∵BC将四边形OBDC分成面积相等的两个三角形,即S△OBC= S△DBC,则OC=BD,∴四边形OBDC为平行四边形,因为OC=OB,所以四边形OBDC为菱形. 15.(2010广东中山)如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4. (1)求∠POA的度数; (2)计算弦AB的长. 【答案】解:(1)∵PA与⊙O相切于A点, ∴∠PAO= 在RtΔPAO中,OA=2,OP=4 ∴∠POA= (2)∵AB⊥OP ∴AC=BC,∠OCA= 在RtΔAOC中,OA=2,∠AOC= ∴AC= ∴AB=2 16.(2010黑龙江哈尔滨)如图,AB、AC为⊙ O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C。 求证:CE=BF。 【答案】证明:∵OB、OC是⊙O的半径,∴OB=OC 又 ≌ ∴OE=OF ∴CE=BF 17.(2010四川 泸州)(本题满分10分)如图9,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC. (1) 求证:AE⊥DE; (2) 设以AD为直径的半圆交AB于F,连接DF交AE于G,已知CD=5,AE=8,求的值. 【答案】(1)证明:在平行四边形ABCD中,AB∥CD,∴∠BAD+∠ADC=180°, 又∵AE、DE平分∠BAD、∠ADC, ∴∠DAE+∠ADE=90°, ∴∠AED=90°, ∴AE⊥DE. (2)解:在平行四边形ABCD中,AD∥BC,AB=CD=5,AD=BC, ∴∠DAE=∠BEA, 又∵∠DAE=∠BAE,∴∠BEA=∠BAE, ∴BE=AB=5, 同理EC=CD=5, ∴AD=BC=BE+EC=10, 在RtAED中, DE===6, 又∵AD为半圆的直径,∴∠AFD=90°,∴∠AFD=∠AED, ∵∠DAE=∠FAG,∴AFG∽AED, ∴. 18.(2010吉林长春) 第16届亚运会将在中国广州举行。小李预定了两种价格的亚运会门票,其中甲种门票共花费280元,乙种门票共花费300元,甲种门票比乙种门票多2张,乙种门票价格是甲种门票价格的1.5倍,求甲种门票的价格。 【答案】 18.(2010吉林长春)如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm。求直尺的宽。 【答案】 19.(2010湖北宜昌)如图①,P是△ABC边AC上的动点,以P为顶点作矩形PDEF,顶点D,E在边BC上,顶点F在边AB上;△ABC的底边BC及BC上的高的长分别为a , h,且是关于x的一元二次方程的两个实数根,设过D, E,F三点的⊙O的面积为,矩形PDEF的面积为。 (1)求证:以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4; (2)求的最小值; (3)当的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m , n , k的取值是否有关?请说明理由。(11分) A C B (第23题) 解:解法一: (1)据题意,∵a+h=. ∴所求正方形与矩形的面积之比: 1分 由知同号, 2分 (说明:此处未得出只扣1分, 不再影响下面评分) 3分 即正方形与矩形的面积之比不小于4. (2)∵∠FED=90º,∴DF为⊙O的直径. ⊙ ∴⊙O的面积为:. 4分 矩形PDEF的面积:. ⊙ ∴面积之比: 设 ⊙ ……………………………………………………………6分 , ⊙ ,即时(EF=DE), 的最小值为 7分 ⊙ (3)当的值最小时,这时矩形PDEF的四边相等为正方形.[来源:www.shulihua.net] 过B点过BM⊥AQ,M为垂足,BM交直线PF于N点,设FP= e, ∵BN∥FE,NF∥BE,∴BN=EF,∴BN =FP =e. 由BC∥MQ,得:BM =AG =h. ∵AQ∥BC, PF∥BC, ∴AQ∥FP, ∴△FBP∽△ABQ. 8分 M N (说明:此处有多种相似关系可用,要同等分步骤评分) ∴,……9分 ∴.∴……10分 ……11分 ∴线段AQ的长与m,n,k的取值有关. (解题过程叙述基本清楚即可) 解法二: (1)∵a,h为线段长,即a,h都大于0, ∴ah>0…………1分(说明:此处未得出只扣1分,再不影响下面评分) ∵(a-h)2≥0,当a=h时等号成立. 故,(a-h)2=(a+h)2-4a h≥0. 2分 ∴(a+h)2≥4a h, ∴≥4.(﹡) 3分 这就证得≥4.(叙述基本明晰即可) (2)设矩形PDEF的边PD=x,DE=y,则⊙O的直径为 . S⊙O=…………4分, S矩形PDEF=xy ⊙ = = 6分 由(1)(*), . . ⊙ ∴的最小值是 7分 ⊙ (3)当的值最小时, 这时矩形PDEF的四边相等为正方形. ∴EF=PF.作AG⊥BC,G为垂足. ∵△AGB∽△FEB,∴.……8分 ∵△AQB∽△FPB, ,……9分 ∴=. 而 EF=PF,∴AG=AQ=h, ……………10分 ∴AG=h=, 或者AG=h= 11分 ∴线段AQ的长与m,n,k的取值有关. 20.(2010福建省南平)如图,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积. · 第21题 A B C O D 【答案】解:∵AB是直径, ∴∠ACB=∠ADB=90°, 在Rt△ABC中,AB=6, AC= 2,∴BC=== 4 ∵∠ACB的平分线交⊙O于点D,∴∠DAC=∠BCD ∴=, ∴AD=BD ∴在Rt△ABD中,AD=BD= AB=3 ∴四边形ADBC的面积=S△ABC+S△ABD=AC·BC+AD·BD =×2×4+×(3)2 =9+4 21.(2010广西河池)如图10,为的直径,为弦,且,垂足为. (1)如果的半径为4,,求的度数; (2)若点为的中点,连结,.求证:平分; (3)在(1)的条件下,圆周上到直线距离为3的点有多少个?并说明理由. A B D E O C H 【答案】解:(1)∵ AB为⊙O的直径,CD⊥AB ∴ CH=CD=2 A B D E O C H 在Rt△COH中,sin∠COH== ∴ ∠COH=60° ∵ OA=OC ∴∠BAC=∠COH=30° (2)∵ 点E是的中点 ∴OE⊥AB ∴ OE∥CD ∴ ∠ECD=∠OEC 又∵ ∠OEC=∠OCE ∴ ∠OCE=∠DCE ∴ CE平分∠OCD (3)圆周上到直线的距离为3的点有2个. 因为劣弧上的点到直线的最大距离为2, 上的点到直线AC的最大距离为6,,根据圆的轴对称性,到直线AC距离为3的点有2个. 22.(2010广东清远)如下图,在⊙O中,点P在直径AB上运动,但与A、B两点不重合,过点P作弦CE⊥AB,在上任取一点D,直线CD与直线AB交于点F,弦DE交直线AB于点M,连接CM. (1)如图10,当点P运动到与O点重合时,求∠FDM的度数. 图10 图11 图12 C A B (P) E O M F D C A B P E O F D M O C A B P E F D M (2)如图11、图12,当点P运动到与O点不重合时,求证:FM·OB=DF·MC. 【答案】28. 解:(1)点P与点O重合时,(如图10) ∵CE是直径,∴∠CDE=90°.…………(1分) ∵∠CDE+∠FDM=180°,∴∠FDM=90°.…………(2分) (2)当点P在OA上运动时(如图11) ∵OP⊥CE,∴==,CP=EP. ∴CM=EM. ∴∠CMP=∠EMP. ∵∠DMO=∠EMP, ∴∠CMP=∠DMO. ∵∠CMP+∠DMC=∠DMO+∠DMC, ∴∠DMF=∠CMO. …………(3分) ∵∠D所对的弧是,∠COM所对的弧是, ∴∠D=∠COM. …………(4分) ∴△DFM∽△OCM. ∴= ∴FM·OC=DF·MC. ∵OB=OC, ∴FM·OB=DF·MC. …………(5分) 当点P在OB上运动时,(如图12) 证法一:连结AC,AE. ∵OP⊥CE,∴==,CP=EP. ∴CM=EM, ∴∠CMO=∠EMO. ∵∠DMF=∠EMO, ∴∠DMF=∠CMO.………………(6分) ∵∠CDE所对的弧是,∠CAE所对的弧是. ∴∠CDE+∠CAE=180°. ∴∠CDM+∠FDM=180°,∴∠FDM=∠CAE. ∵∠CAE所对的弧是,∠COM所对的弧是, ∴∠CAE=∠COM. ∴∠FDM=∠COM. ………………(7分) ∴△DFM∽△OCM. ∴=. ∴FM·OC=DF·MC. ∵OB=OC, ∴FM·OB=DF·MC. ………………(8分) 证法二:∵OP⊥CE, ∴==,==,CP=EP. ∴CM=EM, ∴∠CMO=∠EMO. ∵∠DMF=∠EMO, ∴∠DMF=∠CMO.………………(6分) ∵∠CDE所对的弧是, ∴∠CDE=度数的一半=的度数=180°-的度数. ∴∠FDM=180°-∠CDE=180°-(180°-的度数)=的度数. ∵∠COM=的度数. ∴∠FDM=∠COM. ………………(7分) ∴△DFM∽△OCM. ∴=. ∴FM·OC=DF·MC. ∵OB=OC, ∴FM·OB=DF·MC. ………………(8分) 23.(2010湖北恩施自治州)(1)计算:如图①,直径为的三等圆⊙O、⊙O、⊙O两两外切,切点分别为A、B、C ,求OA的长(用含的代数式表示). 21世纪教育网 (2)探索:若干个直径为的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中层圆圈的高度和(用含、的代数式表示). (3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米.用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?(≈1.73) 【答案】解(1)∵⊙O、⊙O、⊙O两两外切, ∴OO=OO=OO=a 又∵OA= OA ∴OA⊥OO ∴OA= = (2) = =, 方案二装运钢管最多。即:按图10③的方式排放钢管,放置根数最多. 根据题意,第一层排放31根,第二层排放30根,…… 设钢管的放置层数为n,可得 解得 ∵ 为正整数 ∴=35 钢管放置的最多根数为:31×18+30×17=1068(根) 24.(2010湖北十堰)(本小题满分9分)如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C. (1)求证:O2C⊥O1O2; (2)证明:AB·BC=2O2B·BO1; (3)如果AB·BC=12,O2C=4,求AO1的长. O1 O2 A B C 【答案】解:(1)∵AO1是⊙O2的切线,∴O1A⊥AO2 ∴∠O2AB+∠BAO1=90° 又O2A=O2C,O1A=O1B,∴∠O2CB=∠O2AB,∠O2BC=∠ABO1=∠BAO1 ∴∠O2CB+∠O2BC=∠O2AB+∠BAO1=90°,∴O2C⊥O2B,即O2C⊥O1O2 O1 O2 A B C D (2)延长O2O1交⊙O1于点D,连结AD. ∵BD是⊙O1直径,∴∠BAD=90° 又由(1)可知∠BO2C=90° ∴∠BAD=∠BO2C,又∠ABD=∠O2BC ∴△O2BC∽△ABD ∴ ∴AB·BC=O2B·BD 又BD=2BO1 ∴AB·BC=2O2B·BO1 (3)由(2)证可知∠D=∠C=∠O2AB,即∠D=∠O2AB,又∠AO2B=∠DO2A ∴△AO2B∽△DO2A ∴ ∴AO22=O2B·O2D ∵O2C=O2A ∴O2C2=O2B·O2D ① 又由(2)AB·BC=O2B·BD ② 由①-②得,O2C2-AB·BC= O2B2 即42-12=O1B2 ∴O2B=2,又O2B·BD=AB·BC=12 ∴BD=6,∴2AO1=BD=6 ∴AO1=3 25.(2010湖北黄石)在△ABC中,分别以AB、BC为直径⊙O、⊙O,交于另一点D. ⑴证明:交点D必在AC上; ⑵如图甲,当⊙O与⊙O半径之比为4︰3,且DO与⊙O相切时,判断△ABC的形状,并求tan∠ODB的值; ⑶如图乙,当⊙O经过点O,AB、DO的延长线交于E,且BE=BD时,求∠A的度数. 【答案】查看更多