- 2021-05-10 发布 |
- 37.5 KB |
- 7页
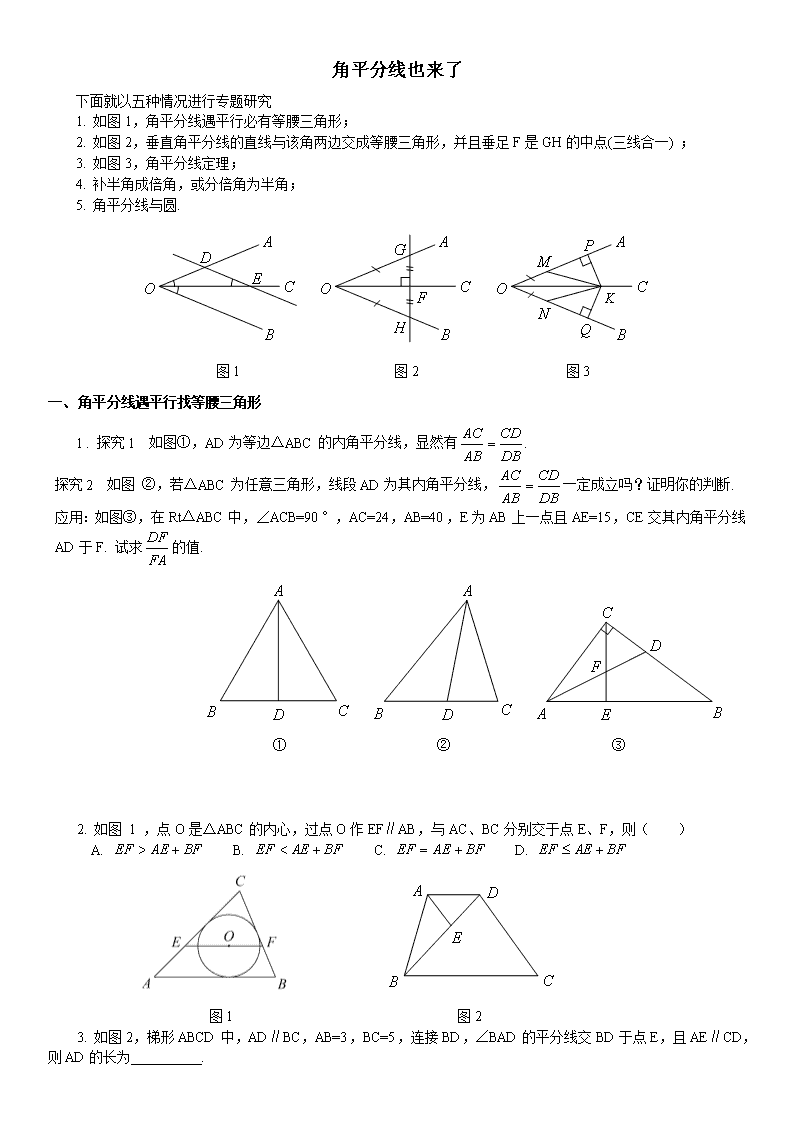
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017数学中考专题5角平分线问题
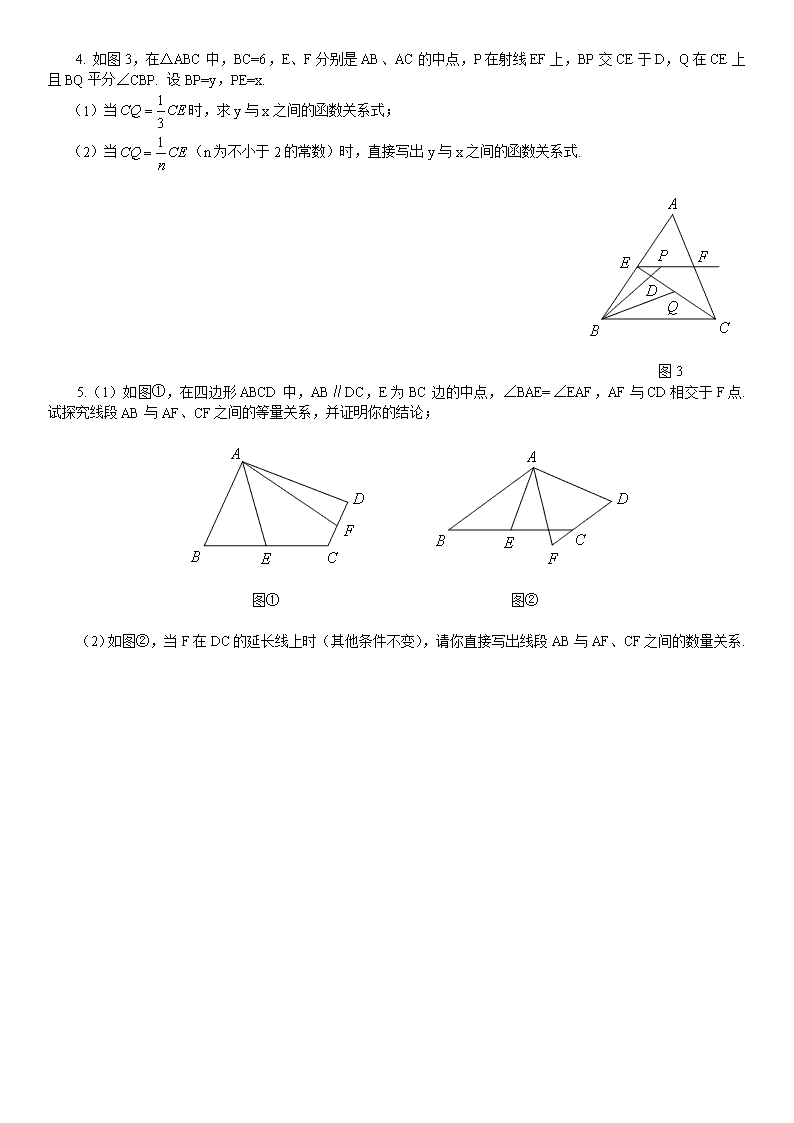
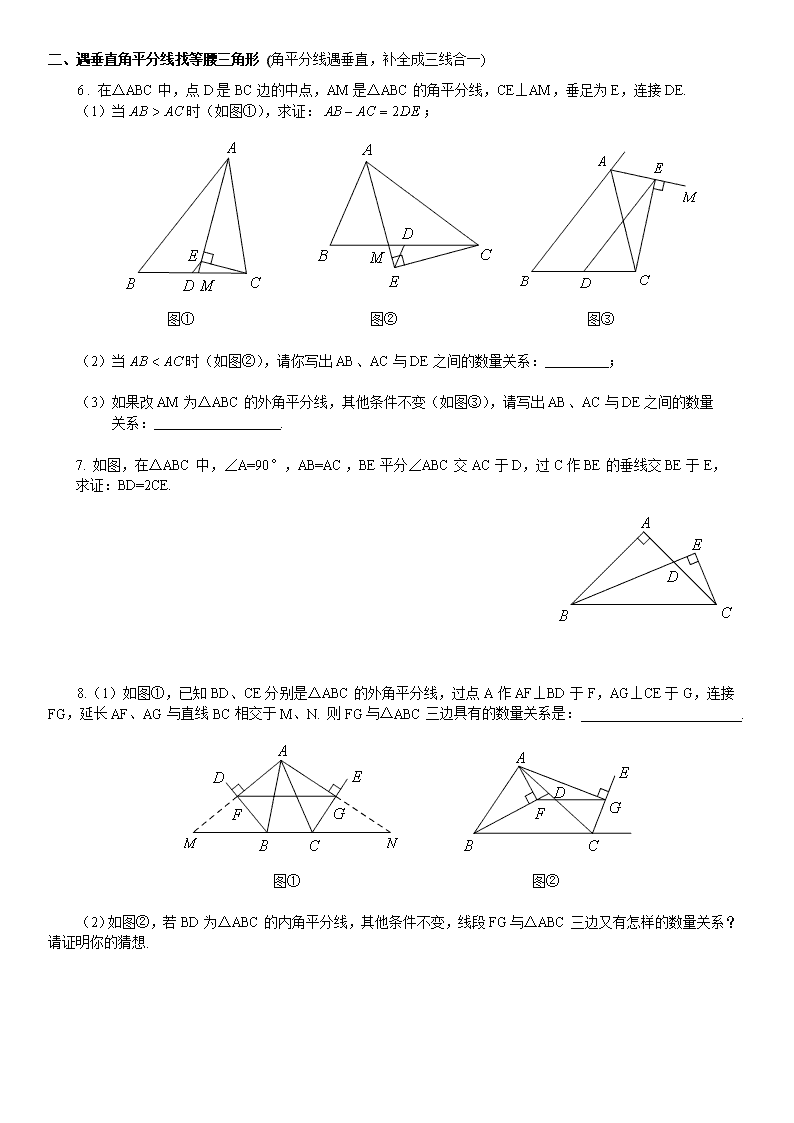
角平分线也来了 下面就以五种情况进行专题研究 1. 如图1,角平分线遇平行必有等腰三角形; 2. 如图2,垂直角平分线的直线与该角两边交成等腰三角形,并且垂足F是GH的中点(三线合一) ; 3. 如图3,角平分线定理; 4. 补半角成倍角,或分倍角为半角; 5. 角平分线与圆. 图1 图2 图3 一、 角平分线遇平行找等腰三角形 1 . 探究1 如图①,AD为等边△ABC的内角平分线,显然有. 探究2 如图 ②,若△ABC为任意三角形,线段AD为其内角平分线,一定成立吗?证明你的判断. 应用:如图③,在Rt△ABC中,∠ACB=90°,AC=24,AB=40,E为AB上一点且AE=15,CE交其内角平分线AD于F. 试求的值. ① ② ③ 2. 如图 1 ,点O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交于点E、F,则( ) A. B. C. D. 图1 图2 3. 如图2,梯形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线交BD于点E,且AE∥CD,则AD的长为 . 4. 如图3,在△ABC中,BC=6,E、F分别是AB、AC的中点,P在射线EF上,BP交CE于D,Q在CE上且BQ平分∠CBP. 设BP=y,PE=x. (1)当时,求y与x之间的函数关系式; (2)当(n为不小于2的常数)时,直接写出y与x之间的函数关系式. 图3 5.(1)如图①,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与CD相交于F点. 试探究线段AB与AF、CF之间的等量关系,并证明你的结论; 图① 图② (2)如图②,当F在DC的延长线上时(其他条件不变),请你直接写出线段AB与AF、CF之间的数量关系. 二、遇垂直角平分线找等腰三角形 (角平分线遇垂直,补全成三线合一) 6 . 在△ABC中,点D是BC边的中点,AM是△ABC的角平分线,CE⊥AM,垂足为E,连接DE. (1)当时(如图①),求证:; 图① 图② 图③ (2)当时(如图②),请你写出AB、AC与DE之间的数量关系: ; (3)如果改AM为△ABC的外角平分线,其他条件不变(如图③),请写出AB、AC与DE之间的数量 关系: . 7. 如图,在△ABC中,∠A=90°,AB=AC,BE平分∠ABC交AC于D,过C作BE的垂线交BE于E, 求证:BD=2CE. 8.(1)如图①,已知BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD于F,AG⊥CE于G,连接FG,延长AF、AG与直线BC相交于M、N. 则FG与△ABC三边具有的数量关系是: . 图① 图② (2)如图②,若BD为△ABC的内角平分线,其他条件不变,线段FG与△ABC三边又有怎样的数量关系?请证明你的猜想. 三、遇倍角或半角 见半角补成倍角或等分倍角;见倍角等分之或造半角的等腰三角形 14 . 在△ABC中,∠A=90°,点D在线段BC上,∠C=2∠EDB,BE⊥DE于E,DE交AB于点F. (1)如图①,当AB=AC时,1)∠EBF= ;2)探究线段BE与FD的数量关系,并加以证明; (2)如图②,当AB=k AC时,求的值(用含k的式子表示). 图① 图② 15 . 阅读材料:如图①,在△ABC中,∠A=2∠B,且∠A=60°. 小明通过以下计算: 由题意知∠B=30°,∠C=90°,,,得:,即. 于是小明猜想:对于任意的△ABC,当∠A=2∠B时,关系式都成立. 图① 图 ② 图③ (1)如图 ②,请你用等腰Rt△进行验证,判断小明的猜测是否正确,并写出验证过程; (2)如图③,你认为小明的猜想是否正确,若认为正确,请你证明;否则,请说明理由; (3)若某三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长. 四、见角平分线用性质(角关于角平分线所在直线对称,依角的对称性找(或造)全等) 16 . 如图1,在△ABC中,三角形的外角∠DAC和∠ACF的平分线交于点E. (1)当∠B=47°,则∠AEC= ;(2)当∠B=α时,∠AEC= . 图1 图2 图3 17 . 如图2,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N. 有下列四个结论:① DF=CF;② BF⊥EN;③ △BEN是等边三角形;④ S△BEF=3S△DEF. 其中,结论正确的是 (填序号) 18 . 如图3,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An. 设∠A=θ. 则(1)∠A1= ;(2)∠An= . 19 . 已知,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA、NB分别相交于点D、E. (1)如图①,当直线l与直线MA垂直时,线段AD、BE、AB满足怎样的数量关系,请证明之; 图① 图 ② (2)如图②,当直线l与直线MA不垂直且交点D、E都在AB的同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由. 五、两角平分线相交用内切圆 三角形内切圆是其三个内角平分线的交点,在Rt△中,内切圆半径r与三边a、b、c()的关系为. 20 . 如图1,已知Rt△ABC中,AC=24,斜边AB=25,半径为1的⊙P在△ABC内部沿顺时针方向滚动,且运动过程中⊙P一直保持与△ABC的边相切,当 P第一次回到它的初始位置时所经过路径的长度是( ) A. B. 25 C. D. 56 图1 图2 21 . 如图2,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F. 求证:查看更多