- 2021-05-10 发布 |
- 37.5 KB |
- 28页


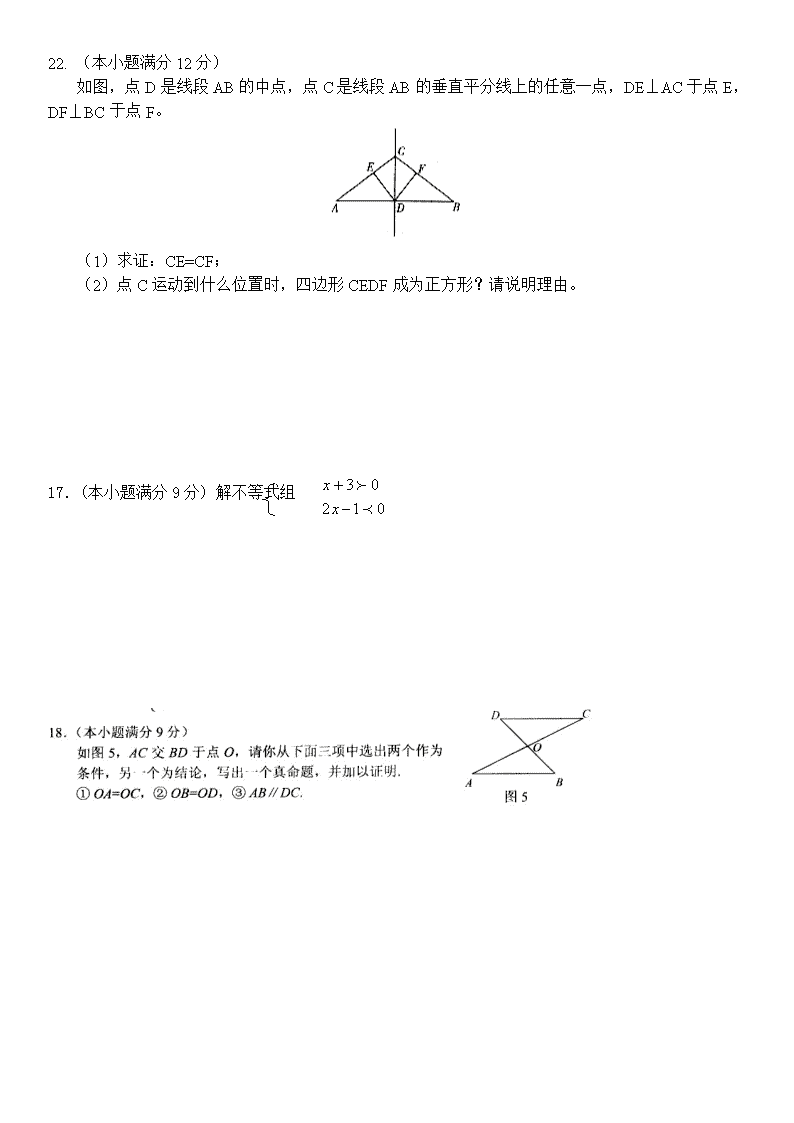
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2005中考数学1622题专练
17. (本小题满分9分) 计算: 18. (本小题满分9分) 如图,AB是圆O的弦,直线DE切圆O于点C,AC=BC, 求证:DE//AB。 19. (本小题满分10分) 解方程组: 20. (本小题满分10分) 以上统计图中数据来源于2004年12月广州市教育局颁布的《广州市2004/2005学年教育事业统计简报》。其中,小学按6年制,初中、高中均按3年制统计。 (1)请回答,截止2004年底,广州市在校小学生、在校初中生平均每个年级的人数哪一个更多?多多少? (2)根据该统计图,你还能得到什么信息?请你写出两条不同于(1)的解答的信息。 21. (本小题满分12分) 某次知识竞赛共有20道选择题。对于每一道题,若答对了,则得10分;若答错了或不答,则扣3分。请问至少要答对几道题,总得分才不少于70分? 22. (本小题满分12分) 如图,点D是线段AB的中点,点C是线段AB的垂直平分线上的任意一点,DE⊥AC于点E,DF⊥BC于点F。 (1)求证:CE=CF; (2)点C运动到什么位置时,四边形CEDF成为正方形?请说明理由。 17.(本小题满分9分) 解不等式组 19.(本小题满分lO分) 广州市某中学高一(6)班共54名学生,经调查其中40名学生患有不同程度的近视眼病,初患近视眼病的各个年龄段频数分布如下: 初患近视眼病年龄 2岁~5岁 5岁~8岁 8岁~11岁 11岁~14岁 14岁~17岁 频数(人数) 3 4 13 a 6 (注:表中2岁~5岁的意义为大于等于2岁并且小于5岁,其它类似) (1)求a的值,并把下面的频数分布直方图补充画完整; (2)从上研的直方图中你能得出什么结论(只限写出一个结论)?你认为此结论反映了教育与社会的什么问题? 20.(本小题满分10分) 如图6,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游 戏(当指针指在边界线上时视为无效,重转). (1)小夏说:“如果两个指针所指区域内的数之和为6或7, 则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性肚分别是多少? (2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性. 21.(本小题满分12分) 目前广州市小学和初中在任校生共有约128万人,其中小学生在校人数比初中生在校人 数的2倍多14万人(数据来源:2005学年度广州市教育统计手册). (1)求目前广州市在校的小学生人数和初中生人数; (2)假设今年小学生每人需交杂费500元,初中生每人需交杂费1000元,而这些费用全部由广州市政府拨款解决,则广州市政府要为此拨款多少? 22.(本小题满分12分) 如图7⊙0的半径为1,过点A(2,0)的直线切⊙0于点B,交y轴于点C. (1)求线段AB的长; (2)求以直线AC为图象的一次函数的解析式. 17、(9分)请以下列三个代数式中任选两个构造一个分式,并化简该分式。 18、(9分)下图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的体积。(结果保留) 19、(10分)甲、乙、丙三名学生各自随机选择到A、B两个书店购书, (1)求甲、乙两名学生在不同书店购书的概率; (2)求甲、乙、丙三名学生在同一书店购书的概率。 20、(10分)某校初三(1)班50名学生参加1分钟跳绳体育考试。1分钟跳绳次数与频数经统计后绘制出下面的频数分布表(60~70表示为大于等于60并且小于70)和扇形统计图。 (1)求m、n的值; (2)求该班1分钟跳绳成绩在80分以上(含80分)的人数占全班人数的百分比; (3)根据频数分布表估计该班学生1分钟跳绳的平均分大约是多少?并说明理由。 21、(12分)如图,在△ABC中,AB=AC,内切圆O与边BC、AC、AB分别切于D、E、F. (1)求证:BF=CE; (2)若∠C=30°,,求AC. 22、(14分)二次函数图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC. (1)求C的坐标; (2)求二次函数的解析式,并求出函数最大值。 17、 (9分)分解因式 18、 (9分)小青在九年级上学期的数学成绩如下表所示 测验类别 平时 期中 考试 期末 考试 测验1 测验2 测验3 课题学习 成绩 88 70 98 86 90 87 (1)计算该学期的平时平均成绩; (2)如果学期的总评成绩是根据图5所示的权重计算, 图5 请计算出小青该学期的总评成绩。 19、 (10分)如图6,实数、在数轴上的位置, 化简 图6 20、 (10分)如图7,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC且与AB的延长线交于点E,求证:四边形AECD是等腰梯形 图7 21、 (12分)如图8,一次函数的图象与反比例函数的图象相交于A、B两点 (1)根据图象,分别写出A、B的坐标; (2)求出两函数解析式; (3)根据图象回答:当为何值时, 一次函数的函数值大于反比例函数的函数值 22、 (12分)2008年初我国南方发生雪灾,某地电线被雪压断,供电局的维修队要到30千米远的郊区进行抢修。维修工骑摩托车先走,15分钟后,抢修车装载所需材料出发,结果两车同时到达抢修点。已知抢修车的速度是摩托车速度的1.5倍,求两种车的速度。 17. (本小题满分9分) 如图9,在ΔABC中,D、E、F分别为边AB、BC、CA的中点。 证明:四边形DECF是平行四边形。 18. (本小题满分10分) 解方程 19.(本小题满分10分) 先化简,再求值:,其中 20.(本小题满分10分) 如图10,在⊙O中,∠ACB=∠BDC=60°,AC=, (1)求∠BAC的度数; (2)求⊙O的周长 21. (本小题满分12分) 有红、白、蓝三种颜色的小球各一个,它们除颜色外没有其它任何区别。现将3个小球放入编号为①、②、③的三个盒子里,规定每个盒子里放一个,且只能放一个小球。 (1)请用树状图或其它适当的形式列举出3个小球放入盒子的所有可能情况; (2)求红球恰好被放入②号盒子的概率。 22. (本小题满分12分) 如图11,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点,且点M的坐标是(1,2)。 (1)写出点A、B的坐标; (2)求直线MN所对应的函数关系式; (3)利用尺规作出线段AB关于直线MN的对称图形(保留作图痕迹,不写作法)。 17.(9分)解不等式组 18. (9分)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF。 A D F E B C 求证:△ACE≌△ACF 19. (10分)分解因式:8(x2-2y2)-x(7x+y)+xy 正面 20. (10分)5个棱长为1的正方体组成如图的几何体。 (1)该几何体的体积是_________(立方单位) 表面积是_________(平方单位) (2)画出该几何体的主视图和左视图。 21.(12分)某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠。已知小敏5月1日前不是该商店的会员。 (1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元? (2)请帮小敏算一算,所购买商品的价格在什么范围时,采用方案一更合算? 22.(12分)某中学九年级(3)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题: (1)求a的值; (2)用列举法求以下事件的概率:从上网时间在6~10小时的5名学生中随机选取2人,其中至少有1人的上网时间在8~10小时。 17.(本小题满分9分) 解方程:. 18.(本小题满分9分) 如图8,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长. 19.(本小题满分10分) 先化简,再求值:,其中 20.(本小题满分10分) 已知四边形ABCD是平行四边形(如图9),把△ABD沿对角线BD翻折180°得到△AˊBD. (1) 利用尺规作出△AˊBD.(要求保留作图痕迹,不写作法); (2)设D Aˊ 与BC交于点E,求证:△BAˊE≌△DCE. 21.(本小题满分12分) 在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下: 11 10 6 15 9 16 13 12 0 8 2 8 10 17 6 13 7 5 7 3 12 10 7 11 3 6 8 14 15 12 (1) 求样本数据中为A级的频率; (2) 试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数; (3) 从样本数据为C级的人中随机抽取2人,用列举法求抽得2个人的“日均发微博条数”都是3的概率. 22.(本小题满分12分) 如图10, 在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里. (1) 求船P到海岸线MN的距离(精确到0.1海里); (2) 若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处. 17.(本小题满分9分) 解不等式:,并在数轴上表示解集. 18.(本小题满分9分) 如图,的对角线、相交于点,过点且与、分别交于点、,求证:. 19.(本小题满分10分) 已知多项式 (1)化简多项式; (2)若,求的值. 20.(本小题满分10分) 某校初三(1)班名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下: (1)求的值; (2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数; (3)在选报“推铅球”的学生中,有名男生,名女生.为了了解学生的训练效果,从这 名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率. 21.(本小题满分12分) 已知一次函数的图象与反比例函数的图象交于两点,点的横坐标为. (1)求的值和点的坐标; (2)判断点所在的象限,并说明理由.[来源:Z§xx§k.Com] 22.(本小题满分12分) 从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是千米,普通列车的行驶路程是高铁的行驶路程的倍. (1)求普通列车的行驶路程; (2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短小时,求高铁的平均速度. 17.(本小题满分9分) 解方程:. 18.(本小题满分9分) 如图7,正方形ABCD中,点E、F分别在AD,CD上,且AE=DF,连接BE,AF. 求证:BE=AF. 19.(本小题满分10分) 已知.[来源:学科网ZXXK] (1)化简A; (2)当满足不等式组,且为整数时,求A的值. 20.(本小题满分10分) 已知反比例函数的图象的一支位于第一象限. (1)判断该函数图象的另一支所在的象限,并求的取值范围; (2)如图8,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于轴 对称,若的面积为6,求的值. 21.(本小题满分12分) 某地区2013年投入教育经费2500万元,2015年投入教育经费3025万元. (1)求2013年至2015年该地区投入教育经费的年平均增长率; (2)根据(1)所得的年平均增长率,预计2016年该地区将投入教育经费多少万元. 22.(本小题满分12分) 4件同型号的产品中,有1件不合格品和3件合格品. (1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;[来源:Z#xx#k.Com] (2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率; (3)在这4件产品中加入件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验.通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出的值大约是多少? 17. (9分)(2016•广州)解不等式组并在数轴上表示解集. 18.(9分)(2016•广州)如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数. 19.(10分)(2016•广州)某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为个小组打,各项成绩均按百分制记录.甲、乙、丙三个小组各项得分如表: 小组 研究报告 小组展示 答辩 甲 91 80 78 乙 81 74 85 丙 79 83 90 (1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序; (2)如果按照研究报告占40%,小组展示占30%,答辩占30%计算各小组的成绩,哪个小组的成绩最高? 20.(10分)(2016•广州)已知A=(a,b≠0且a≠b) (1)化简A; (2)若点P(a,b)在反比例函数y=﹣的图象上,求A的值. 21.(12分)(2016•广州)如图,利用尺规,在△ABC的边AC上方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD∥AB(尺规作图要求保留作图痕迹,不写作法) 22.(12分)(2016•广州)如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30m到达A′处, (1)求A,B之间的距离; (2)求从无人机A′上看目标D的俯角的正切值.查看更多