山东济宁市中考数学试题及答案
济宁市2011年高中阶段学校招生考试
数学试题
第Ⅰ卷 (选择题 30分)
一、选择题(下列各题的四个选项中,只有一项符合题意,每小题3分,共30分)。
1、计算-1-2的结果是
A.-1 B.1 C.-3 D. 3
2、下列等式成立的是
A.a2+a3=a5 B.a3-a2=a C.a2.a3=a6 D.(a2)3=a6
3、如果一个等腰三角形的两边长分别是5cm和6cm,那么此三角形的周长是
A.15cm B.16cm C.17cm D. 16cm或17cm
4、下列各式计算正确的是
A. B.
C. D.
5、已知关于x的方程x2+bx+a=0的一个根是-a(a≠0),则a-b值为
21
1
C
B
A
D
E
第6题
A.-1 B.0 C.1 D.2
6、如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是
A.10° B. 20° C.30° D. 40°
7、在x2□2xy□y2的空格□中,分别填上“+”或“-”,在所得的代数式中,能构成完全平方式的概率是
A. 1 B. C. D.
8、已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
x
…
0
1
2
3
4
…
y
…
4
1
0
1
4
…
E
D
C
A
B
第9题
点A(x1,y1)、B(x2,y2)在函数的图象上,则当1
y2 B. y1 < y2 C. y1 ≥ y2 D. y1 ≤ y2
9、如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是
A. 22cm B.20cm C. 18cm D.15cm
10、如图,是某几何体的三视图及相关数据,则下面判断正确的是
A. a>c B. b>c C. a2+4b2=c2 D. a2+b2=c2
第Ⅱ卷 (非选择题 70分)
二、 填空题(每小题3分,共15分;只要求填写最后结果)
11、反比例函数 的图象在第一、三象限,则m的取值范围是 。
12、将二次函数y=x2-4x+5化成 y=(x-h)2+k的形式,则y= 。
13、如图,在Rt△ABC中,∠C=90°,BC=4cm,以点C为圆心,以3cm长为半径作圆,则⊙C与AB的位置关系是 。
14、如图,观察每一个图中黑色正六边形的排列规律,则第10个图中黑色正六边形有 个。
第13题
A
C
B
第15题
G
D
B
E
C
A
F
15、如图,等边三角形ABC中,D、E分别为AB、BC边上的两动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G ,则 。
三、 解答题(共55分,解答应写出文字说明、证明过程或推演步骤)
16、(5分)计算:
B
A
O
第17题
E
D
C
F
17、(5分)如图,在平行四边形ABCD中,对角线AC、BD相交于O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F,求证:四边形BEDF是菱形。
67.5°
36.9°
A
P
B
第18题
18、(6分)日本福岛出现核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场监测与海水采样,针对核泄漏在极端情况下对海洋环境的影响及时开展分析评估。如图,上午9时,海检船位于A处,观测到某港口城市P位于海检船的北偏西67.5°方向,海检船以21海里/时 的速度向正北方向行驶,下午2时海检船到达B处,这时观察到城市P位于海检船的南偏西36.9°方向,求此时海检船所在B处与城市P的距离?
(参考数据:
,,,)
19、
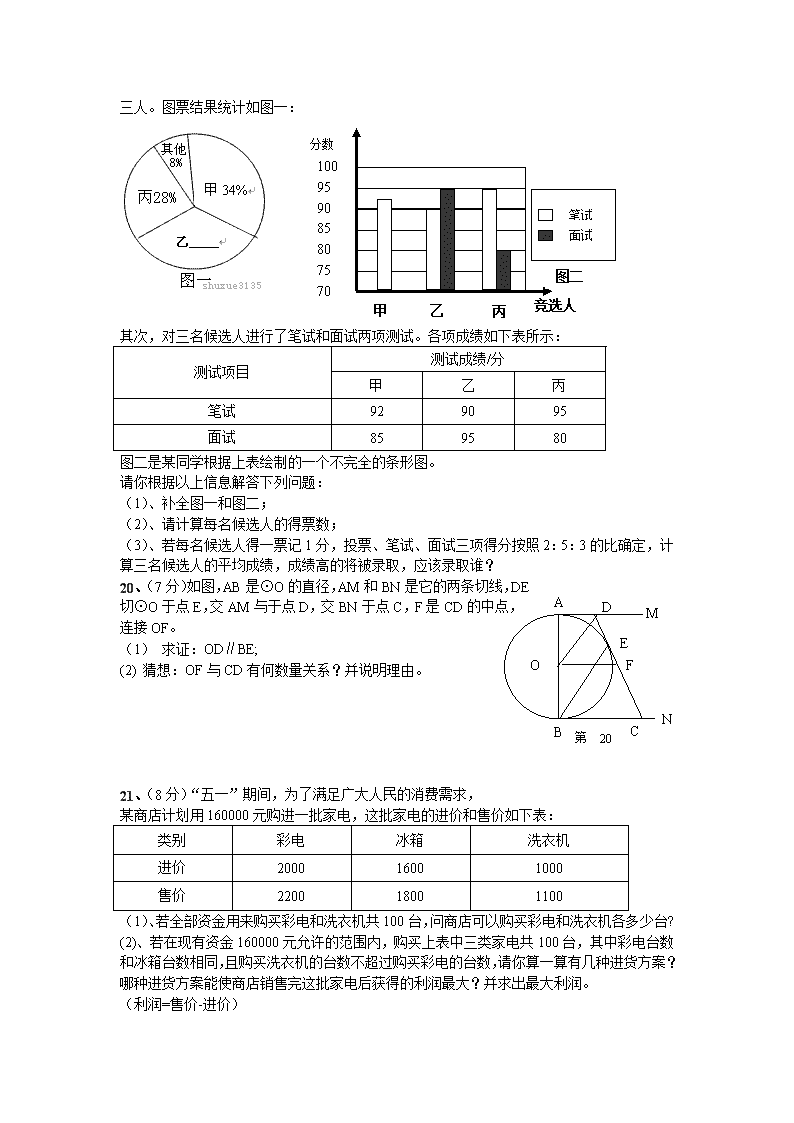
(6分)某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人。图票结果统计如图一:
甲
乙
丙
竞选人
100
95
90
85
80
75
70
分数
笔试
面试
图二
其次,对三名候选人进行了笔试和面试两项测试。各项成绩如下表所示:
测试项目
测试成绩/分
甲
乙
丙
笔试
92
90
95
面试
85
95
80
图二是某同学根据上表绘制的一个不完全的条形图。
请你根据以上信息解答下列问题:
(1)、补全图一和图二;
(2)、请计算每名候选人的得票数;
(3)、若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
A
第20题
N
C
B
D
E
F
M
O
O
20、(7分)如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM与于点D,交BN于点C,F是CD的中点,连接OF。
(1) 求证:OD∥BE;
(2) 猜想:OF与CD有何数量关系?并说明理由。
21、(8分)“五一”期间,为了满足广大人民的消费需求,
某商店计划用160000元购进一批家电,这批家电的进价和售价如下表:
类别
彩电
冰箱
洗衣机
进价
2000
1600
1000
售价
2200
1800
1100
(1)、若全部资金用来购买彩电和洗衣机共100台,问商店可以购买彩电和洗衣机各多少台?
(2)、若在现有资金160000元允许的范围内,购买上表中三类家电共100台,其中彩电台数和冰箱台数相同,且购买洗衣机的台数不超过购买彩电的台数,请你算一算有几种进货方案?哪种进货方案能使商店销售完这批家电后获得的利润最大?并求出最大利润。
(利润=售价-进价)
C
B
A
D
/km
/km
2 4 6 8 10 12
8
6
4
2
第22题
22、(8分)去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水。经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图)。两村的坐标分别为A(2,3),B(12,7)。
(1)、若从节约经费考虑,水泵站建在距离大桥O多远的
地方可使所用输水管道最短?
(2)、水泵站建在距离大桥O多远的地方,可使它到张村、李村的
距离相等?
M
A
y
N
B
D
P
x
C
第23题
O
C
23、(10分)如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3。
(1) 设点P的纵坐标为p,写出p随变化的函数关系式。
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP。请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于的k值?若存在,请求出符合的k值;若不存在,请说明理由。
济宁市2011年高中阶段学校招生考试
数学试题参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
D
C
A
B
C
B
A
D
二、填空题:
11、m>1 12、y=(x-2)2+1 13、相交 14、 100 15、
三、解答题:
16、解:原式=…………………2分
= …………………4分
= …………………5分
17、证明:∵四边形ABCD是平行四边形
∴AD∥BC,OB=OD …………………1分
∵∠EDO=∠FBO, ∠OED=∠OFB …………………2分
∴△OED≌△OFB
∴DE=BF …………………3分
又∵ED∥BF
∴四边形BEDF是平行四边形 …………………4分
∵EF⊥BD
∴平行四边形BEDF是菱形。 …………………5分
18、解:过点P作PC⊥AB,垂足为C,设PC=x海里
在Rt△APC中,∵tan∠A= ∴AC= = ……………2分
67.5°
36.9°
A
C
P
B
第18题
在Rt△PCB中,∵tan∠B= ∴BC= = ……………4分
∵ AC+BC=AB=21×5 ∴+=21×5 ,解得 x=60
∵sin∠B= ∴PB= = 50× =100(海里)
∴海检船所在B处与城市P的距离为100海里。 …………6分
甲
乙
丙
竞选人
100
95
90
85
80
75
70
分数
笔试
面试
图二
19、解:(1)…2分
(2)甲的票数是:200×34%=68(票)
乙的票数是:200×30%=60(票)
丙的票数是:200×28%=56(票) …………4分
(3)甲的平均成绩:
乙的平均成绩:
丙的平均成绩:
∵乙的平均成绩最高 ∴应该录取乙。 …………6分
A
第20题
N
C
B
D
E
F
M
O
O
20、解:(1)证明:连接OE
∵AM、DE是⊙O的切线,OA、OE是⊙O的半径
∴∠ADO=∠EDO,∠DAO=∠DEO=90°…………1分
∴∠AOD=∠EOD=∠AOE …………2分
∵∠ABE=∠AOE ∴∠AOD=∠ABE ∴OD∥BE …………3分
(2) OF =CD …………4分
理由:连接OC
∵BE、CE是⊙O的切线
∴∠OCB=∠OCE …………5分
∵AM∥BN
∴∠ADO+∠EDO+∠OCB+∠OCE=180°
由(1)得 ∠ADO=∠EDO
∴2∠EDO+2∠OCE=180° 即∠EDO+∠OCE=90° …………6分
在Rt△DOC中, ∵ F是DC的中点 ∴OF =CD …………7分
21、解:(1)设商店购买彩电x台,则购买洗衣机(100-x)台。
由题意,得 2000x+1000(100-x)=160000 解得x=60
则100-x=40(台)
所以,商店可以购买彩电60台,洗衣机40台。 …………3分
(2)、设购买彩电a台,则购买洗衣机为(100-2a)台。
根据题意,得 2000a+1600a+1000(100-2a)≤160000
100-2a≤a
解得 。因为a是整数,所以 a=34、35、36、37。
因此,共有四种进货方案。 …………6分
设商店销售完毕后获得的利润为w元
则w=(2200-2000)a+(1800-1600)a+(1100-1000)(100-2a)
=200a+10000 …………7分
∵ 200>0 ∴ w随a的增大而增大
∴ 当a=37时 w最大值=200×37+10000=17400 …………8分
所以,商店获得的最大利润为17400元。
22、F
G
E
C
B
A
D
/km
/km
2 4 6 8 10 12
8
6
4
2
第22题
解:(1)作点B关于x轴的对成点E,连接AE,则点E为(12,-7)
设直线AE的函数关系式为y=kx+b,则
2k+b=3
12k+b=-7
解得 k=-1
b=5
当y=0时, x=5
所以,水泵站建在距离大桥5千米的地方,可使所用输水管道最短。
(2)作线段AB的垂直平分线GF,交AB于点F,交x轴欲点G
设点G的坐标为(x,0)
在Rt△AGD中,AG2=AD2+DG2=32+(x-2)2
在Rt△BCG中,BG2=BC2+GC2=72+(12-x)2
∵AG=BG ∴32+(x-2)2=72+(12-x)2 解得 x=9
所以 ,水泵站建在距离大桥9千米的地方,可使它到张村、李村的距离相等。
23、解:(1)、
M
A
y
N
B
D
P
x
C
第23题
O
C
∵y轴和直线l都是⊙C的切线
∴OA⊥AD BD⊥AD
又∵ OA⊥OB
∴∠AOB=∠OAD=∠ADB=90°
∴四边形OADB是矩形
∵⊙C的半径为2
∴AD=OB=4
∵点P在直线l上
∴点P的坐标为(4,p)
又∵点P也在直线AP上
∴p=4k+3
(2)连接DN
∵AD是⊙C的直径 ∴ ∠AND=90°
∵ ∠AND=90°-∠DAN,∠ABD=90°-∠DAN
∴∠AND=∠ABD
又∵∠ADN=∠AMN ∴∠ABD=∠AMN …………4分
∵∠MAN=∠BAP …………5分
∴△AMN∽△ABP …………6分
(3)存在。 …………7分
理由:把x=0代入y=kx+3得y=3,即OA=BD=3
AB=
∵ S△ABD= AB·DN=AD·DB
∴DN==
∴AN2=AD2-DN2=
∵△AMN∽△ABP
∴ 即 ……8分
当点P在B点上方时,
∵AP2=AD2+PD2 = AD2+(PB-BD)2 =42+(4k+3-3)2 =16(k2+1)
或AP2=AD2+PD2 = AD2+(BD-PB)2 =42+(3-4k-3)2 =16(k2+1)
S△ABP= PB·AD=(4k+3)×4=2(4k+3)
∴
整理得k2-4k-2=0 解得k1 =2+ k2=2- …………9分
当点P在B 点下方时,
∵AP2=AD2+PD2 =42+(3-4k-3)2 =16(k2+1)
S△ABP= PB·AD=[-(4k+3)]×4=-2(4k+3)
∴
化简,得k2+1=-(4k+3) 解得k=-2
综合以上所得,当k=2±或k=-2时,△AMN的面积等于 …10分