- 2021-05-10 发布 |
- 37.5 KB |
- 4页
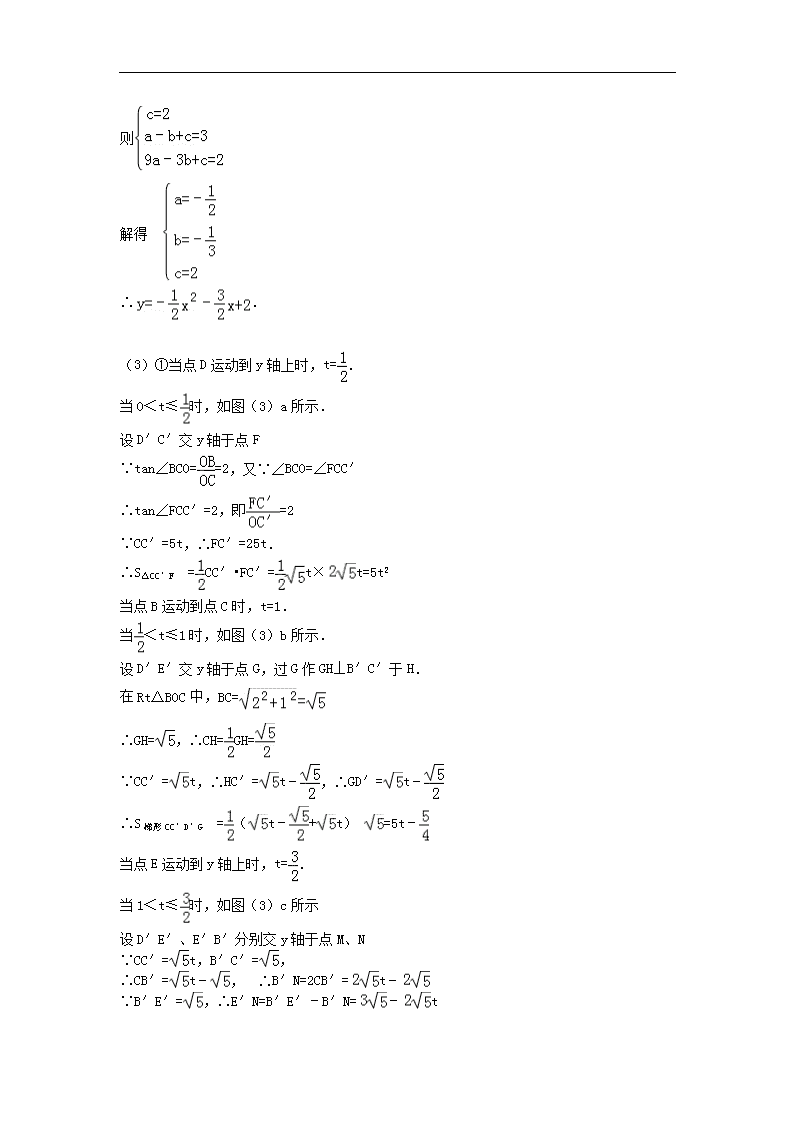

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013中考数学压轴题动态几何题型精选解析(三)
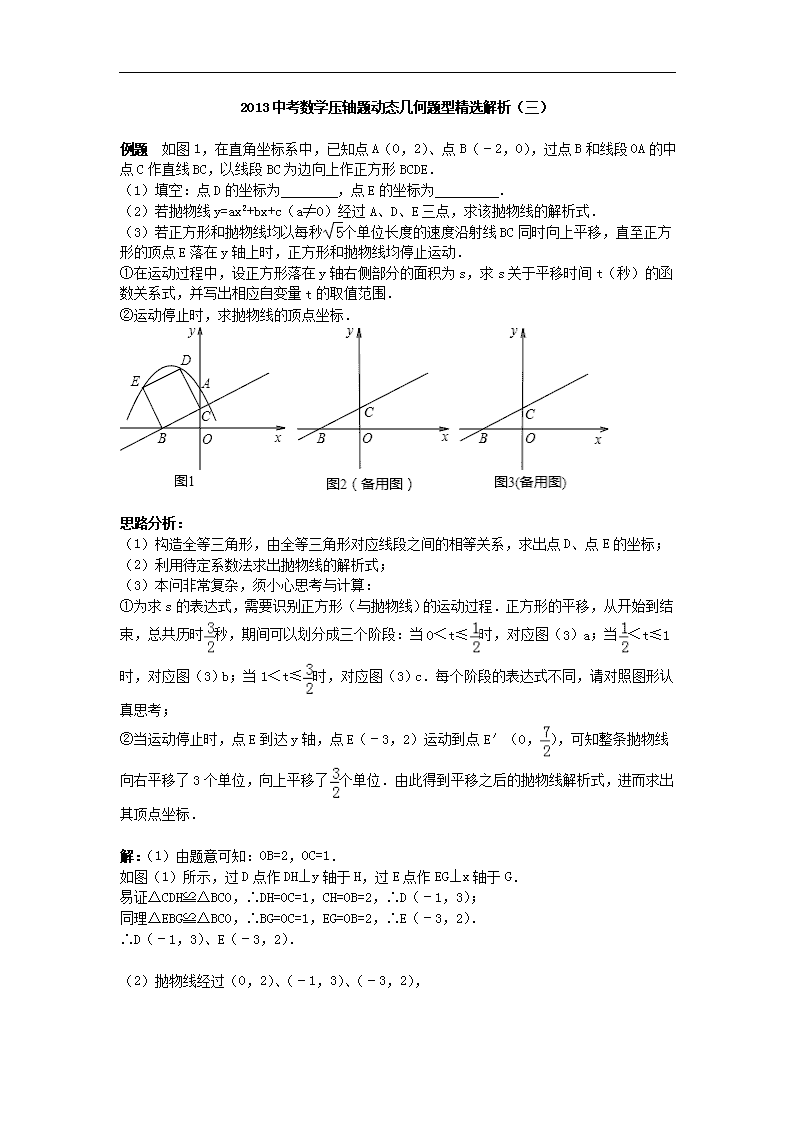
2013中考数学压轴题动态几何题型精选解析(三) 例题 如图1,在直角坐标系中,已知点A(0,2)、点B(﹣2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE. (1)填空:点D的坐标为 ,点E的坐标为 . (2)若抛物线y=ax2+bx+c(a≠0)经过A、D、E三点,求该抛物线的解析式. (3)若正方形和抛物线均以每秒个单位长度的速度沿射线BC同时向上平移,直至正方形的顶点E落在y轴上时,正方形和抛物线均停止运动. ①在运动过程中,设正方形落在y轴右侧部分的面积为s,求s关于平移时间t(秒)的函数关系式,并写出相应自变量t的取值范围. ②运动停止时,求抛物线的顶点坐标. 思路分析: (1)构造全等三角形,由全等三角形对应线段之间的相等关系,求出点D、点E的坐标; (2)利用待定系数法求出抛物线的解析式; (3)本问非常复杂,须小心思考与计算: ①为求s的表达式,需要识别正方形(与抛物线)的运动过程.正方形的平移,从开始到结束,总共历时秒,期间可以划分成三个阶段:当0<t≤时,对应图(3)a;当<t≤1时,对应图(3)b;当1<t≤时,对应图(3)c.每个阶段的表达式不同,请对照图形认真思考; ②当运动停止时,点E到达y轴,点E(﹣3,2)运动到点E′(0,),可知整条抛物线向右平移了3个单位,向上平移了个单位.由此得到平移之后的抛物线解析式,进而求出其顶点坐标. 解:(1)由题意可知:OB=2,OC=1. 如图(1)所示,过D点作DH⊥y轴于H,过E点作EG⊥x轴于G. 易证△CDH≌△BCO,∴DH=OC=1,CH=OB=2,∴D(﹣1,3); 同理△EBG≌△BCO,∴BG=OC=1,EG=OB=2,∴E(﹣3,2). ∴D(﹣1,3)、E(﹣3,2). (2)抛物线经过(0,2)、(﹣1,3)、(﹣3,2), 则 解得 ∴. (3)①当点D运动到y轴上时,t=. 当0<t≤时,如图(3)a所示. 设D′C′交y轴于点F ∵tan∠BCO==2,又∵∠BCO=∠FCC′ ∴tan∠FCC′=2,即=2 ∵CC′=5t,∴FC′=25t. ∴S△CC′F=CC′•FC′=t×t=5t2 当点B运动到点C时,t=1. 当<t≤1时,如图(3)b所示. 设D′E′交y轴于点G,过G作GH⊥B′C′于H. 在Rt△BOC中,BC= ∴GH=,∴CH=GH= ∵CC′=t,∴HC′=t﹣,∴GD′=t﹣ ∴S梯形CC′D′G=(t﹣+t) =5t﹣ 当点E运动到y轴上时,t=. 当1<t≤时,如图(3)c所示 设D′E′、E′B′分别交y轴于点M、N ∵CC′=t,B′C′=, ∴CB′=t﹣,∴B′N=2CB′=t﹣ ∵B′E′=,∴E′N=B′E′﹣B′N=﹣t ∴E′M=E′N=(﹣t) ∴S△MNE′=(﹣t)•(﹣t)=5t2﹣15t+ ∴S五边形B′C′D′MN=S正方形B′C′D′E′﹣S△MNE′=(5t2﹣15t+)=﹣5t2+15t﹣ 综上所述,S与x的函数关系式为: 当0<t≤时,S=5t2 当<t≤1时,S=5t 当1<t≤时,S=﹣5t2+15t ②当点E运动到点E′时,运动停止.如图(3)d所示 ∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′ ∴△BOC∽△E′B′C ∴ ∵OB=2,B′E′=BC= ∴ ∴CE′= ∴OE′=OC+CE′=1+= ∴E′(0,) 由点E(﹣3,2)运动到点E′(0,),可知整条抛物线向右平移了3个单位,向上平移了个单位. ∵= ∴原抛物线顶点坐标为(,) ∴运动停止时,抛物线的顶点坐标为(,). 点评: 本题是非常典型的动面型综合题,全面考查了初中数学代数几何的多个重要知识点,包括:二次函数的图象与性质、待定系数法求解析式、抛物线与几何变换(平移)、相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质等.难点在于第(3)问,识别正方形和抛物线平移过程的不同阶段是关键所在.作为中考压轴题,本题涉及考点众多,计算复杂,因而难度很大,对考生综合能力要求很高,具有很好的区分度.查看更多