中考数学旋转与相似的典型类型总结

中考数学旋转与相似的典型类型总结

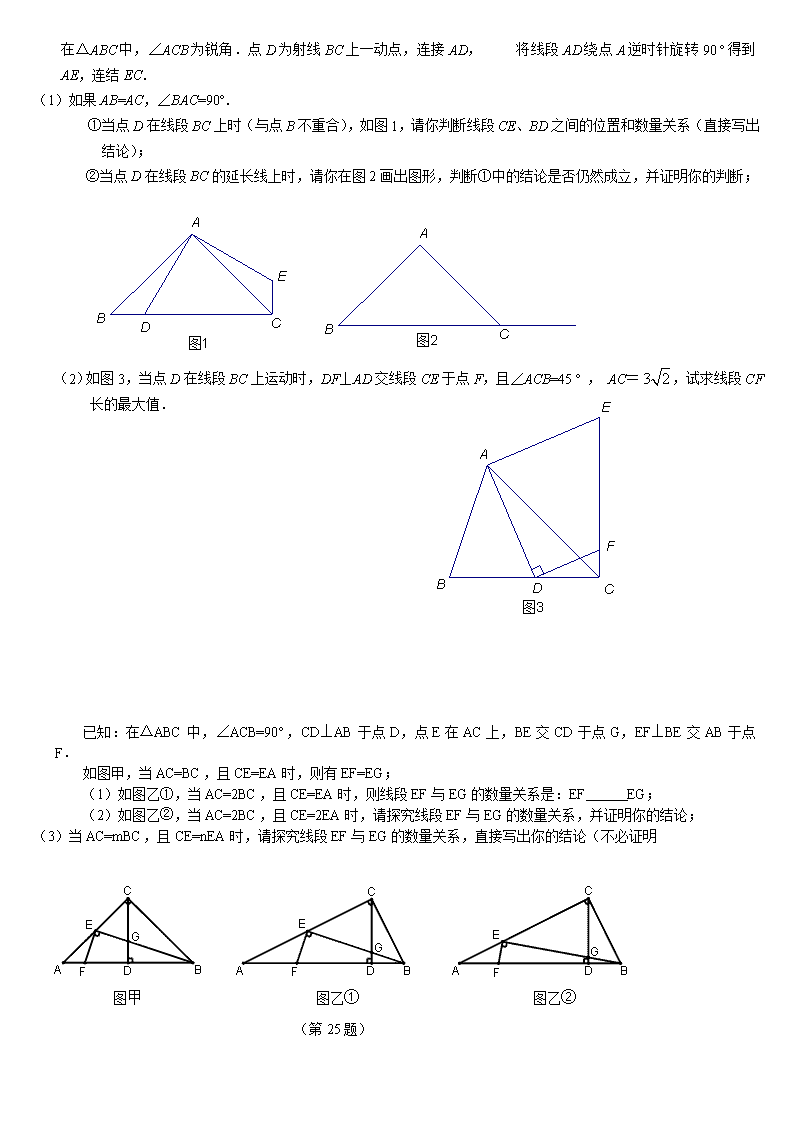
旋转与全等、相似的典型类型总结 ‎25. 含30°角的直角三角板ABC中，∠A=30°.将其绕直角顶点C顺时针旋转角（且≠ 90°），得到Rt△，边与AB所在直线交于点D，过点 D作DE∥交边于点E，连接BE.‎ ‎ （1）如图1，当边经过点B时，= °；‎ ‎ （2）在三角板旋转的过程中，若∠CBD的度数是∠CBE度数的m倍，猜想m的值并证明你的结论；‎ ‎（3） 设 BC=1，AD=x，△BDE的面积为S，以点E为圆心，EB为半径作⊙E，当S=‎ ‎ 时，求AD的长，并判断此时直线与⊙E的位置关系. ‎ ‎ ‎ 如图，在△ABC中，∠A=90°，AB=8，AC=6，M是AB上的动点（不与A、B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O中作内接矩形AMPN．令AM=x．‎ ‎（1）用含x的代数式表示△MNP的面积S；‎ ‎（2）当x为何值时，⊙O与直线BC相切？‎ ‎（3）在点M的运动过程中，设△MNP与梯形BCNM重合的面积为y，求y关于x的函数关系式，并求x为何值时，y的值最大，最大值是多少？‎ ‎（第24题）‎ ‎（第24题）‎ ‎．‎ 已知：在四边形ABCD中，AD∥BC，∠BAC＝∠D，点E、F分别在BC、CD上，且∠AEF＝∠ACD，试探究AE与EF之间的数量关系．‎ ‎(1)如图①，若AB＝BC＝AC，则AE与EF之间的数量关系为________．‎ ‎(2)如图②，若AB＝BC，你在(1)中得到的结论是否发生变化?写出你的猜想，并加以证明．‎ ‎(3)如图③，若AB＝kBC，你在(1)中得到的结论是否发生变化?写出你的猜想，并加以证明．‎ 第25题图 在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD， 将线段AD绕点A逆时针旋转90 º得到AE，连结EC．‎ ‎（1）如果AB=AC，∠BAC=90º．‎ ①当点D在线段BC上时（与点B不重合），如图1，请你判断线段CE、BD之间的位置和数量关系（直接写出结论）；‎ ②当点D在线段BC的延长线上时，请你在图2画出图形，判断①中的结论是否仍然成立，并证明你的判断；‎ ‎ ‎ ‎（2）如图3，当点D在线段BC上运动时，DF⊥AD交线段CE于点F，且∠ACB=45 º ， AC＝，试求线段CF长的最大值．‎ ‎ ‎ 已知：在△ABC中，∠ACB=90°，CD⊥AB于点D，点E在AC上，BE交CD于点G，EF⊥BE交AB于点F．‎ 如图甲，当AC=BC，且CE=EA时，则有EF=EG；‎ ‎（1）如图乙①，当AC=2BC，且CE=EA时，则线段EF与EG的数量关系是：EF EG；‎ ‎（2）如图乙②，当AC=2BC，且CE=2EA时，请探究线段EF与EG的数量关系，并证明你的结论；‎ 图乙②‎ 图乙①‎ 图甲 ‎（第25题）‎ ‎（3）当AC=mBC，且CE=nEA时，请探究线段EF与EG的数量关系，直接写出你的结论（不必证明 已知正方形ABCD，边长为3，对角线AC，BD交点O,直角MPN绕顶点P旋转，角的两边分别与线段AB,AD交于点M，N（不与点B，A，D重合）． 设DN=x，四边形AMPN的面积为y．在下面情况下，y随x的变化而变化吗？若不变，请求出面积y的值；若变化，请求出y与x的关系式．‎ ‎（1）如图1，点P与点O重合；‎ ‎（2）如图2，点P在正方形的对角线AC上，且AP=2PC；‎ ‎（3）如图3，点P在正方形的对角线BD上，且DP=2PB．‎ ‎25．在Rt△ABC中，∠ACB=90°，tan∠BAC=. 点D在边AC上（不与A，C重合），连结BD，F为BD中点.‎ ‎（1）若过点D作DE⊥AB于E，连结CF、EF、CE，如图1． 设，则k = ；‎ ‎（2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示．‎ 求证：BE-DE=2CF；‎ ‎（3）若BC=6，点D在边AC的三等分点处，将线段AD绕点A旋转，点F始终为BD中点，求线段CF长度的最大值．‎ 东城 ‎24. 等边△ABC边长为6，P为BC边上一点，∠MPN=60°，且PM、PN分别于边AB、AC交于点E、F.‎ ‎（1）如图1，当点P为BC的三等分点，且PE⊥AB时，判断△EPF的形状；‎ ‎（2）如图2，若点P在BC边上运动，且保持PE⊥AB，设BP=x，四边形AEPF面积的y，求y与x的函数关系式，并写出自变量x的取值范围；‎ ‎（3）如图3，若点P在BC边上运动，且∠MPN绕点P旋转，当CF=AE=2时，求PE的长.‎ 图1 图2 图3‎ 已知：如图，正方形中，为对角线，将绕顶点逆时针旋转°（），旋转后角的两边分别交于点、点，交于点、点，联结．‎ ‎（1）在的旋转过程中，的大小是否改变，若不变写出它的度数，若改变，写出它的变化范围（直接在答题卡上写出结果，不必证明）；‎ ‎（2）探究△与△的面积的数量关系，写出结论并加以证明．‎ ‎24． 解：（1）不变； ……………………………………………………………………1分 ‎45°；………………………………………………………………………2分 ‎（2）结论：S△AEF=2 S△APQ………………………………………………………………3分 证明：‎ ‎∵45°， ‎ ‎∴ …………………… ‎ ‎∴ …………………… ………4分 同理 …………………… ………5分 过点作于…………… ………6分 ‎∴△AEF ‎ ‎△APQ …………………………………7分 ‎22. 如图，在中，，，矩形CDEF的顶点C、D、E、F分别在边AO、OB、AB上。‎ ‎（1）若C、D恰好是边AO，OB的中点，求矩形CDEF的面积；‎ ‎（2）若，求矩形CDEF面积的最大值。‎ ‎24. 如图1，在△ABC中，AB＝BC＝5，AC=6. △ECD是△ABC沿CB方向平移得到的，连结AE，AC和BE相交于点O.‎ ‎（1）判断四边形ABCE是怎样的四边形，并证明你的结论； ‎ ‎（2）如图2，P是线段BC上一动点（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.‎ ①四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积；‎ ②当线段BP的长为何值时，以点P、Q、R为顶点的三角形与△BOC相似？‎ ‎23． 如图，在△ABC中，BC=3，AC=2，P为BC边上一个动点，过点P作PD∥AB，交AC于点D，连结BD．‎ ‎（1）如图1，若∠C=45°，请直接写出：当= 时，‎ ‎△BDP的面积最大；‎ ‎（2）如图2，若∠C=α为任意锐角，则当点P在BC上何处时，‎ ‎△BDP的面积最大？‎ ‎ ‎ ‎ ‎ ‎24．现场学习：我们知道，若锐角α的三角函数值为sinα = m，则可通过计算器得到角α的大小，这时我们用arc sin m来表示α，记作：α=arc sin m；若cos α = m，则记α = arc cos m；若tan α = m，则记α = arc tan m．‎ ‎ 解决问题：如图，已知正方形ABCD，点E是边AB上一动点，点F在AB边或其延长线上，点G在边AD上．连结ED，FG，交点为H．‎ ‎（1）如图1，若AE=BF=GD，请直接写出∠EHF= °；‎ ‎（2）如图2，若EF =CD，GD=AE，设∠EHF=α．请判断当点E在AB上运动时， ∠EHF的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请求出α． ‎ ‎24．已知在△ABC和△DBE中，AB＝AC，DB＝DE，且∠BAC＝∠BDE．‎ ‎（1）如图1，若∠BAC＝∠BDE＝60°，则线段CE与AD之间的数量关系是 ；‎ ‎（2）如图2，若∠BAC＝∠BDE＝120°，且点D在线段AB上，则线段CE与AD之 间的数量关系是__________________；‎ ‎（3）如图3，若∠BAC＝∠BDE＝，请你探究线段CE与AD之间的数量关系（用含的式子表示），并证明你的结论．‎ ‎ ‎ ‎.已知：中，，中，,. 连接、，点、、分别为、、的中点.‎ ‎ ‎ 图1 图2‎ ‎(1) 如图1，若、、三点在同一直线上，且，则的形状是________________，此时________；‎ ‎(2) 如图2，若、、三点在同一直线上，且，证明，并计算的值（用含的式子表示）；‎ ‎(3) 在图2中，固定，将绕点旋转，直接写出的最大值.‎ ‎．如图1，在□ABCD中，AE⊥BC于E，E恰为BC的中点，.‎ ‎（1）求证：AD=AE； ‎ ‎（2）如图2，点P在BE上，作EF⊥DP于点F，连结AF. ‎ 求证：；‎ ‎（3）请你在图3中画图探究：当P为射线EC上任意一点（P不与点E重合）时，作EF⊥DP于点F，连结AF，线段DF、EF与AF之间有怎样的数量关系？直接写出你的结论.‎ 图1‎ E B C A D 图3‎ E B C A D 图2‎ E C B A D F P ‎ 如图10-1‎ ‎，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合)，以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系： ‎ ‎（1）①请直接写出图10-1中线段BG、线段DE的数量关系及所在直线的位置关系；‎ ‎②将图10-1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度，得到如图10-2、如图10-3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图10-2证明你的判断．‎ ‎（2）将原题中正方形改为矩形（如图10-4～10-6），且 ，试判断（1）①中得到的结论哪个成立，哪个不成立？并写出你的判断，不必证明.‎ ‎（3）在图10-5中，连结、，且，则= ．‎ ‎(1)已知：如图1，△中，分别以、为一边向△ 外作正方形和，直线于，若于，于. 判断线段的数量关系，并证明；‎ ‎(2)如图2，梯形中，∥, 分别以两腰、为一边向梯形 外作正方形和，线段的垂直平分线交线段于点，交于点，若于，于．(1)中结论还成立吗？请说明理由.‎ 已知：如图，在中，，，，点由出发沿方向向点A匀速运动，速度为1cm/s；点Q由出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为（），解答下列问题：‎ ‎（1）当为何值时，？‎ ‎（2）设的面积为（），求与 之间的函数关系式；‎ ‎（3）是否存在某一时刻，使线段PQ恰好把 的周长和面积同时平分？若存在，求出 此时的值；若不存在，说明理由；‎