- 2021-05-10 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年中考数学专题复习模拟演练 全等三角形
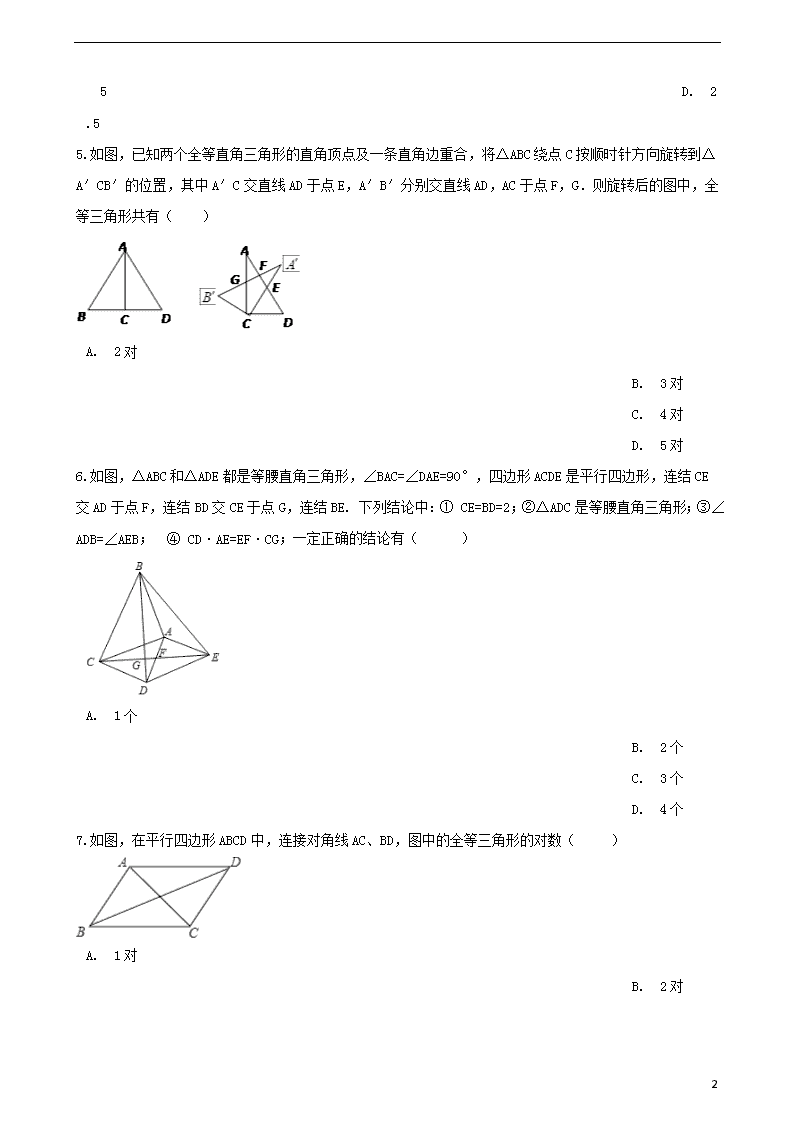
全等三角形 一、选择题 1.如图,某同学将一块三角形玻璃打碎成三块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) A. 带(1)去 B. 带(2)去 C. 带(3)去 D. 带(1)(2)去 2.已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为( ) A. 80° B. 70° C. 30° D. 100° 3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若AC=6 cm,则AE+DE等于( ) A. 4 cm B. 5 cm C. 6 cm D. 7 cm 4.如图,若△ABE≌△ACF , 且AB=5,AE=3,则EC的长为( ) A. 2 B. 3 12 C. 5 D. 2.5 5.如图,已知两个全等直角三角形的直角顶点及一条直角边重合,将△ABC绕点C按顺时针方向旋转到△A′CB′的位置,其中A′C交直线AD于点E,A′B′分别交直线AD,AC于点F,G.则旋转后的图中,全等三角形共有( ) A. 2对 B. 3对 C. 4对 D. 5对 6.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交CE于点G,连结BE. 下列结论中:① CE=BD=2;②△ADC是等腰直角三角形;③∠ADB=∠AEB; ④ CD·AE=EF·CG;一定正确的结论有( ) A. 1个 B. 2个 C. 3个 D. 4个 7.如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( ) A. 1对 B. 2对 12 C. 3对 D. 4对 8.如图已知△ABE≌△ACD, AB=AC, BE=CD,∠B=40°,∠AEC=120°则∠DAC的度数为 ( ) A. 80° B. 70° C. 60° D. 50° 9.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( ) A. 40° B. 35° C. 30° D. 25° 10.如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( ) A. B. C. D. 二、填空题 11.用直尺和圆规作一个角等于已知角得到两个角相等的依据是________ 12.如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论: ①四边形CFHE是菱形; ②EC平分∠DCH; 12 ③线段BF的取值范围为3≤BF≤4; ④当点H与点A重合时,EF=2 . 以上结论中,你认为正确的有________.(填序号) 13.如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计)________ . 14.如图,E为正方形ABCD中CD边上一点,∠DAE=30°,P为AE的中点,过点P作直线分别与AD、BC相交于点M、N.若MN=AE,则∠AMN等于________ 15.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,得到如下结论:①AC⊥BD;②AO=CO= AC;③△ABD≌△CBD,其中正确的结论有________(填序号). 16.如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动________秒时,△DEB与△BCA全等. 12 17.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图7,则∠EAB是多少度?请你说出∠EAB= ________度 18.如图(1)所示,已知AB=AC,D为∠BAC的角平分线上面的一点,连接BD、CD;如图(2)已知AB=AC,D、E、F为∠BAC的角平分线上面的三点,连接BD、CD、BE、CE、BF、CF;…,依次规律,第N个图形中有全等三角形的对数是________. 三、解答题 19.已知,如图:AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC. 20.如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0.5m/s,求这个人走了多长时间? 12 21.如图1,等边△ABC中,D是AB上一点,以CD为边向上作等边△CDE,连结AE. (1)求证:AE∥BC; (2)如图2,若点D在AB的延长线上,其余条件均不变,(1)中结论是否成立?请说明理由. 22.如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于E,DF⊥AC于F. 12 (1)证明:BE=CF; (2)如果AB=16,AC=10,求AE的长. 23.将一块正方形和一块等腰直角三角形如图1摆放. (1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM=________; (2)将△BEF绕点B旋转. ①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式:________;(不用证明) ②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由. 12 24.已知矩形纸片ABCD中,AB=2,BC=3. 操作:将矩形纸片沿EF折叠,使点B落在边CD上. 探究: (1)如图1,若点B与点D重合,你认为△EDA1和△FDC全等吗?如果全等,请给出证明,如果不全等,请说明理由; (2)如图2,若点B与CD的中点重合,请你判断△FCB1、△B1DG和△EA1G之间的关系,如果全等,只需写出结果,如果相似,请写出结果和相应的相似比; (3)如图2,请你探索,当点B落在CD边上何处,即B1C的长度为多少时,△FCB1与△B1DG全等. 12 参考答案 一、选择题 C A C B C C D A B C 二、填空题 11. SSS 12. ①③④ 13. 21 14. 60°或120° 15. ①②③ 16. 0,2,6,8 17. 35 18. n(n+1) 三、解答题 19. 证明:∵AE⊥AB,BC⊥AB, ∴∠EAD=∠CBA=90°, 在Rt△ADE和中Rt△ABC中, , ∴Rt△ADE≌Rt△ABC(HL), ∴∠EDA=∠C, 又∵在Rt△ABC中,∠B=90°, ∴∠CAB+∠C=90° ∴∠CAB+∠EDA=90°, ∴∠AFD=90°, ∴ED⊥AC 20. 解:∵∠CMD=90°, ∴∠CMA+∠DMB=90°, 又∵∠CAM=90°, ∴∠CMA+∠ACM=90°, 12 ∴∠ACM=∠DMB, 在△ACM和△BMD中, , ∴△ACM≌△BMD(AAS), ∴AC=BM=3m, ∴他到达点M时,运动时间为3÷0.5=6(s), 答:这个人从B点到M点运动了6s. 21. (1)证明:∵∠BCA=∠DCE=60°, ∴∠BCA﹣∠ACD=∠DCE﹣∠ACD, 即∠BCD=∠ACE, ∵△ABC和△DCE是等边三角形, ∴BC=AC,DC=EC, 在△BDC与△ACE中, , ∴△DBC≌△ACE(SAS), ∴∠B=∠CAE, ∴∠B=∠CAE=∠BAC=60°, ∴∠CAE+∠BAC=∠BAE=120°, ∴∠B+∠BAE=180, ∴AE∥BC (2)成立,证明如下: ∵△DBC≌△ACE, ∴∠BDC=∠AEC, 在△DMC和△AME中, ∵∠BDC=∠AEC(已证), ∴∠DMC=∠EMA, ∴△DMC∽△EMA, ∴∠EAM=∠DCM=60°, ∴∠EAC=120°, 12 又∵∠DCA+∠CAE=∠DCE+∠ECA+CEA=180°+∠ECA, ∴AE∥BC 22. (1)证明:如图,连接BD、CD. ∵DG⊥BC,BG=GC, ∴DB=DC, ∵DA平分∠BAC,DE⊥AB,DF⊥AC, ∴DE=DF, 在Rt△DEB和Rt△DFC中, , ∴△DEB≌△DFC, ∴BE=CF. (2)解:在Rt△ADE和rT△ADF中, , ∴△ADE≌△ADF, ∴AE=AF, ∴AB﹣BE=AC+CF, ∴2AE=AB﹣AC=16﹣10, ∴AE=3 23. (1)45° (2)MN=AM+CN 24. (1)解:全等. ∵四边形ABCD是矩形, 所以∠A=∠B=∠C=∠ADC=90°,AB=CD, 由题意知:∠A=∠A1 , ∠B=∠A1DF=90°,CD=A1D, 所以∠A1=∠C=90°,∠CDF+∠EDF=90°, 12 所以∠A1DE=∠CDF,所以△EDA1≌△FDC(ASA) (2)解:△B1DG和△EA1G全等. △FCB1与△B1DG相似,设FC= ,则B1F=BF= ,B1C= DC=1, 所以 ,所以 , 所以△FCB1与△B1DG相似,相似比为4:3 (3)解:△FCB1与△B1DG全等.设 ,则有 , , 在直角 中,可得 , 整理得 ,解得 (另一解舍去), 所以,当B1C= 时,△FCB1与△B1DG全等. 12查看更多