全国中考数学试题分类汇编—规律探索
(2013•衡阳)观察下列按顺序排列的等式:,,,,…,试猜想第n个等式(n为正整数):an= ﹣ .
考点:
规律型:数字的变化类.3718684
分析:
根据题意可知a1=1﹣,a2=﹣,a3=﹣,…故an=﹣.
解答:
解:通过分析数据可知第n个等式为:an=﹣.
故答案为:﹣.
点评:
本题考查了数字变化规律,培养学生通过观察、归纳、抽象出数列的规律的能力,要求学生首先分析题意,找到规律,并进行推导得出答案.
(2013,娄底)如图,是用火柴棒拼成的图形,则第个图形需__________根火柴棒.
(2013•益阳)下表中的数字是按一定规律填写的,表中a的值应是 21 .
1
2
3
5
8
13
a
…
2
3
5
8
13
21
34
…
考点:
规律型:数字的变化类.
分析:
根据第一行第3个数是前两个数值之和,进而得出答案.
解答:
解:根据题意可得出:a=13+5=21.
故答案为:21.
点评:
此题主要考查了数字变化规律,根据已知得出数字的变与不变是解题关键.
(2013,永州)电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,此WORD中为方便大家识别与印刷,我还是把图乙中的0都标出来吧,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 .(请填入方块上的字母)
(2007•荆州)观察下面的单项式:a,﹣2a2,4a3,﹣8a4,…根据你发现的规律,第8个式子是 ﹣128a8 .
考点:
规律型:数字的变化类.245761
专题:
规律型.
分析:
根据单项式可知n为双数时a的前面要加上负号,而a的系数为2(n﹣1),a的指数为n.
解答:
解:第八项为﹣27a8=﹣128a8.
点评:
本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
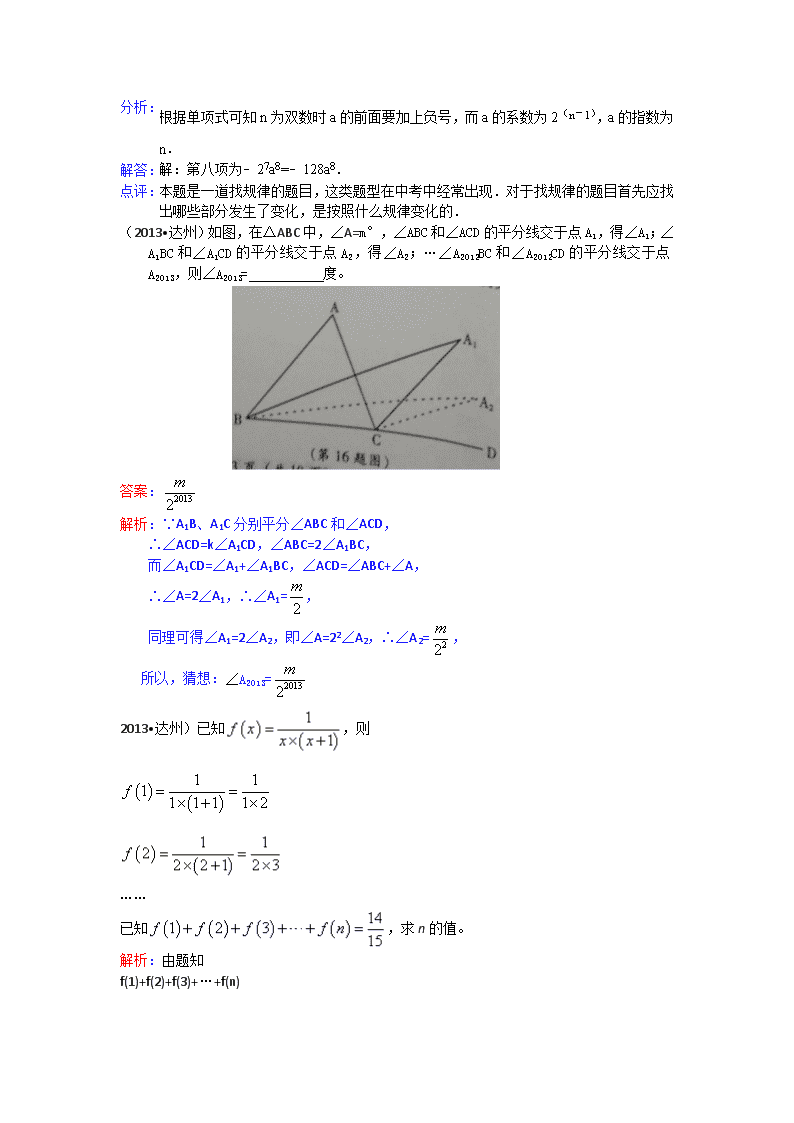
(2013•达州)如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013= 度。
答案:
解析:∵A1B、A1C分别平分∠ABC和∠ACD,
∴∠ACD=k∠A1CD,∠ABC=2∠A1BC,
而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠A1,∴∠A1=,
同理可得∠A1=2∠A2,即∠A=22∠A2,∴∠A2=,
所以,猜想:∠A2013=
2013•达州)已知,则
……
已知,求n的值。
解析:由题知
f(1)+f(2)+f(3)+…+f(n)
=+++…+
=1-+-+-+…+-
=1-………………………(4分)
=.………………………(4分)
又∵f(1)+f(2)+f(3)+…+f(n)=,
∴=.
解得n=14.………………………(6分)
经检验,n=14是上述方程的解.
故n的值为14.………………………(7分)
(2013•广安)已知直线y=x+(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2012= .
考点:
一次函数图象上点的坐标特征.3718684
专题:
规律型.
分析:
令x=0,y=0分别求出与y轴、x轴的交点,然后利用三角形面积公式列式表示出Sn,再利用拆项法整理求解即可.
解答:
解:令x=0,则y=,
令y=0,则﹣x+=0,
解得x=,
所以,Sn=••=(﹣),
所以,S1+S2+S3+…+S2012=(﹣+﹣+﹣+…+﹣)=(﹣)=.
故答案为:.
点评:
本题考查的是一次函数图象上点的坐标特点,表示出Sn,再利用拆项法写成两个数的差是解题的关键,也是本题的难点.
2013•乐山)对非负实数x “四舍五入”到个位的值记为
,即当n为非负整数时,若n-≤x =n,如<0.46>=0,<3.67>=4,给出下列关于的结论: ① <1.493>=1, ② <2x>=2, ③ 若=4,则实数x的取值范围是9≤x<11, ④ 当x≥0,m为非负整数时,有= m+<2013x>, ⑤ =+. 其中,正确的结论有 (填写所有正确的序号)。
(2013•泸州)如图,,,……在函数的图像上,,,,……都是等腰直角三角形,斜边、、,……都在轴上(n是大于或等于2的正整数),则点的坐标是 ;点的坐标是 (用含n的式子表示).
(2013•绵阳)把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现用等式AM=(i,j)表示正奇数M是第i组第j个数(从左往右数),如A7=(2,3),则A2013=( )
A.(45,77) B.(45,39) C.(32,46) D.(32,23)
(2013•遂宁)为庆祝“六•一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆第(n)图,需用火柴棒的根数为 6n+2 .
考点:
规律型:图形的变化类.
专题:
规律型.
分析:
观察不难发现,后一个图形比前一个图形多6根火柴棒,然后根据此规律写出第n个图形的火柴棒的根数即可.
解答:
解:第1个图形有8根火柴棒,
第2个图形有14根火柴棒,
第3个图形有20根火柴棒,
…,
第n个图形有6n+2根火柴棒.
故答案为:6n+2.
点评:
本题是对图形变化规律的考查,查出前三个图形的火柴棒的根数,并观察出后一个图形比前一个图形多6根火柴棒是解题的关键.
(3分)(2013•雅安)已知一组数2,4,8,16,32,…,按此规律,则第n个数是 2n .
考点:
规律型:数字的变化类.
分析:
先观察所给的数,得出第几个数正好是2的几次方,从而得出第n个数是2的n次方.
解答:
解:∵第一个数是2=21,
第二个数是4=22,
第三个数是8=23,
∴第n个数是2n;
故答案为:2n.
点评:
此题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决实际问题,本题的关键是第几个数就是2的几次方.
(2013•资阳)从所给出的四个选项中,选出适当的一个填入问号所在位置,使之呈现相同的特征 B
(2013•资阳)已知在直线上有n(n≥2的正整数)个点,每相邻两点间距离为1,从左边第1个点起跳,且同时满足以下三个条件:①每次跳跃均尽可能最大;②跳n次后必须回到第1个点;③这n次跳跃将每个点全部到达.设跳过的所有路程之和为Sn,则=______________.312
(2013•自贡)如图,在函数的图象上有点P1、P2、P3…、Pn、Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn,则S1= 4 ,Sn= .(用含n的代数式表示)
考点:
反比例函数系数k的几何意义.3718684
专题:
规律型.
分析:
求出P1、P2、P3、P4…的纵坐标,从而可计算出S1、S2、S3、S4…的高,进而求出S1、S2、S3、S4…,从而得出Sn的值.
解答:
解:当x=2时,P1的纵坐标为4,
当x=4时,P2的纵坐标为2,
当x=6时,P3的纵坐标为,
当x=8时,P4的纵坐标为1,
当x=10时,P5的纵坐标为:,
…
则S1=2×(4﹣2)=4=2[﹣];
S2=2×(2﹣)=2×=2[﹣];
S3=2×(﹣1)=2×=2[﹣];
…
Sn=2[﹣]=;
故答案为:4,.
点评:
此题考查了反比例函数图象上点的坐标特征,根据坐标求出个阴影的面积表达式是解题的关键.
(2013•沈阳)有一组等式:
请观察它们的构成规律,用你发现的规律写出第8个等式为_________
2013•恩施州)把奇数列成下表,
根据表中数的排列规律,则上起第8行,左起第6列的数是 171 .
考点:
规律型:数字的变化类.
分析:
根据第6列数字从31开始,依次加14,16,18…得出第8行数字,进而求出即可.
解答:
解:由图表可得出:第6列数字从31开始,依次加14,16,18…
则第8行,左起第6列的数为:31+14+16+18+20+22+24+26=171.
故答案为:171.
点评:
此题主要考查了数字变化规律,根据已知得出没行与每列的变化规律是解题关键.
(2013•黄石)在计数制中,通常我们使用的是“十进位制”,即“逢十进一”。而计数制方法很多,如60进位制:60秒化为1分,60分化为1小时;24进位制:24小时化为1天;7进位制:7天化为1周等…而二进位制是计算机处理数据的依据。已知二进位制与十进位制的比较如下表:
十进位制
0
1
2
3
4
5
6
…
二进制
0
1
10
11
100
101
110
…
请将二进制数10101010(二)写成十进制数为 .
答案:
解析:10101010(二)=1×27+1×25+1×23+1×2=170
(2013•荆州)如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
(2013•荆州)如图,△ABC是斜边AB的长为3的等腰直角三角形,在△ABC内作第1个内接正方形A1B1D1E1(D1、E1在AB上,A1、B1分别在AC、BC上),再在△A1B1C内接同样的方法作第2个内接正方形A2B2D2E2,…如此下去,操作n次,则第n个小正方形AnBnDnEn 的边长是
(2013•十堰)如图,是一组按照某种规律摆放成的图案,则图5中三角形的个数是( )
A.
8
B.
9
C.
16
D.
17
考点:
规律型:图形的变化类.3718684
分析:
对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,进而得出即可.
解答:
解:由图可知:第一个图案有三角形1个.第二图案有三角形1+3=5个.
第三个图案有三角形1+3+4=8个,
第四个图案有三角形1+3+4+4=12
第五个图案有三角形1+3+4+4+4=16
故选:C.
点评:
此题主要考查了图形的变化规律,注意由特殊到一般的分析方法.这类题型在中考中经常出现.
(2013•武汉)两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,……,那么六条直线最多有( )
A.21个交点 B.18个交点 C.15个交点 D.10个交点
答案:C
解析:两条直线的最多交点数为:×1×2=1,
三条直线的最多交点数为:×2×3=3,
四条直线的最多交点数为:×3×4=6,
所以,六条直线的最多交点数为:×5×6=15,
(2013•孝感)如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是 51 .
考点:
规律型:图形的变化类.
专题:
规律型.
分析:
计算不难发现,相邻两个图形的小石子数的差值依次增加3,根据此规律依次进行计算即可得解.
解答:
解:∵5﹣1=4,
12﹣5=7,
22﹣12=10,
∴相邻两个图形的小石子数的差值依次增加3,
∴第4个五边形数是22+13=35,
第5个五边形数是35+16=51.
故答案为:51.
点评:
本题是对图形变化规律的考查,仔细观察图形求出相邻两个图形的小石子数的差值依次增加3是解题的关键.
(2013•张家界)如图,OP=1,过P作且,得;再过作且=1,得;又过作且,得2;…依此法继续作下去,得 .
(2013•张家界)阅读材料:求值:
解:设 ,将等式两边同时乘以2得:
将下式减去上式得
即
请你仿照此法计算:(1)
(2) (其中n为正整数)
解:(1)设 …………………………1分
则2 ……………………2分
∴ …………………………………3分
即 ……………………4分
(2)设 ……………………………5分
则 …………………………6分
∴ 3 …………………………………7分
即2
∴ 1+
.(2013•龙岩)对于任意非零实数a、b,定义运算“”,使下列式子成立:
,,,,…,则___________.
(2013•三明)观察下列各数,它们是按一定规律排列的,则第n个数是 .
,,,,,…
考点:
规律型:数字的变化类.
专题:
规律型.
分析:
观察不难发现,分母为2的指数次幂,分子比分母小1,根据此规律解答即可.
解答:
解:∵2=21,4=22,8=23,16=24,32=25,…
∴第n个数的分母是2n,
又∵分子都比相应的分母小1,
∴第n个数的分子为2n﹣1,
∴第n个数是.
故答案为:.
点评:
本题是对数字变化规律的考查,熟练掌握2的指数次幂是解题的关键.
2013•常州)用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则S=a+b﹣1(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点中的两个多边形:
根据图中提供的信息填表:
格点多边形各边上的格点的个数
格点边多边形内部的格点个数
格点多边形的面积
多边形1
8
1
多边形2
7
3
…
…
…
…
一般格点多边形
a
b
S
则S与a、b之间的关系为S= a+2(b﹣1) (用含a、b的代数式表示).
考点:
规律型:图形的变化类.3718684
分析:
根据8=8+2(1﹣1),11=7+2(3﹣1)得到S=a+2(b﹣1).
解答:
解:填表如下:
格点多边形各边上的格点的个数
格点边多边形内部的格点个数
格点多边形的面积
多边形1
8
1
8
多边形2
7
3
11
…
…
…
…
一般格点多边形
a
b
S
则S与a、b之间的关系为S=a+2(b﹣1)(用含a、b的代数式表示).
点评:
考查了作图﹣应用与设计作图.此题需要根据图中表格和自己所算得的数据,总结出规律.寻找规律是一件比较困难的活动,需要仔细观察和大量的验算.
(2013•淮安)观察一列单项式:1x,3x2,5x2,7x,9x2,11x2,…,则第2013个单项式是 4025x2 .
考点:
单项式.3718684
专题:
规律型.
分析:
先看系数的变化规律,然后看x的指数的变化规律,从而确定第2013个单项式.
解答:
解:系数依次为1,3,5,7,9,11,…2n﹣1;
x的指数依次是1,2,2,1,2,2,1,2,2,可见三个单项式一个循环,
故可得第2013个单项式的系数为4025;
∵=671,
∴第2013个单项式指数为2,
故可得第2013个单项式是4025x2.
故答案为:4025x2.
点评:
本题考查了单项式的知识,属于规律型题目,解答本题关键是观察系数及指数的变化规律.
2013•南宁)有这样一组数据a1,a2,a3,…an,满足以下规律:,(n≥2且n为正整数),则a2013的值为 ﹣1 (结果用数字表示).
考点:
规律型:数字的变化类.3718684
专题:
规律型.
分析:
求出前几个数便不难发现,每三个数为一个循环组依次循环,用过2013除以3,根据商和余数的情况确定答案即可.
解答:
解:a1=,
a2==2,
a3==﹣1,
a4==,
…,
依此类推,每三个数为一个循环组依次循环,
∵2013÷3=671,
∴a2013为第671循环组的最后一个数,与a3相同,为﹣1.
故答案为:﹣1.
点评:
本题是对数字变化规律的考查,根据计算得到每三个数为一个循环组依次循环是解题的关键.
(2013•玉林)一列数a1,a2,a3,…,其中a1=,an=(n为不小于2的整数),则a100=( )
A.
B.
2
C.
﹣1
D.
﹣2
考点:
规律型:数字的变化类.
专题:
规律型.
分析:
根据表达式求出前几个数不难发现,每三个数为一个循环组依次循环,用100除以3,根据商和余数的情况确定a100的值即可.
解答:
解:根据题意得,a2==2,
a3==﹣1,
a4==,
a5==2,
…,
依此类推,每三个数为一个循环组依次循环,
∵100÷3=33…1,
∴a100是第34个循环组的第一个数,与a1相同,
即a100=.
故选A.
点评:
本题是对数字变化规律的考查,计算并观察出每三个数为一个循环组依次循环是解题的关键.
(2013•呼和浩特)如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.
A.
156
B.
157
C.
158
D.
159
考点:
规律型:图形的变化类.3718684
分析:
根据第1个图案需7根火柴,7=1×(1+3)+3,第2个图案需13根火柴,13=2×(2+3)+3,第3个图案需21根火柴,21=3×(3+3)+3,得出规律第n个图案需n(n+3)+3根火柴,再把11代入即可求出答案.
解答:
解:根据题意可知:
第1个图案需7根火柴,7=1×(1+3)+3,
第2个图案需13根火柴,13=2×(2+3)+3,
第3个图案需21根火柴,21=3×(3+3)+3,
…,
第n个图案需n(n+3)+3根火柴,
则第11个图案需:11×(11+3)+3=157(根);
故选B.
点评:
此题主要考查了图形的变化类,关键是根据题目中给出的图形,通过观察思考,归纳总结出规律,再利用规律解决问题,难度一般偏大,属于难题.
(2013•北京) 如图,在平面直角坐标系O中,已知直线:,双曲线。在上取点A1,过点A1作轴的垂线交双曲线于点B1,过点B1作轴的垂线交于点A2,请继续操作并探究:过点A2作轴的垂线交双曲线于点B2,过点B2作
轴的垂线交于点A3,…,这样依次得到上的点A1,A2,A3,…,An,…。记点An的横坐标为,若,则=__________,=__________;若要将上述操作无限次地进行下去,则不能取的值是__________
答案:
解析:根据求出;根据求出;
根据求出;
根据求出;
根据求出;
根据求出;
至此可以发现本题为循环规律,3次一循环,∵;[来~%#源:*&中教网]
∴;
重复上述过程,可求出、、、、、、;
由上述结果可知,分母不能为,故不能取和.
【点评】找规律的题目,规律类型有两种类型,递进规律和循环规律,对于循环规律类型,
多求几种特殊情况发现循环规律是最重要的.
(2013山东滨州,18,4分)观察下列各式的计算过程:
5×5=0×1×100+25,
15×15=1×2×100+25,
25×25=2×3×100+25,
35×35=3×4×100+25,
…… ……
请猜测,第n个算式(n为正整数)应表示为____________________________.
【答案】 [10(n-1)+5]×[10(n-1)+5]=100n(n-1)+25.
(2013• 德州)如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为( )
A.
(1,4)
B.
(5,0)
C.
(6,4)
D.
(8,3)
考点:
规律型:点的坐标.
专题:
规律型.
分析:
根据反射角与入射角的定义作出图形,可知每6次反弹为一个循环组依次循环,用2013除以6,根据商和余数的情况确定所对应的点的坐标即可.
解答:
解:如图,经过6次反弹后动点回到出发点(0,3),
∵2013÷6=335…3,
∴当点P第2013次碰到矩形的边时为第336个循环组的第3次反弹,
点P的坐标为(8,3).
故选D.
点评:
本题是对点的坐标的规律变化的考查了,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键,也是本题的难点.
(2013• 东营)如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 .
y
x
O
1
2
4
3
5
6
7
8
1
2
3
4
(2013• 济南)如图,动点P从(0,3)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2013次碰到矩形的边时,点P的坐标为
A.(1,4)
B.(5,0)
C.(6,4)
D.(8,3)
(2013山东莱芜,17,4分)已知123456789101112…997998999是由连续整数1至999排列组成的一个数,在该数种从左往右数第2013位上的数字为 .
【答案】7
(2013聊城)如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1
(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示)
考点:规律型:点的坐标.
专题:规律型.
分析:根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可.
解答:解:由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
所以,点A4n+1(2n,1).
故答案为:(2n,1).
点评:本题考查了点的坐标的变化规律,仔细观察图形,分别求出n=1、2、3时对应的点A4n+1的对应的坐标是解题的关键.
(2013• 日照)如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是
A. M=mn B. M=n(m+1) C.M=mn+1 D.M=m(n+1)
答案:D
解析:因为3=(2+1)×1,,15=(4+1)×3,35=(6+1)×5,所以,M=(n+1)×m,选D。
(2013泰安)观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…
解答下列问题:3+32+33+34…+32013的末位数字是( )
A.0 B.1 C.3 D.7
考点:尾数特征.
分析:根据数字规律得出3+32+33+34…+32013的末位数字相当于:3+7+9+1+…+3进而得出末尾数字.
解答:解:∵31=3,32=9,33=27,34=81,35=243,36=729,37=2187…
∴末尾数,每4个一循环,
∵2013÷4=503…1,
∴3+32+33+34…+32013的末位数字相当于:3+7+9+1+…+3的末尾数为3,
故选:C.
点评:此题主要考查了数字变化规律,根据已知得出数字变化规律是解题关键.
(2013•威海)如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2013的坐标为 (0,﹣2) .
考点:
中心对称;规律型:点的坐标.
专题:
规律型.
分析:
计算出前几次跳跃后,点P1,P2,P3,P4,P5,P6,P7的坐标,可得出规律,继而可求出点P2013的坐标.
解答:
解:点P1(2,0),P2(﹣2,2),P3(0,﹣2),P4(2,2),P5(﹣2,0),P6
(0,0),P7(2,0),
从而可得出6次一个循环,
∵=503…3,
∴点P2013的坐标为(0,﹣2).
故答案为:(0,﹣2).
点评:
本题考查了中心对称及点的坐标的规律变换,解答本题的关键是求出前几次跳跃后点的坐标,总结出一般规律.
.(2013• 潍坊)当白色小正方形个数等于1,2,3…时,由白色小正方形和和黑色小正方形组成的图形分别如图所示.则第个图形中白色小正方形和黑色小正方形的个数总和等于_____________.(用表示,是正整数)
(2013• 淄博)如下表,从左到右在每个小格中都填入一个整数,使得任意三个相邻格子所填整数之和都相等,则第2013个格子中的整数是 .
-4
a
b
c
6
b
-2
…
(2013•湖州)将连续正整数按以下规律排列,则位于第7行第7列的数x是 85 .
考点:
规律型:数字的变化类.
分析:
先根据第一行的第一列与第二列相差2,往后分别相差3,4,5,6,7,第二行的第一列与第二列相差3,往后分别相差4,5,6,7,第三行的第一列与第二列相差4,往后分别相差5,6,7,8,由此得出第七行的第一列与第二列分别相差8,往后分别相,9,10,11,12,13,从而求出答案.
解答:
解:第一行的第一列与第二列差个2,第二列与第三列差个3,第三列与第四列差个4,…第六列与第七列差个7,
第二行的第一列与第二列差个3,第二列与第三列差个4,第三列与第四列差个5,…第五列与第六列差个7,
第三行的第一列与第二列差个4,第二列与第三列差个5,第三列与第四列差个6,第四列与第五列差个7,
…
第七行的第一列与第二列差个8,是30,第二列与第三列差个9,是39,第三列与第四列差个10,是49,第四列与第五列差个11,是60,
第五列与第六列差个12,是72,第六列与第七列差个13,是85;
故答案为:85.
点评:
此题考查了数字的变化类,这是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题,解决本题的关键是得到每行中前一列与后一列的关系.
A
B
D
C
A1
C1
B1
D1
A2
B2
C2
D2
A3
C3
B3
D3
…
第16题
(2013• 衢州)如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形
ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形
A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边
形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继
续下去…….则四边形A2B2C2D2的周长是 ▲ ;四边
形A2013B2013C2013D2013的周长是 ▲ .
(2013• 台州)任何实数a,可用表示不超过a的最大整数,如,现对72进行如下操作:,这样对72只需进行3次操作后变为1,类似地,①对81只需进行 次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 。
(2013•深圳)观察下列等式(式子中的“!”是一种数学运算符号)
1! = 1,2! = 2×1,3! = 3×2×1,4! = 4×3×2×1,……,
那么计算:=_______。m
(2013•珠海)如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第六个正方形A6B6C6D6周长是 .
考点:
中点四边形.3481324
专题:
规律型.
分析:
根据题意,利用中位线定理可证明顺次连接正方形ABCD四边中点得正方形A1B1C1D1的面积为正方形ABCD面积的一半,根据面积关系可得周长关系,以此类推可得正方形A6B6C6D6 的周长.
解答:
解:顺次连接正方形ABCD四边的中点得正方形A1B1C1D1,则得正方形A1B1C1D1的面积为正方形ABCD面积的一半,即,则周长是原来的;
顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2,则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半,即,则周长是原来的;
顺次连接正方形A2B2C2D2得正方形A3B3C3D3,则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半,即,则周长是原来的;
顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4,则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半,则周长是原来的;
…
以此类推:第六个正方形A6B6C6D6周长是原来的,
∵正方形ABCD的边长为1,
∴周长为4,
∴第六个正方形A6B6C6D6周长是.
故答案为:.
点评:
本题考查了利用了三角形的中位线的性质,相似图形的面积比等于相似比的平方的性质.进而得到周长关系.
2013•牡丹江)如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 ()n﹣1 .
考点:
菱形的性质.3718684
专题:
规律型.
分析:
连接DB于AC相交于M,根据已知和菱形的性质可分别求得AC,AE,AG的长,从而可发现规律根据规律不难求得第n个菱形的边长.
解答:
解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=1,
∴BM=,
∴AM=,
∴AC=,
同理可得AE=AC=()2,AG=AE=3=()3,
按此规律所作的第n个菱形的边长为()n﹣1,
故答案为()n﹣1.
点评:
此题主要考查菱形的性质、等边三角形的判定和性质以及学生探索规律的能力.
(2013•绥化)如图所示,以O为端点画六条射线后OA,OB,OC,OD,OE,O后F,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2013个点在射线 OC 上.
考点:
规律型:图形的变化类.
分析:
根据规律得出每6个数为一周期.用2013除以3,根据余数来决定数2013在哪条射线上.
解答:
解:∵1在射线OA上,
2在射线OB上,
3在射线OC上,
4在射线OD上,
5在射线OE上,
6在射线OF上,
7在射线OA上,
…
每六个一循环,
2013÷6=335…3,
∴所描的第2013个点在射线和3所在射线一样,
∴所描的第2013个点在射线OC上.
故答案为:OC.
点评:
此题主要考查了数字变化规律,根据数的循环和余数来决定数的位置是解题关键.
(2013兰州)如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为 .
考点:规律型:点的坐标.
专题:规律型.
分析:根据勾股定理列式求出AB的长,再根据第四个三角形与第一个三角形的位置相同可知每三个三角形为一个循环组依次循环,然后求出一个循环组旋转前进的长度,再用2013除以3,根据商为671可知第2013个三角形的直角顶点为循环组的最后一个三角形的顶点,求出即可.
解答:解:∵点A(﹣3,0)、B(0,4),
∴AB==5,
由图可知,每三个三角形为一个循环组依次循环,一个循环组前进的长度为:4+5+3=12,
∵2013÷3=671,
∴△2013的直角顶点是第671个循环组的最后一个三角形的直角顶点,
∵671×12=8052,
∴△2013的直角顶点的坐标为(8052,0).
故答案为:(8052,0).
点评:本题是对点的坐标变化规律的考查了,难度不大,仔细观察图形,得到每三个三角形为一个循环组依次循环是解题的关键,也是求解的难点.
(2013•乌鲁木齐)如图所示的数码叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为,每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为( )
A.
B.
C.
D.
考点:
规律型:数字的变化类.3797161
分析:
根据“莱布尼兹调和三角形”的特征,每个数是它下一个行左右相邻两数的和,得出将杨晖三角形中的每一个数Cnr都换成分数得到莱布尼兹三角形,得到一个莱布尼兹三角形,从而可求出第n(n≥3)行第3个数字,进而可得第8行第3个数.
解答:
解:将杨晖三角形中的每一个数Cnr都换成分数,得到莱布尼兹三角形,
杨晖三角形中第n(n≥3)行第3个数字是Cn﹣12,
则“莱布尼兹调和三角形”第n(n≥3)行第3个数字是=,
则第8行第3个数(从左往右数)为=;
故选B.
点评:
本题考查了数字的变化类,解题的关键是通过观察、分析、归纳推理,得出各数的关系,找出规律.
(2013•江西)观察下列图形中点的个数,若按其规律再画下去,可以得到第n个图形中所有的个数为 (用含n的代数式表示).
【答案】 (n+1)2 .
【考点解剖】 本题考查学生的观察概括能力,发现规律,列代数式.
【解题思路】 找出点数的变化规律,先用具体的数字等式表示,再用含字母的式子表示.
【解答过程】 略.
【方法规律】 由图形的变化转化为数学式子的变化,加数为连续奇数,结果为加数个数的平方.
【关键词】 找规律 连续奇数的和
(2013,河北)如图12,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x 轴于点A2;
将C2绕点A2旋转180°得C3,交x 轴于点A3;
……
如此进行下去,直至得C13.若P(37,m)
在第13段抛物线C13上,则m =_________.
(2013•铜仁)如图,已知∠AOB=45°,A1、A2、A3、……在射线OA上,B1、B2、B3、……在射线OB上,且A1B1⊥OA,A2B2⊥OA,……AnBn⊥OA; A1B1⊥OB,……,An+1Bn⊥OB(n=1,2,3,4,5,6……),若OA1=1,则A6B6的长是否 .
(2013•大兴安岭)如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°………按此规律所作的第n个菱形的边长是
(2013•红河)下列图形是由一些小正方形和实心圆按一定规律排列而成的,如图所示,按此规律排列下去,第20个图形中有 42 个实心圆.
…
…
(1)
(2)
(3)
(2013•重庆B)下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为
A.51 B.70 C.76 D.81