- 2021-05-10 发布 |
- 37.5 KB |
- 18页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市黄浦区中考数学二模试卷含解析
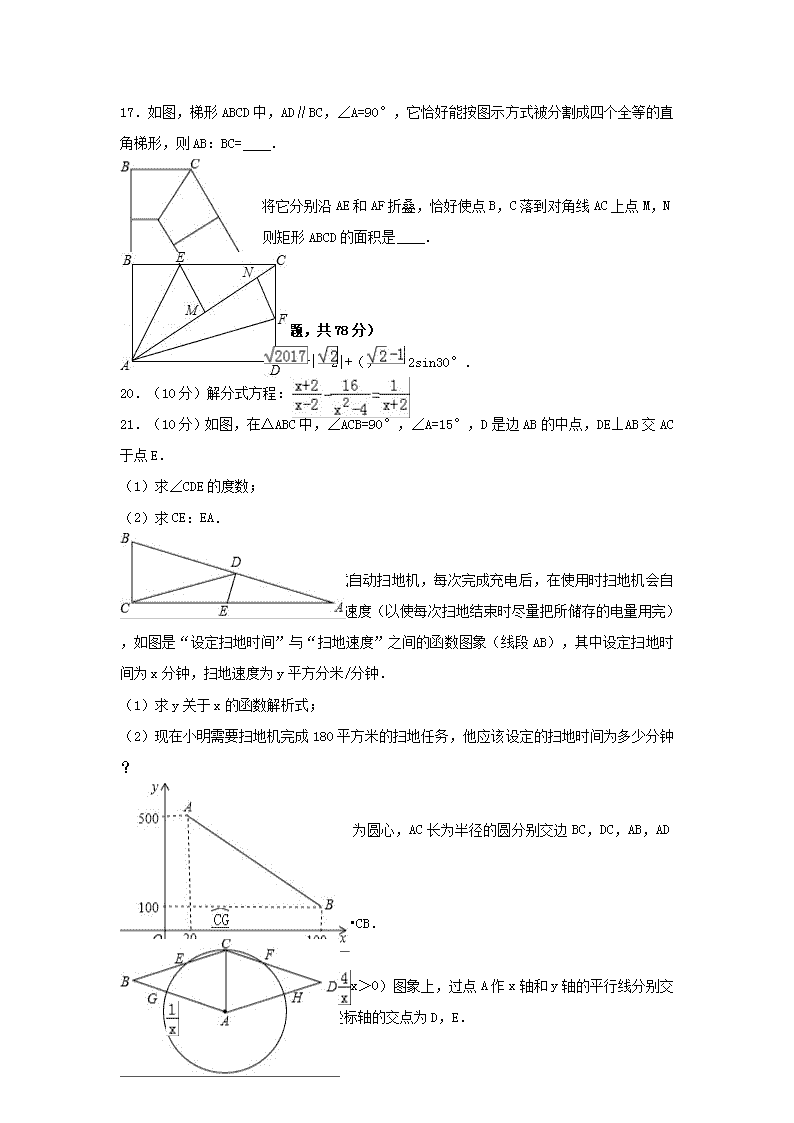
2017年上海市黄浦区中考数学二模试卷 一、选择题(本大题共6小题,每小题4分,共24分) 1.单项式4xy2z3的次数是( ) A.3 B.4 C.5 D.6 2.下列方程中,无实数解的是( ) A.2+x=0 B.2﹣x=0 C.2x=0 D. =0 3.下列各组数据中,平均数和中位数相等的是( ) A.1,2,3,4,5 B.1,3,4,5,6 C.1,2,4,5,6 D.1,2,3,5,6 4.二次函数y=﹣(x﹣2)2﹣3的图象的顶点坐标是( ) A.(2,3) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3) 5.以一个面积为1的三角形的三条中位线为三边的三角形的面积为( ) A.4 B.2 C. D. 6.已知点A(4,0),B(0,3),如果⊙A的半径为1,⊙B的半径为6,则⊙A与⊙B的位置关系是( ) A.内切 B.相交 C.外切 D.外离 二、填空题(本大题共12小题,每小题4分,共48分) 7.计算:(x2)3= . 8.因式分解:x2﹣4y2= . 9.不等式组的解集是 . 10.方程=2的解是 . 11.关于x的一元二次方程2x2﹣3x+m=0有两个相等的实数根,则实数m= . 12.某个工人要完成3000个零件的加工,如果该工人每小时能加工x个零件,那么完成这批零件的加工需要的时间是 小时. 13.已知二次函数的图象经过点(1,3)和(3,3),则此函数图象的对称轴与x轴的交点坐标是 . 14.从1到10这10个正整数中任取一个,该正整数恰好是3的倍数的概率是 . 15.正八边形一个内角的度数为 . 16.在平面直角坐标系中,点A(2,0),B(0,﹣3),若=,则点C的坐标为 . 17.如图,梯形ABCD中,AD∥BC,∠A=90°,它恰好能按图示方式被分割成四个全等的直角梯形,则AB:BC= . 18.如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是 . 三、解答题(本大题共7小题,共78分) 19.(10分)计算:(﹣1)0+|﹣2|+()﹣1﹣2sin30°. 20.(10分)解分式方程:. 21.(10分)如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E. (1)求∠CDE的度数; (2)求CE:EA. 22.(10分)小明家买了一台充电式自动扫地机,每次完成充电后,在使用时扫地机会自动根据设定扫地时间,来确定扫地的速度(以使每次扫地结束时尽量把所储存的电量用完),如图是“设定扫地时间”与“扫地速度”之间的函数图象(线段AB),其中设定扫地时间为x分钟,扫地速度为y平方分米/分钟. (1)求y关于x的函数解析式; (2)现在小明需要扫地机完成180平方米的扫地任务,他应该设定的扫地时间为多少分钟? 23.(12分)如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H. (1)求证:CE=CF; (2)当E为弧中点时,求证:BE2=CE•CB. 24.(12分)如图,点A在函数y=(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=图象于点B,C,直线BC与坐标轴的交点为D,E. (1)当点C的横坐标为1时,求点B的坐标; (2)试问:当点A在函数y=(x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由. (3)试说明:当点A在函数y=(x>0)图象上运动时,线段BD与CE的长始终相等. 25.(14分)已知:Rt△ABC斜边AB上点D,E,满足∠DCE=45°. (1)如图1,当AC=1,BC=,且点D与A重合时,求线段BE的长; (2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2; (3)如图3,当AC=3,BC=4时,设AD=x,BE=y,求y关于x的函数关系式,并写出定义域. 2017年上海市黄浦区中考数学二模试卷 参考答案与试题解析 一、选择题(本大题共6小题,每小题4分,共24分) 1.单项式4xy2z3的次数是( ) A.3 B.4 C.5 D.6 【考点】42:单项式. 【分析】单项式的次数是指各字母的指数之和 【解答】解:该单项式的次数为:1+2+3=6, 故选(D) 【点评】本题考查单项式的概念,解题的关键是正确理解单项式的次数概念,本题属于基础题型. 2.下列方程中,无实数解的是( ) A.2+x=0 B.2﹣x=0 C.2x=0 D. =0 【考点】B2:分式方程的解. 【分析】根据解方程,可得答案. 【解答】解:A、x+2=0,解得x=﹣2,故A正确; B、2﹣x=0,解得x=2,故B正确; C、2x=0,解得x=2,故C正确; D、=0方程无解,故D错误; 故选:D. 【点评】本题考查了分式方程的解,解方程是解题关键. 3.下列各组数据中,平均数和中位数相等的是( ) A.1,2,3,4,5 B.1,3,4,5,6 C.1,2,4,5,6 D.1,2,3,5,6 【考点】W4:中位数;W1:算术平均数. 【分析】根据平均数和中位数的概念列出算式,再进行计算即可. 【解答】解:A、平均数=(1+2+3+4+5)÷5=3; 把数据按从小到大的顺序排列:1,2,3,4,5,中位数是3,故选项正确; B、平均数=(1+3+4+5+6)÷5=3.8; 把数据按从小到大的顺序排列:1,3,4,5,6,中位数是4,故选项错误; C、平均数=(1+2+4+5+6)÷5=3.6; 把数据按从小到大的顺序排列:1,2,4,5,6,中位数是4,故选项错误; D、平均数=(1+2+3+5+6)÷5=3.4; 把数据按从小到大的顺序排列:1,2,3,5,6,中位数是3,故选项错误. 故选:A. 【点评】此题考查了中位数与平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.找中位数的时候一定要先按大小排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数. 4.二次函数y=﹣(x﹣2)2﹣3的图象的顶点坐标是( ) A.(2,3) B.(2,﹣3) C.(﹣2,3) D.(﹣2,﹣3) 【考点】H3:二次函数的性质. 【分析】根据题目中函数的解析式直接得到此二次函数的顶点坐标. 【解答】解:∵y=﹣(x﹣2)2﹣3, ∴二次函数y=﹣(x﹣2)2﹣3的图象的顶点坐标是(2,﹣3) 故选B. 【点评】本题考查二次函数的性质,解题的关键是明确题意,找出所求问题需要的条件. 5.以一个面积为1的三角形的三条中位线为三边的三角形的面积为( ) A.4 B.2 C. D. 【考点】KX:三角形中位线定理. 【分析】根据三角形的中位线定理得出两个三角形相似,即可得出结果. 【解答】解:根据三角形中位线定理得:两个三角形相似,相似比为,面积比为, ∴一个面积为1的三角形的三条中位线为三边的三角形的面积为; 故选:C. 【点评】本题主要考查了三角形中位线定理、相似三角形的判定与性质;熟练掌握三角形中位线定理是解决问题的关键. 6.已知点A(4,0),B(0,3),如果⊙A的半径为1,⊙B的半径为6,则⊙A与⊙B的位置关系是( ) A.内切 B.相交 C.外切 D.外离 【考点】MJ:圆与圆的位置关系;D5:坐标与图形性质. 【分析】由点A(4,0),B(0,3),可求得AB的长,又由⊙A与⊙B的半径分别为:1与6,即可根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系得出两圆位置关系. 【解答】解:∵点A(4,0),B,0,3), ∴AB==5, ∵⊙A与⊙B的半径分别为:1与6, ∴半径差为:6﹣1=5, ∴这两圆的位置关系是:内切. 故选A. 【点评】此题考查了圆与圆的位置关系.注意掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系是解此题的关键. 二、填空题(本大题共12小题,每小题4分,共48分) 7.计算:(x2)3= x6 . 【考点】47:幂的乘方与积的乘方. 【分析】根据幂的乘方,底数不变,指数相乘,进行计算. 【解答】解:原式=x2×3=x6. 故答案为x6. 【点评】此题考查了幂的乘方的性质. 8.因式分解:x2﹣4y2= (x+2y)(x﹣2y) . 【考点】54:因式分解﹣运用公式法. 【分析】直接运用平方差公式进行因式分解. 【解答】解:x2﹣4y2=(x+2y)(x﹣2y). 【点评】本题考查了平方差公式分解因式,熟记公式结构是解题的关键.平方差公式:a2﹣b2 =(a+b)(a﹣b). 9.不等式组的解集是 ﹣≤x<2 . 【考点】CB:解一元一次不等式组. 【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集. 【解答】解:解不等式x﹣2<0,得:x<2, 解不等式2x+1≥0,得:x≥﹣, ∴不等式组的解集为﹣≤x<2, 故答案为:﹣≤x<2. 【点评】本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间. 10.方程=2的解是 x=或x=﹣ . 【考点】AG:无理方程. 【分析】方程两边平方,整理后开方即可求出解. 【解答】解:两边平方得:x2﹣2=4, 解得:x=或x=﹣, 经检验x=或x=﹣是原方程的解. 故答案为:x=或x=﹣ 【点评】此题考查了无理方程,无理方程注意要检验. 11.关于x的一元二次方程2x2﹣3x+m=0有两个相等的实数根,则实数m= . 【考点】AA:根的判别式. 【分析】直接利用根的判别式得出b2﹣4ac=9﹣8m=0,即可得出答案. 【解答】解:∵关于x的一元二次方程2x2﹣3x+m=0有两个相等的实数根, ∴b2﹣4ac=9﹣8m=0, 解得:m=. 故答案为:. 【点评】此题主要考查了根的判别式,正确掌握判别式的符号是解题关键. 12.某个工人要完成3000个零件的加工,如果该工人每小时能加工x个零件,那么完成这批零件的加工需要的时间是 小时. 【考点】32:列代数式. 【分析】根据工作总量=工作时间×工作效率,计算即可得到结果. 【解答】解:根据题意得:完成这批零件的加工需要的时间是小时, 故答案为: 【点评】此题考查了列代数式,弄清题意是解本题的关键. 13.已知二次函数的图象经过点(1,3)和(3,3),则此函数图象的对称轴与x轴的交点坐标是 (2,0) . 【考点】HA:抛物线与x轴的交点. 【分析】直接利用二次函数的图象经过点(1,3)和(3,3),得出二次函数的对称轴,进而得出此函数图象的对称轴与x轴的交点坐标. 【解答】解:∵二次函数的图象经过点(1,3)和(3,3), ∴抛物线的对称轴为:x==2, 故此函数图象的对称轴与x轴的交点坐标是:(2,0). 故答案为:(2,0). 【点评】此题主要考查了抛物线与x轴的交点,正确得出对称轴是解题关键. 14.从1到10这10个正整数中任取一个,该正整数恰好是3的倍数的概率是 . 【考点】X4:概率公式. 【分析】让1到10中3的倍数的个数除以数的总个数即为所求的概率. 【解答】解:1到10中,3的倍数有3,6,9三个, 所以正整数恰好是3的倍数的概率是, 故答案为:. 【点评】本题主要考查了概率公式,用到的知识点为:概率等于所求情况数与总情况数之比. 15.正八边形一个内角的度数为 135° . 【考点】L3:多边形内角与外角. 【分析】首先根据多边形内角和定理:(n﹣2)•180°(n≥3且n为正整数)求出内角和,然后再计算一个内角的度数. 【解答】解:正八边形的内角和为:(8﹣2)×180°=1080°, 每一个内角的度数为×1080°=135°. 故答案为:135°. 【点评】此题主要考查了多边形内角和定理,关键是熟练掌握计算公式:(n﹣2)•180 (n≥3)且n为整数). 16.在平面直角坐标系中,点A(2,0),B(0,﹣3),若=,则点C的坐标为 (2,﹣3) . 【考点】LM:*平面向量;D1:点的坐标. 【分析】根据平面向量的平行四边形的法则解答即可得. 【解答】解:如图, ∵=, ∴过点A作y轴的平行线,过点B作x中的平行线,交于点C,则点C(2,﹣3), 故答案为:(2,﹣3). 【点评】本题主要考查平面向量,熟练掌握平面向量的平行四边形法则是解题的关键. 17.如图,梯形ABCD中,AD∥BC,∠A=90°,它恰好能按图示方式被分割成四个全等的直角梯形,则AB:BC= :1 . 【考点】LI:直角梯形;LH:梯形. 【分析】如图连接EC,设AB=a,BC=b则CD=2b.只要证明∠D=60°,根据sin60°=,即可解决问题. 【解答】解:如图连接EC,设AB=a,BC=b则CD=2b. 由题意四边形ABCE是矩形, ∴CE=AB=a,∠A=∠AEC=∠CED=90°, ∵∠BCF=∠DCF=∠D, 又∵∠BCF+∠DCF+∠D=180°, ∴∠D=60°, ∴sinD==, ∴=, ∴==, ∴AB:BC=:1 故答案为:1. 【点评】本题考查直角梯形的性质,锐角三角函数等知识,解题的关键是理解题意,利用角相等这个信息解决问题,发现特殊角是解题的突破口,属于中考常考题型. 18.如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是 9+2 . 【考点】PB:翻折变换(折叠问题);LB:矩形的性质. 【分析】由折叠的性质得,AB=AM,AN=AD,设AB=x,则AD=x+2,AC=x+3,根据勾股定理列方程即可得到结论. 【解答】解:由折叠的性质得,AB=AM,AN=AD, ∴AD﹣AB=AN﹣AM=MN=2, 设AB=x,则AD=x+2,AC=x+3, ∵四边形ABCD是矩形, ∴∠D=90°,CD=AB, ∴AD2+CD2=AC2,即(x+2)2+x2=(x+3)2, ∴x=1+(负值舍去), ∴AB=1+,AD=3+, ∴S矩形ABCD=(1+)(3+)=9+2; 故答案为:9+2. 【点评】本题主要考查了折叠的性质、矩形的性质、勾股定理等,综合运用各定理是解答此题的关键. 三、解答题(本大题共7小题,共78分) 19.(10分)(2017•黄浦区二模)计算:(﹣1)0+|﹣2|+()﹣1﹣2sin30°. 【考点】79:二次根式的混合运算;6E:零指数幂;6F:负整数指数幂;T5:特殊角的三角函数值. 【分析】利用零指数幂、负整数指数幂和特殊角的三角函数值进行计算. 【解答】解:原式=1+2﹣+﹣2× =2﹣++1﹣1 =2. 【点评】本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍. 20.(10分)(2017•黄浦区二模)解分式方程:. 【考点】B3:解分式方程. 【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解. 【解答】解:去分母得:(x+2)2﹣16=x﹣2, 整理得:x2+3x﹣10=0,即(x﹣2)(x+5)=0, 解得:x=2或x=﹣5, 经检验x=2是增根,分式方程的解为x=﹣5. 【点评】此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根. 21.(10分)(2017•黄浦区二模)如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E. (1)求∠CDE的度数; (2)求CE:EA. 【考点】KO:含30度角的直角三角形;KP:直角三角形斜边上的中线. 【分析】(1)根据直角三角形斜边上中线得出CD=AD=BD,求出∠DCA=∠A=15°,求出∠BDC= ∠A+∠DCA=30°,即可得出答案; (2)根据线段垂直平分线性质求出BE=AE,求出CE和BE的比,即可得出答案. 【解答】解:(1)∵在△ABC中,∠ACB=90°,D是边AB的中点, ∴CD=AD=BD, ∴∠DCA=∠A, ∵∠A=15°, ∴∠DCA=15°, ∴∠BDC=∠A+∠DCA=30°, ∵ED⊥AB, ∴∠EDB=90°, ∴∠CDE=90°﹣30°=60°; (2) 连接BE, ∵D为AB中点,DE⊥AB, ∴BE=AE, ∴∠EBA=∠A=15•, ∴∠BEC=15°+15°=30°, ∴cos30°=, ∵AE=BE, ∴=. 【点评】本题考查了直角三角形斜边上中线性质,线段垂直平分线性质,解直角三角形等知识点,能综合运用知识点进行推理是解此题的关键. 22.(10分)(2017•黄浦区二模)小明家买了一台充电式自动扫地机,每次完成充电后,在使用时扫地机会自动根据设定扫地时间,来确定扫地的速度(以使每次扫地结束时尽量把所储存的电量用完),如图是“设定扫地时间”与“扫地速度”之间的函数图象(线段AB),其中设定扫地时间为x分钟,扫地速度为y平方分米/分钟. (1)求y关于x的函数解析式; (2)现在小明需要扫地机完成180平方米的扫地任务,他应该设定的扫地时间为多少分钟? 【考点】FH:一次函数的应用. 【分析】(1)设AB的解析式为y=kx+b,把A(20,500),B(100,100)代入解方程组即可. (2)设他应该设定的扫地时间为x分钟.由题意=﹣5x+600,解方程即可. 【解答】解:(1)设AB的解析式为y=kx+b,把A(20,500),B(100,100)代入 得到, 解得, ∴y=﹣5x+600. (2)设他应该设定的扫地时间为x分钟. 由题意=﹣5x+600, 整理得x2﹣120x+3600=0, ∴x=60, 经检验x=60是分式方程的解. ∴他应该设定的扫地时间为60分钟. 【点评】本题考查一次函数的应用、分式方程的解等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会构建方程解决实际问题,注意解分式方程必须检验. 23.(12分)(2017•黄浦区二模)如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H. (1)求证:CE=CF; (2)当E为弧中点时,求证:BE2=CE•CB. 【考点】S9:相似三角形的判定与性质;L8:菱形的性质;M5:圆周角定理. 【分析】(1)连接AE,AF,由四边形ABCD是菱形,得到∠ACB=∠ACF,根据等腰三角形的性质得到∠AEC=∠ACE=∠ACF=∠AFC,推出∠EAC=∠FAC,即可得到结论; (2)由E为弧中点,得到∠CAE=∠BAE,根据等腰三角形的性质和三角形的外角的性质得到∠ACE=∠AEC=∠BAC=∠B+∠BAE,得到BE=AE=AC,根据相似三角形的性质即可得到结论. 【解答】(1)证明:连接AE,AF, ∵四边形ABCD是菱形, ∴∠ACB=∠ACF, ∵AE=AC=AF, ∴∠AEC=∠ACE=∠ACF=∠AFC, ∴∠EAC=180°﹣∠AEC﹣∠ACE, ∠CAF=180°﹣∠ACF﹣∠AFC, ∴∠EAC=∠FAC, ∴, ∴CE=CF; (2)解:∵E为弧中点, ∴∠CAE=∠BAE, ∵AB=BC,AE=AC, ∴∠ACE=∠AEC=∠BAC=∠B+∠BAE, ∴∠B=∠BAE, ∴BE=AE=AC, ∴△ABC∽△CAE, ∴, ∴AC2=BC•CE, 即BE2=CE•CB. 【点评】本题考查了相似三角形的判定和性质,菱形的性质,圆心角,弧,弦的关系,正确的作出辅助线是解题的关键. 24.(12分)(2017•黄浦区二模)如图,点A在函数y=(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=图象于点B,C,直线BC与坐标轴的交点为D,E. (1)当点C的横坐标为1时,求点B的坐标; (2)试问:当点A在函数y=(x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由. (3)试说明:当点A在函数y=(x>0)图象上运动时,线段BD与CE的长始终相等. 【考点】GB:反比例函数综合题. 【分析】(1)由条件可先求得A点坐标,从而可求得B点纵坐标,再代入y=可求得B点坐标; (2)可设出A点坐标,从而可表示出C、B的坐标,则可表示出AB和AC的长,可求得△ABC的面积; (3)可证明△ABC∽△EFC,利用(2)中,AB和AC的长可表示出EF,可得到BG=EF,从而可证明△DBG≌△CFE,可得到DB=CF. 【解答】解: (1)∵点C在y=的图象上,且C点横坐标为1, ∴C(1,1), ∵AC∥y轴,AB∥x轴, ∴A点横坐标为1, ∵A点在函数y=(x>0)图象上, ∴A(1,4), ∴B点纵坐标为4, ∵点B在y=的图象上, ∴B点坐标为(,4); (2)设A(a,),则C(a,),B(,), ∴AB=a﹣=a,AC=﹣=, ∴S△ABC=AB•AC=××=, 即△ABC的面积不发生变化,其面积为; (3)如图,设AB的延长线交y轴于点G,AC的延长线交x轴于点F, ∵AB∥x轴, ∴△ABC∽△EFC, ∴=,即=, ∴EF=a, 由(2)可知BG=a, ∴BG=EF, ∵AE∥y轴, ∴∠BDG=∠FCE, 在△DBG和△CFE中 ∴△DBG≌△CEF(AAS), ∴BD=EF. 【点评】本题为反比例函数的综合应用,涉及函数图象的交点、平行线的性质、三角形的面积、相似三角形的判定和性质、全等三角形的判定和性质等知识.要(1)中求得A点坐标是解题的关键,在(2)中用a表示出AB、AC的长是解题的关键,在(3)中证得BG=EF,构造三角形全等是解题的关键.本题考查知识点较多,综合性较强,难度适中. 25.(14分)(2017•黄浦区二模)已知:Rt△ABC斜边AB上点D,E,满足∠DCE=45°. (1)如图1,当AC=1,BC=,且点D与A重合时,求线段BE的长; (2)如图2,当△ABC是等腰直角三角形时,求证:AD2+BE2=DE2; (3)如图3,当AC=3,BC=4时,设AD=x,BE=y,求y关于x的函数关系式,并写出定义域. 【考点】KY:三角形综合题. 【分析】(1)如图1,根据勾股定理得到AB=2,过B作BF∥AC交CE的延长线于F,得到∠F=∠ACE,根据相似三角形的性质即可得到结论; (2)作AF⊥AB,使AF=BE,连接DF,根据SAS证得△CAF≌△CBE和△CDF≌△CDE,再由勾股定理和等量代换即可解答; (3)如图3,作△BCE≌△FCE,△GCD≌△ACD,延长DG交EF于H,由∠HFG=∠B,∠HGF=∠CGD=∠A,∠A+∠B=90°,得到∠DHF=90°,根据勾股定理即可得到结论. 【解答】解:(1)如图1,∵∠ACB=90°,BC=,AC=1, ∴AB=2, 过B作BF∥AC交CE的延长线于F, ∴∠F=∠ACE, ∵∠BCA=90°,∠DCE=45°, ∴∠BCE=∠DCE, ∴∠BCE=∠F, ∴BF=BC=, ∵△BEF∽△AEC, ∴=, ∴BE=2﹣; (2)证明:过点A作AF⊥AB,使AF=BE,连接DF,CF, ∵在△ABC中,AC=BC,∠ACB=90°, ∴∠CAB=∠B=45°, ∴∠FAC=45°, ∴△CAF≌△CBE(SAS), ∴CF=CE, ∠ACF=∠BCE, ∵∠ACB=90°,∠DCE=45°, ∴∠ACD+∠BCE=∠ACB﹣∠DCE=90°﹣45°=45°, ∵∠ACF=∠BCE, ∴∠ACD+∠ACF=45°, 即∠DCF=45°, ∴∠DCF=∠DCE, 又∵CD=CD, ∴△CDF≌△CDE(SAS), ∴DF=DE, ∵AD2+AF2=DF2, ∴AD2+BE2=DE2; (3)如图3,作△BCE≌△FCE,△GCD≌△ACD,延长DG交EF于H, ∵∠HFG=∠B,∠HGF=∠CGD=∠A,∠A+∠B=90°, ∴∠DHF=90°, ∵FG=1,∠B=∠F, ∴HF=,HG=, ∵EH2+HD2=ED2, ∴(y﹣)2+(x+)2=(5﹣x﹣y)2, ∴y=(0≤x≤). 【点评】本题属于三角形综合题,主要考查了相似三角形的判定与性质,等腰三角形的性质,勾股定理以及解直角三角形的综合应用,解决问题的关键是中辅助线构造直角三角形,根据勾股定理以及面积法进行求解.查看更多