- 2021-05-10 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浦东新区中考数学二模试卷及答案
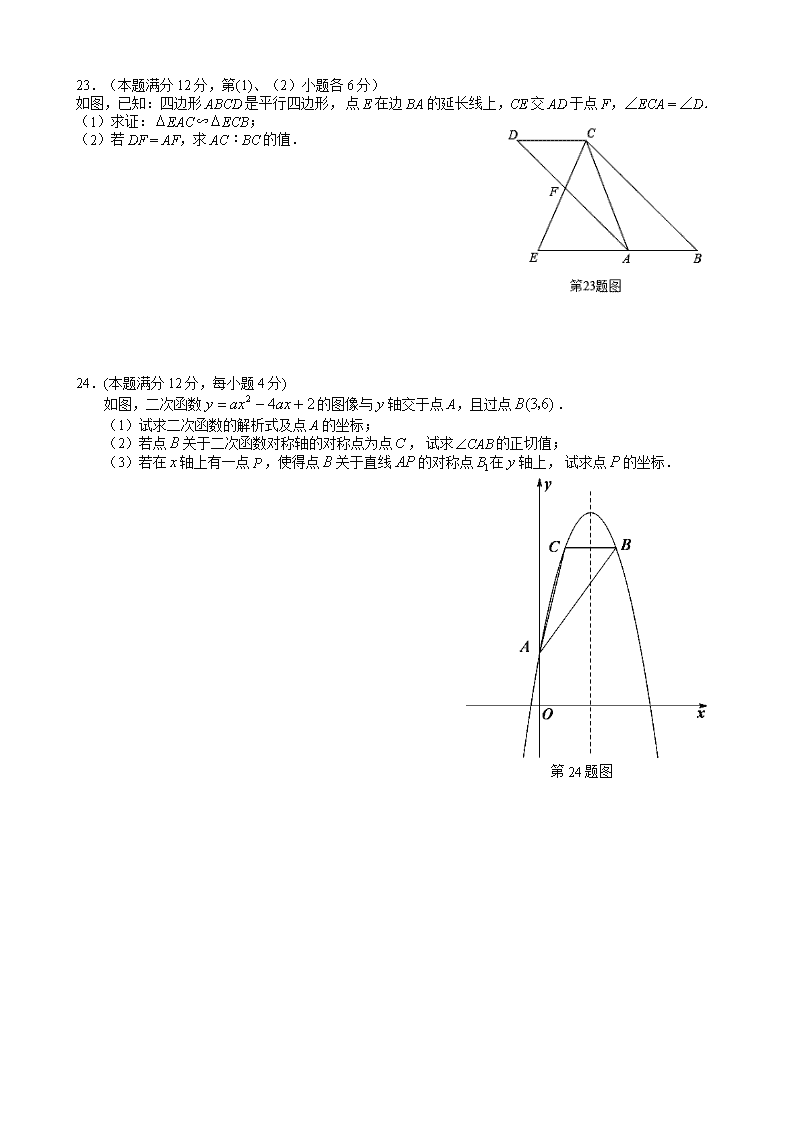
浦东新区2015学年第二学期初三教学质量检测 数学试卷 (满分150分,考试时间100分钟) 一、选择题:(本大题共6题,每题4分,满分24分) 1.2016的相反数是( ) (A); (B)-2016 ; (C) ; (D)2016. 2.已知一元二次方程,下列判断正确的是( ) (A)该方程无实数解; (B)该方程有两个相等的实数解; (C)该方程有两个不相等的实数解; (D)该方程解的情况不确定. 3.下列函数的图像在每一个象限内,随着的增大而增大的是( ) (A); (B) ; (C) ; (D). 4.如果从1、2、3这三个数字中任意选取两个数字组成一个两位数,那么这个两位数是素数的概率等于( ) (A); (B); (C); (D). A B C M N 第6题图 5.下图是上海今年春节七天最高气温(℃)的统计结果: 这七天最高气温的众数和中位数是( ) (A) 15,17; (B)14,17; (C)17,14; (D)17,15. 6.如图,△ABC和△AMN都是等边三角形,点M是△ABC的重心,那么的值为( ) (A); (B); (C); (D). 二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:= . 8.不等式的解集是 . 9.分解因式: . 10.计算: . 11.方程的解是 . 12.已知函数,那么 . 13.如图,传送带和地面所成的斜坡的坡度为1:,它把物体从地面送到离地面9米高的地方,则物体从A到B所经过的路程为 米. 14.正八边形的中心角等于 度. 15.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间不少于6小时的人数是 . 16.已知:⊙O1、⊙O2的半径长分别为2和R,如果⊙O1与⊙O2相切,且两圆的圆心距d=3,则R的值为 . 17.定义运算“﹡”:规定x﹡y(其中a、b为常数),若1﹡1=3,1﹡=1,则1﹡2= . 18.在Rt△ABC中,∠ACB=90°,BC=15,AC=20.点D在边AC上,DE⊥AB,垂足为点E,将 △ADE沿直线DE翻折,翻折后点A的对应点为点P,当∠CPD为直角时,AD的长是 . 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)计算:. 20.(本题满分10分) 解方程:. 21.(本题满分10分)如图,AB是⊙O的弦,C是AB上一点,∠AOC=90°,OA=4,OC=3,求弦AB的长. 22.(本题满分10分,每小题5分) 某工厂生产一种产品,当生产数量不超过40吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系式如图所示: (1)求y关于x的函数解析式,并写出它的定义域; (2)当生产这种产品的总成本为210万元时,求该产品的生产数量. (注:总成本=每吨的成本×生产数量) 23.(本题满分12分,第(1)、(2)小题各6分) 如图,已知:四边形ABCD是平行四边形, 点E在边BA的延长线上,CE交AD于点F,∠ECA = ∠D. (1)求证:EAC∽ECB; (2)若DF = AF,求AC︰BC的值. 24.(本题满分12分,每小题4分) 如图,二次函数的图像与轴交于点A,且过点. (1)试求二次函数的解析式及点A的坐标; (2)若点关于二次函数对称轴的对称点为点, 试求的正切值; (3)若在轴上有一点,使得点关于直线的对称点在轴上, 试求点的坐标. 第24题图 25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分) 如图,Rt△中,,,点为斜边的中点,点为边上的一个动点.联结,过点作的垂线与边交于点,以为邻边作矩形. (1)如图1,当,点在边上时,求DE和EF的长; (2)如图2,若,设,矩形的面积为,求y关于的函数解析式; 第25题 图1 (3)若,且点恰好落在Rt△的边上,求的长. 第25题 图2 浦东新区2015学年第二学期初三教学质量检测 数学试卷参考答案及评分标准 一、选择题:(本大题共6题,每题4分,满分24分) 1.B 2.C 3.A 4.A 5.C 6.B 二、填空题:(本大题共12题,每题4分,满分48分) 7. 8. 9. 10. 11. 12. 3 13. 18 14.45 15. 720. 16. 1或5 17.4 18. 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分) 解:原式=……………………………………(8分) =1+……………………………………(2分) 20.(本题满分10分) 解方程: 解:去分母得:……………………………………(4分) 整理得:……………………………………(2分) 解得:,……………………………………(2分) 经检验是原方程的根,是原方程的增根………………………(1分) 原方程的根为……………………………………(1分) 21.(本题满分为10分) 解:过点O作OD⊥AB于D 在Rt△AOC中,,AC = 5……………………………………(2分) 在Rt△AOC中, ;……………………………………(2分) 在Rt△ADO中,, ……………………………………(2分) 所以,.……………………………………(1分) 因为在⊙O中,OD⊥AB, 所以AB=2AD=,……………………………………(2分) 所以AB=.……………………………………(1分) 22.(本题满分10分,每小题5分) 解: ⑴ 设函数解析式为y=kx+b,将(0,10)、(40,6)分别代入y=kx+b 得…………………………(2分) 解之得…………………………(1分) 所以y=+10(0≤x≤40)…………………………(1+1分) ⑵ 由(+11)x=210 …………………………(2分) 解得x1=30或x2=70,…………………………(1分) 由于0≤x≤40所以x=30…………………………(1分) 答:该产品的生产数量是30吨…………………………(1分) 23.(本题满分12分,第(1)、(2)小题各6分) (1)证明:因为,四边形ABCD是平行四边形,所以,∠B = ∠D,……………(2分) 因为∠ECA = ∠D,所以∠ECA = ∠B,………………(2分) 因为∠E = ∠E, 所以△ECA∽△ECB………………(2分) (2)解:因为,四边形ABCD是平行四边形,所以,CD∥AB,即:CD∥AE 所以………………(1分) 因为DF=AF,所以,CD=AE, ………………(1分) 因为四边形ABCD是平行四边形,所以,AB=CD,所以AE=AB,所以,BE=2AE, …(1分) 因为△ECA∽△EBC 所以………………(1分) 所以,即:………………(1分) 所以.………………(1分) 24.(1) 将点代入解析式, 可得: ,解之得………………(2分) 所以二次函数解析式为.………………(1分) 点A的坐标为(0,2).………………(1分) (2)由题意, , , , . ………………(1分) 过点作于点.∴, , ………………(2分) ∴.………………(1分) (3) 由题意, , 从而点的坐标为或.………………(2分) ① 若点, 设, 由, 有, 解得: , 即………………(1分) ② 若点, 设, 由, 有, 解得: , 即………………(1分) 综合知, 点的坐标为或. 25.(1) 如图, ∵ ∴.………………(2分) ∴. 即.………………(2分) (2)过点作于点, 从而. 易得△∽△, 由, 可得, . ………………(3分) 所以. ………………(1分) ∴.………………(1分) (3) 由题意,点可以在边或者上. ①如左图 若点在边上, 从而由,可知, 于是;……(2分) ②如右图, 若点在边上. 记, 矩形边长, 由△∽△, 可得, 即, 化简可得, 因式分解后有:, 即. 而由△∽△, 所以, 从而.………………(3分) 综上知,AC的值为9或12.查看更多