北京区中考数学二模分类汇编及答案——代几综合新定义
(东城)
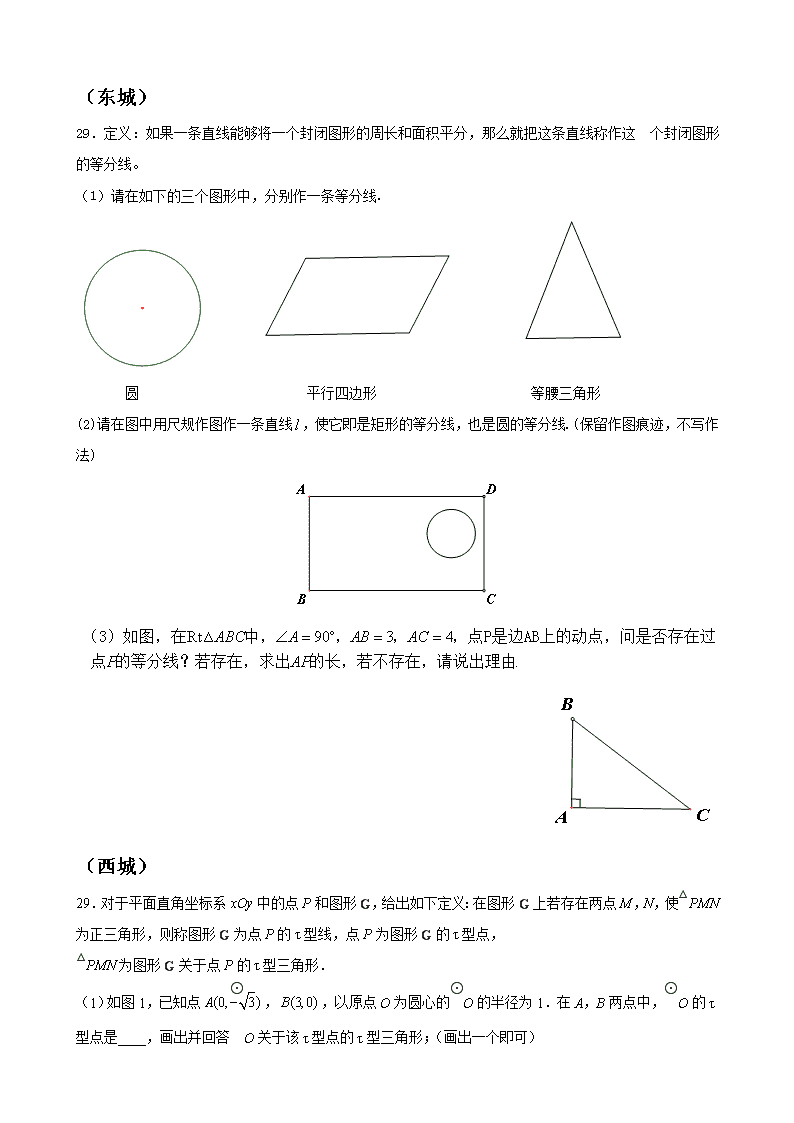
29.定义:如果一条直线能够将一个封闭图形的周长和面积平分,那么就把这条直线称作这 个封闭图形的等分线。
(1)请在如下的三个图形中,分别作一条等分线.
圆 平行四边形 等腰三角形
(2)请在图中用尺规作图作一条直线,使它即是矩形的等分线,也是圆的等分线.(保留作图痕迹,不写作法)
(西城)
29.对于平面直角坐标系xOy中的点P和图形G,给出如下定义:在图形G上若存在两点M,N,使△PMN为正三角形,则称图形G为点P的τ型线,点P为图形G的τ型点,
△PMN为图形G关于点P的τ型三角形.
(1)如图1,已知点,,以原点O为圆心的⊙O的半径为1.在A,B两点中,⊙O的τ型点是____,画出并回答⊙O关于该τ型点的τ型三角形;(画出一个即可)
(2)如图2,已知点,点(其中m>0).若线段EF为原点O的τ型线,
且线段EF关于原点O的τ型三角形的面积为,求m的值;
(3)若是抛物线的τ型点,直接写出n的取值范围.
(海淀)
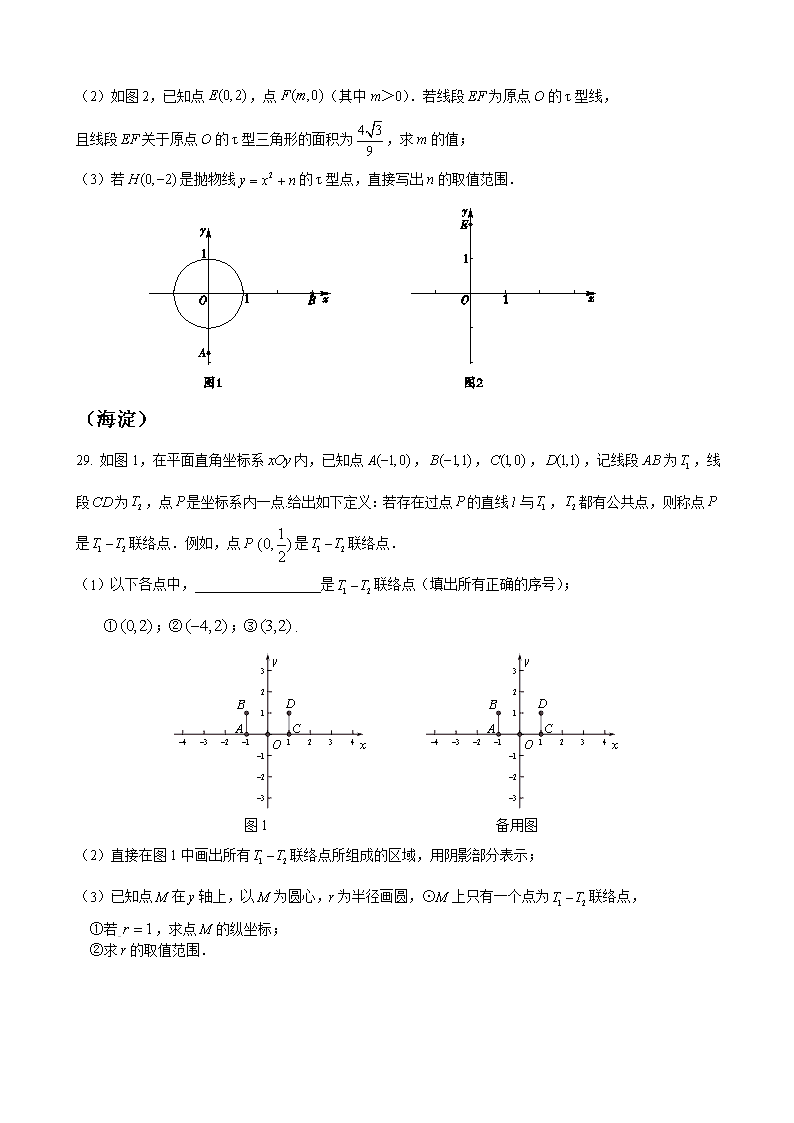
29. 如图1,在平面直角坐标系内,已知点,,,,记线段为,线段为,点是坐标系内一点.给出如下定义:若存在过点的直线l与,都有公共点,则称点是联络点.例如,点是联络点.
(1)以下各点中,__________________是联络点(填出所有正确的序号);
①;②;③.
图1 备用图
(2)直接在图1中画出所有联络点所组成的区域,用阴影部分表示;
(3)已知点M在y轴上,以M为圆心,r为半径画圆,⊙M上只有一个点为联络点,
①若,求点M的纵坐标;
②求r的取值范围.
(朝阳)
29.如图,顶点为A(-4,4)的二次函数图象经过原点(0,0),点P在该图象上,OP交其对称轴l于点M,点M、N关于点A对称,连接PN,ON.
(1)求该二次函数的表达式;
(2)若点P的坐标是(-6,3),求△OPN的面积;
(3)当点P在对称轴l左侧的二次函数图象上运动时,
请解答下面问题:
① 求证:∠PNM=∠ONM;
② 若△OPN为直角三角形,请直接写出所有符合
条件的点P的坐标.
(丰台)
29.对某一个函数给出如下定义:如果存在实数,对于任意的函数值,都满足,那么称这个函数是有上界函数,在所有满足条件的中,其最小值称为这个函数的上确界.例如,图中的函数是有上界函数,其上确界是2.
1)分别判断函数 ()和()是不是有上界函数?如果是有上界函数,求其上确界;
2)如果函数 ()的上确界是,且这个函数的最小值不超过,求的取值范围;
3)如果函数()是以3为上确界的 有上界函数,求实数的值.
(顺义)
29.如图,在平面直角坐标系xOy中,抛物线与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为,若点落在y轴上(不与点C重合),请判断以P,C,E,为顶点的四边形的形状, 并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
(昌平)
29. 在平面直角坐标系中,给出如下定义:形如与的两个二次函数的图象叫做“兄弟抛物线”.
(1)试写出一对兄弟抛物线的解析式 与 ;
(2)判断二次函数与的图象是否为兄弟抛物线,如果是,求出与的值,如果不是,请说明理由;
(3)若一对兄弟抛物线各自与轴的两个交点和其顶点构成直角三角形,其中一个抛物线的对称轴为直线且开口向上,请直接写出这对兄弟抛物线的解析式.
(石景山)
29.对于平面直角坐标系中的点,定义一种变换:作点关于轴对称的点,再将向左平移个单位得到点,叫做对点的阶“”变换.
(1)求的阶“”变换后的坐标;
(2)若直线与轴,轴分别交于两点,点的阶“”变换后得到点,求过三点的抛物线的解析式;
(3)在(2)的条件下,抛物线的对称轴与轴交于,若在抛物线对称轴上存在一点,使得以为顶点的三角形是等腰三角形,求点的坐标.
(门头沟)
29.我们给出如下定义:在平面直角坐标系xOy中,如果一条抛物线平移后得到的抛物线经过原抛物线的顶点,那么这条抛物线叫做原抛物线的过顶抛物线.
如下图,抛物线F2都是抛物线F1的过顶抛物线,设F1的顶点为A,F2的对称轴分别
交F1、F2于点D、B,点C是点A关于直线BD的对称点.
图1 图2
(1)如图1,如果抛物线y=x 2的过顶抛物线为y=ax2+bx,C(2,0),那么
① a= ,b= .
② 如果顺次连接A、B、C、D四点,那么四边形ABCD为( )
A 平行四边形 B 矩形 C 菱形 D 正方形
(2)如图2,抛物线y=ax2+c的过顶抛物线为F2,B(2,c-1).
求四边形ABCD的面积.
(3)如果抛物线的过顶抛物线是F2,四边形ABCD的面积为,
请直接写出点B的坐标.
(平谷)
29.定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”为(0,0)点有1个,即点O.
(1)“距离坐标”为(1,0)点有 个;
图1
图3
图2
[来源:Zxxk.Com]
(2)如图2,若点M在过点O且与直线CD垂直的直线l上时,点M的“距离坐标”为
(p,q),且∠BOD=120°.请画出图形,并直接写出p,q的关系式;
(3)如图3,点M的“距离坐标”为(1,),且∠AOB=30°,求OM的长.
房山
29.如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们把这样的两抛物线L1、L2互称为“友好”抛物线.
(1)一条抛物线的“友好”抛物线有_______条.
A . 1 B. 2 C. 3 D. 无数
(2)如图2,已知抛物线L3:与y轴交于点C,点C关于该抛物线对称轴的对称点为D,请求出以点D为顶点的L3的“友好”抛物线L4的表达式;
图2
(3)若抛物线的“友好”抛物线的解析式为,请直接写出与的关系式为 .
图1
怀柔
29. 阅读理解:
学习了三角形全等的判定方法:“SAS”,“ASA”,“AAS”,“SSS”和直角三角形全等的判定方法“HL”后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究.
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D.
初步探究:
如图1,已知AC=DF, ∠A=∠D,过C作CH⊥射线AM于点H,对△ABC 的CB边进行分类,可分为“CB
r,F(0,).
在Rt△AOF中,∠AOF=90°,AO=1,,
∴,.
在Rt△FEM中,∠FEM=90°,FM=FO+OM=r+,,
∴.
∴.又∵,
∴.……………………………………………………………………………………8分
朝阳
29.(1)解:设二次函数的表达式为,
把点(0,0)代入表达式,解得. ………………………………………1分
∴二次函数的表达式为,
即. ……………………………………………………………2分
(2)解:设直线OP为,
将P(-6,3)代入,解得,
∴.
当时,.
∴M(-4,2). ……………………………………………………………………3分
∵点M、N关于点A对称,
∴N(-4,6).
∴MN=4.
∴. ……………………………………………………4分
(3)①证明:设点P的坐标为,
其中,
设直线OP为,
将P代入,解得.
∴.
当时,.
∴M(-4,).
∴AN=AM==.
设对称轴l交x轴于点B,作PC⊥l于点C,
则B(-4,0),C.
∴OB=4,NB==,PC=,
NC==.
则,.
∴.
又∵∠NCP=∠NBO=90°,
∴△NCP∽△NBO.
∴∠PNM=∠ONM. …………………………………………………………………6分
② (). ………………………………………………………………8分
丰台
29. 解:(1) ()不是有上界函数;…….1分
()是有上界函数,上确界是1. …….2分
(2)∵在y=-x+2中,y随x的增大而减小,∴上确界为,即. 3分
又,所以,解得. …….4分
∵函数的最小值是,∴,得,解得.
综上所述:.…….5分
(3)函数的对称轴为.…….6分
①当时,函数的上确界是.
∴,解得,符合题意. …….7分
②当时,函数的上确界是.
∴,解得,不符合题意.
综上所述:.…….8分
顺义
29.解:
(1)∵点C(0,8)在抛物线上,
∴,................................................................................................................................1分
又∵B(6,0)在抛物线上,
∴,
∴,
∴抛物线的表达式为.......................................................................2分
(2) 结论:以P,C,E,为顶点的四边形为菱形...............................................3分
证明:∵E和关于直线PC对称,
∴∠=∠ECP,,,
又∵PE∥y轴,
∴∠EPC=∠=∠ECP,
∴EP=EC,..........................................................................................................................5分
∴,
∴四边形为菱形.................................................................................................6分
(3)∵B(6,0),C(0,8),
∴BC的表达式为.
设,则,
∴PE的长为=,
过点E作EF⊥y轴于点F,
∴△CFE∽△COB,
∴,∴,即.
由PE=EC得,解得,
∴点P的坐标为.................................................8分(不需要过程,结论正确给2分)
昌平
29.解:(1)答案不唯一,只要两个解析式给出相同的a值和相同的m值即可(每空各1分)…… 2分
(2)是兄弟抛物线,理由如下. ………………………………………………………… 3分
∵ , ……………………………………………………… 4分
, …………………………………………………… 5分
∴ 二次函数与的图象是兄弟抛物线.
此时 ,. …………………………………………………………………… 6分
(3) , ; ………………………………… 7分
或 ,. ………………………………………… 8分
石景山
29.解:(1)由阶“”变换定义:
将于轴对称的点为:…………………………………………1分
再将向左平移个单位得的坐标
……………………………………………………………………2分
(2)直线:,令∴
令∴
……………………………………………………………………3分
由阶“”变换定义:………………………………………4分
设:过三点的抛物线的解析式
将代入:
∴抛物线的解析式为:
……………………………………………………………………5分
(3),
(I)若顶角顶点,为腰,
∵
∴
,……………………………6分
(II)若为顶角顶点,为腰,
∴
……………………………………………………7分
(III)若为底,
过点作轴交抛物线对称轴于
设,,,
在中,由勾股定理
解得:∴
综上所述:点的坐标是:,,,……8分
门头沟
29.(本小题满分8分)
解:(1)① a=1,b=2.…………………………………………………………2分
② D.……………………………………………………………………3分
(2)∵ B(2,c-1),
∴ AC=2×2=4.………………………………………………………4分
∵ 当x=0,y= c,
∴ A(0,c).
∵ F1:y=ax2+c,B(2,c-1).
∴ 设F2:y=a(x-2)2+c-1.
∵ 点A(0,c)在F2上,
∴ 4a+c-1=c,
∴ .
∴ BD=(4a+c)-(c-1)=2.……………………………………………5分
∴ S四边形ABCD=4.……………………………………………………6分
(3)(,1),(,1).………………………………………8分
说明:
若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。
平谷
29.答案:(1)2;……………………………………………………………………………………1
(2)
…………………………………………………………2
过M作MN⊥AB于N
∵直线l⊥CD于O,∠BOD=120°,
∴∠MON=30°.
∵ON=p,OM=q,
∴…………………………………………………………………………………………3
(3)分别作点M关于OA、OB的对称点E、F,连接EF、OE、OF、EM、FM……………………4
∴△OEC≌△OMC,△OFD≌△OMD.
∴∠AOM=∠AOE,∠BOM=∠BOF,
OM=OE=OF.
∴∠EOF=60°.……………………………………………………5
∴OM=OE=OF=EF.
∵MD=1,MC=,
∴MF=2,ME=.
∵∠AOB=30°,
∴∠CMD=150°.…………………………………………………6
过F做FG⊥CM,交CM延长线于G,
∴∠FMG=30°.
房山
29. (1) D……………………………………………………………………………………2分
(2) 由L3:=2(x-2)2-4
∴C(0,4) ,对称轴为x=2,顶点坐标(2,-4)………………………………3分
∴点C关于对称轴x=2的对称点D(4,4)……………………………………4分
设L4:
将顶点D(4,4)代入得,
再将点(2,-4)代入得,-4=4a+4
解得:a= -2
L3的友好抛物线L4的解析式为:…………………………6分
(3) (或)………………………………………………………8分
怀柔
29. 解:(1)解:HL或AAS;……………………………1分
(2)如图:……………………………3分
(3)当BC≥CA时,也能使△ABC≌△DEF.……………………………4分
证明:
当BC=CA时,△ABC和△DEF是有一个底角相等的等腰三角形,根据AAS易证两三角形全等,当BC>CA时,在射线AM上取点B,使BC>CA,连接BC,以F为圆心,CB长为半径画弧交射线DN于点E,连接FE,则BC=EF,过点F作FG⊥DE于点G,
在△CAH和△FDG中,
∴△CAH≌△FDG(AAS),∴CH=FG,……………………………5分
在Rt△CBH和Rt△FEG中,
∴Rt△CBH≌Rt△FEG(HL),∴∠CBA=∠FED,……………………………6分
在△ABC和△EFD中,
∴△ABC≌△DEF(AAS). ……………………………8分
[来源:Z&xx&k.Com]