河南中考数学模拟题五含答案

河南中考数学模拟题五含答案

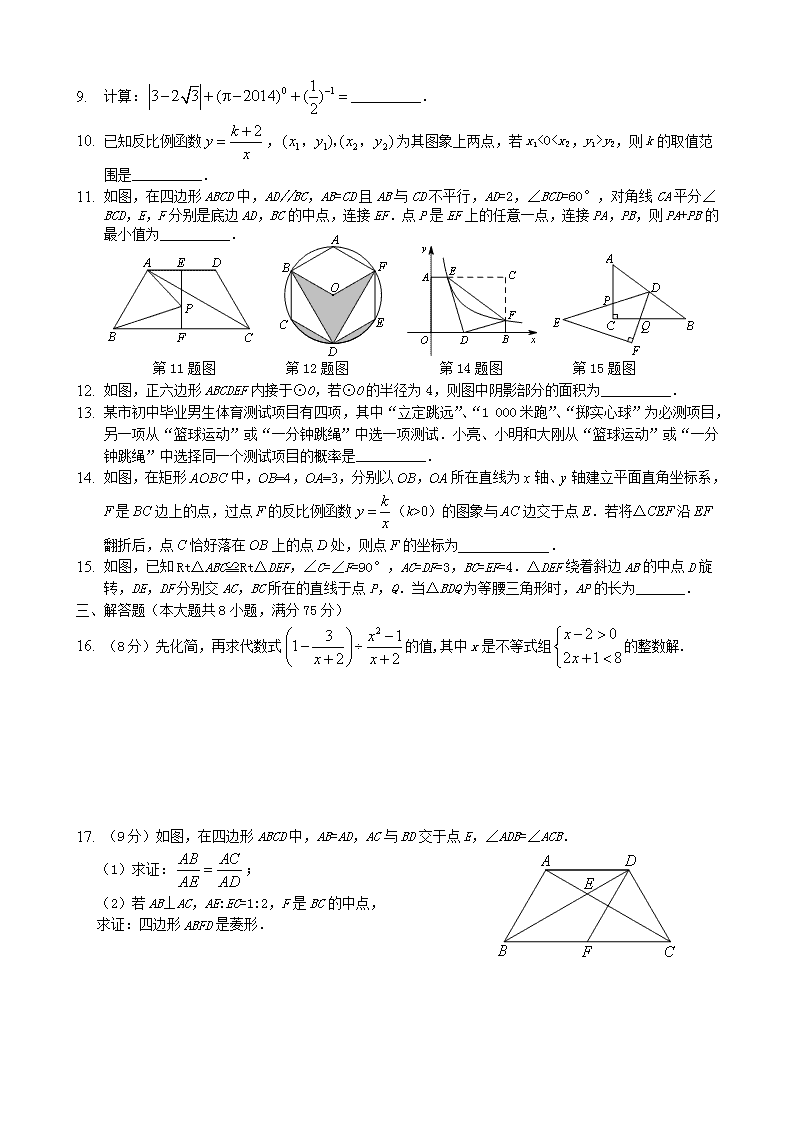
‎2017年中考数学模拟试卷（五）‎ 一、选择题（每小题3分，共24分）‎ 1. 在【 】‎ A．0~1之间 B．1~2之间 C．2~3之间 D．3~4之间 2. 下列图形中，是中心对称图形的是【 】‎ ‎ ‎ A． B． C． D． ‎ 3. 如图，是我们学过的用直尺和三角板画平行线的方法示意图，画图的原理是【 】‎ A．同位角相等，两直线平行 B． 内错角相等，两直线平行 C．两直线平行，同位角相等 D． 两直线平行，内错角相等 4. 若方程有两个实数根，则k的取值范围是【 】‎ A．k≥1 B．k≤1 C．k>1 D．k<1‎ 5. 过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图所示几何体，其展开图为【 】‎ ‎ ‎ A． B． ‎ ‎ ‎ C． D．‎ 6. 在大量重复试验中，关于随机事件发生的频率与概率，下列说法正确的是【 】‎ A． 频率就是概率 B．频率与试验次数无关 C． 概率是随机的，与频率无关 D．随着试验次数的增加，频率一般会越来越接近概率 7. 如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦．若∠ABD=58°，则∠BCD的度数为【 】A．29° B．32° C．42° D．58°‎ ‎ ‎ ‎ 第7题图 第8题图 8. 二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点(-1，0)，对称轴为直线x=2，有下列结论：①4a+b=0；②9a+c>3b；③8a+7b+2c>0；④当x>-1时，y值随x值的增大而增大．其中正确的结论有【 】‎ A．1个 B．2个 C．3个 D． 4个 二、填空题（每小题3分，共21分）‎ 1. 计算：__________．‎ 2. 已知反比例函数，为其图象上两点，若x1<0y2，则k的取值范围是__________．‎ 3. 如图，在四边形ABCD中，AD//BC，AB=CD且AB与CD不平行，AD=2，∠BCD=60°，对角线CA平分∠BCD，E，F分别是底边AD，BC的中点，连接EF．点P是EF上的任意一点，连接PA，PB，则PA+PB的最小值为__________．‎ ‎ ‎ 第11题图 第12题图 第14题图 第15题图 4. 如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为4，则图中阴影部分的面积为__________．‎ 5. 某市初中毕业男生体育测试项目有四项，其中“立定跳远”、“1 000米跑”、“掷实心球”为必测项目，另一项从“篮球运动”或“一分钟跳绳”中选一项测试．小亮、小明和大刚从“篮球运动”或“一分钟跳绳”中选择同一个测试项目的概率是__________．‎ 6. 如图，在矩形AOBC中，OB=4，OA=3，分别以OB，OA所在直线为x轴、y轴建立平面直角坐标系，F是BC边上的点，过点F的反比例函数（k>0）的图象与AC边交于点E．若将△CEF沿EF翻折后，点C恰好落在OB上的点D处，则点F的坐标为_____________．‎ 7. 如图，已知Rt△ABC≌Rt△DEF，∠C=∠F=90°，AC=DF=3，BC=EF=4．△DEF绕着斜边AB的中点D旋转，DE，DF分别交AC，BC所在的直线于点P，Q．当△BDQ为等腰三角形时，AP的长为_______．‎ 三、解答题（本大题共8小题，满分75分）‎ 8. ‎（8分）先化简，再求代数式的值,其中x是不等式组的整数解.‎ 9. 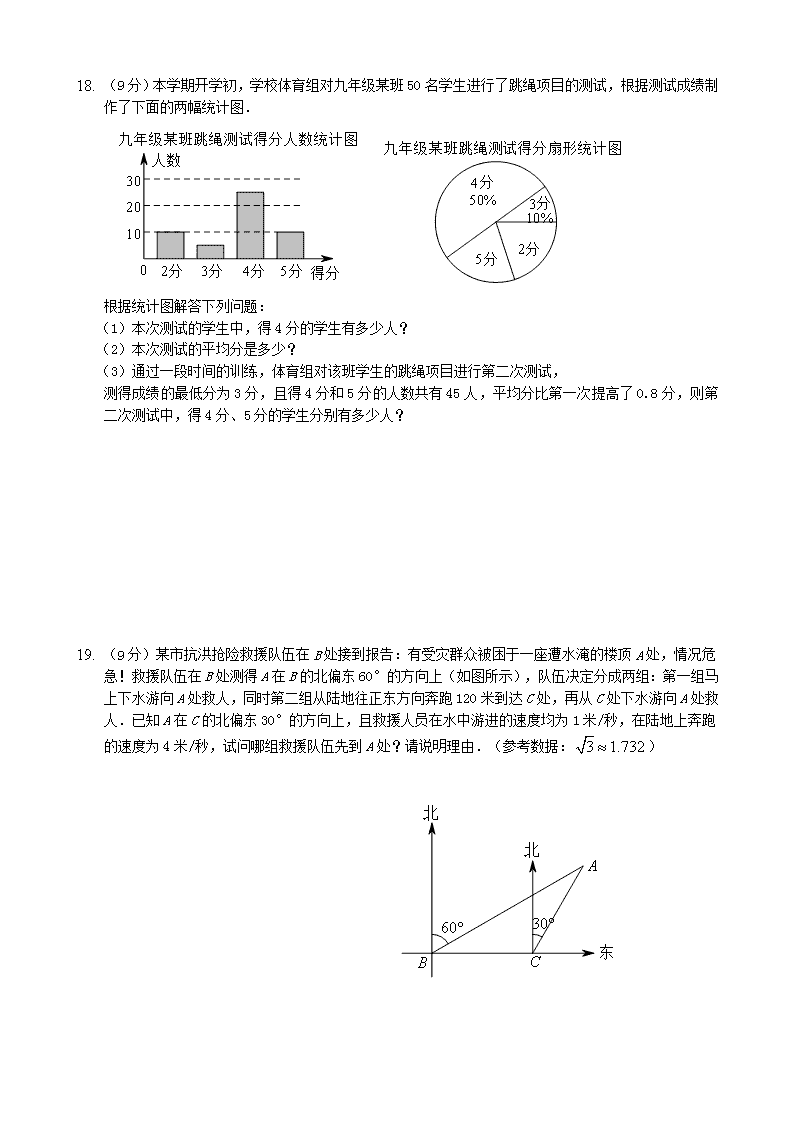‎（9分）如图，在四边形ABCD中，AB=AD，AC与BD交于点E，∠ADB=∠ACB．‎ ‎（1）求证：；‎ ‎（2）若AB⊥AC，AE:EC=1:2，F是BC的中点，‎ 求证：四边形ABFD是菱形．‎ ‎（9分）本学期开学初，学校体育组对九年级某班50名学生进行了跳绳项目的测试，根据测试成绩制作了下面的两幅统计图．‎ ‎ ‎ 根据统计图解答下列问题：‎ ‎（1）本次测试的学生中，得4分的学生有多少人？‎ ‎（2）本次测试的平均分是多少？‎ ‎（3）通过一段时间的训练，体育组对该班学生的跳绳项目进行第二次测试，‎ 测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，则第二次测试中，得4分、5分的学生分别有多少人？‎ 1. ‎（9分）某市抗洪抢险救援队伍在B处接到报告：有受灾群众被困于一座遭水淹的楼顶A处，情况危急！救援队伍在B处测得A在B的北偏东60°的方向上（如图所示），队伍决定分成两组：第一组马上下水游向A处救人，同时第二组从陆地往正东方向奔跑120米到达C处，再从C处下水游向A处救人．已知A在C的北偏东30°的方向上，且救援人员在水中游进的速度均为1米/秒，在陆地上奔跑的速度为4米/秒，试问哪组救援队伍先到A处？请说明理由．（参考数据：）‎ ‎（9分）如图，已知一次函数y=2x+2的图象与y轴交于点B，与反比例函数的图象的一个交点为A(1，m)．过点B作AB的垂线BD，与反比例函数（）的图象交于点D(n，-2)．‎ ‎（1）和的值分别是多少？‎ ‎（2）直线AB，BD分别交x轴于点C，E，若F是y轴上一点，且满足 ‎△BDF∽△ACE，求点F的坐标．‎ 1. ‎（10分）某镇水库的可用水量为12 000万立方米，假设年降水量不变，能维持该镇16万人20年的用水量．为实施城镇化建设，新迁入了4万人后，水库只能维持居民15年的用水量．‎ ‎（1）该镇年降水量以及每人年平均用水量分别是多少立方米？‎ ‎（2）政府号召节约用水，希望将水库的使用年限提高到25年，则该镇居民人均每年需节约多少立方米的水才能实现目标？‎ ‎（3）某企业投入1 000万元购买设备，每天能淡化5 000立方米海水，淡化率为70%．每淡化1立方米海水所需的费用为1.5元，政府补贴0.3元．企业将淡化水以3.2元/立方米的价格出售，每年还需各项支出40万元．按每年实际生产300天计算，该企业至少几年后才能收回成本？（结果精确到个位）‎ 2. ‎（10分）如图，在△ABC中，∠B=45°，O为AC上一个动点，过O作 ‎∠POQ=135°，且∠POQ与AB交于P，与BC交于Q．‎ ‎（1）如图1，若则______． ‎ ‎（2）如图2，若求的值，写出求解过程．‎ ‎（3）如图3，若则=_____．‎ ‎（11分）如图，在平面直角坐标系中，抛物线经过点A(，0)和点B(1，)，与x轴的另一个交点为C．‎ ‎（1）求抛物线的函数表达式．‎ ‎（2）点D在对称轴的右侧，x轴上方的抛物线上，且∠BDA=∠DAC，求点D的坐标．‎ ‎（3）在（2）的条件下，连接BD，交抛物线对称轴于点E，连接AE．‎ ‎①判断四边形OAEB的形状，并说明理由；‎ ‎②F是OB的中点，M是直线BD上的一个动点，且点M与点B不重合，当∠BMF=∠MFO时，请直接写出线段BM的长．‎ ‎2017年中考数学模拟试卷（五）‎ 参考答案 一、选择题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ C B A D B D B B 二、填空题 ‎9． 10． 11． 12． ‎ ‎13． 14．(4，) 15．或或 三、解答题 ‎16．原式，当x=3时，原式=．‎ ‎17．（1）证明略； （2）证明略．‎ ‎18．（1）25；‎ ‎（2）3.7；‎ ‎（3）得4分、5分的学生分别有15、30人．‎ ‎19．第二组救援队伍先到A处；理由略．‎ ‎20．（1）=4，=-16 （2）F(0，-8)．‎ ‎21．（1）该镇年降水量为200万立方米，每人年平均用水量是50立方米；‎ ‎（2）该镇居民人均每年需节约16立方米的水才能实现目标．‎ ‎（3）该企业至少9年后才能收回成本 ‎22．（1）1；‎ ‎（2），求解过程略；‎ ‎（3）．‎ ‎23．（1） ‎ ‎（2）‎ ‎（3）①四边形OAEB为平行四边形，理由略；‎ ‎②‎ 如图,在平面直角坐标系中,抛物线y=82√5x2+bx+c经过点A(32,0)和点B(1,22√)，与x轴的另一个交点为C.‎ ‎(1)求抛物线的函数表达式；‎ ‎(2)点D在对称轴的右侧，x轴上方的抛物线上，且∠BDA=∠DAC，求点D的坐标；‎ ‎(3)在(2)的条件下，连接BD，交抛物线对称轴于点E，连接AE.‎ ‎①判断四边形OAEB的形状，并说明理由；‎ ‎②点F是OB的中点,点M是直线BD的一个动点,且点M与点B不重合,当∠BMF=13∠MFO时，请直接写出线段BM的长。‎ 考点：‎ 二次函数综合题 分析：‎ ‎（1）利用待定系数法求出抛物线的函数表达式； （2）由∠BDA=∠DAC，可知BD∥x轴，点B与点D纵坐标相同，解一元二次方程求出点D的坐标； （3）①由BE与OA平行且相等，可判定四边形OAEB为平行四边形； ②点M在点B的左右两侧均有可能，需要分类讨论．综合利用相似三角形的性质、等腰三角形的性质和勾股定理，求出线段BM的长度．‎ 解答：‎ ‎(1)将A(32,0)、B(1,22√)代入抛物线解析式y=82√5x2+bx+c，得：‎ ‎⎧⎩⎨⎪⎪⎪⎪⎪⎪82√5×94+32b+c=082√5+b+c=22√，‎ 解得：⎧⎩⎨⎪⎪b=−82√c=422√5.‎ ‎∴y=82√5x2−82√x+422√5.‎ ‎(2)当∠BDA=∠DAC时,BD∥x轴。‎ ‎∵B(1,22√)，‎ 当y=22√时,22√=82√5x2−82√x+422√5，‎ 解得：x=1或x=4，‎ ‎∴D(4,22√).‎ ‎(3)①四边形OAEB是平行四边形。‎ 理由如下：抛物线的对称轴是x=52，‎ ‎∴BE=52−1=32.‎ ‎∵A(32,0)，‎ ‎∴OA=BE=32.‎ 又∵BE∥OA，‎ ‎∴四边形OAEB是平行四边形。‎ ‎②∵O(0,0),B(1,22√),F为OB的中点,∴F(12,2√).‎ 过点F作FN⊥直线BD于点N,则FN=22√−2√=2√,BN=1−12=12.‎ 在Rt△BNF中,由勾股定理得：BF=BN2+FN2−−−−−−−−−−√=32.‎ ‎∵∠BMF=13∠MFO，∠MFO=∠FBM+∠BMF，‎ ‎∴∠FBM=2∠BMF.‎ ‎(I)当点M位于点B右侧时。‎ 在直线BD上点B左侧取一点G,使BG=BF=32，连接FG，则GN=BG−BN=1，‎ 在Rt△FNG中,由勾股定理得：FG=GN2+FN2−−−−−−−−−−√=3√.‎ ‎∵BG=BF，∴∠BGF=∠BFG.‎ 又∵∠FBM=∠BGF+∠BFG=2∠BMF,‎ ‎∴∠BFG=∠BMF，又∵∠MGF=∠MGF，‎ ‎∴△GFB∽△GMF，‎ ‎∴GMGF=GFGB,即32+BM3√=3√32，‎ ‎∴BM=12；‎ ‎(II)当点M位于点B左侧时。‎ 设BD与y轴交于点K，连接FK，则FK为Rt△KOB斜边上的中线，‎ ‎∴KF=12OB=FB=32，‎ ‎∴∠FKB=∠FBM=2∠BMF，‎ 又∵∠FKB=∠BMF+∠MFK，‎ ‎∴∠BMF=∠MFK，‎ ‎∴MK=KF=32，‎ ‎∴BM=MK+BK=32+1=52.‎ 综上所述,线段BM的长为12或52.‎