- 2021-05-10 发布 |
- 37.5 KB |
- 21页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
历届初三中考数学几何复习题
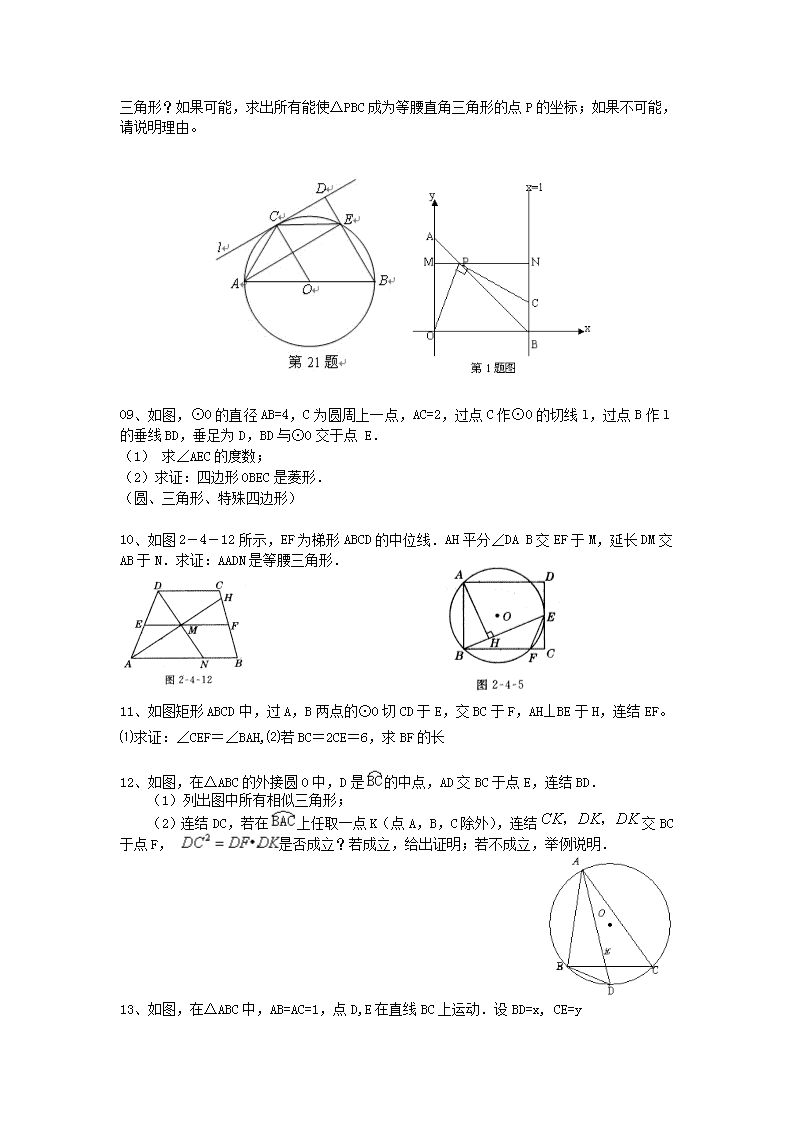
01、如图,已知⊿ABC中,AB=AC,AD⊥AB于点A,交BC边于点E,DC⊥BC于点C,与AD交于点D, (1)求证:⊿ACE ∽⊿ADC; (2)如果CE=1,CD=2,求AC的长. 02、一旅游者骑自行车沿正东方向笔直的公路BC行驶,在B地测得某建筑物A在北偏东45°方向,行驶10分钟后到达C地,测得建筑物A在北偏西60°方向.如果此旅游者的速度为12千米/时,求建筑物A到公路BC的距离(结果可保留根号). 03、“开发西部”是我国近几年的一项重要的战略决策。“攻坚”号筑路工程队在西部某地区修路过程中需要沿AB方向开山筑隧道(如图),为了加快施工进度,要在山的对面同时施工。因此,需要确定山对面的施工点。工程技术人员从AB上取一点C,测出以下数据:∠ACD的度数、CD的长度及∠D的度数。 (1)若∠ACD=135°,CD=500米,∠D=60°,试求开挖点E离开点D的距离(结果保留根号); (2)若∠ACD=,CD=m米,∠D =,试用、和m表示开挖点E离开点D的距离。(只需写出结论。) 04、如图, 点A的坐标为(0,5),点B在第一象限,⊿AOB为等边三角形,点C在x轴正半轴上. (1)以AC为边,在第一象限作等边⊿ACE(保留作图痕迹,不写作法和证明). (2)设AC与OB的交点为D,CE与AB的延长线交于F,求证:⊿ADB∽⊿AFC. (3)连结BE,试猜想∠ABE的度数,并证明你的猜想. (4)若点E的坐标为(s,t),当点C在x正半轴运动时,求s、t的关系式. E D B C A 05、如图所示,∠ACB=90°,DF⊥AB于F,sinB=,,且CE=5,求: (1)BC的长; (2) . 06、如图,已知矩形,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H. (1)求△PEF的边长; (2)求证:; (第06题图) (3)若△PEF的边EF在线段BC上移动.试猜想:PH与BE有何数量关系?并证明你猜想的结论. 07、如图,在△ABC中,∠C=90°,AC=4,BC=3,O是AB上一点,且AO:OB=2:5. (1) 过点O作OH⊥AC垂足为H,求点O到直线AC的距离OH的长;(图1) (2) 若P是边AC上的一个动点,作PQ⊥OP交线段BC于Q(不与B、C重合)(图2) ①求证:△POH∽△QPC; ②设AP=,CQ=,试求关于的函数解析式,并写出定义域; ③当AP= 时,能使△OPQ与△CPQ相似.(直接写出结果) 08、如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。 (1)当点C在第一象限时,求证:△OPM≌△PCN; (2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围; (3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC 是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。 09、如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B作l的垂线BD,垂足为D,BD与⊙O交于点 E. (1) 求∠AEC的度数; (2)求证:四边形OBEC是菱形. (圆、三角形、特殊四边形) 10、如图2-4-12所示,EF为梯形ABCD的中位线.AH平分∠DA B交EF于M,延长DM交AB于N.求证:AADN是等腰三角形. 11、如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连结EF。 ⑴求证:∠CEF=∠BAH,⑵若BC=2CE=6,求BF的长 12、如图,在△ABC的外接圆O中,D是的中点,AD交BC于点E,连结BD. (1)列出图中所有相似三角形; (2)连结DC,若在上任取一点K(点A,B,C除外),连结交BC于点F, 是否成立?若成立,给出证明;若不成立,举例说明. 13、如图,在△ABC中,AB=AC=1,点D,E在直线BC上运动.设BD=x, CE=y (l)如果∠BAC=300,∠DAE=l050,试确定y与x之间的函数关系式; (2)如果∠BAC=α,∠DAE=β,当α, β满足怎样的关系时,(l)中y与x之间的函数关系式还成立?试说明理由. 14、某社区拟筹资金2000元,计划在一块上、下底分别是10米、20米的梯形空地上种植花木(如图所示),他们想在△AMD和△BMC地带种植单价为10元/米2的太阳花,当△AMD地带种满花后,已经花了500元,请你预算一下,若继续在△BMC地带种植同样的太阳花,资金是否够用?并说明理由. 15、如图,E、F分别为矩形ABCD的边AD、BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积. 16、如图5,路边有两根电线杆相距4米,分别在高为3米的A处和6米的C处用铁丝将两杆固定,求铁丝AD与铁丝将两杆固定,求铁丝AD与铁丝BC的交点M处离地面的高MH. 17、如图,在矩形 ABCD中,AB=3 , BC =2, 点A的坐标为(1 , O ) ,以CD为直径,在矩形ABCD内作半圆,点M为圆心, 设过 A 、B 两点抛物线的解析式为 y =ax2+ bx +c. 顶点为点N . ( 1 )求过 A 、C 两点直线的解析式; ( 2 )当点 N 在半圆M内时,求a的取值范围; ( 3 )过点 A 作⊙M 的切线交 BC于点F, E为切点,当以点A 、F 、B为顶点的三角形与以点C 、N 、M 为顶点的三角形相似时,求点N的坐标. 18、若,则= ;若,且,则 = ,= ,= 。 19、若,则= 。 20、如图,在□ABCD中,E为BC上一点,BE∶EC=2∶3,AE交BD于点F,则BF∶FD= 。 21、已知如图,AB∥CD,AD与BC相交于点O,则下列比例式中正确的是( ) A、 B、 C、 D、 22、如图,在△ABC中,AD=DF=FB,AE=EG=GC,FG=4,则( ) A、DE=1,BC=7 B、DE=2,BC=6 C、DE=3,BC=5 D、DE=2,BC=8 23、如图,BD、CE是△ABC的中线,P、Q分别是BD、CE的中点,则PQ∶BC=( ) A、1∶3 B、1∶4 C、1∶5 D、1∶6 24、如图,∥,,BC=4CD,若,则=( ) A、 B、2 C、 D、4 25、已知如图,AD=DE=EC,且AB∥DF∥EH,AH交DF于K,求的值。 26、如图,□ABCD中,EF交AB的延长线于E,交BC于M,交AC于P,交AD于N,交CD的延长线于F。求证:。 27、如图,已知梯形ABCD中,AD∥BC,AB=DC=3,P为BC上一点,PE∥AB交AC于E,PF∥CD交BD于F,设PE、PF的长分别为、,。那么当点P在BC边上移动时,的值是否变化?若变化,求出的范围;若不变,求出的值,并说明理由。 3.如图,四边形ABCD中,对角线AC、BD相交于O,M、N分别为A原中点,MN交AC、BD于E、F。求证:BD·OE=AC·OF. 如图,取AB的中点G 连结GM,GN 因为M、N分别为AD,BC中点 所以GM∥BD,GM=BD GN∥AC,GN=AC 所以∠GMD=∠OFE,∠GNM=∠OEF 所以△GMN∽△OFE 所以GM:OF=GN:OE 即BD:=AC:OE 所以BC·OE=AC·OF 中考几何常见辅助线介绍 一.过角平分线上一点向角两边作垂线段,利用角平分线上的点到角两边距离相等去作题. 1.如图在四边形ABCD中,BC>BA,AD=DC,BD平分∠ABC.求证:. A D B C 2.已知:如图,在ABC中,∠A=90°,AB=AC,∠1=∠2,求证:BC=AB+AD. A B C D 1 2 3.如图,□ABCD中,E是DC上一点,F是AD上一点,AE交CF于点O,且AE=CF. 求证:OB平分. D E C B O F A 二.有和角平分线垂直的线段时,把它延长可得到中点或相等的线段,从而与三角形中位线或三角形全等建立起联系. A B C H D 1 2 4.已知:如图,∠1=∠2,AB﹥AC,CD⊥AD于D,H是BC中点, 求证:DH=(AB-AC). 5.已知:如图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE,求证:BD=2CE. A B C E D 1 2 三.有角平分线时,常作平行线,构造等腰三角形。(角平分线+平行线等腰三角形.) A B C F E D 6.已知:如图,中,D、E在BC上,且DE=EC,过D作DF∥AB,交AE于点F,DF=AC.求证:AE平分. 四、有中线时可延长中线,构造全等三角形或平行四边形: A B D C 7.已知:如图,AD为中线,求证:. A B C E N D M 8. 已知:如图,,AD=AC,AB=AE,M为BC中点,AM的延长线交DE于N.求证:. A B C E N D 9.已知:如图,的边BC的中点为N,过A的任一直线于D,于E.求证:NE=ND. 五、作斜边中线,利用斜边中线性质解题 10.如图,在中,AB=AC,,O为BC的中点. ①写出点O到的三个顶点A、B、C的距离的关系(不变证明) A M B O C N ②如果点N、M分别在线段AB、AC上移动,在移动中保证AN=BM,请判断OMN的形状,并证明你的结论. 六、有中点,造中位线 A B D C E 11.如图,在中,AD是BC边上的高,,点E为BC的中点, 求证:AB=2DE. 12.已知:如图,E、F分别为四边形ABCD的对角线中点,AB>CD.求证:. A D F E B C 七、有底中点,连中线,利用等腰三角形三线合一性质证题 13.已知:如图,矩形ABCD,E为CB延长线上一点,且AC=CE,F为AE中点, 求证:. A D C F E B 九、有中点、造中垂 14.已知:如图,在矩形ABCD中,点M是AD中点,点N是BC中点,P是CD延长线上一点,PM交AC于Q,MN交AC于O.求证:. A B N C O D P M Q 九、与梯形中点有关的辅助线:①有腰中点时,常见以下三种引辅助线法 A D F B C (1) E A D B C (2) E G A D B C (3) E E 15.已知:如图,在梯形ABCD中,AB∥CD,,M为AD中点,且. 求证:(1)BM平分,CM平分.(2). A M D C B (上海卷)已知点在线段上,点在线段延长线上.以点为圆心,为半径作圆,点是圆上的一点. (1)如图,如果,.求证:; (2)如果(是常数,且),,是,的比例中项.当点在圆上运动时,求的值(结果用含的式子表示); (3)在(2)的条件下,讨论以为半径的圆和以为半径的圆的位置关系,并写出相应的取值范围. [解] (1)证明:,. . , .,. (2)解:设,则,,是,的比例中项, , 得,即. . 是,的比例中项,即, ,. 设圆与线段的延长线相交于点,当点与点,点不重合时, ,. . ;当点与点或点重合时,可得, 当点在圆上运动时,; (3)解:由(2)得,,且, ,圆和圆的圆心距, 显然,圆和圆的位置关系只可能相交、内切或内含. 当圆与圆相交时,,得, ,; 当圆与圆内切时,,得; 当圆与圆内含时,,得. (福建龙岩卷)如图,已知抛物线与坐标轴交于三点,点的横坐标为,过点的直线与轴交于点,点是线段上的一个动点,于点.若,且. (1)确定的值:; (2)写出点的坐标(其中用含的式子表示): ; (3)依点的变化,是否存在的值,使为等腰三角形?若存在,求出所有的值;若不存在,说明理由. [解] (1) (2) (3)存在的值,有以下三种情况 ①当时 ,则 ②当时 得 ③当时,如图 解法一:过作,又 则 又 解法二:作斜边中线 则, 此时 解法三:在中有 (舍去) 又 当或或时,为等腰三角形. 福建厦门课改A卷)已知P(,)是抛物线上的点,且点P在第一象限. (1)求的值 (2)直线过点P,交轴的正半轴于点A,交抛物线于另一点M. ①当时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明; O P A M ②当时,记△MOA的面积为S,求的最大值. [解] (1) (2)①b=2a, P在直线上,则 A(2,0) M(-1,a) ∠OPA=90° 即, , P(1,1) 故存在这样的点P ② 又 ∴S= ∴当时, 5、(福建漳州卷)如图,已知矩形,在上取两点(在左边),以为边作等边三角形,使顶点在上,分别交于点. (1)求的边长; (2)在不添加辅助线的情况下,当与不重合时,从图中找出一对相似三角形,并说明理由; (第27题) (3)若的边在线段上移动.试猜想:与有何数量关系?并证明你猜想的结论. [解] (1)过作于 矩形 ,即,又 是等边三角形 1 2 3 4 在中 的边长为. (2)正确找出一对相似三角形 正确说明理由 方法一: 理由:矩形 方法二: 理由:矩形 又 (3)猜想:与的数量关系是: 1 2 3 4 5 6 7 8 证法一:在中, 是等边三角形 证法二:在中, 是等边三角形, 在中, ,即 在中, 证法三:在中, , 是等边三角形 ① 即 ② 把②代入①得, 4.已知△ABC中,AB=AC=2,AB边上的高CH为,正方形DEFG的DE边在BC上,F、G分别在AC、AB上,求:DE的长度。 (1)当∠BAC 锐角时,如图,作BC边上的高AK,交GF于M AH===1 所以AH=BH=AB,因为CH⊥AB 所以AB=AC=BC=2,所以AK= 设正方形边长为X 因为FG∥BC,所以△AGF∽△ABC 所以GF:BC=AM:AK 所以X:2=(-X): 所以X=-6 即正方形边长为-6 (2)当∠BAC为钝角时,如图,作BC边上高AK 在Rt△ACH中,AH==1 所以BH=AB+AH=3 所以Rt△BHC中, BC===2 在Rt△ABK中, AK===1 因为FG∥BC, 所以△AFG∽△ABC, 所以X=2=(1-X):1 所以X= 即正方形边长为 5.已知,如图,锐角△ABC中,AD⊥BC于D,H为垂心(三角形三条高线的交点);在AD上有一点P,且∠BPC为直角。求证:. .如图,连结GH并延长交AB开E 则CE⊥AB 所以Rt△ABD∽Rt△CHD 所以AD:CD=BD:HD, 所以AD·HD=BD·CD 又△BPD∽△PCD 所以BD:PD=PD:CD 所以PD=BD·CD 所以PD=AD·HD. 9.如图,点为直线上的两点,过两点分别作y轴的平行线交双曲线()于两点. 若,则 的值为 . (第10题) (第9题) 10.如图,在Rt△ABC中,斜边AB的长为35 ,正方形CDEF内接于△ABC,且其边长为12,则△ABC的周长为 . 11.已知:不论k取什么实数,关于x的方程(a、b是常数)的根总是x=1,试求a、b的值。 12.已知关于的一元二次方程的两个整数根恰好比方程的两个根都大1,求的值. 14如图,△ABC中,,.点P在△ABC内,且,求△ABC的面积. (第14题) 答案:10.84 11. 解:把x=1代入原方程并整理得(b+4)k=7-2a 要使等式(b+4)k=7-2a不论k取什么实数均成立,只有 解之得 , 12.解:设方程的两个根为,其中为整数,且≤,则方程的两根为,由题意得 , 两式相加得 , 即 , 所以 或 解得 或 又因为 所以 ;或者, 故,或29. 14.解:如图,作△ABQ,使得 则△ABQ∽△ACP . 由于,所以相似比为2. 于是 (第14题) . . 由知,,于是. 所以 ,从而. 于是 . 故 . 2.如图1,在正方形ABCD中,N是CD的中点,M是AD上异于D的点,且∠NMB=∠MBC,则AM:AB=( ) A.; B.; C.; D. 解.如图,延长MN交BC的延长线于T,设MB的中点为O,连TO,则△BAM∽△TOB ∴AM:MB=OB:BT ∴MB=2AM·BT (1) 令DN=1,CT=MD=k,则AM=2 – k 所以BM= BT= 2 + k代入(1),得4 + (2 – k )= 2 (2 – k ) (2 + k ) 所以 k = 所以AM:AB=:2 = 2.如图,在△ABC中,AB=2,AC=, ∠A=∠BCD=45°,求BC的长及△BDC的面积。 解:如图,作CE⊥AB于E, 则CE=AE= 所以BE=AB-AE=2 - 又 所以BC= 再过D作DF⊥BC,交CB延长线于F,并设DF=CF=x, 则BF= x – BC = x + 1 - 又Rt△DFB∽Rt△CEB, 所以DF:BF=CE:BE,即x:(x + 1 - ) = 所以x = 所以 4.若,,且满足,则的值为( ). (A)1 (B)2 (C) (D) 答案:C 6.若a是一个完全平方数,则比a大的最小完全平方数是 . 。 7.若关于的方程有三个根,且这三个根恰好可 以作为一个三角形的三条边的长,则的取值范围是 . 答案:6. 7.3<m≤4. 3、在等边三角形ABC所在的平面内存在点P,使⊿PAB、⊿PBC、⊿PAC都是等腰三角形.请指出具有这种性质的点P的个数( ) (A)1 (B)7 (C)10 (D)15 答案:C. ————总结总结(国家机密不可泄露)不要因此而放弃!! 加油吧,你会成功的,我相信你~!查看更多