2019届中考数学一轮复习 第27课时 与圆有关的位置关系导学案（无答案）

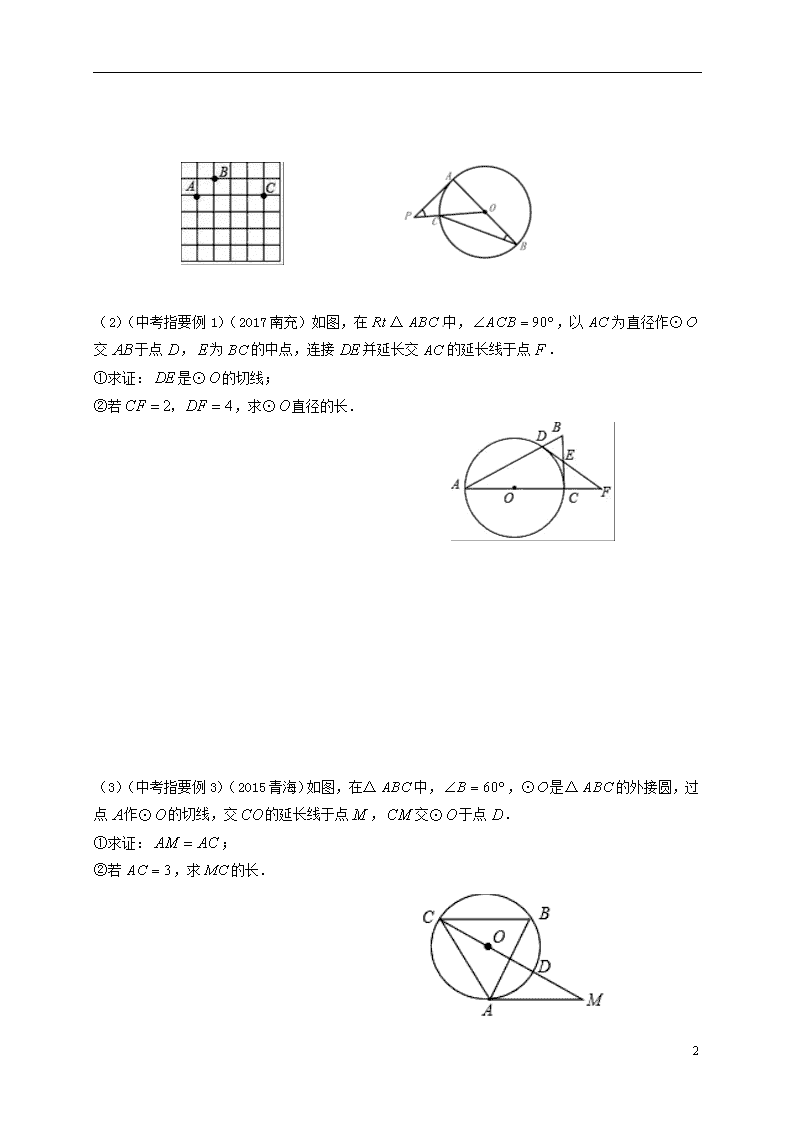
2019届中考数学一轮复习 第27课时 与圆有关的位置关系导学案（无答案）

第27课时 与圆有关的位置关系 班级： 姓名： ‎ 学习目标: 1. 探索并了解点与圆的位置关系，了解直线与圆的位置关系及三角形内切圆的概念，会判断图形的位置关系．‎ ‎2. 掌握切线的概念，探索切线与过切点的半径的关系，会用三角尺过圆上一点画圆的切线．‎ ‎3. 探索并证明切线长定理，会利用它进行证明和相关计算 重难点：灵活运用切线的性质定理和判定定理进行相关计算和证明．‎ ‎ 学习过程 一．知识梳理 ‎1.点与圆的位置关系：如果设圆的半径为r，点到圆心的距离为d，那么：‎ ‎① ⇔点在 ．‎ ‎② ⇔点在 ．‎ ‎③ ⇔点在 ．‎ ‎2.直线与圆的位置关系：如果⊙O的半径为r，圆心O到直线l的距离为d，那么：‎ ‎① ⇔ 直线与圆 ．‎ ‎② ⇔ 直线与圆 ．‎ ‎③ ⇔ 直线与圆 ．‎ ‎3.与圆有 公共点的直线叫做圆的切线，唯一的公共点叫做 ．‎ 切线的判定定理：经过半径的外端并且 于这条半径的直线是圆的切线．‎ 性质定理：圆的切线垂直于经过 的半径．‎ ‎4.在经过圆外一点的圆的切线上，这点和切点之间 的长，叫做这点到圆的切线长．‎ 切线长定理：从圆外一点引圆的两条切线，它们的切线长 ，圆心和这一点的连线 两条切线的夹角．‎ ‎5.与三角形各边 的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的 ，这个三角形叫做圆的 三角形．‎ ‎、典型例题 ‎1.点与圆的位置关系 ‎（2017宁夏）如图，点均在6×6的正方形网格格点上，过三点的外接圆除经过三点外还能经过的格点数为　 　．‎ ‎2.切线的性质与判定 ‎（1）（2017自贡）是⊙的直径，切⊙于点，交⊙于点;‎ 连接,若,则等于 （ ）‎ A.20° B.25° C. 30° D.40°‎ 5‎ ‎（2）（中考指要例1）（2017南充）如图，在△中，，以为直径作⊙交于点，为的中点，连接并延长交的延长线于点．‎ ‎①求证：是⊙的切线；‎ ‎②若，求⊙直径的长．‎ ‎（3）（中考指要例3）（2015青海）如图，在△中，，⊙是△的外接圆，过点作⊙的切线，交的延长线于点，交⊙于点．‎ ‎①求证：；‎ ‎②若，求的长．‎ 5‎ ‎3.切线长定理与内切圆 ‎（1）(2016·荆州)如图，过⊙外一点引⊙的两条切线切点分别是交⊙于点，是优弧上不与点重合的一个动点，连接.若，则的度数是( )‎ A.15°　　B. 20° C. 25°　　 D. 30°‎ ‎（2）(2017·武汉)已知一个等腰三角形三角形的底边长为10，腰长为分别13，则其内切圆的半径为 ‎ 三、中考预测 ‎（2017东营）如图，在△中，，以为直径的⊙交于点，过点作⊙的切线，交于点，的反向延长线交⊙于点．‎ ‎（1）求证：；‎ ‎（2）若，⊙的半径为10，求的长度．‎ 四、反思总结 ‎1.本节课你复习了哪些内容？‎ 5‎ ‎2.通过本节课的学习，你还有哪些困难？‎ 五、达标检测 ‎1、（2015•湘西州）⊙的半径为，点到圆心的距离，则点与圆的位置关系为（　　）‎ ‎　 A．点在圆上 B． 点在圆内 C． 点在圆外 D． 无法确定 ‎2、（2016嘉兴）如图，中，，以点为圆心的圆与相切，则⊙的半径为（ ）‎ A. 2.3 ‎‎ B.‎2.4 C.2.5 D.2.6‎ ‎3、（2016南京）如图，在矩形中，，分别与⊙相切于三点，过点作⊙的切线交于点，切点为，则的长为( ) ‎ A. B. C. D. ‎ ‎4、（2016鄂州）如图，在△中，，是的平分线，的平分线 交于点，点在上，以点为圆心，的长为半径的圆经过点，交于点，交 于点．‎ ‎ （1）求证：为⊙的切线． ‎ ‎ （2）当时，求⊙的半径．‎ ‎ （3）在（2）的条件下，求线段的长．‎ 5‎ ‎5、（中考指要例2）（2015温州）如图，是半圆的直径，于点，交半圆于点，切半圆于点。已知。‎ ‎（1）求证：∥；‎ ‎（2）若，，求的长。‎ 5‎