北师大本初中数学年中考年模拟真题演练

北师大本初中数学年中考年模拟真题演练

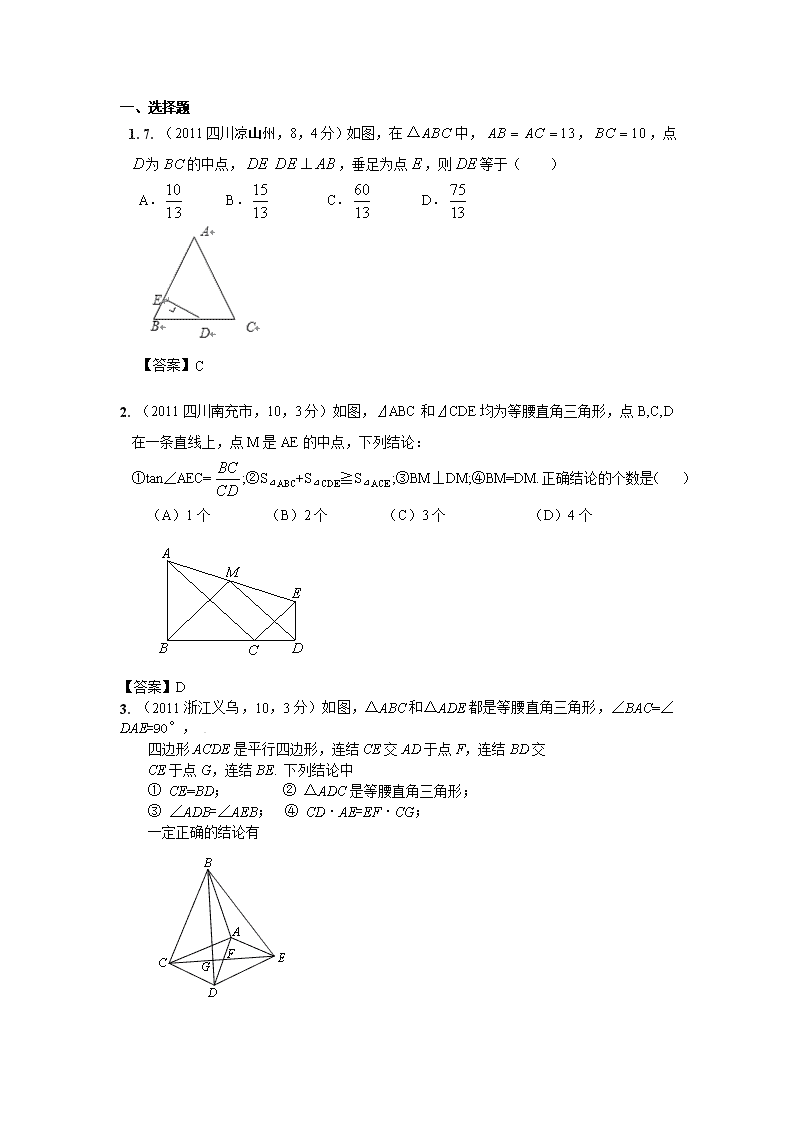
一、选择题 ‎1. 7. （2011四川凉山州，8，4分）如图，在中，，，点为的中点，，垂足为点，则等于（　　） ‎ A．　　 B． 　　C．　　 D． ‎ ‎【答案】C ‎2. （2011四川南充市，10，3分）如图，⊿ABC和⊿CDE均为等腰直角三角形，点B,C,D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=;②S⊿ABC+S⊿CDE≧S⊿ACE ;③BM⊥DM;④BM=DM.正确结论的个数是（ ）‎ ‎（A）1个 （B）2个 （C）3个 （D）4个 ‎【答案】D ‎3. （2011浙江义乌，10，3分）如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°， ‎ 四边形ACDE是平行四边形，连结CE交AD于点F，连结BD交 ‎ CE于点G，连结BE. 下列结论中 ‎① CE=BD； ② △ADC是等腰直角三角形；‎ ‎③ ∠ADB=∠AEB； ④ CD·AE=EF·CG；‎ 一定正确的结论有 A B C D E F G A．1个 B．2个 C．3个 D．4个 ‎【答案】D ‎4. （2011台湾全区，30）如图(十三)，ΔABC中，以B为圆心，长为半径画弧，分别交、‎ 于D、E两点，并连接、．若∠A=30∘，＝，则∠BDE的度数为何？‎ A． 45 B． 52．‎5 C． 67．5 D． 75‎ ‎【答案】Ｃ ‎5. （2011台湾全区，34）如图(十六)，有两全等的正三角形ABC、DEF，且D、A分别为△ABC、△DEF 的重心．固定D点，将△DEF逆时针旋转，使得A落在上，如图(十七)所示．求图(十六)与图(十 七)中，两个三角形重迭区域的面积比为何？‎ A．2：1 B． 3：‎2 C． 4：3 D． 5：4‎ ‎【答案】Ｃ ‎6. （2011山东济宁，3，3分）如果一个等腰三角形的两边长分别是‎5cm和‎6cm，那么此三角形的周长是 ‎ A．‎15cm B．‎16cm ‎ C．‎17cm D．‎16cm或‎17cm ‎【答案】D ‎8.‎ 二、填空题 ‎1. （2011山东滨州，15，4分）边长为‎6cm的等边三角形中，其一边上高的长度为________.‎ ‎【答案】cm ‎2. （2011山东烟台，14,4分）‎ 等腰三角形的周长为14，其一边长为4，那么，它的底边为 .‎ ‎【答案】4或6‎ ‎3. （2011浙江杭州，16，4）在等腰Rt△ABC中，∠C=90°，AC＝1，过点C作直线l∥AB，F是l上的一点，且AB＝AF，则点F到直线BC的距离为 ．‎ ‎【答案】‎ ‎4. （2011浙江台州，14,5分）已知等边△ABC中，点D,E分别在边AB,BC上，把△BDE沿直线DE翻折，使点B落在点Bˊ处，DBˊ,‎ EBˊ分别交边AC于点F，G，若∠ADF=80º ，则∠EGC的度数为 ‎ ‎【答案】80º ‎5. （2011浙江省嘉兴，14，5分）如图，在△ABC中，AB=AC，，则△ABC的外角∠BCD＝　 　°．‎ ‎（第14题）‎ ‎【答案】110‎ ‎6. （2011湖南邵阳，11，3分）如图（四）所示，在△ABC中，AB=AC，∠B=50°，则∠A=_______。‎ ‎【答案】80°。提示：∠A=180°-2×50°=80°。‎ ‎7. （2011山东济宁，15，3分）如图，等边三角形ABC中，D、E分别为AB、BC边上的两个动点，且总使AD=BE，AE与CD交于点F，AG⊥CD于点G，则 ．‎ 第15题 D ‎【答案】‎ ‎8. （2011湖南怀化，13，3分）如图6，在△ABC中，AB=AC，∠BAC的角平分线交BC边于点D，AB=5，BC=6，则AD=__________________.‎ ‎【答案】4‎ ‎9. （2011四川乐山16，3分）如图，已知∠AOB=，在射线OA、OB上分别取点OA=OB，连结AB，在BA、BB上分别取点A、B，使B B= B A，连结A B…按此规律上去，记∠A B B=，∠，…，∠‎ 则⑴= ； ⑵ = 。‎ ‎【答案】⑴ ⑵‎ ‎10．（2011湖南邵阳，11，3分）如图（四）所示，在△ABC中，AB=AC，∠B=50°，则∠‎ A=_______。‎ ‎【答案】80°。‎ ‎11. （2011贵州贵阳，15，4分）如图，已知等腰Rt△ABC的直角边长为1，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推直到第五个等腰Rt△AFG，则由这五个等腰直角三角形所构成的图形的面积为______．‎ ‎（第15题图）‎ ‎ 【答案】 ‎12. （2011广东茂名，14，3分）如图，已知△ABC是等边三角形，点B、C、D、E在同一直线上，且CG＝CD，DF＝DE，则∠E＝ 度．‎ ‎【答案】15 ‎ 三、解答题 ‎1. （2011广东东莞，21，9分）如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=EF=9，∠BAC＝∠DEF＝90°，固定△ABC，将△EFD绕点A 顺时针旋转，当DF边与AB边重合时，旋转中止.不考虑旋转开始和结束时重合的情况，设DE、DF（或它们的延长线）分别交BC（或它的延长线）于G、H点，如图（2）.‎ ‎（1）问：始终与△AGC相似的三角形有 及 ；‎ ‎（2）设CG＝x，BH＝y，求y关于x的函数关系式（只要求根据2的情况说明理由）；‎ ‎（3）问：当x为何值时，△AGH是等腰三角形？‎ ‎【解】（1）△HGA及△HAB；‎ ‎ （2）由（1）可知△AGC∽△HAB ‎∴，即，‎ 所以，‎ ‎（3）当CG＜时，∠GAC=∠H＜∠HAC，∴AC＜CH ‎∵AG＜AC，∴AG＜GH 又AH＞AG，AH＞GH 此时，△AGH不可能是等腰三角形；‎ 当CG=时，G为BC的中点，H与C重合，△AGH是等腰三角形；‎ 此时，GC=，即x=‎ 当CG＞时，由（1）可知△AGC∽△HGA 所以，若△AGH必是等腰三角形，只可能存在AG=AH 若AG=AH，则AC=CG，此时x=9‎ 综上，当x=9或时，△AGH是等腰三角形．‎ ‎2. （2011山东德州19,8分）如图 AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．‎ ‎（1）求证AD=AE；(2) 连接OA，BC，试判断直线OA，BC的关系并说明理由．‎ A B C E D O ‎【答案】A B E C D O （1）证明：在△ACD与△ABE中，‎ ‎∵∠A=∠A，∠ADC=∠AEB=90°，AB=AC，‎ ‎∴ △ACD≌△ABE．…………………… 3分 ‎∴ AD=AE． ……………………4分 ‎(2) 互相垂直 ……………………5分 在Rt△ADO与△AEO中，‎ ‎∵OA=OA，AD=AE，‎ ‎∴ △ADO≌△AEO． ……………………………………6分 ‎∴ ∠DAO=∠EAO．‎ 即OA是∠BAC的平分线． ………………………………………7分 ‎ 又∵AB=AC，‎ ‎∴ OA⊥BC． ………………………………………8分 ‎3. （2011山东日照，23，10分）如图，已知点D为等腰直角△ABC内一点，∠CAD＝∠CBD＝15°，E为AD延长线上的一点，且CE＝CA．‎ ‎（1）求证：DE平分∠BDC；‎ ‎（2）若点M在DE上，且DC=DM，‎ 求证： ME=BD．‎ ‎ 【答案】（1）在等腰直角△ABC中，‎ ‎∵∠CAD=∠CBD=15o，‎ ‎∴∠BAD=∠ABD=45o-15o=30o，‎ ‎∴BD=AD，∴△BDC≌△ADC， ‎ ‎∴∠DCA=∠DCB=45o．‎ 由∠BDM=∠ABD+∠BAD=30o+30o=60o，‎ ‎∠EDC=∠DAC+∠DCA=15o+45o=60o，‎ ‎∴∠BDM=∠EDC，‎ ‎∴DE平分∠BDC； ‎ ‎（2）如图，连接MC，‎ ‎∵DC=DM，且∠MDC=60°，‎ ‎∴△MDC是等边三角形，即CM=CD． ‎ 又∵∠EMC=180°-∠DMC=180°-60°=120°，‎ ‎∠ADC=180°-∠MDC=180°-60°=120°，‎ ‎∴∠EMC=∠ADC． ‎ 又∵CE=CA，‎ ‎∴∠DAC=∠CEM=15°，∴△ADC≌△EMC，∴ME=AD=DB． ‎ ‎4. （2011湖北鄂州，18，7分）如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长．‎ ‎ 第18题图 B A E D F C ‎【答案】连结BD，证△BED≌△CFD和△AED≌△BFD，求得EF=5‎ ‎5. （2011浙江衢州，23,10分）是一张等腰直角三角形纸板，.‎ 要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图1），比较甲、乙两种剪法，哪种剪法所得的正方形面积更大？请说明理由. ‎ ‎（第23题）‎ ‎（第23题图1）‎ 图1中甲种剪法称为第1次剪取，记所得的正方形面积为；按照甲种剪法，在余下的 中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为(如图2)，则 ；再在余下的四个三角形中，用同样的方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形的面积和为(如图3)；继续操作下去…则第10次剪取时， . ‎ 求第10次剪取后，余下的所有小三角形的面积和.‎ ‎【答案】(1)解法1：如图甲，由题意得.如图乙，设，则由题意，得 又 甲种剪法所得的正方形的面积更大 说明：图甲可另解为：由题意得点D、E、F分别为的中点，‎ 解法2：如图甲，由题意得 如图乙，设 甲种剪法所得的正方形的面积更大 ‎(2)‎ ‎(3)‎ ‎(3)解法1：探索规律可知：‘‎ 剩余三角形的面积和为：‎ 解法2：由题意可知，‎ 第一次剪取后剩余三角形面积和为 第二次剪取后剩余三角形面积和为 第三次剪取后剩余三角形面积和为 ‎…‎ 第十次剪取后剩余三角形面积和为 ‎6. (2011浙江绍兴，23，12分)数学课上，李老师出示了如下框中的题目.‎ 小敏与同桌小聪讨论后，进行了如下解答：‎ ‎（1）特殊情况，探索结论 当点为的中点时，如图1，确定线段与的大小关系，请你直接写出结论：‎ ‎ （填“>”,“<”或“=”）. ‎ 第25题图2‎ 第25题图1‎ ‎（2）特例启发，解答题目 解：题目中，与的大小关系是： （填“>”,“<”或“=”）.理由如下：如图2，过点作，交于点.‎ ‎（请你完成以下解答过程）‎ ‎（3）拓展结论，设计新题 在等边三角形中，点在直线上，点在直线上，且.若的边长为1，，求的长（请你直接写出结果）. ‎ ‎【答案】（1）= .‎ ‎（2）=.‎ 方法一：如图，等边三角形中，‎ 是等边三角形，‎ 又 ‎.‎ 方法二：在等边三角形中，‎ 而由是正三角形可得 ‎ ‎ ‎(3)1或3.‎ ‎7. （2011浙江台州，23,12分）如图1，过△ABC的顶点A分别做对边BC上的高AD和中线AE，点D是垂足，点E是BC中点，规定。特别的，当点D重合时，规定。另外。对、作类似的规定。‎ ‎（1）如图2，已知在Rt△ABC中，∠A=30º，求、；‎ ‎（2）在每个小正方形边长为1的4×4方格纸上，画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且，面积也为2；‎ ‎（3）判断下列三个命题的真假。（真命题打√，假命题打×）‎ ‎① 若△ABC中，，则△ABC为锐角三角形；（ ）‎ ‎② 若△ABC中，，则△ABC为直角三角形；（ ）‎ ‎③ 若△ABC中，，则△ABC为钝角三角形；（ ）‎ ‎【答案】解:（1）如图，作CD⊥AB，垂足为D，作中线CE、AF。‎ ‎ ‎ ‎ ∴=1‎ ‎ ∵ Rt△ABC中，∠CAB=30º， ∴ AE=CE=BE ,∠CEB=60º，‎ ‎ ∴△CEB是正三角形，‎ ‎∵ CD⊥AB ∴ AE=2DE ‎ ∴=； ∴=1，=；‎ ‎ （2）如图所示：‎ ‎ （3）①×；②√；③√。‎ ‎8. （2011浙江义乌，23，10分）如图1，在等边△ABC中，点D是边AC的中点，点P是线段DC上的动点(点P与点C不重合)，连结BP. 将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P,连结AA1，射线AA1分别交射线PB、射线B1B于点E、F.‎ ‎ （1） 如图1，当0°＜α＜60°时，在α角变化过程中，△BEF与△AEP始终存在 ▲ 关系（填“相似”或“全等”），并说明理由；‎ ‎（2）如图2，设∠ABP=β . 当60°＜α＜180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由； ‎ ‎（3）如图3，当α=60°时，点E、F与点B重合. 已知AB=4，设DP=x，△A1BB1的面 积为S，求S关于x的函数关系 图1‎ 图2‎ 图3‎ P B1‎ FM A DO EC C B A1‎ P B1‎ FM A DO EC C B A1‎ P B1‎ A DO C B A1‎ ‎【答案】（1） 相似 ‎ 由题意得：∠APA1=∠BPB1=α AP= A1P BP=B1P ‎ 则 ∠PAA1 =∠PBB1 = ‎ ‎ ∵∠PBB1 =∠EBF ∴∠PAE=∠EBF ‎ 又∵∠BEF=∠AEP ‎ ‎∴△BEF ∽△AEP ‎（2）存在，理由如下：‎ 易得：△BEF ∽△AEP 若要使得△BEF≌△AEP，只需要满足BE=AE即可 ‎∴∠BAE=∠ABE ‎ ∵∠BAC=60° ∴∠BAE=‎ ‎∵∠ABE=β ∠BAE=∠ABE ‎ ‎∴ 即α=2β+60° ‎ ‎（3）连结BD，交A1B1于点G，‎ 过点A1作A1H⊥AC于点H. ‎ P B1‎ A DO C B A1‎ H G ‎∵∠B‎1 A1P=∠A1PA=60° ∴A1B1∥AC ‎ 由题意得：AP= A1 P ∠A=60°‎ ‎ ∴△PAA1是等边三角形 ‎∴A1H=在Rt△ABD中，BD=‎ ‎ ∴BG=‎ ‎∴ （0≤x＜2）‎ ‎9. （2011广东株洲，20，6分）如图， △ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC．‎ ‎（1）求∠ECD的度数；‎ ‎（2）若CE=5，求BC长．‎ ‎【答案】（1）解法一：∵DE垂直平分AC，∴CE=AE，∠ECD=∠A=36°. ‎ 解法二：∵DE垂直平分AC，∴AD=CD，∠ADE=∠CDE=90°， ‎ 又∵DE =DE，∴△ADE≌△CDE，∠ECD=∠A=36°. ‎ ‎（2）解法一：∵AB=AC，∠A=36°，∴∠B=∠ACB=72°，‎ ‎∵∠ECD=36°，‎ ‎∴∠BCE=∠ACB-∠ECD=36°，‎ ‎∠BEC=72°=∠B，‎ ‎∴ BC=EC=5.‎ 解法二：∵AB=AC，∠A=36°，‎ ‎∴∠B=∠ACB=72°， ‎ ‎∴∠BEC=∠A+∠ECD=72°， ‎ ‎∴∠BEC=∠B，‎ ‎∴BC=EC=5. ‎ ‎10．(2011重庆綦江，24，10分)如图，等边△ABC中，AO是∠BAC的角平分线，D为AO上一点，以CD为一边且在CD下方作等边△CDE,连结BE. ‎ ‎ (1) 求证：△ACD≌△BCE； ‎ ‎ (2) 延长BE至Q, P为BQ上一点，连结CP、CQ使CP＝CQ＝5, 若BC＝8时，求PQ的长.‎ ‎ ‎ ‎【答案】：(1)证明ABC和△CDE均为等边三角形，‎ ‎ ∴AC＝BC , CD＝CE ‎ ‎ 且∠ACB＝∠DCE＝60°‎ ‎ ∵∠ACD＋∠DCB＝∠DCB＋∠BCE＝60°‎ ‎ ∴∠ACD＝∠BCE ‎ ‎ ∴△ACD≌△BCE ‎ ‎（2）解：作CH⊥BQ交BQ于H, 则PQ＝2HQ ‎ ‎ 在Rt△BHC中 ，由已知和（1）得∠CBH＝∠CAO＝30°，∴ CH＝4 ‎ 在Rt△CHQ中，HQ＝ ‎ ‎ ∴PQ＝2HQ＝6 ‎ ‎11. （2011江苏扬州，23,10分）已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC，‎ ‎（1）求证：△ABC是等腰三角形；‎ ‎（2）判断点O是否在∠BAC的角平分线上，并说明理由。‎ ‎【答案】（1）证明：∵OB=OC ∴∠OBC=∠OCB ‎∵BD、CE是两条高 ∴∠BDC=∠CEB=90°‎ 又∵BC=CB ∴△BDC≌△CEB（AAS）‎ ‎∴∠DBC=∠ECB ∴AB=AC ‎ ‎∴△ABC是等腰三角形。‎ ‎ （2）点O是在∠BAC的角平分线上。连结AO. ‎ ‎∵ △BDC≌△CEB ∴DC=EB,‎ ‎∵OB=OC ∴ OD=OE 又∵∠BDC=∠CEB=90° AO=AO ‎ ‎∴△ADO≌△AEO（HL） ‎ ‎∴∠DAO=∠EAO ‎ ‎∴点O是在∠BAC的角平分线上。‎ ‎12. （2011广东省，21，9分）如图（1），△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=EF=9，∠BAC＝∠DEF＝90°，固定△ABC，将△EFD绕点A 顺时针旋转，当DF边与AB边重合时，旋转中止.不考虑旋转开始和结束时重合的情况，设DE、DF（或它们的延长线）分别交BC（或它的延长线）于G、H点，如图（2）.‎ ‎（1）问：始终与△AGC相似的三角形有 及 ；‎ ‎（2）设CG＝x，BH＝y，求y关于x的函数关系式（只要求根据2的情况说明理由）；‎ ‎（3）问：当x为何值时，△AGH是等腰三角形？‎ ‎【解】（1）△HGA及△HAB；‎ ‎ （2）由（1）可知△AGC∽△HAB ‎∴，即，‎ 所以，‎ ‎（3）当CG＜时，∠GAC=∠H＜∠HAC，∴AC＜CH ‎∵AG＜AC，∴AG＜GH 又AH＞AG，AH＞GH 此时，△AGH不可能是等腰三角形；‎ 当CG=时，G为BC的中点，H与C重合，△AGH是等腰三角形；‎ 此时，GC=，即x=‎ 当CG＞时，由（1）可知△AGC∽△HGA 所以，若△AGH必是等腰三角形，只可能存在AG=AH 若AG=AH，则AC=CG，此时x=9‎ 综上，当x=9或时，△AGH是等腰三角形．‎ ‎13. （2011湖北黄冈，18，7分）如图，在等腰三角形ABC中，∠ABC=90°‎ ‎，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长．‎ ‎ 第18题图 B A E D F C ‎【答案】连结BD，证△BED≌△CFD和△AED≌△BFD，求得EF=5‎ ‎14. （2011湖北襄阳，21，6分）‎ 如图6，点D，E在△ABC的边BC上，连接AD，AE. ①AB＝AC；②AD＝AE；③BD＝CE.以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②③；①③②；②③①.‎ ‎（1）以上三个命题是真命题的为（直接作答） ；‎ ‎（2）请选择一个真命题进行证明（先写出所选命题，然后证明）.‎ 图6‎ ‎【答案】（1）①②③；①③②；②③①. 3分 ‎（2）（略） 6分 ‎15. （2011山东泰安，29 ，10分）已知：在△ABC中，AC=BC，∠ACB=900，点D是AB的中点，点E是AB边上一点。‎ ‎（1）直线BF垂直于CE于点F，交CD于点G（如图①），求证：AE=CG；‎ ‎（2）直线AH垂直于CE于，垂足为H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并说明。‎ ‎【答案】（1）证明：∵点D是AB中点，AC=BC，∠ACB=900‎ ‎ ∴CD⊥AB，∠ACD=∠BCD=450‎ ‎∠CAD=∠CBD=450‎ ‎∴∠CAE=∠BCG 又BF⊥CE ‎∴∠CBG+∠BCG=900‎ 又∠ACE+∠BCF=900‎ ‎∴∠ACE=∠CBG ‎∴△AEC≌△CGB ‎∴AE=CG ‎（2）BE=CM 证明：∵CH⊥HM，CD⊥ED ‎∴∠CMA+∠MCH=900‎ ‎∠BEC+∠MCH=900‎ ‎∴∠CMA=∠BEC 又，AC=BC，∠ACM=∠CBE=450‎ ‎∴△BCE≌△CAM ‎∴BE=CM 一、选择题 ‎1．（2010浙江宁波） 如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是△ABC、△BCD的角平分线，‎ ‎ 则图中的等腰三角形有 ‎ (A)5个 (B)4个 (C)3个 (D)2个 ‎(第10题)‎ ‎【答案】A ‎ ‎2．（2010 浙江义乌）如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA=5，则线段PB的长度为（ ▲ ）‎ A B C D P A．6 B．‎5 C．4 D．3‎ ‎【答案】B ‎3．（2010江苏无锡）下列性质中，等腰三角形具有而直角三角形不一定具有的是 （ ）‎ A．两边之和大于第三边 B．有一个角的平分线垂直于这个角的对边 C．有两个锐角的和等于90° D．内角和等于180°‎ ‎【答案】B ‎ ‎4.（2010 黄冈）如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为（　　　）‎ A．　　B．　　C．　　D．不能确定 ‎　　　　　第15题图 ‎【答案】B．‎ ‎5．（2010山东烟台）如图，等腰△ ABC中，AB=AC，∠A=20°。线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于 A、80° B、 70° C、60° D、50°‎ ‎【答案】C ‎ ‎6．（2010江西）已知等腰三角形的两条边长分别是7和3，则下列四个数中，第三条边的长是( )‎ A．8 B．‎7 C． 4 D．3‎ ‎【答案】B ‎7．（2010湖北武汉）如图，△ABC内有一点D，且DA=DB=DC，若∠DAB=20°，∠DAC=30°，则∠BDC的大小是（ ）‎ A.100° B.80°‎ C.70° D.50°‎ ‎【答案】A ‎8．（2010山东威海）如图，在△ABC中，D，E分别是边AC，AB的中点， ‎ 连接BD．若BD平分∠ABC，则下列结论错误的是 ‎ A D B E A．BC＝2BE ‎ B．∠A＝∠EDA ‎ C C．BC＝2AD ‎ D．BD⊥AC ‎ ‎【答案】C ‎ ‎9．（2010 湖南株洲）如图所示的正方形网格中，网格线的交点称为格点．已知、‎ 是两格点，如果也是图中的格点，且使得为等腰三角形，则点的个数是 第8题图 A．6 B．‎7 ‎C．8 D．9‎ ‎【答案】C ‎ ‎10．（2010云南楚雄）已知等腰三角形的一个内角为70°，则另外两个内角的度数是（ ）‎ A．55°，55° B．70°，40° C．55°，55°或70°，40° D．以上都不对 ‎【答案】C ‎11．（2010湖北随州）如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为（　　　）‎ A．　　B．　　C．　　D．不能确定 ‎　　　　　第15题图 ‎【答案】B ‎ ‎12．（2010湖北襄樊）已知：一等腰三角形的两边长x、y满足方程组则此等腰三角形的周长为（ ）‎ A．5 B．‎4 ‎ C．3 D．5或4‎ ‎ ‎ ‎【答案】A ‎ ‎13．（2010 山东东营）如图，点C是线段AB上的一个动点，△ACD和△BCE是在AB同侧的两个等边三角形，DM，EN分别是△ACD和△BCE的高，点C在线段AB上沿着从点A向点B的方向移动(不与点A，B重合)，连接DE，得到四边形DMNE．这个四边形的面积变化情况为（ ）‎ ‎（A）逐渐增大 (B) 逐渐减小 (C) 始终不变 (D) 先增大后变小 ‎【答案】C ‎ ‎14．（2010 广东汕头）如图，把等腰直角△ABC沿BD折叠，使点A落在边BC 上的点E处．下面结论错误的是（　　）‎ A．AB＝BE B．AD＝DC　 C．AD＝DE　 D．AD＝EC ‎【答案】B ‎ ‎15．（2010 重庆江津）已知：△ABC中，AB=AC=，BC=6，则腰长的 取值范围是（ ）‎ A． B． ‎ ‎ C． D．‎ ‎【答案】B ‎ ‎16．（2010 重庆江津）如图，在Rt△ABC 中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△绕点顺时针旋转90后，得到△，连接．下列结论中正确的个数有（ ）‎ ‎① ②△∽△‎ ‎③平分 ④‎ A．１个　 B．２个　 C．３个　　 D．４个　　　　　　　　‎ ‎【答案】C ‎ ‎17．（2010广东茂名）如图，吴伯伯家有一块等边三角形的空地ABC，已知点E、F分别是边AB、AC的中点，量得EF＝‎5米，他想把四边形BCFE用篱笆围成一圈放养小鸡，则需用篱笆的长是 ‎(第5题图)‎ A、15米 B、‎20米 C、‎25米 D、‎‎30米 ‎【答案】C ‎ ‎18．（2010广东深圳）如图1，△ABC中，AC=AD=BD，∠DAC=80°。则∠B的度数是 A．40° B．35° C．25° D．20°‎ ‎【答案】C ‎ ‎19．（2010贵州铜仁）如图，小红作出了边长为1的第1个正△A1B‎1C1，算出了正△A1B‎1C1的面积，然后分别取△A1B‎1C1三边的中点A2，B2，C2，作出了第2个正△A2B‎2C2，算出了正△A2B‎2C2的面积，用同样的方法，作出了第3个正△A3B‎3C3，算出了正△A3B‎3C3的面积……，由此可得，第8个正△A8B‎8C8的面积是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎ ‎20．（2010四川广安）等腰三角形的两边长为4、9，则它的周长是 ‎ A．17 B．17或‎22 C．20 D．22‎ ‎【答案】D ‎ ‎21．（2010黑龙江绥化）如图所示，已知△ABC和△DCE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F，连结OC、FG，则下列结论：①AE＝BD ②AG＝BF ③FG∥BE ④∠BOC＝∠EOC，其中正确结论的个数（ ）‎ A.1个 B.2个 C.3个 D.4个 ‎【答案】D ‎ ‎22．（2010广东清远）等腰三角形的底角为40°，则这个等腰三角形的顶角为( )‎ A．40° B．80° C．100° D．100°或40°‎ ‎【答案】C ‎ 二、填空题 ‎1．如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC是等腰三角形的是__________________。（把所有正确答案的序号都填写在横线上）‎ ‎①∠BAD＝∠ACD ②∠BAD＝∠CAD，‎ ‎③AB+BD＝AC+CD ④AB-BD＝AC-CD ‎【答案】﹝2﹞﹝3﹞﹝4﹞‎ ‎2．（2010广东广州，16，3分）如图4，BD是△ABC的角平分线，∠ABD＝36°，∠C＝72°，则图中的等腰三角形有_____个．‎ ‎【答案】3‎ ‎3．（2010江苏无锡）如图，△ABC中，DE垂直平分AC交AB于E，∠A=30°，‎ ‎∠ACB=80°，则∠BCE= ▲ °．‎ ‎（第16题）‎ ‎【答案】50° ‎ ‎4．（2010江苏泰州）等腰△ABC的两边长分别为2和5，则第三边长为 ．‎ ‎【答案】5‎ ‎5．（2010四川眉山）如图，将第一个图（图①）所示的正三角形连结各边中点进行分割，得到第二个图（图②）；再将第二个图中最中间的小正三角形按同样的方式进行分割，得到第三个图（图③）；再将第三个图中最中间的小正三角形按同样的方式进行分割，……，则得到的第五个图中，共有________个正三角形．‎ ‎……‎ ‎【答案】17‎ ‎6．（2010浙江绍兴）做如下操作：在等腰三角形ABC中,AB= AC,AD平分∠BAC,‎ 交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的 像与△ACD重合.‎ 第15题图 对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三角形的顶角平分线、底边上的中线 和高互相重合.‎ 由上述操作可得出的是 (将正确结论的序号都填上). ‎ ‎【答案】②③‎ ‎7．（2010江苏淮安）已知周长为8的等腰三角形，有一个腰长为3，则最短的一条串位线长为 ．‎ ‎【答案】1.5‎ ‎8．（2010 山东滨州）如图,等边△‎ ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为 . ‎ ‎【答案】‎ ‎9．（2010四川内江）下面的方格图案中的正方形顶点叫做格点，图1中以格点为顶点的等腰直角三角形有4个，图2中以格点为顶点的等腰直角三角形有　　　　　个，图3中以格点为顶点的等腰直角三角形有　　　　　个，图4中以格点为顶点的等腰直角三角形有　　　　　个.‎ 图2‎ 图1‎ 图4‎ 图3‎ ‎【答案】10，28，50　‎ ‎10．（2010 湖南湘潭）△ABC中，若∠A=80o， ∠B=50o，AC=5，则AB= .‎ ‎【答案】5‎ ‎11．（2010广西桂林）如图：已知AB=10，点C、D在线段AB上且AC=DB=2； P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连结EF，设EF的中点为G；当点P从点C运动到点D时，则点G移动路径的长是________．‎ ‎【答案】3‎ ‎12．（2010 广西钦州市）如图，△ABC是一个边长为2的等边三角形，AD0⊥BC，垂足为点D0．过点D0作D0D1⊥AB，垂足为点D1；再过点D1作D1D2⊥AD0，垂足为点D2；又过点D2作D2D3⊥AB，垂足为点D3；……；这样一直作下去，得到一组线段：D0D1，D1D2，D2D3，……，则线段Dn-1Dn的长为_ ▲ _（n为正整数）． ‎ 第10题 D1‎ D5‎ D2‎ D3‎ D4‎ D0‎ ‎ 全品中考网 ‎【答案】‎ ‎13．（2010年山西）如图，在△ABC中，AB=AC=13，BC=10，D是AB的中点，过点D作DE⊥AC于点E，则DE的长是 。‎ ‎【答案】‎ ‎14．（2010天门、潜江、仙桃）从一个等腰三角形纸片的底角顶点出发，能将其剪成两个等腰三角形纸片，则原等腰三角形纸片的底角等于 .‎ ‎【答案】72°，（）°‎ ‎15．（2010四川攀枝花）如图8，在△ABC中，AB=AC=2，∠BAC=90,‎ 直角∠EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F．给出以下四个结论：‎ ‎①BE=AF,②Ｓ△EPF的最小值为,③tan∠PEF=，④Ｓ四边形AEPF=１.当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），上述结论始终正确是 ．（将正确的命题序号全部写上）‎ C A 图8‎ P E F B ‎【答案】①②④‎ ‎16．（2010湖北黄石） 如图，等腰三角形ABC中，已知AB＝AC，∠A＝30°，AB的垂直平分线交AC于D，则∠CBD的度数为 .‎ ‎【答案】‎ 三、解答题 ‎1．（2010辽宁丹东市）如图， 已知等边三角形ABC中，点D，E，F分别为边AB，AC，BC的中点，M为直线BC上一动点，△DMN为等边三角形（点M的位置改变时， △DMN也随之整体移动） ．‎ ‎ （1）如图①，当点M在点B左侧时，请你判断EN与MF有怎样的数量关系？点F是否在直线NE上？都请直接写出结论，不必证明或说明理由；‎ ‎ （2）如图②，当点M在BC上时，其它条件不变，（1）的结论中EN与MF的数量关系是否仍然成立?若成立，请利用图②证明；若不成立，请说明理由；‎ ‎（3）若点M在点C右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论，不必证明或说明理由． ‎ 图①‎ 图②‎ 图③‎ 第25题图 A ‎·‎ B C D E F ‎·‎ ‎·‎ ‎·‎ ‎【答案】（1）判断：EN与MF相等 （或EN=MF），点F在直线NE上， 3分 ‎（说明：答对一个给2分）‎ ‎（2）成立． 4分 证明：‎ 法一：连结DE，DF． 5分 ‎∵△ABC是等边三角形， ∴AB=AC=BC．‎ 又∵D，E，F是三边的中点， ‎ ‎∴DE，DF，EF为三角形的中位线．∴DE=DF=EF，∠FDE=60°．‎ 又∠MDF+∠FDN=60°， ∠NDE+∠FDN=60°， ‎ ‎∴∠MDF=∠NDE． 7分 在△DMF和△DNE中，DF=DE，DM=DN， ∠MDF=∠NDE，‎ ‎∴△DMF≌△DNE． 8分 N C A B F M D E N C A B F M D E ‎∴MF=NE． 　 9分 法二：‎ 延长EN，则EN过点F． 5分 ‎∵△ABC是等边三角形， ∴AB=AC=BC．‎ 又∵D，E，F是三边的中点， ∴EF=DF=BF． ‎ ‎ ∵∠BDM+∠MDF=60°， ∠FDN+∠MDF=60°，‎ ‎∴∠BDM=∠FDN． 7分 又∵DM=DN， ∠ABM=∠DFN=60°，‎ ‎∴△DBM≌△DFN． 8分 ‎∴BM=FN．‎ ‎∵BF=EF， ∴MF=EN． 9分 法三：‎ 连结DF，NF． 5分 ‎∵△ABC是等边三角形， ‎ ‎∴AC=BC=AC．‎ 又∵D，E，F是三边的中点， ‎ ‎∴DF为三角形的中位线，∴DF=AC=AB=DB． ‎ 又∠BDM+∠MDF=60°， ∠NDF+∠MDF=60°， ‎ ‎∴∠BDM=∠FDN． 7分 在△DBM和△DFN中，DF=DB，‎ DM=DN， ∠BDM=∠NDF，∴△DBM≌△DFN． ‎ ‎∴∠B=∠DFN=60°． 8分 又∵△DEF是△ABC各边中点所构成的三角形，‎ ‎∴∠DFE=60°．‎ ‎∴可得点N在EF上，‎ ‎∴MF=EN． 9分 ‎（3）画出图形（连出线段NE）， 11分 MF与EN相等的结论仍然成立（或MF=NE成立）． 12分 ‎2．（2010 福建晋江）（13分）如图，在等边中，线段为边上的中线. 动点在直线上时，以为一边且在的下方作等边，连结.‎ ‎(1) 填空：度；‎ ‎(2) 当点在线段上(点不运动到点)时，试求出的值；‎ ‎(3)若，以点为圆心，以5为半径作⊙与直线相交于点、两点，在点运动的过程中(点与点重合除外)，试求的长.‎ A B C 备用图(1)‎ A B C 备用图(2)‎ ‎【答案】26.（本小题13分）‎ ‎(1)60；…………………………………………（3分）‎ ‎(2)∵与都是等边三角形 ‎∴，，‎ ‎∴‎ ‎∴……………………………（5分）‎ ‎∴≌‎ ‎∴，∴.………………………（7分）‎ ‎(3)①当点在线段上（不与点重合）时，由(2)可知≌，则，作于点，则，连结，则.‎ 在中，，，则.‎ 在中，由勾股定理得：，则.………………………（9分）‎ ‎②当点在线段的延长线上时，∵与都是等边三角形 ‎∴，，‎ ‎∴‎ ‎∴‎ ‎∴≌‎ ‎∴，同理可得：.…………………………（11分）‎ ‎③当点在线段的延长线上时，‎ ‎∵与都是等边三角形 ‎∴，，‎ ‎∴‎ ‎∴‎ ‎∴≌‎ ‎∴‎ ‎∵‎ ‎∴‎ ‎∴.‎ 同理可得：.‎ 综上，的长是6. ………………………（13分）‎ ‎3．（2010 山东济南）（1）如图，已知．求证．‎ A C E D B ‎【答案】证明：∵AB=AC ‎∴∠B=∠C ∵AD=AE ‎∴∠ADE=∠AEC ‎∴180O -∠ADE=180O -∠AEC ‎ 即∠ADB=∠AEC ‎ 在△ABD和△ACE中 ‎∵AB=AC ‎∠B=∠C ‎∠ADB=∠AEC ‎∴△ABD≌△ACE ‎ ‎∴BD=CE ‎ ‎4．（2010湖南衡阳）已知：如图，在等边三角形ABC的AC边上取中点D，BC的延长线上取一点E，使 CE ＝ CD．求证：BD ＝ DE．‎ ‎、【答案】∵△ABC是等边三角形，∴∠ABC=∠ACB=60°，∵D为AC中点，∴∠DBC=30°，∵CE ＝ CD，∴∠E=30°，∴∠DBC=∠E，∴BD ＝ DE.‎ ‎5．（2010 山东省德州）如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．‎ ‎(1)求证：AB＝DC；‎ ‎(2)试判断△OEF的形状，并说明理由．‎ A D B E F C O 第18题图 A D B E F C O ‎【答案】证明：（１）∵BE＝CF，‎ ‎∴BE＋EF＝CF＋EF， ‎ 即BF＝CE． ‎ 又∵∠A＝∠D，∠B＝∠C，‎ ‎∴△ABF≌△DCE（AAS）， ‎ ‎∴AB＝DC． ‎ ‎（２）△OEF为等腰三角形 ‎ 理由如下：∵△ABF≌△DCE，‎ ‎∴∠AFB=∠DEC．‎ ‎∴OE=OF．‎ ‎∴△OEF为等腰三角形． ‎ ‎6．（2010江苏常州）如图，在△ABC中，点D、E分别在边AC、AB上，BD=CE，‎ ‎∠DBC=∠ECB。‎ 求证：AB=AC。‎ ‎【答案】‎ ‎7．（2010四川内江）如图，△ACD和△BCE都是等腰直角三角形，∠ACD＝∠BCE＝90°，AE交DC于F，BD分别交CE，AE于点G、H.‎ 试猜测线段AE和BD的位置和数量关系，并说明理由. ‎ F G H ‎ ‎ ‎【答案】解：猜测 AE＝BD，AE⊥BD. 2分 ‎ 理由如下：‎ ‎∵∠ACD＝∠BCE＝90°，‎ ‎∴∠ACD＋∠DCE＝∠BCE＋∠DCE，即∠ACE＝∠DCB. 3分 ‎∵△ACD和△BCE都是等腰直角三角形，‎ ‎∴AC＝CD，CE＝CB. 4分 ‎∴△ACE≌△DCB（S.A.S.） 5分 ‎∴AE＝BD， 6分 ‎∠CAE＝∠CDB,. 7分 ‎∵∠AFC＝∠DFH，‎ ‎∴∠DHF＝∠ACD＝90°， 8分 ‎∴AE⊥BD. 9分 ‎ ‎8．（2010 福建三明）如图，都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点。 全品中考网 ‎ （1）求证：△ACE≌△BCD；（5分）‎ ‎ （2）若AD=5，BD=12，求DE的长。（5分）‎ ‎【答案】（1）证明：都是等腰直角三角形 ‎∴AC=BC，EC=DC …………2分 ‎ …………3分 在中，AC=BC EC=DC ‎ ‎≌ …………3分 ‎ （2）解：由（1）可得AE=BD，‎ 又 ‎，即是直角三角形…………8分 ‎ …………10分 ‎9．（2010湖北襄樊） 如图5，点E、C在BF上，BF=FC，∠ABC=∠DEF=45°，∠A=∠D=90°．‎ ‎ （1）求证：AB=DE；‎ ‎ （2）若AC交DE于M，且AB=，ME=，将线段CE绕点C顺时针旋转，使点E旋转到AB上的G处，求旋转角∠ECG的度数．‎ 图5‎ ‎ ‎ ‎【答案】（1）∵BE=FC，∴BC=EF．‎ 又∵∠ABC=∠DEF，∠A=∠D，‎ ‎∴△ABC≌△DEF．‎ ‎∴AB=DE．‎ ‎（2）∵∠DEF=∠B=45°，∴DE//AB．∴∠CME=∠A=90°．‎ ‎∴AC=AB=，MC=ME=．‎ ‎∴CG=CE=2．‎ 在Rt△CAG中，cos∠ACG=，∴∠ACG=30°．‎ ‎∴∠ECG=∠ACB－∠ACG=45°－30°=15°．‎ ‎10．（2010 内蒙古包头）如图，已知中，厘米，厘米，点为的中点．‎ ‎（1）如果点P在线段BC上以‎3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．‎ ‎①若点Q的运动速度与点P的运动速度相等，经过1秒后，与是否全等，请说明理由；‎ ‎②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使与全等？‎ ‎（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿三边运动，求经过多长时间点P与点Q第一次在的哪条边上相遇？‎ A Q C D B P ‎【答案】A Q C D B P 解：（1）①∵秒，‎ ‎∴厘米，‎ ‎∵厘米，点为的中点，‎ ‎∴厘米．‎ 又∵厘米，‎ ‎∴厘米，‎ ‎∴．‎ 又∵，‎ ‎∴，‎ ‎∴． （4分）‎ ‎②∵， ∴，‎ 又∵，，则，‎ ‎∴点，点运动的时间秒，‎ ‎∴厘米/秒． （7分）‎ ‎（2）设经过秒后点与点第一次相遇，‎ 由题意，得，‎ 解得秒．‎ ‎∴点共运动了厘米．‎ ‎∵，‎ ‎∴点、点在边上相遇，‎ ‎∴经过秒点与点第一次在边上相遇． （12分）‎ ‎11．（2010湖北十堰）如图，△ABC中，AB=AC，BD⊥AC，‎ CE⊥AB.‎ 求证：BD=CE.‎ A B C D E ‎（第19题）‎ ‎【答案】证明：∵BD⊥AC，CE⊥AB ‎ ∴∠ADB=∠AEC=90°‎ 在△ABD和△AEC中，∠ADB=∠AEC=90°，∠A=∠A，AB=AC ‎∴△ABD≌△AEC ‎∴BD=CE.‎ ‎12．（2010广东深圳）如图8，△AOB和△COD均为等腰直角三角形，∠AOB=∠COD=90°，D在AB上。‎ ‎（1）求证：△AOC≌△BOD；（4分）‎ ‎（2）若AD=1，BD=2，求CD的长。（3分）‎ ‎【答案】（1）证明：如右图，‎ 图8‎ ‎，‎ 又，‎ ‎（2）由有：，，‎ ‎，故 ‎2009年中考试题专题之17-等腰三角形与勾股定理试题及答案 一、选择题 ‎1．（2009年山西省）如图，在RtΔABC中，∠ACB＝90°BC＝3,AC＝4,AB的垂直平分线DE交BC的延长线于点E，则CE的长为（ ）‎ A． B． C． D．2‎ A D B E C ‎【关键词】相似三角形判定和性质；勾股定理；线段和角的概念、性质 ‎【答案】B ‎2．(2009年达州)图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是 A．13 B．‎26 ‎‎ ‎‎ C．47 D．94 ‎ ‎【关键词】勾股定理 ‎【答案】C ‎3．（2009年湖北十堰市）如图，已知RtΔABC中，∠ACB＝90°，AC＝ 4，BC＝3，以AB边所在的直线为轴，将ΔABC旋转一周，则所得几何体的表面积是（ ）．‎ A． B． C． D．‎ ‎4．(2009年湖州)如图，在正三角形中，D，E，F分别是BC，AC，AB上的点，DE⊥AC,EF⊥AB,FD⊥BC，则ΔDEF的面积与ΔABC的面积之比等于（ ）‎ A．1∶3 B．2∶‎3 ‎ C．∶2 D．∶3 ‎ D C E F A B ‎【关键词】等边三角形的性质，相似的性质 ‎【答案】A ‎5．（2009年广西钦州）如图，AC＝AD，BC＝BD，则有（ ）‎ ‎ A．AB垂直平分CD B．CD垂直平分AB ‎ C．AB与CD互相垂直平分 D．CD平分∠ACB ‎【关键词】全等三角形、等腰三角形三线合一．‎ ‎【答案】A ‎6．（2009年衡阳市）如图2所示，A、B、C分别表示三个村庄，AB＝‎1000米，BC＝‎600米，AC＝‎800米，在社会主义新农村建设中，为了丰富群众生活，拟建一个 文化活动中心，要求这三个村庄到活动中心的距离相等，则活动中心P 的位置应在（ ）‎ A．AB中点 B．BC中点 C．AC中点 D．∠C的平分线与AB的交点 ‎【关键词】勾股定理的逆定理，三角形中垂线 ‎【答案】A ‎7．（湖北省恩施市）如图3，长方体的长为15，宽为10，高为20，点B离点C的距离为5，上只蚂蚁如果要沿着长方体的表面从点A爬到点B，需要爬行的最短距离是( )‎ A．5 B．‎25 C．+5 D．35‎ ‎8．（浙江省丽江市）如图，已知△ABC中，∠ABC＝90°,AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2 , l2，l3之间的距离为3 ,则AC的长是（ A ）‎ A． B． C． D．7‎ l1‎ l2‎ l3‎ A C B ‎∴ ．‎ ‎9．（2009白银市）如图，⊙O的弦AB＝6，M是AB上任意一点，且OM最小值为4，‎ 则⊙O的半径为（　　） ‎ A．5 B．‎4 C．3 D．2 ‎ ‎【关键词】勾股定理 ‎【答案】A ‎10．（2009年济宁市）“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．如图，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4．小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上）, 则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是 A． B． C． D． ‎ ‎【关键词】勾股定理 ‎【答案】C ‎ ‎ ‎11．（2009白银市）如图，四边形ABCD中，AB＝BC，∠ABC＝∠CDA＝90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE＝（　　）‎ A．2 B．‎3 ‎ C． D．‎ ‎【关键词】勾股定理，四边形的性质 ‎【答案】C ‎13．（2009年烟台市）如图，等边△ABC的边长为3，P为BC上一点，‎ 且BP＝1，D为AC上一点，若∠APD＝60°，则 CD的长为（ ）‎ A． B． C． D．‎ A D C P B ‎60°‎ ‎【关键词】等腰三角形 ‎【答案】B ‎13． （2009年嘉兴市）如图，等腰△ABC中，底边，ÐA＝36°，ÐABC的平分线交AC于D，ÐBCD的平分线交BD于E，设，则DE＝（　▲　）‎ A． B．‎ C． D．‎ A D C E B ‎【关键词】等腰三角形 ‎【答案】A ‎14．（2009泰安）如图，△ABC中，D、E分别是BC、AC的中点，BF平分∠ABC，交DE于点F，若BC＝6，则DF的长是 ‎（A）2 （B）3 （C） （D）4‎ ‎【关键词】角平分线、中位线 ‎【答案】B ‎15．（2009恩施市）如图，长方体的长为15，宽为10，高为20，点离点的距离为5，一只蚂蚁如果要沿着长方体的表面从点爬到点，需要爬行的最短距离是（　　　）‎ A． B．‎25 C． D．‎ ‎【关键词】图形的展开、勾股定理 ‎【答案】B ‎5‎ ‎20‎ ‎15‎ ‎10‎ C A B ‎16．（2009恩施市）16．如图6，的直径垂直弦CD于P，且P是半径OB的中点，CD＝‎6cm，则直径AB的长是（　　　）‎ A． B．‎ C． D．‎ ‎【关键词】垂径定理、勾股定理 ‎【答案】D ‎17．（2009丽水市）如图，已知△ABC中，∠ABC＝90°,AB＝BC，三角形的顶点在相互平行的三条直线l1，l2，l3上，且l1，l2之间的距离为2 , l2，l3之间的距离为3 ,则AC的长是（ ）‎ ‎ A． B． C． D．7‎ l1‎ l2‎ l3‎ A C B ‎【关键词】直线与直线的距离、勾股定理，解直角三角形 ‎【答案】A ‎18．．（2009年宁波市）等腰直角三角形的一个底角的度数是（ ）‎ A．30° B．45° C．60° D．90°‎ ‎【关键词】等腰三角形 ‎【答案】B ‎19． （2009年滨州）如图3，已知△ABC中，AB＝17，AC＝10，BC边上的高 AD＝8， 则边BC的长为（ ）‎ A．21 B．‎15 ‎ C．6 D．以上答案都不对 ‎【关键词】勾股定理．‎ ‎【答案】A A C D B ‎20．(2009武汉)9．如图，已知O是四边形ABCD内一点，OA＝OB＝OC，∠ABC＝∠ADC＝70°，则∠ADO+∠DCO的大小是（ ）‎ A．70° B．110° C．140° D．150°‎ B C O A D ‎【关键词】等腰三角形 多边形的内角和 ‎【答案】D 提示：∠BAO+∠BCO＝∠ABO+∠CBO＝∠ABC＝70°，所以∠BOA+∠BOC＝360°－140°＝220°，所以∠AOC＝140°。‎ ‎21．（2009重庆綦江）如图，点A的坐标是(2,2)，若点P在x轴上，且△APO是等腰三角形，则点P的坐标不可能是（ ）‎ A．(4，0) B．（1．0） y C．（-2，0） D．（2，0）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎-1‎ ‎1‎ ‎2‎ x y A ‎0‎ ‎【关键词】直角坐标系，等腰三角形 ‎【答案】B ‎22．（2009威海）如图，AB＝AC,BD＝BC，若∠A＝40°，则∠ABD的度数是（　　）‎ A． B． C． D．‎ B A D C ‎【关键词】等腰三角形 ‎【答案】B ‎ ‎ ‎23．（2009襄樊市）如图，已知直线且则等于（ B ）‎ A． 　　B．　　C． D．‎ A F B C D E 解析：本题考查平行线的性质、等腰三角形的性质等知识，∵所以，∴，∵∴，∴，故选B。‎ ‎【关键词】平行线的性质、等腰三角形的性质、三角形内角和定理 ‎【答案】B ‎24．（2009年贵州黔东南州）如图，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠A等于（ ）‎ A．30o B．40o C．45o D．36o ‎ ‎【关键词】等腰三角形 ‎【答案】D ‎25．(2009年温州)如图，△ABC中，AB＝AC＝6，BC＝8，AE平分么BAC交BC于点E，点D为AB的中点，连结DE，则△BDE的周长是( )‎ ‎ A．7+ B．‎10 C．4+2 D．12‎ ‎【关键词】等腰三角形“三线合一”的性质 ‎【答案】B ‎26．(2009年温州)一张等腰三角形纸片，底边长l‎5cm，底边上的高长22．‎5cm．现沿底边依次从下往上裁剪宽度均为‎3cm 的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是( )‎ A．第4张 B．第5张 C．第6张 D．第7张 ‎【关键词】等腰三角形性质，三角形相似的性质，梯形中位线 ‎【答案】C ‎27．(2009年云南省)如图，等腰△ABC的周长为21，底边BC ＝ 5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（ ）‎ A．13 B．14‎ C．15 D．16‎ A D E B C ‎【关键词】垂直平分线 等腰三角形 ‎【答案】A ‎（2009呼和浩特）在等腰中，，一边上的中线将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（ ）‎ A．7 B．‎11 ‎ C．7或11 D．7或10‎ ‎【关键词】等腰三角形 ‎【答案】‎ 二、填空题 ‎1． （2009年重庆市江津区）等腰三角形一腰上的高与另一腰的夹角为30º，腰长为‎4 cm，则其腰上的高为 ‎ cm．‎ ‎【关键词】等腰三角形的性质 ‎【答案】‎ ‎2．(2009年泸州)如图1，在边长为1的等边△ABC中，中线AD与中线BE相交于点O，则OA长度为 ．‎ ‎【关键词】等边三角形．‎ ‎【答案】‎ ‎3．（2009年泸州）如图2，已知Rt△ABC中，AC＝3，BC＝ 4，过直角顶点C作 CA1⊥AB，垂足为A1，再过A1作A‎1C1⊥BC，垂足为C1，过C1作C‎1A2⊥AB，‎ 垂足为A2，再过A2作A‎2C2⊥BC，垂足为C2，…，这样一直做下去，得到了一组 线段CA1，A‎1C1，，…，则CA1＝ ， ‎ ‎【关键词】勾股定理．‎ ‎【答案】，．‎ ‎4．（2009年滨州）某楼梯的侧面视图如图4所示，其中米，，‎ ‎，因某种活动要求铺设红色地毯，则在AB段 楼梯所铺地毯的长度应为 ．‎ B C A ‎30°‎ ‎【关键词】30°所对的直角边等于斜边的一半，‎ 勾股定理．‎ ‎【答案】（2+2）米．‎ ‎5． （2009年滨州）已知等腰的周长 为10，若设腰长为，则的取值范围 是 ．‎ ‎【关键词】等腰三角形．‎ ‎【答案】2．5＜x＜5．‎ ‎6． (2009年四川省内江市)已知Rt△ABC的周长是，斜边上的中线长是2，则S△ABC＝____________‎ ‎【关键词】边上的中线等于斜边的一半，勾股定理，完全平方公式．‎ ‎【答案】8‎ ‎(2009年黄冈市)11．在△ABC中，AB＝AC，AB的垂直平分线与AC所在的直线相交所得到锐角为50°，则∠B等于_____________度．‎ ‎【关键词】等腰三角形 ‎【答案】或 ‎7．(2009年安顺)图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的。在Rt△ABC中，若直角边AC＝6，BC＝6，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长（图乙中的实线）是______________。‎ ‎【关键词】勾股定理 ‎【答案】76 ‎ ‎8．（2009年湖南长沙）如图，等腰中，，是底边上的高，若，则 cm．‎ A C D B ‎【答案】4 ‎ ‎【解析】本题考查了等腰三角形的性质和勾股定理。根据等腰三角形的三线合一可得：，在直角三角形ABD中，由勾股定理得：,所以，。‎ ‎9． （2009襄樊市）在中，为的中点，动点从点出发，以每秒1的速度沿的方向运动．设运动时间为，那么当 秒时，过、两点的直线将的周长分成两个部分，使其中一部分是另一部分的2倍．‎ 解析：本题考查等腰三角形中的动点问题，两种情况，①当点P在BA上时，BP＝t，AP＝12-t，2（t+3）＝12-t+12+3，解得t＝7；②当点P在AC上时， PC＝24-t，t+3＝2（24-t+3），解得t＝17，故填7或17。　‎ ‎【关键词】等腰三角形的性质 ‎【答案】7或17‎ ‎10．（2009年浙江省绍兴市）如图，小量角器的零度线在大量角器的零度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点在小量角器上对应的度数为，那么在大量角器上对应的度数为__________（只需写出～的角度）．‎ ‎ ‎ ‎【关键词】等腰三角形的性质 ‎【答案】50°‎ ‎11．（2009年娄底）如图6，已知AB是⊙O的直径，PB是⊙O的切线，PA交⊙O于C，AB＝‎3cm，PB＝‎4cm，则BC＝ ． ‎【关键词】勾股定理、切线的性质 ‎【答案】‎ ‎ 12．（贵州安顺）图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．在Rt△ABC中，若直角边AC＝6，BC＝5，将四个直角三角形中边长为6的直角边向外延长一倍，得到图乙所示的“数学风车”，则这个风车外围周长（图乙中的实线）是_____76_____．‎ ‎13．（2009年浙江省湖州市）如图，已知在中，，，分别以，为直径作半圆，面积分别记为，，则+的值等于 ．‎ C A B S1‎ S2‎ 关键词】勾股定理，半圆 ‎【答案】2π ‎14． （2009年宜宾）已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3,则图中阴影部分的面积为 ．‎ ‎【关键词】勾股定理 ‎【答案】．‎ ‎15．（2009年长沙）如图，是的直径，是上一点，，则的度数为 ．‎ C B A O 答案：22°‎ ‎【关键词】圆、角 ‎16．（2009年长沙）如图，等腰中，，是底边上的高，若，则 cm．‎ A C D B 答案：4‎ ‎【关键词】等腰三角形 ‎17．(2009年湖州)如图，已知在中，，，分别以，为直径作半圆，面积分别记为，，则+的值等于 ．‎ C A B S1‎ S2‎ ‎【关键词】勾股定理，圆的面积 ‎【答案】‎ ‎18．（2009临沂）如图，过原点的直线l与反比例函数的图象交于M，N两点，根据图象猜想线段MN的长的最小值是___________．‎ O y x M N l ‎【关键词】反比例函数，勾股定理 ‎【答案】‎ ‎19．（2009年漳州）如图，在菱形中，，、分别是、的中点，若，则菱形的边长是_____________．‎ ‎【关键词】三角形中位线定理，等边三角形 ‎【答案】4‎ ‎20． （2009年重庆市江津区）等腰三角形一腰上的高与另一腰的夹角为30º，腰长为‎4 cm，则其腰上的高为 ‎ cm．‎ ‎【关键词】等腰三角形的性质 ‎【答案】‎ ‎21．（2009年）如图，甲、乙两楼相距‎20米，甲楼高‎20米，小明站在距甲楼‎10米的 处目测得点 与甲、乙楼顶刚好在同一直线上，若小明的身高忽略不计，则乙楼的高度是 米．‎ ‎20米 乙 C B A 甲 ‎10米 ‎？米 ‎20米 ‎【关键词】勾股定理 ‎【答案】‎ ‎22．（2009年安徽）13、长为‎4m的梯子搭在墙上与地面成45°角，作业时调整为60°角（如图所示），‎ 则梯子的顶端沿墙面升高了 m．‎ ‎【关键词】勾股定理 ‎【答案】‎ ‎23．（2009年山东青岛市）如图，长方体的底面边长分别为‎1cm 和‎3cm，高为‎6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要 cm；如果从点A开始经过4个侧面缠绕圈到达点B，那么所用细线最短需要 cm．‎ B A ‎6cm ‎3cm ‎1cm ‎【关键词】直角三角形的有关计算、勾股定理 ‎【答案】10，（或）‎ ‎24．（2009年邵阳市）如图所示的圆锥主视图是一个等边三角形，边长为2，则这外圆锥的侧面积为______（结果保留π）。‎ ‎【关键词】等边三角形；勾股定理 ‎【答案】‎ ‎25．(2009年云南省)如图，在Rt△ABC中，∠ACB＝90°，∠BAC的平分线AD交BC于点D，DE∥AC，DE交AB于点E ，M为BE的中点，连结DM． 在不添加任何辅助线和字母的情况下，图中的等腰三角形是 ．（写出一个即可）‎ B D C E M A ‎【关键词】等腰三角形 ‎ ‎【答案】△MBD或△MDE或△EAD ‎26．（2009辽宁朝阳）如图，是等边三角形，点是边上任意一点，于点，于点．若，则_____________．‎ ‎【关键词】正三角形与面积 ‎【答案】‎ F E B C D A 三、解答题 ‎1．（2009年崇左）如图，在等腰梯形ABCD中，已知AD//BC，AB＝DC,AD＝2,BC＝4，延长BC到E，使CE＝AD．‎ ‎（1）证明：ΔBAD≌ΔDCE；‎ ‎（2）如果AC⊥BD，求等腰梯形ABCD的高DF的值．‎ D A B E C F ‎（第24题）‎ ‎【关键词】在等腰梯形性质进行转化。‎ ‎【答案】‎ ‎（1）证明：．‎ 又四边形是等腰梯形，，‎ ‎．‎ ‎．‎ ‎（2）四边形是平行四边形，‎ ‎．‎ ‎．‎ 由（1）可知，，．‎ 所以，是等腰直角三角形，即，‎ ‎．‎ 四边形是等腰梯形，而，‎ ‎．‎ ‎．‎ ‎．（2009年浙江省绍兴市）如图，在中，，分别以为边作两个等腰直角三角形和，使．‎ ‎（1）求的度数；‎ ‎（2）求证：． ‎ ‎ ‎ ‎【关键词】等腰三角形的性质 ‎【答案】（1）ΔABD是等腰直角三角形，，所以∠ABD＝45°,AB＝AC,所以∠ABC＝70°,所以∠CBD＝70°+45°＝115°．‎ ‎(2)AB＝AC,,AD＝AE,所以ΔBAD≌ΔCAE,所以BD＝CE．‎ ‎2．（2009年宁波市）如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为，直线BC经过点，，将四边形OABC绕点O按顺时针方向旋转 度得到四边形，此时直线、直线分别与直线BC相交于点P、Q．‎ ‎（1）四边形OABC的形状是 ，‎ 当时，的值是 ；‎ ‎（2）①如图2，当四边形的顶点落在轴正半轴时，求的值；‎ ‎②如图3，当四边形的顶点落在直线上时，求的面积．‎ ‎（3）在四边形OABC旋转过程中，当时，是否存在这样的点P和点Q，使？若存在，请直接写出点P的坐标；若不存在，请说明理由．‎ ‎（Q）‎ C B A O x P ‎（图3）‎ y Q C B A O x P ‎（图2）‎ y C B A O y x ‎（备用图）‎ ‎【关键词】勾股定理 ‎【答案】解：（1）矩形（长方形）； ‎ ‎．‎ ‎（2）①，，‎ ‎．‎ ‎，即，‎ ‎，．‎ 同理，‎ ‎，即，‎ ‎，． ‎ ‎． ‎ ‎②在和中，‎ ‎．‎ ‎．‎ 设，‎ 在中， ，解得．‎ ‎． ‎ ‎（3）存在这样的点和点，使． ‎ 点的坐标是，． ‎ 对于第（3）题，我们提供如下详细解答，对学生无此要求．‎ 过点画于，连结，则，‎ ‎，，‎ ‎．‎ 设，‎ ‎，‎ ① 如图1，当点P在点B左侧时， ‎ ‎，‎ 在中，，‎ Q C B A O x P y H Q C B A O x P y H 解得，（不符实际，舍去）．‎ ‎，‎ ‎．‎ ‎②如图2，当点P在点B右侧时，‎ ‎，．‎ 在中，，解得．‎ ‎，‎ ‎．‎ 综上可知，存在点，，使．‎ ‎3．(2009年义乌)如图，在边长为4的正三角形ABC中，ADBC于点D，‎ 以AD为一边向右作正三角形ADE。‎ ‎（1）求的面积S；‎ ‎（2）判断AC、DE的位置关系，并给出证明。‎ ‎【关键词】正三角形 ‎【答案】‎ 解：（1）在正中，，‎ ‎．‎ ‎（2）的位置关系：．‎ 在中，，‎ ‎，‎ ‎．‎ ‎4．（2009恩施市）恩施州自然风光无限，特别是以“雄、奇、秀、幽、险”著称于世．著名的恩施大峡谷和世界级自然保护区星斗山位于笔直的沪渝高速公路同侧，、到直线的距离分别为和，要在沪渝高速公路旁修建一服务区，向、两景区运送游客．小民设计了两种方案，图（1）是方案一的示意图（与直线垂直，垂足为），到、的距离之和，图（2）是方案二的示意图（点关于直线的对称点是，连接交直线于点），到、的距离之和．‎ ‎（1）求、，并比较它们的大小；‎ ‎（2）请你说明的值为最小；‎ ‎（3）拟建的恩施到张家界高速公路与沪渝高速公路垂直，建立如图（3）所示的直角坐标系，到直线的距离为，请你在旁和旁各修建一服务区、，使、、‎ ‎、组成的四边形的周长最小．并求出这个最小值．‎ B A P X 图（1）‎ Y X B A Q P O 图（3）‎ B A P X 图（2）‎ ‎【关键词】勾股定理、对称、设计方案 ‎【答案】‎ ‎ 解:⑴图10（1）中过B作BC⊥AP,垂足为C,则PC＝40,又AP＝10,‎ ‎∴AC＝30 ‎ 在Rt△ABC 中，AB＝‎50 AC＝30 ∴BC＝40 ‎ ‎∴ BP＝‎ S1＝ ‎ ‎⑵图10（2）中，过B作BC⊥AA′垂足为C，则A′C＝50，‎ 又BC＝40‎ ‎∴BA'＝‎ 由轴对称知：PA＝PA'‎ ‎∴S2＝BA'＝ ‎ ‎∴﹥ ‎ ‎(2)如 图10（2），在公路上任找一点M,连接MA,MB,MA'，由轴对称知MA＝MA'‎ ‎∴MB+MA＝MB+MA'﹥A'B ‎∴S2＝BA'为最小 ‎（3）过A作关于X轴的对称点A', 过B作关于Y轴的对称点B'，‎ 连接A'B',交X轴于点P, 交Y轴于点Q,则P,Q即为所求 过A'、 B'分别作X轴、Y轴的平行线交于点G,‎ A'B'＝‎ ‎∴所求四边形的周长为 以下是湖北孔小朋的分类：‎ ‎5．（2009年甘肃庆阳）（8分）如图14，在平面直角坐标系中，等腰Rt△OAB斜边OB在y轴上，且OB＝4．‎ ‎（1）画出△OAB绕原点O顺时针旋转90°后得到的三角形；‎ ‎（2）求线段OB在上述旋转过程中所扫过部分图形的面积（即旋转前后OB与点B轨迹所围成的封闭图形的面积）．‎ 图14‎ ‎【关键词】平面直角坐标系；旋转 ‎【答案】本小题满分8分 解：（1）画图正确（如图）；‎ ‎（2）所扫过部分图形是扇形，它的面积是：‎ ‎．‎ ‎6．（2009年河南）如图所示，∠BAC＝∠ABD,AC＝BD，点O是AD、BC的交点，点E是AB的中点．试判断OE和AB的位置关系,并给出证明．‎ ‎【关键词】等腰三角形的性质与判定 ‎【答案】OE⊥AB．　　　　　　　　　　　‎ 证明：在△BAC和△ABD中，‎ AC＝BD，‎ ‎∠BAC＝∠ABD，‎ AB＝BA．‎ ‎ ∴△BAC≌△ABD．　　　‎ ‎∴∠OBA＝∠OAB,‎ ‎∴OA＝OB．　　　　　　　　　　‎ 又∵AE＝BE, ∴OE⊥AB．‎ ‎7．（2009泰安）如图所示，在直角梯形ABCD中，∠ABC＝90°，AD∥BC，AB＝BC，E是AB的中点，CE⊥BD。‎ （1） 求证：BE＝AD；‎ （2） 求证：AC是线段ED的垂直平分线；‎ （3） ‎△DBC是等腰三角形吗？并说明理由。‎ （4） ‎【关键词】直角梯形、垂直平分线、等腰三角形 ‎【答案】证明：（1）∵∠ABC＝90°，BD⊥EC，‎ ‎∴∠1与∠3互余，∠2与∠3互余，‎ ‎∴∠1＝∠2‎ ‎∵∠ABC＝∠DAB＝90°，AB＝AC ‎∴△BAD≌△CBE ‎∴AD＝BE ‎（2）∵E是AB中点，‎ ‎∴EB＝EA 由（1）AD＝BE得：AE＝AD ‎∵AD∥BC ‎∴∠7＝∠ACB＝45°‎ ‎∵∠6＝45°‎ ‎∴∠6＝∠7‎ 由等腰三角形的性质，得：EM＝MD，AM⊥DE。‎ 即，AC是线段ED的垂直平分线。‎ ‎（3）△DBC是等腰三角（CD＝BD）‎ 理由如下：‎ 由（2）得：CD＝CE 由（1）得：CE＝BD ‎∴CD＝BD ‎∴△DBC是等腰三角形。‎ ‎8．（2009年新疆）如图是用硬纸板做成的四个全等的直角三角形，两直角边长分别是，斜边长为和一个边长为的正方形，请你将它们拼成一个能证明勾股定理的图形．‎ ‎（1）画出拼成的这个图形的示意图．‎ ‎（2）证明勾股定理．‎ c b a c b a c b a c b a c c ‎【关键词】勾股定理的验证 ‎【答案】方法一解：（1）如图 a b c c c c b b b a a a a b c ‎（2）证明：大正方形的面积表示为,大正方形的面积也可表示为,，，．即直角三角形两直角边的平方和等于斜边的平方．‎ 方法二解：（1）如图 ‎（2）证明：大正方形的面积表示为：，又可以表示为：,‎ ‎，，．即直角三角形两直角边的平方和等于斜边的平方．‎ ‎9．(2009年牡丹江市)有一块直角三角形的绿地，量得两直角边长分别为现在要将绿地扩充成等腰三角形，且扩充部分是以为直角边的直角三角形，求扩充后等腰三角形绿地的周长．‎ ‎【关键词】勾股定理的应用 ‎【答案】在中，由勾股定理有：，扩充部分为扩充成等腰应分以下三种情况：①如图1，当时，可求,得的周长为‎32m．②如图2，当时，可求,由勾股定理得：,得的周长为③如图3，当为底时，设则由勾股定理得：,得的周长为 A D C B A D B C A D B C 图1‎ 图2‎ 图3‎ ‎10．（2009白银市）如图13，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点，求证：‎ ‎（1）；（2）．‎ ‎【关键词】全等三角形的判定、勾股定理 ‎【答案】27．证明:（1） ∵ ，‎ ‎∴ ．‎ 即 ‎ ‎∵ ， ‎ ‎∴ △ACE≌△BCD ‎（2）∵ 是等腰直角三角形，‎ ‎∴ ．‎ ‎∵ △ACE≌△BCD， ∴ ．‎ ‎∴ ．‎ ‎∴ ．‎ 由（1）知AE＝DB，‎ ‎11．（2009年衡阳市）如图，△ABC中，AB＝AC，AD、AE分别是∠BAC和∠BAC和外角的平分线，BE⊥AE．‎ ‎（1）求证：DA⊥AE；‎ ‎（2）试判断AB与DE是否相等？并证明你的结论．‎ ‎ 【关键词】等腰三角形、矩形 A B C D E F ‎ ‎ ‎【答案】解：（1）证明：‎ ‎（2）AB＝DE，理由是：‎ ‎12．（山东省临沂市）‎ 如图，A，B是公路l（l为东西走向）两旁的两个村庄，A村到公路l的距离AC＝‎1km，B村到公路l的距离BD＝‎2km，B村在A村的南偏东方向上．‎ ‎（1）求出A，B两村之间的距离；‎ ‎（2）为方便村民出行，计划在公路边新建一个公共汽车站P，要求该站到两村的距离相等，请用尺规在图中作出点P的位置（保留清晰的作图痕迹，并简要写明作法）‎ 北 东 B A C D l 解：（1）方法一：设与的交点为，根据题意可得．‎ 和都是等腰直角三角形．‎ ‎，．‎ 两村的距离为（km）．‎ 方法二：过点作直线的平行线交的延长线于．‎ 易证四边形是矩形，‎ ‎．‎ 在中，由，可得．‎ ‎（km）‎ 两村的距离为km．‎ B A C D l N M O P ‎（2）作图正确，痕迹清晰．‎ 作法：①分别以点为圆心，以大于的长为 半径作弧，两弧交于两点，‎ 作直线；‎ ‎②直线交于点，点即为所求． （7分 ‎13．（四川省泸州市）在某段限速公路BC上(公路视为直线)，交通管理部门规定汽车的最高行驶速度不能超过60千米／时 (即米／秒)，并在离该公路‎100米 处设置了一个监测点A．在如图8所示的直角坐标系中，点A位于轴上，测速路段BC在轴上，点B在A的北偏西60°方向上，点C在A的北偏东45°方向上，另外一条高等级公路在轴上，AO为其中的一段．‎ ‎(1)求点B和点C的坐标；‎ ‎(2)一辆汽车从点B匀速行驶到点C所用的时间是15秒，通过计算，判断该汽车在这段限速路上是否超速?(参考数据：)‎ ‎(3)若一辆大货车在限速路上由C处向西行驶，一辆小汽车在高等级公路上由A处向北行驶，设两车同时开出且小汽车的速度是大货车速度的2倍，求两车在匀速行驶过程中的最近距离是多少?‎ 解：在RtΔAOB中，OA＝100,∠BAO＝60°‎ 所以OB＝OA·tan∠BAO＝100．‎ RtΔAOC中,∠CAO＝45°‎ 所以OC＝OA＝100,‎ 所以B(-100,0),C（100，0）‎ ‎（2）BC＝BO+CO＝100+100,‎ ‎18>,‎ 所以这辆车超速了。‎ ‎（3）高大货车行驶到某一时刻行驶了x米，则此时小汽四行驶 了2x米，且两车的距离为 ‎＝‎ 当x＝60时，y有最小值是米，‎ 答：两四相距的最近距离为米．‎ ‎14．（2009年重庆）作图，请你在下图中作出一个以线段AB为一边的等边．（要求：用尺规作图，并写出已知、求作，保留作图痕迹，不写作法和结论）‎ A B ‎19题图 已知：‎ 求作：‎ ‎【关键词】等边三角形, 尺规作图 ‎【答案】‎ 解：已知：线段．‎ 求作：等边．‎ 作图如下：（注：每段弧各1分，连接线段各1分）‎ A B C ‎15．（2009年重庆）已知：如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且．‎ ‎（1）求证：；‎ ‎（2）若，求AB的长．‎ D C E B G A F ‎【关键词】勾股定理、直角三角形性质、等腰三角形性质和全等三角形的判定方法 ‎【答案】（1）证明：于点，‎ ‎．‎ ‎，‎ ‎．‎ 连接，‎ AG＝AG,AB＝AF，‎ ‎．‎ ‎．‎ ‎（2）解：∵AD＝DC,DF⊥AC，‎ ‎．‎ ‎．‎ ‎，‎ ‎．‎ ‎．‎ D C E B G A F ‎16．（2009年广西钦州）已知：如图2，⊙O1与坐标轴交于A（1，0）、B（5，0）两点，点O1的纵坐标为．求⊙O1的半径．‎ ‎【关键词】垂径定理、勾股定理 ‎【答案】‎ 解：过点O1作O‎1C⊥AB，垂足为C，‎ 则有AC＝BC．‎ 由A（1，0）、B（5，0），得AB＝4，∴AC＝2．‎ 在中，∵O1的纵坐标为，‎ ‎∴O‎1C＝．‎ ‎∴⊙O1的半径O‎1A＝＝3．‎ ‎17．(2009年甘肃定西)如图13，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点，求证：（1）；（2）．‎ ‎【关键词】全等三角形、勾股定理 ‎【答案】证明:（1） ∵ ，‎ ‎∴ ．‎ 即 ．‎ ‎∵ ， ‎ ‎∴ △ACE≌△BCD．‎ ‎（2）∵ 是等腰直角三角形，‎ ‎∴ ．‎ ‎∵ △ACE≌△BCD， ∴ ．‎ ‎∴ ．‎ ‎∴ ．‎ 由（1）知AE＝DB，‎ ‎∴ ．‎ ‎18．（2009年莆田）已知：等边的边长为．‎ 探究（1）：如图１，过等边的顶点依次作的垂线围成求证：是等边三角形且； ‎ 探究（2）：在等边内取一点，过点分别作垂足分别为点 ‎ ‎①如图2，若点是的重心，我们可利用三角形面积公式及等边三角形性质得到两个正确结论（不必证明）：结论1．；结论2．；‎ ‎②如图3，若点是等边内任意一点，则上述结论是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由．‎ N M A G C B A F C E B D A F C E B D ‎（图1）‎ ‎（图2）‎ ‎（图3）‎ O A F C E B D ‎（图4）‎ O O ‎【关键词】等边三角形 证明：如图1，为等边三角形 ‎∴‎ N M A G C B ‎（图1）‎ 同理：‎ 为等边三角形．‎ 在中，‎ 在中，‎ ‎（2）：结论1成立．‎ A F C E B D ‎（图2）‎ O H 证明；方法一：如图2，连接 由＝ ‎ 作垂足为，‎ 则 方法二：如图3，过点作分别交于点，过点 作于点，‎ 是等边三角形 四边形是矩形 在中，‎ A F C E B D O M H G 在中，‎ 在中，‎ ‎ ‎ A F C E B D O M G N ‎（2）结论2成立．‎ 证明：方法一：如图４，过顶点依次作边的垂线围成由（1）得为等边三角形且 过点分别作于,于于点于点 由结论1得： ‎ 又 四边形为矩形 同理：，‎ 方法二：（同结论1方法二的辅助线）‎ A F C E B D ‎（图3）‎ O M H G 在中，‎ 在中，‎ 同理：‎ ‎＝‎ ‎＝‎ 由结论1得：‎ A F C E B D ‎（图5）‎ O 方法三：如图5，连接，根据勾股定理得：‎ ‎：‎ 整理得：‎ ‎ 12分 ‎20．(2009年南充)如图8，半圆的直径，点C在半圆上，．‎ ‎（1）求弦的长；‎ ‎（2）若P为AB的中点，交于点E，求的长．‎ P B C E A ‎【关键词】圆的性质，三角形相似的性质 ‎【答案】解：是半圆的直径，点在半圆上，‎ ‎．‎ 在中， ‎ ‎（2），‎ ‎．，‎ ‎．‎ 又，‎ ‎，‎ ‎．‎ ‎19．(2009年湖州)如图，在平面直角坐标系中，直线∶＝分别与轴，轴相交于两点，点是轴的负半轴上的一个动点，以为圆心，3为半径作 ‎．‎ ‎（1）连结，若，试判断与轴的位置关系，并说明理由；‎ ‎（2）当为何值时，以与直线的两个交点和圆心为顶点的三角形是正三角形？‎ B A O x l y P A O x l y ‎（备用图）‎ ‎【关键词】直线与圆的位置关系，相切的判定，正三角形的性质，相似的性质 ‎【答案】‎ 第（1）题 B A O x l y P B A O x l y C E D P1‎ P2‎ 第（2）题 解：（1）与轴相切．‎ 直线与轴交于，与轴交于，‎ ‎，‎ 由题意，．‎ 在中，，‎ 等于的半径，与轴相切． ‎ ‎（2）设与直线交于两点，连结．‎ 当圆心在线段上时，作于．‎ 为正三角形，．‎ ‎，‎ 即，‎ ‎，‎ ‎．‎ 当圆心在线段延长线上时，同理可得，‎ ‎，‎ ‎ 当或时，以与直线的两个交点和圆心为顶点的三角形是正三角形．‎ ‎20．(2009年湖州)若P为所在平面上一点，且，则点叫做的费马点．‎ ‎（1）若点为锐角的费马点，且，则的值为________；‎ ‎（2）如图，在锐角外侧作等边′连结′．‎ 求证：′过的费马点，且′＝．‎ A C B ‎【关键词】阅读理解题，等边三角形的性质，全等三角形的判定及性质，综合题 ‎【答案】（1）2． ‎ ‎（2）‎ A C B P E 证明：在上取点，使，‎ 连结，再在上截取，连结．‎ ‎，‎ 为正三角形，‎ ‎＝，‎ 为正三角形，‎ ‎＝，‎ ‎＝，‎ ‎′，‎ ‎．‎ ‎，‎ ‎，‎ 为的费马点，‎ 过的费马点，且＝+．‎ ‎21．(2009年温州)如图，在△ABC中，∠C＝90°，AC＝3，BC＝4．0为BC边上一点，以0为圆心，OB为半径作半圆与BC边和AB边分别交于点D、点E，连结DE． ’‎ ‎ (1)当BD＝3时，求线段DE的长；‎ ‎ (2)过点E作半圆O的切线，当切线与AC边相交时，设交点为F．求证：△FAE是等腰三角形．‎ ‎【关键词】直角三角形、圆的性质，相似的判定，切线的性质，等腰三角形的判定 ‎【答案】解：（1）∵∠C＝90°，AC＝3，BC＝4，‎ ‎∴AB＝5，‎ ‎∵DB为直径，‎ ‎∴∠DEB＝∠C＝90°，‎ 又∵∠B＝∠B ，∴△DBE∽△ABC ‎∴ 即 ‎∴DE＝。‎ ‎（2）解法一：连结OE，‎ ‎∵EF为半圆O的切线，‎ ‎∴∠DEO+∠DEF＝90°，‎ ‎∵∠AEF+∠DEF＝90°，‎ ‎∴∠AEF＝∠DEO，‎ ‎∵△DBE∽△ABC，‎ ‎∴∠A＝∠EDB，‎ 又∵∠EDO＝∠DEO，‎ ‎∴∠AEF＝∠A，‎ ‎∴△FAE是等腰三角形。‎ 解法二：连结OE，‎ ‎∵EF为半圆O的切线，‎ ‎∴∠AEF+∠OEB＝90°，‎ ‎∵∠C＝90°，‎ ‎∴∠A+∠B＝90°，‎ ‎∵OE＝OB ‎∴∠OEB＝∠B，‎ ‎∴∠AEF＝∠A ‎∴△FAE是等腰三角形。‎ ‎22．（2009临沂）如图，A，B是公路l（l为东西走向）两旁的两个村庄，A村到公路l的距离AC＝‎1km，B村到公路l的距离BD＝‎2km，B村在A村的南偏东方向上．‎ ‎（1）求出A，B两村之间的距离；‎ ‎（2）为方便村民出行，计划在公路边新建一个公共汽车站P，要求该站到两村的距离相等，请用尺规在图中作出点P的位置（保留清晰的作图痕迹，并简要写明作法）．‎ 北 东 B A C D l ‎【关键词】等腰直角三角形的性质，勾股定理，尺规作图 ‎【答案】解：（1）方法一：设与的交点为，根据题意可得．‎ 和都是等腰直角三角形．‎ ‎，．‎ 两村的距离为（km）．‎ 方法二：过点作直线的平行线交的延长线于．‎ 易证四边形是矩形，‎ ‎．‎ 在中，由，可得．‎ ‎（km）‎ 两村的距离为km．‎ ‎（2）作图正确，痕迹清晰．‎ B A C D l N M O P 作法：①分别以点为圆心，以大于的长为 半径作弧，两弧交于两点，‎ 作直线；‎ ‎②直线交于点，点即为所求．‎ ‎1．（2009年中山）如图所示，是等边三角形， 点是的中点，延长到，使，‎ ‎（1）用尺规作图的方法，过点作，垂足是（不写作法，保留作图痕迹）；‎ ‎（2）求证：．‎ ‎【关键词】等腰三角形，等边三角形 ‎【答案】解：（1）作图见下图，‎ A C B D E M ‎（2）是等边三角形，是的中点，‎ 平分（三线合一），‎ ‎．‎ ‎，‎ ‎．‎ 又，‎ ‎．‎ 又，‎ ‎，‎ ‎，‎ ‎．‎ 又，‎ ‎．‎ ‎23．（2009年牡丹江）有一块直角三角形的绿地，量得两直角边长分别为现在要将绿地扩充成等腰三角形，且扩充部分是以为直角边的直角三角形，求扩充后等腰三角形绿地的周长．‎ ‎【关键词】等腰三角形，勾股定理 ‎【答案】在中，‎ 由勾股定理有：，扩充部分为扩充成等腰应分以下三种情况．‎ ‎ ①如图1，当时，可求 ‎ 得的周长为‎32m．‎ ‎②如图2，当时，可求 由勾股定理得：，得的周长为 ‎③如图3，当为底时，设则 由勾股定理得：，得的周长为 A D C B A D B C A D B C 图1‎ 图2‎ 图3‎ ‎24．(2009年宁德市)（本题满分13分）如图，已知抛物线C1：的顶点为P，与x轴相交于A、B两点（点A在点B的左边），点B的横坐标是1．‎ ‎（1）求P点坐标及a的值；（4分）‎ ‎（2）如图（1），抛物线C2与抛物线C1关于x轴对称，将抛物线C2向右平移，平移后的抛物线记为C3，C3的顶点为M，当点P、M关于点B成中心对称时，求C3的解析式；（4分）‎ ‎（3）如图（2），点Q是x轴正半轴上一点，将抛物线C1绕点Q旋转180°后得到抛物线C4．抛物线C4的顶点为N，与x轴相交于E、F两点（点E在点F的左边），当以点P、N、F为顶点的三角形是直角三角形时，求点Q的坐标．（5分）‎ y x A O B P N 图2‎ C1‎ C4‎ Q E F 图（2）‎ y x A O B P M 图1‎ C1‎ C2‎ C3‎ 图（1）‎ ‎【关键词】二次函数,勾股定理的运用 y x A O B P M 图(1)‎ C1‎ C2‎ C3‎ H G 解：（1）由抛物线C1：得 顶点P的为（-2，-5） ‎ ‎∵点B（1，0）在抛物线C1上 ‎∴‎ ‎ 解得，a＝ ‎ ‎（2）连接PM，作PH⊥x轴于H，作MG⊥x轴于G ‎∵点P、M关于点B成中心对称 ‎∴PM过点B，且PB＝MB ‎∴△PBH≌△MBG ‎∴MG＝PH＝5，BG＝BH＝3‎ ‎∴顶点M的坐标为（4，5） ‎ ‎ 抛物线C2由C1关于x轴对称得到，抛物线C3由C2平移得到 ‎∴抛物线C3的表达式为 ‎ ‎（3）∵抛物线C4由C1绕点x轴上的点Q旋转180°得到 ‎∴顶点N、P关于点Q成中心对称 ‎ 由（2）得点N的纵坐标为5‎ 设点N坐标为（m，5） ‎ y x A O B P N 图(2)‎ C1‎ C4‎ Q E F H G K ‎ ‎ ‎ 作PH⊥x轴于H，作NG⊥x轴于G ‎ 作PK⊥NG于K ‎ ∵旋转中心Q在x轴上 ‎∴EF＝AB＝2BH＝6‎ ‎ ∴FG＝3，点F坐标为（m+3，0）‎ ‎ H坐标为（2，0），K坐标为（m，-5），‎ 根据勾股定理得 ‎ PN2＝NK2+PK2＝m2+‎4m+104‎ ‎ PF2＝PH2+HF2＝m2+‎10m+50‎ ‎ NF2＝52+32＝34 ‎ ‎ ①当∠PNF＝90º时，PN2+ NF2＝PF2，解得m＝，∴Q点坐标为（，0） ‎ ‎②当∠PFN＝90º时，PF2+ NF2＝PN2，解得m＝，∴Q点坐标为（，0）‎ ‎③∵PN＞NK＝10＞NF，∴∠NPF≠90º 综上所得，当Q点坐标为（，0）或（，0）时，以点P、N、F为顶点 的三角形是直角三角形． ‎ ‎25．(2009年河北)图10是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且CD ＝ ‎24 m，‎ OE⊥CD于点E．已测得sin∠DOE ＝ ．‎ ‎（1）求半径OD；‎ ‎（2）根据需要，水面要以每小时0．‎5 m的速度下降，则经过多长时间才能将水排干？‎ A O B 图10‎ E C D ‎ ‎ ‎【关键词】解直角三角形,勾股定理,‎ 解：（1）∵OE⊥CD于点E，CD＝24，‎ ‎∴ED ＝＝12．‎ ‎ 在Rt△DOE中，‎ ‎∵sin∠DOE ＝ ＝，‎ ‎∴OD ＝13（m）． ‎ ‎ （2）OE＝‎ ‎＝．‎ ‎ ∴将水排干需：‎ ‎5÷0．5＝10（小时）． ‎ ‎26．(2009年潍坊)在四边形中，，且．取的中点，连结．‎ ‎（1）试判断三角形的形状；‎ ‎（2）在线段上，是否存在点，使．若存在，请求出的长；若不存在，请说明理由．‎ P D C B A 解：（1）在四边形中，，，‎ 四边形为直角梯形（或矩形）．‎ 过点作，垂足为，，‎ 又点是的中点，点是的中点，‎ 又，‎ ‎， ‎ 与是全等的等腰直角三角形，‎ ‎，‎ 是等腰直角三角形． ‎ ‎（2）存在点使． ‎ 以为直径，为圆心作圆．‎ 当时，四边形为矩形，，‎ 圆与相切于点，此时，点与点重合，存在点，使得，‎ 此时． ‎ 当时，四边形为直角梯形，‎ ‎，，圆心到的距离小于圆的半径，圆与相交，上存在两点，使， ‎ 过点作，在中，，‎ 连结，则，‎ 在直角三角形中，，‎ ‎．‎ 同理可得：．‎ 综上所述，在线段上存在点，使．‎ 当时，有一点，；当时，有两点，． ‎ P D C B A Q E M2‎ M1‎ ‎27．（09湖北宜昌）已知：如图， AF平分∠BAC，BC⊥AF， 垂足为E，点D与点A关于点E对称，PB分别与线段CF， AF相交于P，M．‎ ‎(1)求证：AB＝CD；‎ ‎(2)若∠BAC＝2∠MPC，请你判断∠F与∠MCD 的数量关系，并说明理由． ‎ ‎【关键词】全等三角形的性质与判定、等腰三角性的性质 ‎【答案】解：(1)证明：∵AF平分∠BAC， ‎ ‎ ∴∠CAD＝∠DAB＝∠BAC．‎ ‎∵D与A关于E对称，∴E为AD中点．‎ ‎∵BC⊥AD，∴BC为AD的中垂线，∴AC＝CD． ‎ 在Rt△ACE和Rt△ABE中，注：证全等也可得到AC＝CD ‎∠CAD+∠ACE＝∠DAB+∠ABE＝90°， ∠CAD＝∠DAB．‎ ‎∴∠ACE＝∠ABE，∴AC＝AB． 注：证全等也可得到AC＝AB ‎∴AB＝CD． ‎ ‎ ‎ ‎(2)∵∠BAC＝2∠MPC， 又∵∠BAC＝2∠CAD，∴∠MPC＝∠CAD．‎ ‎∵AC＝CD，∴∠CAD＝∠CDA， ∴∠MPC＝∠CDA． ‎ ‎∴∠MPF＝∠CDM． ‎ ‎∵AC＝AB，AE⊥BC，∴CE＝BE． 注：证全等也可得到CE＝BE ‎∴AM为BC的中垂线，∴CM＝BM． 注：证全等也可得到CM＝BM ‎∵EM⊥BC，∴EM平分∠CMB，(等腰三角形三线合一) ‎ ‎∴∠CME＝∠BME． 注：证全等也可得到∠CME＝∠BME ‎ ‎∵∠BME＝∠PMF，‎ ‎∴∠PMF＝∠CME， ‎ ‎∴∠MCD＝∠F(三角形内角和)． 注：证三角形相似也可得到∠MCD＝∠F ‎28．（09湖南怀化）如图12，在直角梯形OABC中， OA∥CB，A、B两点的坐标分别为A（15，0），B（10，12），动点P、Q分别从O、B两点出发，点P以每秒2个单位的速度沿OA向终点A运动，点Q以每秒1个单位的速度沿BC向C运动，当点P停止运动时，点Q也同时停止运动．线段OB、PQ相交于点D，过点D作DE∥OA，交AB于点E，射线QE交轴于点F．设动点P、Q运动时间为t（单位：秒）．‎ ‎（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；‎ ‎（2）当t＝2秒时，求梯形OFBC的面积；‎ ‎（3）当t为何值时，△PQF是等腰三角形？请写出推理过程．‎ ‎【关键词】一元二次方程解法及应用、勾股定理及逆定理、等腰三角形、等腰梯形的判定 ‎【答案】‎ 解：（1）如图4，过B作 则 过Q作 则 要使四边形PABQ是等腰梯形，则，‎ 即 或（此时是平行四边形，不合题意，舍去）‎ ‎（2）当时，。‎ ‎（3）①当时，则 ‎②当时，‎ 即 ‎③当时， ‎ 综上，当时，△PQF是等腰三角形． ‎ ‎29．（09湖南邵阳）如图，在梯形中，，，，将延长至点，使．‎ ‎（1）求的度数；‎ ‎（2）求证：为等腰三角形．‎ D A F B C ‎【关键词】等腰三角性的性质与判定、等腰梯形的性质 ‎【答案】（1）‎ ‎．‎ 在中， ‎ ‎；‎ ‎（2）连接．在梯形中，，，‎ 在四边形中，‎ 四边形是平行四边形，，‎ ‎，即为等腰三角形．‎ ‎【关键词】直角三角形的有关计算、勾股定理 ‎【答案】C ‎30．（2009年湖北十堰市）如图，在一次数学课外活动中，小明同学在点P处测得教学楼A位于北偏东60°方向，办公楼B位于南偏东45°方向．小明沿正东方向前进‎60米到达C处，此时测得教学楼A恰好位于正北方向，办公楼B正好位于正南方向．求教学楼A与办公楼B之间的距离（结果精确到0．‎1米）．‎ ‎（供选用的数据：≈1．414，≈1．732）‎ ‎【关键词】直角三角形的有关计算、测量问题、勾股定理 ‎【答案】解：由题意可知 ‎ ∠ACP＝ ∠BCP＝ 90°，∠APC＝30°，∠BPC＝45°…2分 在Rt△BPC中，∵∠BCP＝90°，∠BPC＝45°，∴‎ 在Rt△ACP中，∵∠ACP＝90°，∠APC＝30°，∴ ‎ ‎∴‎ ‎≈60+20×1．732 ＝94．64≈94．6(米) ‎ 答：教学楼A与办公楼B之间的距离大约为94．‎6米．‎ 说明：（1）其它解法请参照上述评分说明给分；（2）不作答不扣分．‎ ‎31．(2009年达州)如图10，⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E，AC∥DE交BD于点H，DO及延长线分别交AC、BC于点G、F．‎ ‎(1)求证：DF垂直平分AC；‎ ‎（2）求证：FC＝CE；‎ ‎（3）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径． ‎ ‎【关键词】圆,平行四边形,勾股定理 ‎【答案】‎ ‎（1）∵DE是⊙O的切线，且DF过圆心O ‎∴DF⊥DE 又∵AC∥DE ‎∴DF⊥AC ‎∴DF垂直平分AC ‎ ‎（2）由（1）知：AG＝GC 又∵AD∥BC ‎∴∠DAG＝∠FCG 又∵∠AGD＝∠CGF ‎∴△AGD≌△CGF（ASA）‎ ‎∴AD＝FC ‎∵AD∥BC且AC∥DE ‎∴四边形ACED是平行四边形 ‎∴AD＝CE ‎∴FC＝CE5分 ‎（3）连结AO； ∵AG＝GC，AC＝‎8cm，∴AG＝‎‎4cm 在Rt△AGD中，由勾股定理得 GD＝AD2-AG2＝52-42＝‎3cm ‎ 设圆的半径为r，则AO＝r，OG＝r-3‎ 在Rt△AOG中，由勾股定理得 AO2＝OG2+AG2‎ 有：r2＝(r-3)2+42解得 r＝256 ‎ ‎∴⊙O的半径为‎256cm．‎ ‎32．（2009年广东省）如图所示，是等边三角形，点是的中点，延长到，使．‎ ‎（1）用尺规作图的方法，过点作，垂足是（不写作法，保留作图痕迹）；‎ ‎（2）求证：．‎ A B C E D ‎【关键词】等边三角形；线段和角的概念、性质、画法及有关计算 ‎【答案】解：（1）作图如下图，‎ A B E D C M ‎（2）是等边三角形，是的中点 平分（三线合一），‎ ‎，‎ ‎，‎ ‎，‎ 又 ‎，‎ 又，‎ ‎，‎ ‎，‎ ‎，‎ 又，‎ ‎33．（2009 黑龙江大兴安岭）在边长为4和6的矩形中作等腰三角形，使等腰三角形的一条边是矩形的长或宽，第三个顶点在矩形的边上，求所作三角形的面积．‎ ‎（注：形状相同的三角形按一种计算．）‎ ‎【关键词】等腰三角形 ‎【答案】． 面积是12,面积是8和12‎ ‎34．（2009年崇左）如图，在等腰梯形中，已知，，延长到，使．‎ ‎（1）证明：；‎ D A B E C F ‎（第24题）‎ ‎（2）如果，求等腰梯形的高的值．‎ ‎【关键词】在等腰梯形性质进行转化。‎ ‎【答案】‎ ‎（1）证明：．‎ 又四边形是等腰梯形，，‎ ‎．‎ ‎．‎ ‎（2）四边形是平行四边形，‎ ‎．‎ ‎．‎ 由（1）可知，，．‎ 所以，是等腰直角三角形，即，‎ ‎．‎ 四边形是等腰梯形，而，‎ ‎．‎ ‎．‎ ‎（2009龙岩）阅读下列材料：‎ 正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．‎ 数学老师给小明同学出了一道题目：在图正方形网格（每个小正方形边长为1）中画出格点△ABC，使，；‎ 小明同学的做法是：由勾股定理，得，，于是画出线段AB、AC、BC，从而画出格点△ABC．‎ ‎（1）请你参考小明同学的做法，在图23－2正方形网格（每个小正方形边长为1）中画出格点△（点位置如图所示），使＝＝5，．（直接画出图形，不写过程）；‎ ‎（2）观察△ABC与△的形状，猜想∠BAC与∠有怎样的数量关系，并证明你的猜想．‎ C B A ‎【关键词】等腰三角形 ‎【答案】（1）正确画出△‎ ‎（画出其中一种情形即可）‎ ‎ （2）猜想：∠BAC ＝∠ ‎ 证明：∵，；‎ ‎∴，‎ ‎∴△ABC ∽ △，‎ ‎∴∠BAC ＝∠ ‎ 等腰三角形 一、 选择题 ‎1、(2011浙江杭州模拟16)下列命题正确的有 ( )个 ‎①400角为内角的两个等腰三角形必相似 ‎②若等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的底角为750‎ ‎③一组对边平行，另一组对边相等的四边形是平行四边形 ‎④一个等腰直角三角形的三边是a、b、c，（a>b=c），那么a2∶b2∶c2=2∶1∶1‎ ‎⑤若△ABC的三边a、b、c满足a2+b2+c2+338=‎10a+24b+‎26c，则此△为等腰直角三角形。‎ A、1个 B、2个 C、3个 D、4个 答案：A ‎2、（11年青岛二中）如图，等边的边长为3，为上一点，且，为上一点，若，则的长为（ ）‎ A． B． C． D．‎ 答案：B ‎3、（2011杭州模拟）如图，在△ABC中，AC＝BC，CD是AB边上的高线，且有2CD=3AB，又E，F为CD的三等分点，则∠ACB和∠AEB之和为： ……………… ( ▲ )‎ A．45° B．90° C． 60° D．75°‎ 答案：B ‎4.(浙江省杭州市党山镇中2011年中考数学模拟试卷)若等腰三角形中有一个角等于，则这个等腰三角形的顶角的度数为（ ）‎ A． B． C．或 D．或 答案：D B组 ‎1. （2011深圳市全真中考模拟一）等腰三角形一腰上的高与另一腰的夹角为30。，则顶角的度数为 ‎(A)60． (B)120． (C)60或150． (D)60或120‎ 答案:D ‎2.（浙江杭州进化2011一模）如图，△ABC内接于⊙O，其外角平分线AD交⊙O于DM⊥AC于M，下列结论：①DB=DC；②AC-AB=2AM；③AC+AB=‎2CM；④=2其中正确的有( )‎ A．只有④② B．只有①②③ C．只有③④ D．①②③④‎ 答案: B A B C D E ‎3、（2011年杭州模拟17）如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的面积为（2010沈阳中考第8题改编） ‎ A. 81 B . 81／‎2 C. 81／4 D. 81／8 ‎ 答案：C 一、 填空题 A D C P B ‎（第1题图）‎ ‎60°‎ ‎1、（2011年北京四中四模）如图，以A、B两点为其中两个顶点作位置不同的等边三角形，最多可以作出_____个. ‎ 答案：2‎ ‎2、（2011北京四中模拟6）用两块完全重合的等腰三角形纸片能拼出下列图形 ‎ .‎ 答案 平行四边形，正方形，等腰直角三角形；‎ ‎3、(2011浙江杭州模拟15)如图，将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD，连结CD.若AB=‎4cm. 则△BCD的面积为　　　　．‎ 答案：‎ P C B A ‎4、(2011浙江杭州模拟15)如图△ABC中，∠ACB＝90°，BC＝‎6 cm，AC＝‎8cm，动点P从A出发，以‎2 cm / s的速度沿AB移动到B，则点P出发 s时，△BCP为等腰三角形． ‎ 答案： 2，2．5，1．4 ‎ ‎5. （2011年江苏盐城）已知△ABC中，AB＝AC，∠B＝70°，则∠C的大小为 ．‎ 答案70° ‎6、（2011年浙江省杭州市模拟）等腰两边的长分别是一元二次方程的两个解，则这个等腰三角形的周长是 ．‎ 答案：7,9 ‎ B组 ‎1. （2011深圳市中考模拟五）等腰三角形的腰长为2，腰上的高为1，则它的底角等于 ．‎ 答案: 15°或75°‎ ‎2．（ 2011年杭州三月月考）若一边长为40㎝的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过，则铁圈直径的最小值为 ▲ ㎝．(铁丝粗细忽略不计)‎ 答案： ‎ ‎3、（北京四中2011中考模拟13）用两块完全重合的等腰三角形纸片能拼出下列图形 .‎ 答案：平行四边形，正方形，等腰直角三角形；‎ A D F C B E ‎（第4题）图）‎ ‎4．（2011年海宁市盐官片一模）如图，有一块边长为4的正方形塑料摸板，将一块足够大的直角三角板的直角顶点落在点，两条直角边分别与交于点，与延长线交于点．则四边形的面积是　　　　　　　．‎ 答案：16‎ A B C D E O 第5题 ‎5. （2011年浙江省杭州市模2） 如图，在半圆O中，直径AE=10，四边形ABCD是平行四边形，且顶点A、B、C在半圆上，点D在直径AE上，连接CE，若AD=8，则CE长为 ． ‎ 答案：‎ 一、 解答题 A组 ‎1、（北京四中模拟7）已知：如图，在DABC中，ÐC=90°，AB的垂直平分线交AC于D，垂足为E.若ÐA=30°，DE=2，求ÐDBC的度数和CD的长.‎ 答案 2 ‎ ‎2、(2011浙江杭州模拟15)‎ 如图（1）矩形纸片ＡＢＣＤ，把它沿对角线折叠，会得到怎么样的图形呢？‎ Ｂ F C A Ｄ E 第2题图 G ‎（1）在图（2）中用实线画出折叠后得到的图形（要求尺规作图，保留作图轨迹，只需画出其中一种情况）‎ A D C B ‎（2）‎ ‎（2）折叠后重合部分是什么图形？试说明理由。 ‎ A D C B ‎（1） ‎ 答案：‎ ‎（1）图略 （4分）‎ ‎（2）等腰三角形 （1分）‎ ‎ （2分）‎ ‎3．（2011年重庆江津区七校联考）已知ａ、ｂ、ｃ分别是△ABC的三边，其中ａ＝1，ｃ＝4，且关于x的方程有两个相等的实数根，试判断△ABC的形状.‎ 答案：‎ ‎∵关于x的方程有两个相等的实数根 ‎　　∴　△＝　　 ‎ ‎　　∴　　　　　　　　　 ‎ ‎　　∴　　　　　　　 ‎ ‎△ABC是等腰三角形.　‎ 等腰三角形 一、选择题 ‎1.（2010年三亚二模）若等腰三角形中有一个角等于，则这个等腰三角形的顶角的度数为（ ）‎ A． B． C．或 D．或 答案：D ‎2.（2010年武汉中考模拟试卷6）如图，已知△ABC中，AB＝AC，∠BAC＝900，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出下列四个结论：①AE＝CF；②△EPF是等腰直角三角形；③EF＝AP；④S四边形AEPF＝S△ABC，当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），上述结论中始终正确的有（ ）。‎ ‎ A.①②③④ B.①②③ C.①②④ D.②③④‎ 答案：C ‎3.（2010普陀区 中考模拟 ）下列条件中，能判定两个等腰三角形相似的是（ ）‎ A.都含有一个30°的内角； B.都含有一个45°的内角；‎ C.都含有一个60°的内角； D.都含有一个80°的内角．‎ 答案：Ｃ ‎4.(昆山2010第二学期调研)在等腰三角形ABC中，AB的长是AC长的2倍，三角形的周长是40，则AB长是( )‎ A．10 B．‎16 ‎‎ C．20 D．16或20‎ 答案：B ‎5.（2010静安区模拟）等边三角形绕它的一个顶点旋转90º后与原来的等边三角形组成一个新的图形，那么这个新的图形 ( )‎ A.是轴对称图形，但不是中心对称图形 B.是中心对称图形，但不是轴对称图形 C.既是轴对称图形，又是中心对称图形 D.既不是轴对称图形，又不是中心对称图形 答案：A ‎6.（2010武汉模拟）如图，△ABC中，AB=AC，BD是△ABC的高，将△BCD沿BD折叠，使C点落在AC上的E处，若∠C=750，则∠ABE的度数为 ( )‎ ‎ A、750 B、‎300 C、450 D、37.50‎ 答案：C 二、填空题 ‎1. (芜湖市2010年九年级毕业暨升学模拟考试) 等腰△ABC中，AB=AC=‎8cm，BC=‎6cm，则内切圆的半径为_________‎ 答案 cm ‎2.（2010年武汉中考模拟试卷）一个顶角为2x的等腰三角形的一个底角度数为 .（用含x的式子表示）‎ 答案：90°-x 三、解答题 ‎1.（2010年武汉中考模拟试卷）已知Rt△ABC中，∠ACB=90°，CA=CB，有一个圆心角为45°，半径长等于CA的扇形CEF绕点C旋转，直线CE、CF分别与直线AB交于点M、N ‎⑴如图①，当AM=BN时，将△ACM沿CM折叠，点A落在弧EF的中点P处，，再将△BCN沿CN折叠，点B也恰好落在点P处，此时，PM=AM，PN=BN，△PMN的形状是 ‎ 线段AM、BN、MN之间的数量关系是 ‎ ‎⑵如图②，当扇形CEF绕点C在∠ACB内部旋转时，线段MN、AM、BN之间的数量关系是 ‎ ，试证明你的猜想；‎ ‎⑶当扇形CEF绕点C旋转至图③的位置时，线段MN、AM、BN之间的数量关系是 ‎ ‎（不要求证明）‎ 答案：(1)等腰直角三角形AM2+BN2=MN2(或AM=BN=√2/2 MN)‎ ‎⑵AM2+BN2=MN2‎ 将△ACM沿CM折叠,得△DCM。连DN，则△ACM≌△DCM，‎ ‎∴CD=CA DM=AM，∠DCM=∠ACM，进而可知∠DCN=∠BCN，‎ △ DCN≌△BCN，DN=BN，而∠MDC=∠A=45°，∠CDN=∠B=45°‎ ‎∴∠MDN=90°∴DM2+DN2=MN2，，故AM2+BN2=MN2‎ ‎⑶AM2+BN2=MN2‎ ‎2.(昆山2010第二学期调研)． 如图所示，△ABC是等边三角形，D点是AC的中点，延长BC到E，使CE=CD．‎ ‎(1)求∠E的度数．‎ ‎ (2)用尺规作图的方法，过D点作DM⊥BE，垂足为M． (不写作法，保留作图痕迹)‎ ‎ (3)求证：BM=EM．‎ 第2题图 ‎3．（2010模拟题二）已知：等腰直角三角形纸片ABC，∠C=90°，BC=AC．将纸片折叠使点A总是落在BC边上,记为点D,EF为折痕(如图).‎ ‎⑴　当△DEF是以∠EDF为顶角的等腰三角形时,试判断△DCF的形状,并说明理由;‎ A C D E F ‎⑵　在BC边上是否存在点D,使折叠后所得的△DEF与△DEB相似?若存在,请求出相似比;若不存在,请说明理由.‎ 解: 解:(1)由折叠知∠1=∠A=45°,∠4=∠2,∵DE=DF ∴∠2=∠3‎ ‎∴∠4=∠3 ∴DF∥AB , ∠5=∠A=45°, ∵∠C=90°, ∴∠6=45° ‎ ‎∴∠6=∠5 ∴DC=CF∴△DCF是等腰直角三角形 ‎ A B C E F ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ D B E C A ‎1‎ ‎2‎ ‎7‎ ‎（D）‎ F E C A ‎2‎ H ‎4‎ ‎8‎ D B F ‎①　　　　　　　　　②‎ ‎(2) ∵∠1=45°∠B=45°∴∠1=∠B ‎ 若∠2=∠7 则△DEF∽△BDE, 如图①,此时BD∥EF,点D与点C重合,‎ ‎∴EF⊥AC,∵∠1=∠A=45°, ∴∠7=45°∵∠B=45°∴∠BEC=90°∴△BEC是等腰直角三角形∴相似比为 　　　　　　　‎ 若∠2=∠8 则△DEF∽△BED, 如图②,‎ 过点D作DH⊥BE于H,∵∠2=∠4 ∴∠2=∠8=∠4=60°‎ 设EH=x,则BH=DH=,DE=2x ‎ ‎∴相似比为 ‎∴在BC上存在点D,使折叠后所得的△DEF与△DEB相似,相似比为或 ‎4.（2010武汉中考模拟1）如图①，已知△ABC中，AB=AC，点P是BC上的一点，PN⊥AC于点N，PM⊥AB于点M，CG⊥AB于点G点。‎ （1） 则CG、PM、PN三者之间的数量关系是_________。 ‎ （2） 如图②，若点Ｐ在ＢＣ的延长线上， 则ＰＭ、ＰＮ、ＣＧ三者是否还有上述关系，若有，请说明理由，若没有，猜想三者之间又有怎样的关系，并证明你的猜想；‎ 第4题图 （3） 如图③，AC是正方形ABCD的对角线,AE=AB, 点P是BE上任一点, PN⊥AB于点N，PM⊥AC于点M，猜想ＰＭ、ＰＮ、ＡＣ有什么关系；（直接写出结论）‎ 答案：(1)CG=PM+PN ‎ ‎ （2）猜想ＣＧ=ＰＭ－ＰＮ．‎ ‎　　 证明：过C点作CE⊥PM于E.‎ ‎　　 ∵PN⊥AB，CG⊥AB，∴四边形CGME是矩形.‎ ‎　　 ∴ME=CG，CE∥AB．‎ ‎　　 ∴∠B=∠ECP. ‎ ‎　 ∵AB=AC，∴∠B=∠ACB=∠PCN.‎ ‎　 　∴∠ECP=∠PCN.‎ ‎　 　∵∠PNC=∠PEC=90°，PC=PC，∴△PNC≌△PEC. ‎ ‎∴PN=PE . ‎ ‎　　 ∴CG= ME=PM－PE=PM－PN .‎ ‎　　（3）PM+PN=AC .‎ ‎　　证明：连接BD，交AC于O，过点P作PF⊥BD于F.‎ ‎　　∵四边形ABCD是正方形，∴∠COB=90°，OB=OC=AC.‎ ‎　　∵PM⊥AC，∴四边形PFOM为矩形.‎ ‎　　∴MP=OF，PF∥AC.∴∠OEP=∠FPB.‎ ‎　　∵AE=AB，∴∠OEP=∠ABP.‎ ‎　　∴∠ABP=∠FPB.‎ ‎　　∵PB=PB，∠PFB=∠PNB=90°，∴△PFB≌△BNP.‎ ‎　　∴BF=PN.∴OB=OF+FB= PM+PN=AC. 　　‎