中考数学专题12三级训练配答案

中考数学专题12三级训练配答案

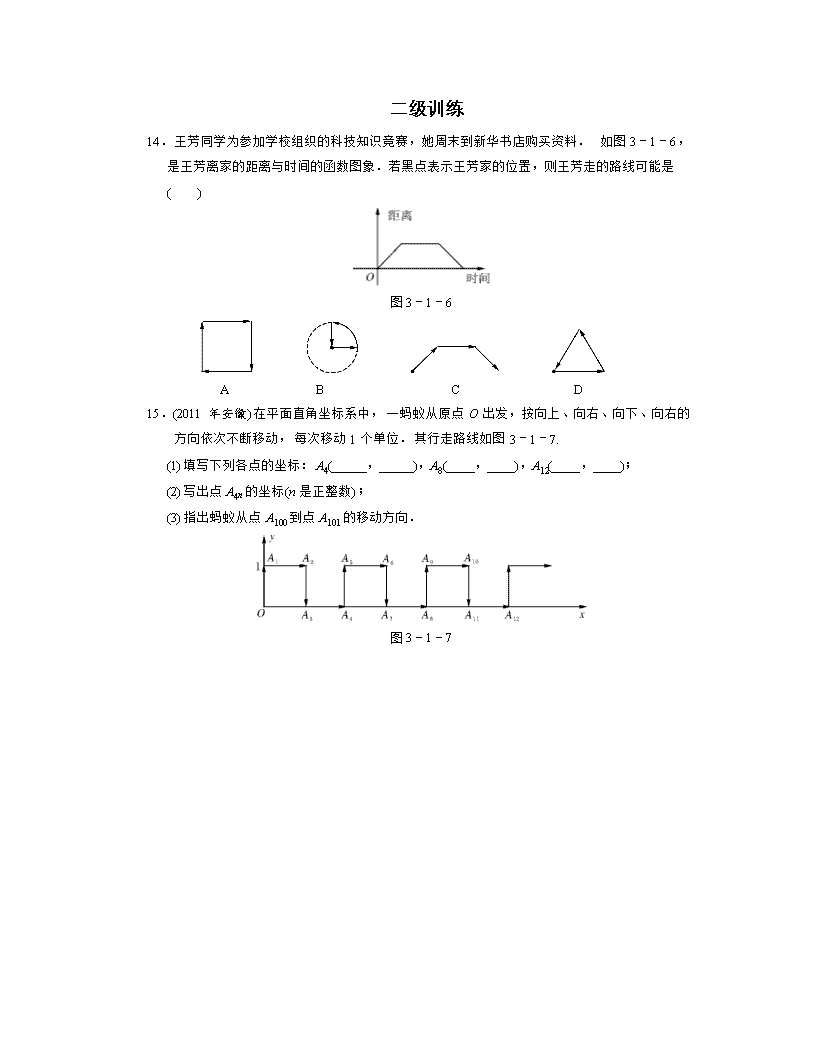
第三章　函数 第1讲　函数与平面直角坐标系 一级训练 ‎1．(2010年广东湛江)点P(1,2)关于x轴的对称点P1的坐标为____________．‎ ‎2．(2012年湖北咸宁)在函数y＝中，自变量x的取值范围是__________．‎ ‎3．(2012年广西玉林)在平面直角坐标系中，一青蛙从点A(－1,0)处向右跳2个单位长度，再向上跳2个单位长度到点A′处，则点A′的坐标为________．‎ ‎4．(2012年山东荷泽)点(－2,1)在平面直角坐标系中所在的象限是(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎5．(2012年山东东营)将点A(2,1)向左平移2个单位长度得到点A′，则点A′的坐标是(　　)‎ A．(2,3) B．(2，－1) C．(4,1) D. (0,1)‎ ‎6．(2010年广东河源)函数 y＝的自变量x的取值范围是(　　)‎ A．x＞1 B．x≤－‎1 ‎‎ C．x≥－1 D．x＞－1‎ ‎7．(2011年山东枣庄)在平面直角坐标系中，点P(－2，x2＋1)所在的象限是(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎8．如图3－1－3，若在象棋棋盘上建立平面直角坐标系，使“帥”位于点(－1，－2)，“馬”位于点(2，－2)，则“兵”位于点(　　)‎ A．(－1,1) B．(－2，－1) C．(－3,1) D．(1，－2)‎ ‎ ‎ 图3－1－3 图3－1－4 图3－1－5‎ ‎9．(2011年内蒙古乌兰察布)在平面直角坐标系中，已知线段AB的两个端点分别是A(4，－1)，B(1,1)，将线段AB平移后得到线段A′B′，若点A′的坐标为(－2,2)，则点B′的坐标为(　　)‎ A．(－5,4) B．(4,3) C．(－1，－2) D．(－2，－1) ‎ ‎10．(2011年湖南衡阳)如图3－1－4，在平面直角坐标系中，菱形MNPO的顶点P坐标是(3,4)，则顶点M，N的坐标分别是(　　)‎ A．M(5,0)，N(8,4) B．M(4,0)，N(8,4) C．M(5,0)，N(7,4) D．M(4,0)，N(7,4)‎ ‎11．(2012年山东潍坊)甲、乙两位同学用围棋子做游戏，如图3－1－5，现轮到黑棋下子，黑棋下一子后白棋下一子，使黑棋的5个棋子组成轴对称图形，白棋的5个棋子也成轴对称图形，则下列下子方法不正确的是(　　)‎ 说明：棋子的位置用数对表示，如A点在(6,3)．‎ A．黑(3,7)，白(5,3) B．黑(4,7)，白(6,2) C．黑(2,7)，白(5,3) D．黑(3,7)，白(2,6)‎ ‎12．(2012年江西)某人驾车从A地上高速公路前往B地，中途在服务区休息了一段时间．出发时油箱中存油‎40升，到B地后发现油箱中还剩油‎4升，则出发后到B地油箱中所剩油y(单位：升)与时间t(单位：小时)之间函数的大致图象是(　　)‎ ‎13．(2010年广东梅州)在平面直角坐标系中，点M的坐标为(a,1－‎2a)．‎ ‎(1)当a＝－1时，点M在坐标系的第________象限(直接填写答案)；‎ ‎(2)将点M向左平移2个单位长度，再向上平移1个单位长度后得到点N.当点N在第三象限时，求a的取值范围．‎ 二级训练 ‎14．王芳同学为参加学校组织的科技知识竞赛，她周末到新华书店购买资料．如图3－1－6，是王芳离家的距离与时间的函数图象．若黑点表示王芳家的位置，则王芳走的路线可能是(　　)‎ 图3－1－6‎ ‎　　　　　　　　　　　　　　　　‎ ‎ 　　 A 　　 B 　　　　 C 　 D ‎15．(2011年安徽)在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图3－1－7.‎ ‎(1)填写下列各点的坐标：A4(_____，_____)，A8(____，____)，A12(____，____)；‎ ‎(2)写出点A4n的坐标(n是正整数)；‎ ‎(3)指出蚂蚁从点A100到点A101的移动方向．‎ 图3－1－7‎ ‎16．(2012年山东泰安)如图3－1－8，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序按图中“→”方向排列，如(1,0)，(2,0)，(2,1)，(1,1)，(1,2)，(2,2)……根据这个规律，第2 012个点的横坐标为________．‎ 图3－1－8‎ 三级训练 ‎17．(2012年广东梅州)如图3－1－9，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A，B的坐标分别是A(3,2)，B(1,3)．△AOB绕点O逆时针旋转90°后得到△A1OB1(直接填写答案)．‎ ‎(1)点A关于点O中心对称的点的坐标为________；‎ ‎(2)点A1的坐标为________；‎ ‎(3)在旋转过程中，点B经过的路径为弧BB1，那么弧BB1的长为________．‎ 图3－1－9‎ ‎18．(2011年贵州贵阳)‎ ‎【阅读】‎ 在平面直角坐标系中，以任意两点P(x1，y1)，Q(x2，y2)为端点的线段的中点坐标为.‎ ‎【运用】‎ ‎(1)如图3－1－10，矩形ONEF的对角线交于点M，ON、OF分别在x轴、y轴上，O为坐标原点，点E的坐标为(4,3)，则点M的坐标为________________；‎ ‎(2)在平面直角坐标系中，有A(－1,2)，B(3,1)，C(1,4)三点，另有一点D与点A，B，C构成平行四边形的顶点，求点D的坐标．‎ 图3－1－10‎ 参考答案 ‎1．(1，－2)　2.x≠3　3.(1,2)　4.B　5.D ‎6．D　7.B　8.C　9.A　10.A ‎11．C　解析：本题可以一个一个选项的判断，哪个位置可以构成轴对称图形．在各个位置补上棋子，观察图形得到选项选项A，B，D都可以构成轴对称图形．故不正确的选项是选项C.‎ ‎ ‎ ‎ 　 　 ‎ ‎ ‎ ‎ 　 　 ‎12．C　解析：选项A，B中，在服务区休息的这段时间，油箱中所剩油在减少，不符合实际意义．选项D中，从服务区到B地，油箱中所剩油在逐渐增加，不符合实际意义．故选C.‎ ‎13．解：(1)由a＝－1，得1－‎2a＝3，‎ ‎∴M在第二象限．‎ ‎(2)平移后点N的坐标为(a－2,2－‎2a)，‎ 又点N在第三象限，∴解得1＜a＜2.‎ ‎14．B ‎15．(1)A4(2,0)　A8(4,0)　A12(6,0)‎ ‎(2)A4n(2n,0)　(3)向上 ‎16. 45　解析：观察图象可知，到每一横坐标相同的点结束，点的总个数等于最后点的横坐标的平方，并且横坐标是奇数时最后以横坐标为该数，纵坐标为0结束，当横坐标是偶数时，以横坐标为1，纵坐标为横坐标减1的点结束，根据此规律解答即可．如：横坐标为1的点结束，共有1个，1＝12，横坐标为2的点结束，共有2个，4＝22，横坐标为3的点结束，共有9个，9＝32，横坐标为4的点结束，共有16个，16＝42，…，横坐标为n的点结束，共有n2个，∵452＝2 025，∴第2 025个点是(45,0)，第2 012个点是(45,13)，所以，第2012个点的横坐标为45.‎ ‎17．(1)(－3，－2)　(2)(－2,3)　(3)π 解析：(3)先利用勾股定理求出OB的长度，然后根据弧长公式计算即可．根据勾股定理，得OB＝＝，∴弧BB1的长＝＝π.‎ ‎18．解：(1)∵四边形ONEF是矩形，‎ ‎∴点M是OE的中点．‎ ‎∵O(0,0)，E(4,3)，‎ ‎∴点M的坐标为.‎ ‎(2)设点D的坐标为(x，y)．‎ 若以AB为对角线，AC，BC为邻边构成平行四边形，则AB，CD的中点重合，‎ ‎∴解得 若以BC为对角线，AB，AC为邻边构成平行四边形，则AD，BC的中点重合，‎ ‎∴解得 若以AC为对角线，AB，BC为邻边构成平行四边形，则BD，AC的中点重合，‎ ‎∴解得 综上可知，点D的坐标为(1，－1)或(5,3)或(－3,5)．‎