上海中考数学二模杨浦卷含答案

上海中考数学二模杨浦卷含答案

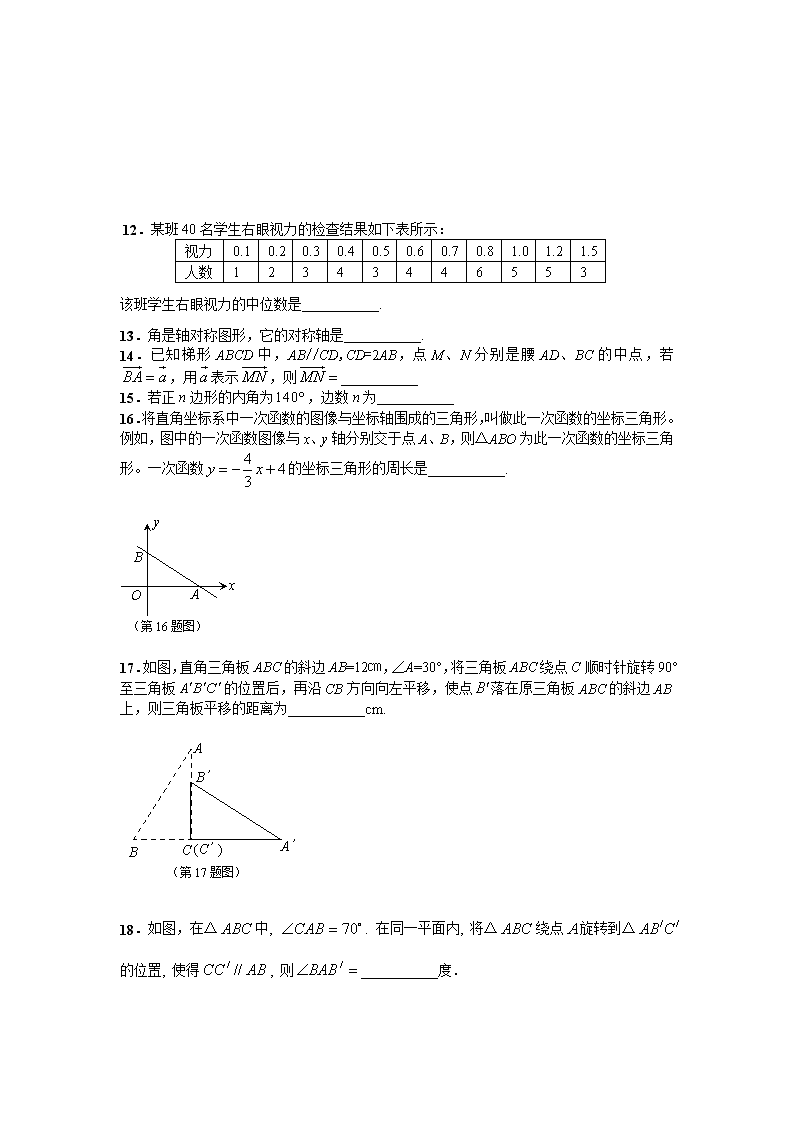
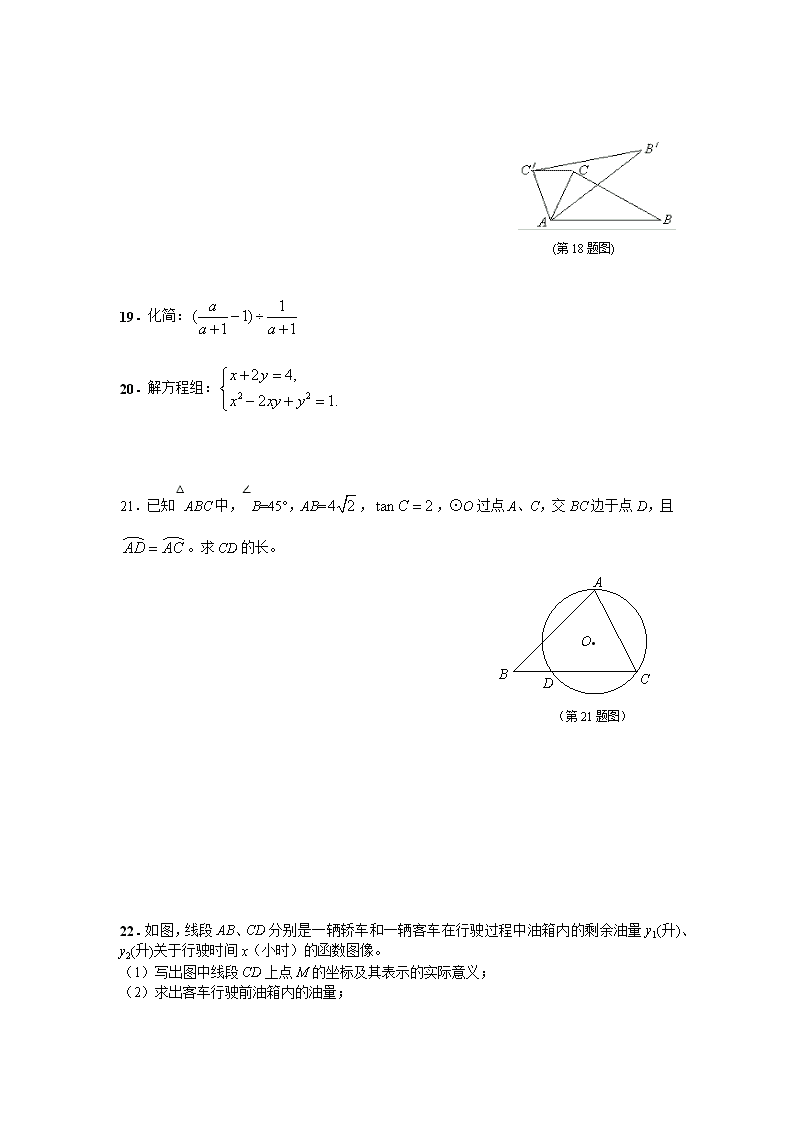
杨浦区初三数学基础测试卷 ‎ ‎1．下列数中能同时被2、3整除的是 （ ）‎ ‎ （A）1.2 ； （B）15 ； （C）16 ； （D）18．‎ ‎2． 下列式子：①，②，③，④，其中属于代数式的是 （ ）‎ ‎ （A）①③； （B）②④； （C）①③④； （D）①②③④．‎ ‎3．用配方法解一元二次方程时，此方程可变形为 （ ）‎ ‎ （A）； （B）； （C）； （D）．‎ 4． 某初级中学要了解全校学生的课外作业负担情况，你认为以下抽样方法中比较合理的是 ‎ （ ）‎ （A） 调查全体女生； （B）调查全体男生； ‎ ‎ （C）调查九年级全体学生； （D）调查六、七、八、九年级各20名学生．‎ ‎5．⊙O的半径为R，直线与⊙O有公共点，如果圆心到直线的距离为d，那么d与R的大小关系是 （ ）‎ ‎（A）； （B）； （C）； （D）．‎ ‎6．下列条件，不能判定与相似的是 （ ）‎ ‎（A） ， ， ； ‎ ‎（B） ，，，，；‎ ‎（C） ，；‎ ‎（D） ，.‎ ‎7．当时，化简：___________.‎ ‎8．因式分解：a3﹣4a=___________. ‎ ‎9．在平面直角坐标系中，若点在第二象限，则的取值范围为___________ ‎ ‎10．函数中，自变量x的取值范围是___________.‎ ‎11． 有一个质地均匀的正方体，其六个面上分别画着圆、等腰三角形、等腰梯形、平行四边形、菱形、正五边形。投掷该正方体一次，向上的一面的图形既是轴对称又是中心对称的概率是___________. ‎ ‎12．某班40名学生右眼视力的检查结果如下表所示：‎ 视力 ‎0.1‎ ‎0.2‎ ‎0.3‎ ‎0.4‎ ‎0.5‎ ‎0.6‎ ‎0.7‎ ‎0.8‎ ‎1.0‎ ‎1.2‎ ‎1.5‎ 人数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎3‎ ‎4‎ ‎4‎ ‎6‎ ‎5‎ ‎5‎ ‎3‎ 该班学生右眼视力的中位数是___________. ‎ ‎13．角是轴对称图形，它的对称轴是___________.‎ ‎14．已知梯形ABCD中，AB//CD,CD=2AB，点M、N分别是腰AD、BC的中点，若，用表示，则___________ ‎ ‎15．若正n边形的内角为，边数n为___________‎ ‎16．将直角坐标系中一次函数的图像与坐标轴围成的三角形，叫做此一次函数的坐标三角形。例如，图中的一次函数图像与x、y轴分别交于点A、B，则△ABO为此一次函数的坐标三角 形。一次函数的坐标三角形的周长是___________.‎ x y O A B ‎（第16题图）‎ ‎17．如图，直角三角板ABC的斜边AB=12㎝，∠A=30°，将三角板ABC绕点C顺时针旋转90°至三角板的位置后，再沿CB方向向左平移，使点落在原三角板ABC的斜边AB上，则三角板平移的距离为___________cm.‎ A B C A’‎ B’‎ ‎(C’)‎ ‎（第17题图）‎ ‎18．如图，在△中, . 在同一平面内, 将△绕点旋转到△的位置, 使得, 则___________度．‎ ‎ (第18题图)‎ ‎19．化简：‎ ‎20．解方程组：‎ 21． 已知△ABC中，∠B=45°，AB=，，⊙O过点A、C，交BC边于点D，且。求CD的长。‎ A ‎.‎ O B C D ‎（第21题图）‎ ‎22．如图，线段AB、CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x（小时）的函数图像。‎ ‎（1）写出图中线段CD上点M的坐标及其表示的实际意义；‎ ‎（2）求出客车行驶前油箱内的油量；‎ ‎（3）求客车行驶1小时所消耗的油量相当于轿车行驶几小时所消耗的油量。‎ y(升)‎ x(小时)‎ ‎60‎ ‎3‎ ‎4‎ y2‎ y1‎ A B C D ‎0‎ M ‎1‎ ‎（第22题图）‎ ‎23．如图，在梯形ABCD中，AD∥BC，AB=AD，∠BAD的平分线AE交BC于点E，联结DE．‎ ‎（1）求证：四边形ABED是菱形；‎ ‎（2）若∠ABC=60°，CE=2BE，试判断△CDE的形状，并说明理由． ‎ ‎（第23题图）‎ ‎24．将抛物线平移，平移后的抛物线与x轴交于点A（-1，0）和点B（3，0），与y轴交于点C，顶点为D。‎ （1） 求平移后的抛物线的表达式和点D的坐标；‎ （2） ‎∠ACB与∠ABD是否相等？请证明你的结论；‎ （3） 点P在平移后的抛物线的对称轴上，且△CDP与△ABC相似，求点P的坐标。‎ ‎（第24题图）‎ ‎25．（本题满分14分，第(1)小题4分，第(2)小题5分，第（3）小题5分）‎ 如图1，已知⊙O的半径长为3，点A是⊙O上一定点，点P为⊙O上不同于点A的动点。‎ ‎（1）当时，求AP的长；‎ ‎（2）如果⊙Q过点P、O，且点Q在直线AP上（如图2），设AP=x，QP=y，求y关于x的函数关系式，并写出函数的定义域；‎ ‎（3）在（2）的条件下，当时（如图3），存在⊙M与⊙O相内切，同时与⊙Q相外切，且OM⊥OQ，试求⊙M的半径的长。‎ ‎（图1）‎ ‎（图2）‎ ‎（图3）‎ ‎（第25题图）‎ ‎2013年杨浦区初三基础测试数学试卷答案及评分标准 ‎1．D；2.B；3.C；4.D；5.B；6.D ‎7．-x-2；8．；9．； 10．；11．；12．0.7 ‎ ‎13．角平分线所在的直线；14．；15．9；16．12；17．；18． ‎ ‎19、解: 原式=----------------------------------------------------4分 ‎ = ------------------------------------------------------------2分 ‎ = ---------------------------------------------------------------2分 ‎=. -------------------------------------------------------------------2分 ‎20、解： 由（2）式得到：，----------------------------------------------1分 ‎ 再得到 或者，------------------------------------1分 ‎ 与（1）式组成方程组：或----------------3分 ‎ 解得：，---------------------------------------------------4分 ‎ 经检验，原方程组的解是：，----------------------------1分 ‎21、解：联结AO，并延长交BC于点H，---------------------------------------------1分 ‎ ∵，∴AH⊥DC，且CD=2CH-----------------------------------------4分 ‎∵AH⊥BC，∠B=45°，AB=，∴AH=4，----------------------------------2分 ‎∵AH⊥BC，，∴CH=2，------------------------------------------------2分 ‎∴CD=4-------------------------------------------------------------------------------------1分 ‎22、解：（1）M（1，60），表示：客车行驶1小时时油箱里的剩余油量为‎60升。2分，2分 ‎（2）设y2=kx+b，则，解得：，y2=-30x+90，-------------2分 ‎ ∵当x=0时，y=90，∴客车行驶前油箱内的油量为‎90升。------------------1分 ‎（3）可求得y1与x的函数关系式是y1= -15x+60，‎ 设客车行驶1小时所消耗的油量相当于轿车行驶x小时所消耗的油量，‎ 据题意得：-----------------------------------------1分 ‎ 解得：x=2‎ 答：客车行驶1小时所消耗的油量相当于轿车行驶2小时所消耗的油量。-----------2分 ‎23、（1）证明：如图，∵AE平分∠BAD，∴∠1=∠2，‎ ‎∵AB=AD，AE=AE，∴△BAE≌△DAE，∴BE=DE，------------------------------------2分 ‎∵AD∥BC，∴∠2=∠3=∠1，∴AB=BE，-------------------------------------------------2分 ‎∵AB=AD ，∴AB=BE=DE=AD，∴四边形ABED是菱形．-----------------------1分 ‎（2）解：△CDE是直角三角形．-------------------------------------------------------------1分 取EC的中点F，联结DF，∵CE=2BE，∴BE=EF=FC，‎ ‎∵ABED是菱形，∴BE=DE，AB//DE，∴DE=EF=FC，且∠DEF=∠ABC，--------2分 ‎∵∠ABC=60°，∴∠DEF=60°，∴△DEF是等边三角形，∴DF=EF=FC，----------2分 ‎∴∠4=∠5，∠6=∠7，∵∠4+∠5+∠6+∠7=180°，∴∠5+∠6=90°，----------------2分 ‎∴△CDE是直角三角形．‎ ‎6‎ ‎5‎ ‎4‎ ‎7‎ ‎24、解：（1）∵将抛物线平移，‎ ‎∴设平移后的抛物线解析式为-----------------------------------------------1分 ‎∵点A（-1，0）和点B（3，0），∴‎ 解得，∴平移后的抛物线解析式为-------------------------2分 顶点D的坐标是（1，4）--------------------------------------------------------------------------1分 （2） ‎∠ACB=∠ABD--------------------------------------------------------------------------------1分 证明：联结CD，∵联结CD，‎ 在△CBD中，∵C（0，3），∴CD=，CB=，BD=,‎ 在△AOC中，AO=1，CO=3，AC=，‎ ‎∴，∴，‎ ‎∴△AOC∽△DCB，∴∠ACO=∠DBC，------------------------------------------------------------2分 ‎∵C(0,3)，B（3，0），∴OB=OC，∴∠OCB=∠OBC=，--------------------------------1分 ‎∴∠ACO+∠OCB=∠DBC+∠OBC，即∠ACB=∠ABD （3） 设对称轴与x轴交于点H，∵C（0，3），D（1，4），∴∠CDH=，‎ ‎∵△ABC中，∠ABC=，又∵△CDP与△ABC相似，‎ ‎∴点P在射线DH上，且∠CDP=∠ABC，∴，----------2分 即，∴，‎ ‎∴----------------------------------------------------------------------------2分 ‎25、解：（1）作OH⊥AP于H，‎ ‎∵OH过圆心，AP是弦，∴AP=2AH，-----------------------------------------------------1分 在Rt△AOH中，∵，OA=3，∴设OH=k，AH=2k，‎ 由得，---------------------------------------------------1分 ‎∴AP=2AH=----------------------------------------------------------------------------2分 ‎（2）联结PO，联结OQ ‎∵⊙Q过点P、O，∴PQ=OQ，∴∠QPO=∠QOP， ‎ ‎∵⊙O过点P、A，∴PO=AO，∴∠QPO =∠A， ‎ ‎∴∠QOP =∠A，又∵∠P=∠P，∴△QPO∽△OPA，------------------------------2分 ‎∴，即，∴，，-------------------------------2分，1分 ‎（3）作PF⊥AO于F，联结OP，设⊙M的半径长为r ‎∵，∴设PF=‎4a，AF=‎3a，a>0，∴OF=3‎-3a，‎ 在Rt△OPF中，∵，即，‎ ‎∴，∴，----------------------------------------------------------1分 即，∴，-----------------------------------------------1分 ‎∵⊙M同时与⊙O相内切，与⊙Q相外切，‎ ‎∴MO=3-r，QM=，-------------------------------------------------------------------1分 ‎∵OM⊥OQ，∴在Rt△OMQ中，，‎ 即，∴，即⊙M的半径长为------------------2分 ‎ ‎