中考数学复习教案时平移旋转技巧归纳

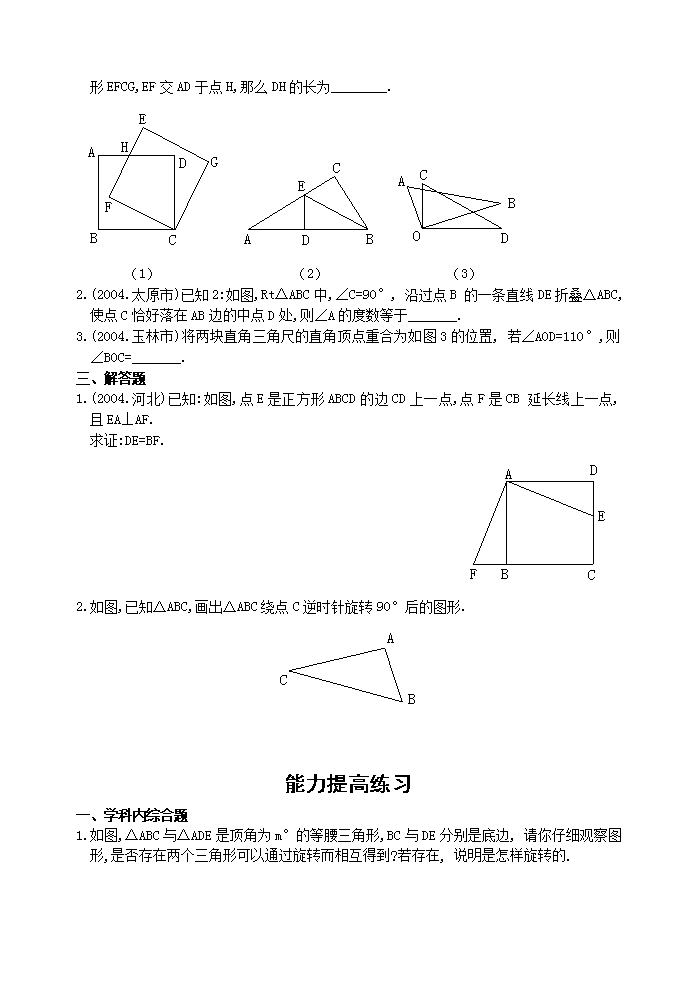
中考数学复习教案时平移旋转技巧归纳

A thesis submitted to XXX in partial fulfillment of the requirement for the degree of Master of Engineering 中考数学复习教案 第24课时 平移、旋转 一、知识点导航图:‎ 二、中考课标要求 ‎ ‎ 考点 课标要求 知识与技能目标 了解 理解 掌握 灵活应用 平移 平移的特征 ‎∨‎ ‎∨‎ ‎∨‎ 画平移后的图形 ‎∨‎ ‎∨‎ 旋转 旋转的特征 ‎∨‎ ‎∨‎ ‎∨‎ 旋转对称图形 ‎∨‎ ‎∨‎ ‎∨‎ 三、中考知识梳理 ‎ 掌握这部分内容,首先弄明白平移,旋转的特征,及平移、旋转的决定因素,明确什么样的图形是旋转对称图形.‎ 四、中考题型例析 ‎1．平移作图 例1 如图,△ABC的边AB平移到了EF,作出平移后的图形即△EFG, 你能给出几种作法?‎ 分析:根据平移的特征:(1)连结对应点的线段平行且相等;(2) 对应线段平行且相等等,可得到两种不同的作法.‎ 方法1:连结AE、BF,过点C作CG∥AE,且使CG=AE,连结EG,FG.‎ 则△EFG就是所要作的三角形.‎ 方法2:过点E作EG∥AC,且EG=AC,连结FG.‎ 则△EFG就是所要作的三角形.‎ 点评:平移作图,往往根据平移的特征来进行.因此,掌握好平移的特征是很重要的.‎ ‎2．旋转的运用 例2 如图,△ABC和△ADE都是等腰直角三角形,∠C和∠AED都是直角,点C在AD上,如果△ABC经旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?‎ 分析:根据旋转的特征,可得出结论. ‎ 解:点A是旋转中心,顺时针方向旋转了45°.‎ 基础达标验收卷 一、选择题 ‎1.如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF ∥BC, 平移△AEF可以得到的三角形是( ) ‎ A.△BDF B.△DEF C.△CDE D.△BDF和△CDE ‎2.一个图形经过平移变换后,有以下几种说法,其中不适当的说法是( )‎ A.平移后,图形的形状和大小都不改变 B.平移后的图形与原图形的对应线段、对应角都相等 C.平移后的图形形状不变,但大小可以改变 D.利用基本图形的平移可以设计美丽的图案 二、填空题 ‎1.(2004.上海)如图1,边长为3的正方形ABCD绕点C按顺时针方向旋转30 °‎ 后得到正方形EFCG,EF交AD于点H,那么DH的长为________.‎ ‎ （1） （2） （3）‎ ‎2.(2004.太原市)已知2:如图,Rt△ABC中,∠C=90°, 沿过点B 的一条直线DE折叠△ABC,使点C恰好落在AB边的中点D处,则∠A的度数等于_______.‎ ‎3.(2004.玉林市)将两块直角三角尺的直角顶点重合为如图3的位置, 若∠AOD=110°,则∠BOC=_______.‎ 三、解答题 ‎1.(2004.河北)已知:如图,点E是正方形ABCD的边CD上一点,点F是CB 延长线上一点,且EA⊥AF.‎ 求证:DE=BF.‎ ‎2.如图,已知△ABC,画出△ABC绕点C逆时针旋转90°后的图形.‎ 能力提高练习 一、学科内综合题 ‎1.如图,△ABC与△ADE是顶角为m°的等腰三角形,BC与DE分别是底边, 请你仔细观察图形,是否存在两个三角形可以通过旋转而相互得到?若存在, 说明是怎样旋转的.‎ 二、开放探索题 ‎2.如图,长方形ABCD经过多次不同方向不同距离的平移后,能否变形A ′B′C′D′的位置?说明理由.‎ 答案：‎ 基础达标验收卷 一、1.D 2.C 二、1. 2.30° 3.70°‎ 三、1.证明:∵四边形ABCD是正方形,‎ ‎∴AB=AD,∠BAD=∠ADE=∠ABF=90°.‎ 又∵EA⊥AF,‎ ‎∴∠BAF+∠BAE=∠BAE+∠DAE=90°.‎ ‎∴∠BAF=∠DAE.‎ ‎∴Rt△ABF≌Rt△ADE.‎ ‎∴DE=BF.‎ 说明:本题也可用旋转的特征来说明.‎ ‎2.略.‎ 能力提高练习 ‎1.解:△ABD与△ACE可以通过旋转相互得到,将△ABD绕点A逆时针旋转m °得到△ACE;也可将△ACE顺时针旋转m°得到△ABD.‎ ‎2.不能.因为对应线段不平行,不满足平移的特征.‎