上海中考数学压轴题解题策略学生版

上海中考数学压轴题解题策略学生版

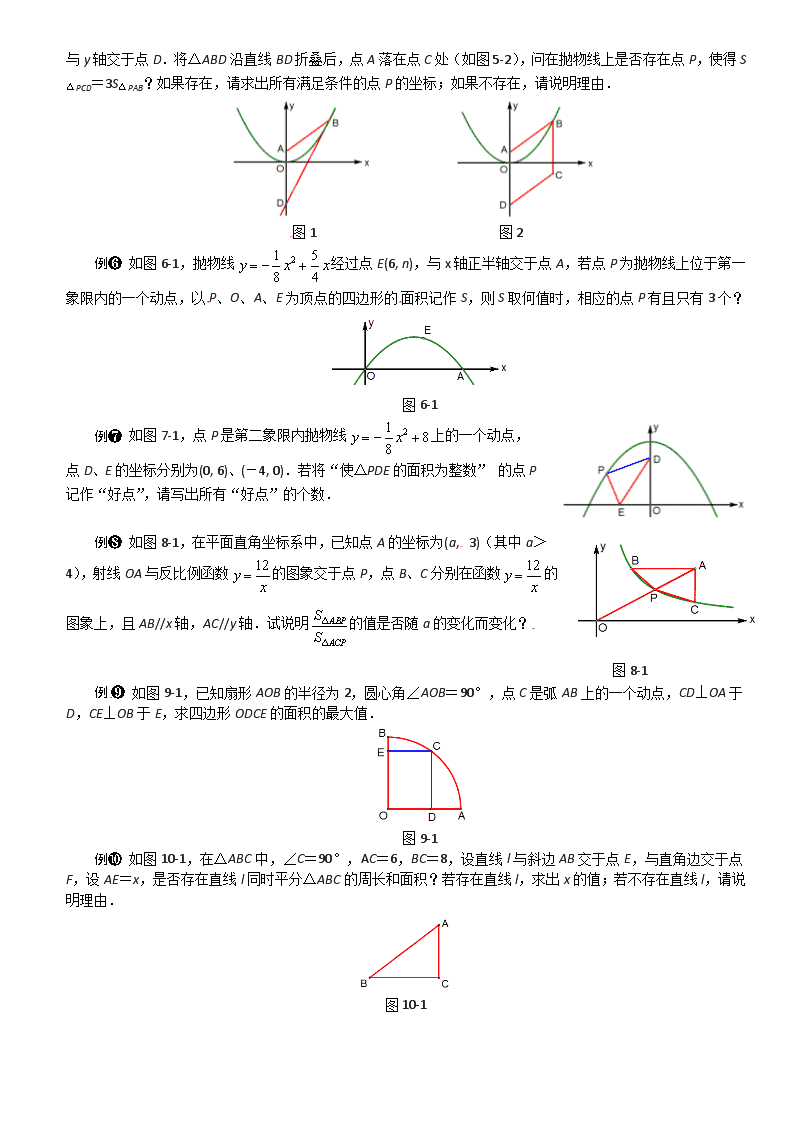
上海中考数学压轴题解题策略 宝龙教育中心整理(2017.3)‎ 一、面积的存在性问题解题策略 专题攻略 面积的存在性问题常见的题型和解题策略有两类：‎ 第一类，先根据几何法确定存在性，再列方程求解，后检验方程的根．‎ 第二类，先假设关系存在，再列方程，后根据方程的解验证假设是否正确．‎ 例题解析 例❶ 如图1-1，矩形ABCD的顶点C在y轴右侧沿抛物线y＝x2－6x＋10滑动，在滑动过程中CD//x轴，CD＝1，AB在CD的下方．当点D在y轴上时，AB落在x轴上．当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时，求点C的坐标．‎ 图1-1‎ 例❷ 如图2-1，二次函数y＝(x＋m)2＋k的图象与x轴交于A、B两点，顶点M的坐标为(1,－4)，AM与y轴相交于点C，在抛物线上是否还存在点P，使得S△PMB=S△BCM，如存在，求出点P的坐标．‎ ‎ ‎ ‎ 图2-1‎ 例❸ 如图3-1，直线y＝x＋1与抛物线y＝－x2＋2x＋3交于A、B两点，点P是直线AB上方抛物线上的一点，四边形PAQB是平行四边形，当四边形PAQB的面积最大时，求点P的坐标．‎ 图3-1 ‎ 例❹ 如图4-1，在平行四边形ABCD中，AB＝3，BC＝5，AC⊥AB，△ACD沿AC方向匀速平移得到△PNM，速度为每秒1个单位长度；同时点Q从点C出发，沿CB方向匀速移动，速度为每秒1个单位长度；当△PNM停止运动时，点Q也停止运动，如图4-2，设移动时间为t秒（0＜t＜4）．是否存在某一时刻t，使S△QMC∶S四边形ABQP＝1∶4？若存在，求出t的值；若不存在，请说明理由．‎ 图4-1 图4-2‎ 例❺ 如图5-1，在平面直角坐标系中，点A的坐标为(0, 1)，直线y＝2x－4与抛物线相交于点B ‎，与y轴交于点D．将△ABD沿直线BD折叠后，点A落在点C处（如图5-2），问在抛物线上是否存在点P，使得S△PCD＝3S△PAB？如果存在，请求出所有满足条件的点P的坐标；如果不存在，请说明理由．‎ 图1 图2‎ 例❻ 如图6-1，抛物线经过点E(6, n)，与x轴正半轴交于点A，若点P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形的面积记作S，则S取何值时，相应的点P有且只有3个？‎ 图6-1‎ 例❼ 如图7-1，点P是第二象限内抛物线上的一个动点，点D、E的坐标分别为(0, 6)、(－4, 0)．若将“使△PDE的面积为整数” 的点P记作“好点”，请写出所有“好点”的个数．‎ 例❽ 如图8-1，在平面直角坐标系中，已知点A的坐标为(a, 3)（其中a＞4），射线OA与反比例函数的图象交于点P，点B、C分别在函数的图象上，且AB//x轴，AC//y轴．试说明的值是否随a的变化而变化？‎ ‎ 图8-1‎ 例❾ 如图9-1，已知扇形AOB的半径为2，圆心角∠AOB＝90°，点C是弧AB上的一个动点，CD⊥OA于D，CE⊥OB于E，求四边形ODCE的面积的最大值．‎ 图9-1‎ 例❿ 如图10-1，在△ABC中，∠C＝90°，AC＝6，BC＝8，设直线l与斜边AB交于点E，与直角边交于点F，设AE＝x，是否存在直线l同时平分△ABC的周长和面积？若存在直线l，求出x的值；若不存在直线l，请说明理由．‎ 图10-1‎ 二、平行四边形的存在性问题解题策略 专题攻略 解平行四边形的存在性问题一般分三步：‎ 第一步寻找分类标准，第二步画图，第三步计算．‎ 难点在于寻找分类标准，分类标准寻找的恰当，可以使解的个数不重复不遗漏，也可以使计算又好又快．‎ 如果已知三个定点，探寻平行四边形的第四个顶点，符合条件的有3个点：以已知三个定点为三角形的顶点，过每个点画对边的平行线，三条直线两两相交，产生3个交点．‎ 如果已知两个定点，一般是把确定的一条线段按照边或对角线分为两种情况．‎ 根据平行四边形的对边平行且相等，灵活运用坐标平移，可以使得计算过程简便．‎ 根据平行四边形的中心对称的性质，灵活运用坐标对称，可以使得解题简便．‎ 例题解析 例❶ 如图1-1，在平面直角坐标系中，已知抛物线y＝－x2－2x＋3与x轴交于A、B两点（A在B的左侧），与y轴交于点C，顶点为P，如果以点P、A、C、D为顶点的四边形是平行四边形，求点D的坐标．‎ ‎ 图1-1‎ 例❷ 如图2-1，在平面直角坐标系中，已知抛物线y＝－x2+2x＋3与x轴交于A、B两点，点M在这条抛物线上，点P在y轴上，如果以点P、M、A、B为顶点的四边形是平行四边形，求点M的坐标．‎ 图2-1‎ 例❸ 如图3-1，在平面直角坐标系中，直线y＝－x＋4与x轴交于点A，与y轴交于点B，点C在直线AB上，在平面直角坐标系中求一点D，使得以O、A、C、D为顶点的四边形是菱形．‎ 图 3-1‎ 例❹ 如图4-1，已知抛物线与x轴的负半轴交于点C，点E的坐标为(0,－3)，点N在抛物线的对称轴上，点M在抛物线上，是否存在这样的点M、N，使得以M、N、C、E为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由．‎ ‎ 图4-1‎ 例❺如图1，在平面直角坐标系中，抛物线y＝ax2－2ax－‎3a（a＜0）与x轴交于A、B两点（点A在点B的左侧），点D是第四象限内抛物线上的一点，直线AD与y轴负半轴交于点C，且CD＝‎4AC．设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否成为矩形？若能，求出点P 的坐标；若不能，请说明理由．‎ 图5-1‎ 例❻ 如图6-1，将抛物线c1：沿x轴翻折，得到抛物线c2．‎ 现将抛物线c1向左平移m个单位长度，平移后得到新抛物线的顶点为M，与x轴的交点从左到右依次为A、B；将抛物线c2向右也平移m个单位长度，平移后得到新抛物线的顶点为N，与x轴的交点从左到右依次为D、E．在平移过程中，是否存在以点A、N、E、M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由．‎ 图6-1‎ 例❼ 如图7-1，菱形ABCD的边长为4，∠B＝60°，E、H分别是AB、CD的中点，E、G分别在AD、BC上，且AE＝CG．‎ ‎（1）求证四边形EFGH是平行四边形；‎ ‎（2）当四边形EFGH是矩形时，求AE的长；‎ ‎（3）当四边形EFGH是菱形时，求AE的长．‎ ‎ 图7-1‎ 例❽ 如图8-1，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A(4, 0)、B(0, 3)，点C的坐标为(0, m)，过点C作CE⊥AB于点E，点D为x轴正半轴的一动点，且满足OD＝2OC，连结DE，以DE、DA为边作平行四边形DEFA．‎ ‎（1）如果平行四边形DEFA为矩形，求m的值；‎ ‎（2）如果平行四边形DEFA为菱形，请直接写出m的值．‎ 图8-1‎ 三、梯形的存在性问题解题策略 专题攻略 解梯形的存在性问题一般分三步：‎ 第一步分类，第二步画图，第三步计算．‎ 一般是已知三角形的三个顶点，在某个图象上求第四个点，使得四个点围成梯形．过三角形的每个顶点画对边的平行线，这条直线与图象的交点就是要探寻的梯形的顶点．‎ 因为梯形有一组对边平行，因此根据同位角或内错角，一定可以构造一组相等的角，然后根据相似比列方程，可以使得解题简便．‎ 例题解析 例❶ 如图1-1，四边形ABCD是直角梯形，AD//BC，∠B＝90°，AD＝‎24cm，BC＝‎28cm．点P从点A出发以‎1cm/s的速度向点D运动；点Q从点C同时出发，以‎3cm/s的速度向点B运动，其中一个动点到达终点时，另一个点也随之停止运动．从运动开始，经过多长时间，四边形PQCD成为平行四边形？成为等腰梯形？‎ 图1-1‎ 例❷ 如图2-1，在Rt△ABC中，∠C＝90°，AC＝3，AB＝5．点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动；同时点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．当点P到达点A时停止运动，点Q也随之停止．伴随着P、Q的运动，DE保持垂直平分PQ，DE交BC于点E．设P、Q运动的时间是t秒（t＞0），在运动的过程中，四边形QBED能否成为直角梯形？若能，求出t的值；若不能，请说明理由．‎ 图2-1‎ 例❸如图，已知A、B是双曲线上的两个点，A、B的横坐标分别为2和－1，BC⊥x轴，垂足为C．在双曲线上是否存在点D，使得以A、B、C、D为顶点的四边形是梯形？如果存在，求出点D的坐标；如果不存在，请说明理由．‎ 图3-1‎ 例❹如图4-1，已知抛物线与x轴的交点为A、D（A在D的右侧），与y轴的交点为C，设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P 为顶点的四边形为梯形？若存在，求出点P的坐标；若不存在，请说明理由．‎ 图4-1‎ 例❺ 如图5-1，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A(1，2)．抛物线y＝ax2＋bx＋c经过O、A、C三点．‎ ‎（1）求该抛物线的函数解析式；‎ ‎（2）点P为线段OC上的一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由． ‎ 图5-1‎ 例❻ 如图6-1，在矩形ABCD中，AB＝3，BC＝4，动点P从点D出发沿DA向终点A运动，同时动点Q从点A出发沿对角线AC向终点C运动．过点P作PE//DC，交AC于点E，动点P、Q的运动速度都是每秒1个单位长度，当点P运动到点A时，P、Q两点同时停止运动，设运动时间为x秒，当x为何值时，四边形PQBE为梯形？‎ 图6-1‎ 四、线段和差最值的存在性问题解题策略 专题攻略 两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图1）．‎ 三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图2）．‎ 两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，PA与PB的差的最大值就是AB，此时点P在AB的延长线上，即P′．‎ 解决线段和差的最值问题，有时候求函数的最值更方便，本讲不涉及函数最值问题．‎ 图1 图2 图3‎ 例题解析 例❶ 如图1-1，抛物线y＝x2－2x－3与x轴交于A、B两点，与y轴交于点C，点P是抛物线对称轴上的一个动点，如果△PAC的周长最小，求点P的坐标．‎ 图1-1‎ 例❷如图，抛物线与y轴交于点A，B是OA的中点．一个动点G从点B出发，先经过x轴上的点M，再经过抛物线对称轴上的点N，然后返回到点A．如果动点G走过的路程最短，请找出点M、N的位置，并求最短路程．‎ 图2-1‎ 例❸ 如图3-1，抛物线与y轴交于点A，顶点为B．点P是x轴上的一个动点，求线段PA与PB中较长的线段减去较短的线段的差的最小值与最大值，并求出相应的点P的坐标．‎ 图3-1‎ 例❹ 如图4-1，菱形ABCD中，AB＝2，∠A＝120°，点P、Q、K分别为线段BC、CD、BD上的任意一点，求PK＋QK的最小值．‎ 图4-1‎ 例❺ 如图5-1，菱形ABCD中，∠A＝60°，AB＝3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙B和⊙A上的动点，求PE＋PF的最小值．‎ 图5-1‎ 例❻ 如图6-1，已知A(0, 2)、B(6, 4)、E(a, 0)、F(a＋1, 0)，求a为何值时，四边形ABEF周长最小？请说明理由．‎ 图6-1‎ 例❼ 如图7-1，△ABC中，∠ACB＝90°，AC＝2，BC＝1．点A、C分别在x轴和y轴的正半轴上，当点A在x轴上运动时，点C也随之在y轴上运动．在整个运动过程中，求点B到原点的最大距离．‎ 图7-1‎ 例❽ 如图8-1，已知A(－2,0)、B(4, 0)、．设F为线段BD上一点（不含端点），连结AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止．当点F的坐标是多少时，点M在整个运动过程中用时最少？‎ 图8-1‎ 例❾ 如图9-1，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8．点E是BC边上的点，连结AE，过点E作AE 的垂线交AB边于点F，求AF的最小值．‎ 图9-1‎ 例❿ 如图10-1，已知点P是抛物线上的一个点，点D、E的坐标分别为(0, 1)、(1, 2)，连结PD、PE，求PD＋PE的最小值．‎ 图10-1‎ 五、相切的存在性问题解题策略 专题攻略 一、圆与圆的位置关系问题，一般无法先画出比较准确的图形．‎ 解这类问题，一般分三步走，第一步先罗列三要素：R、r、d，第二步分类列方程，第三步解方程并验根．‎ 第一步在罗列三要素R、r、d的过程中，确定的要素罗列出来以后，不确定的要素要用含有x的式子表示．第二步分类列方程，就是指外切与内切两种情况．‎ 二、直线与圆的位置关系问题，一般也无法先画出比较准确的图形．‎ 解这类问题，一般也分三步走，第一步先罗列两要素：R和d，第二步列方程，第三步解方程并验根．‎ 第一步在罗列两要素R和d的过程中，确定的要素罗列出来以后，不确定的要素要用含有x的式子表示．第二步列方程，就是根据直线与圆相切时d＝R列方程．‎ 例题解析 例❶ 如图1-1，已知抛物线y＝x2－1与x轴相交于A、B两点．‎ ‎（1）有一半径为r的⊙P，且圆心P在抛物线上运动，当⊙P与两坐标轴都相切时，求半径r的值；‎ ‎（2）半径为1的⊙P在抛物线上，当点P的纵坐标在什么范围内取值时，⊙P与y轴相离、相交？ ‎ ‎ 图1-1 ‎ 例❷ 如图2-1，△ABC中，BC＝AC＝5，AB＝8，CD为AB边上的高．如图2-1，A在原点处，点B在y轴的正半轴上，点C在第一象限．若A从原点出发，沿x轴向右以每秒1个单位长的速度运动，则点B随之沿y轴下滑，并带动△ABC在平面上滑动．如图2-2，设运动的时间为t秒，当B到达原点时停止运动．当以点C为圆心、CA为半径的圆与坐标轴相切时，求t的值．‎ 图2-1 图2-2‎ 例❸ 如图3-1，A(－5,0)，B(－3,0)，C(0, 3)，四边形OADC是矩形．点P从点Q(4,0)出发，沿x轴向左以每秒1个单位长的速度运动，以PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求运动时间t的值．‎ ‎ ‎ ‎ 图3-1‎ 例❹ 如图4-1，已知抛物线y＝mx2＋bx＋c(m＞0)经过A(1, 0)、B(－3,0)两点，顶点为P，与y轴交于点D．⊙C的直径为A、B，当m为何值时，直线PD与⊙C相切？‎ 图4-1‎ 例❺ 如图5-1，在梯形ABCD中，∠ABC＝90°，AD∥BC，AB＝8，BC＝18，，点P从点B开始沿BC边向终点C以每秒3个单位的速度移动，点Q从点D开始沿DA边向终点A以每秒2个单位的速度移动，设运动时间为秒．如果⊙P的半径为6，⊙Q的半径为4，在移动的过程中，试探索：为何值时⊙P与⊙Q外离、外切、相交？‎ 图5-1‎ 例❻ 如图6-1，Rt△ABC中，∠ACB＝90°，AC＝‎4厘米，BC＝‎3厘米，⊙O为△ABC的内切圆．‎ ‎（1）求⊙O的半径；‎ ‎（2）动点P从点B沿BA向点A以每秒‎1厘米的速度匀速运动，以P为圆心，PB为半径作圆．设点P运动的时间为t秒，若⊙P与⊙O相切，求t的值．‎ 图6-1‎ 例❼ 如图7-1，已知直线l：与x轴、y轴分别交于点A、B，⊙O的半径为1，点C是y轴正半轴上的一点，如果⊙C既与⊙O相切，也与直线l相切，求圆心C的坐标．‎ 图7-1‎ 例❽ 如图8-1，已知在等腰△ABC中，AB＝AC＝5，BC＝6，点D为BC边上一动点（不与点B重合），过点D作射线DE交AB于点E，∠BDE＝∠A，以点D为圆心，DC的长为半径作⊙D．设BD＝x．‎ ‎（1）当⊙D与边AB相切时，求x的值； ‎ ‎（2）如果⊙E是以E为圆心，AE的长为半径的圆，当⊙D与⊙E相切时，求x的值． ‎ ‎ 图8-1‎ 例❾ 如图9-1，一个Rt△DEF的直角边DE落在AB上，点D与点B重合，过A点作射线AC与斜边EF平行，已知AB＝12，DE＝4，DF＝3．如图9-2，点P从A点出发，沿射线AC方向以每秒2个单位的速度运动，Q为AP的中点．同时Rt△DEF沿着BA方向以每秒1个单位的速度运动，当点D运动到点A时，两个运动都停止．在运动过程中，是否存在以点Q为圆心的圆与Rt△DEF的两条直角边所在直线都相切？若存在，求运动时间t，若不存在，说明理由．‎ 图9-1 图9-2‎ 六、相似三角形的存在性问题解题策略 专题攻略 相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．‎ 判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验，如例题1、2、3、4．‎ 应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等，如例题6．‎ 应用判定定理3解题不多见，如例题5，根据三边对应成比例列连比式解方程（组）．‎ 例题解析 例❶ 如图1-1，抛物线与x轴交于A、B两点（A点在B点左侧），与y轴交于点C．动直线EF（EF//x轴）从点C开始，以每秒1个单位的速度沿y轴负方向平移，且分别交y轴、线段BC于E、F两点，动点P同时从点B出发，在线段OB上以每秒2个单位的速度向原点O运动．是否存在t，使得△BPF与△ABC 相似．若存在，试求出t的值；若不存在，请说明理由．‎ 图1-1‎ 例❷ 如图2-1，在平面直角坐标系中，顶点为M的抛物线y＝ax2＋bx（a＞0）经过点A和x轴正半轴上的点B，AO＝BO＝2，∠AOB＝120°．‎ ‎（1）求这条抛物线的解析式；‎ ‎（2）连结OM，求∠AOM的大小；‎ ‎（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．‎ ‎ 图2-1 ‎ 例❸ 如图3-1，抛物线y＝ax2＋bx－3与x轴交于A(1, 0)、B(3, 0)两点，与y轴交于点D，顶点为C．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）在x轴下方的抛物线上是否存在点M，过M作MN⊥x轴于点N，使以A、M、N为顶点的三角形与△BCD相似？若存在，求出点M的坐标；若不存在，请说明理由．‎ 图3-1‎ 例❹ 如图4-1，在平面直角坐标系中，A(8,0)，B(0,6)，点C在x轴上，BC平分∠OBA．点P在直线AB上，直线CP与y轴交于点F，如果△ACP与△BPF相似，求直线CP的解析式．‎ 图4-1‎ 例❺ 如图5-1，二次函数y＝x2＋3x的图象经过点A(1,a)，线段AD平行于x轴，交抛物线于点D．在y轴上取一点C(0, 2)，直线AC交抛物线于点B，连结OA、OB、OD、BD．求坐标平面内使△EOD∽△AOB的点E的坐标；‎ 图5-1‎ 例❻ 如图6-1，在△ABC中，AB＝AC＝4，BC＝8．⊙A的半径为2，动点P从点B出发沿BC方向以每秒1个单位的速度向点C运动．延长BA交⊙A于点D，连结AP交⊙A于点E，连结DE并延长交BC于点F．设点P运动的时间为t秒，当△ABP与△FBD相似时，求t的值．‎ 图6-1‎ 七、直角三角形的存在性问题解题策略 专题攻略 解直角三角形的存在性问题，一般分三步走，第一步寻找分类标准，第二步列方程，第三步解方程并验根．‎ 一般情况下，按照直角顶点或者斜边分类，然后按照三角比或勾股定理列方程．‎ 有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．‎ 解直角三角形的问题，常常和相似三角形、三角比的问题联系在一起．‎ 如果直角边与坐标轴不平行，那么过三个顶点作与坐标轴平行的直线，可以构造两个新的相似直角三角形，这样列比例方程比较简便．‎ 在平面直角坐标系中，两点间的距离公式常常用到．‎ 怎样画直角三角形的示意图呢？如果已知直角边，那么过直角边的两个端点画垂线，第三个顶点在垂线上；如果已知斜边，那么以斜边为直径画圆，直角顶点在圆上（不含直径的两个端点）．‎ 例题解析 例❶ 如图1-1，在△ABC中，AB＝AC＝10，cos∠B＝．D、E为线段BC上的两个动点，且DE＝3（E在D右边），运动初始时D和B重合，当E和C重合时运动停止．过E作EF//AC交AB于F，连结DF．设BD＝x，如果△BDF为直角三角形，求x的值．‎ 图1-1‎ 例❷ 如图2-1，已知A、B是线段MN上的两点，，，．以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成 ‎△ABC，设AB＝x，若△ABC为直角三角形，求x的值．‎ 图2-1‎ 例❸ 如图3-1，已知在平面直角坐标系中，点A的坐标为（-2, 0），点B是点A关于原点的对称点，P 是函数图象上的一点，且△ABP是直角三角形，求点P的坐标．‎ 图3-1‎ 例❹ 如图4-1，已知直线y＝kx－6经过点A(1,－4)，与x轴相交于点B．若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标．‎ 图4-1‎ 例❺ 如图5-1，抛物线与x轴交于A、B两点（点A在点B的左侧）．若直线l过点E(4, 0)，M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．‎ 图5-1‎ 例❻ 如图6-1，在△ABC中，CA＝CB，AB＝8，．点D是AB边上的一个动点，点E与点A关于直线CD对称，连结CE、DE．‎ ‎（1）求底边AB上的高；‎ ‎（2）设CE与AB交于点F，当△ACF为直角三角形时，求AD的长；‎ ‎（3）连结AE，当△ADE是直角三角形时，求AD的长．‎ 图6-1‎