中考总复习—全等三角形中辅助线的添加(最经典最全面),有答案

中考总复习—全等三角形中辅助线的添加(最经典最全面),有答案

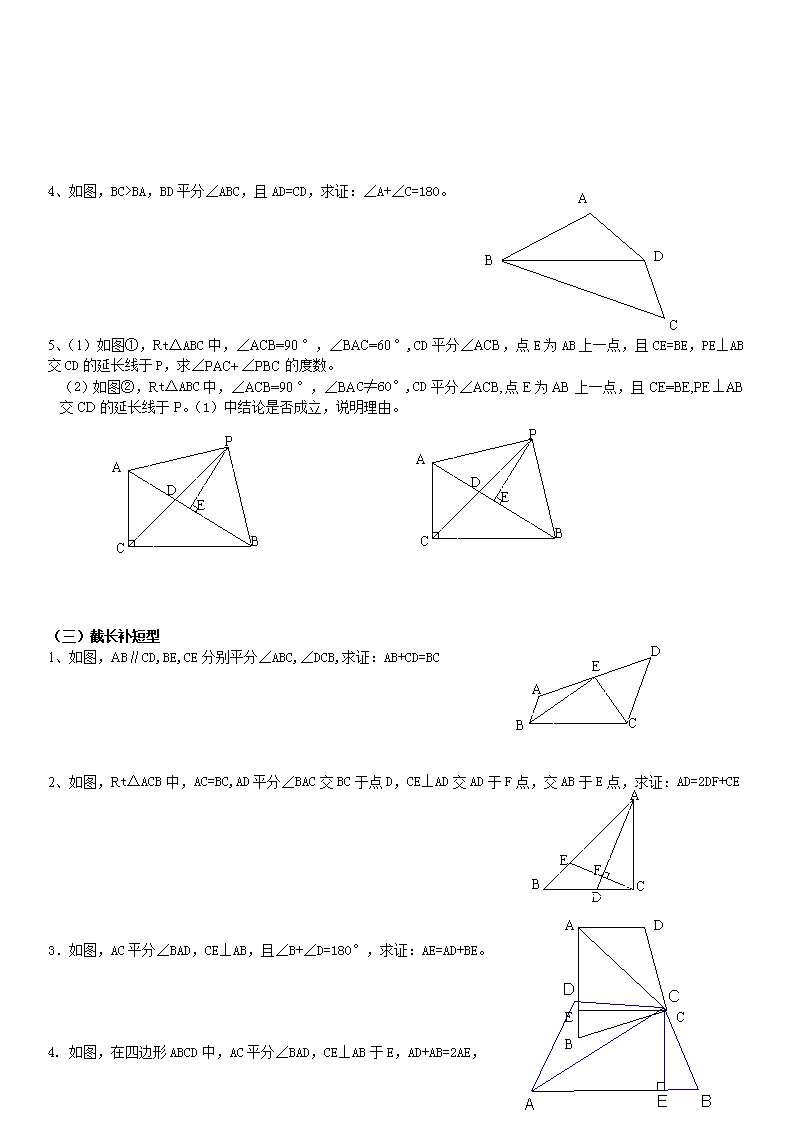
全等三角形及其辅助线作法 常见辅助线的作法有以下几种：‎ 1) 遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”（或构造平行线的X型全等）．‎ 2) 遇到角平分线，一是可以自角平分线上的某一点向角的两边作垂线，二是在角的两边上截取相同的线段，构成全等。利用的思维模式是三角形全等变换中的“对折”，也是运用了角的对称性。 ‎ 3) 截长法与补短法，具体做法是在较长线段上截取一条线段与特定线段相等，使剩下的线段与另一条线段相等；或者是将两条较短线段中的一条延长，使这两条线段的和等于较长的线段。这种作法，适合于证明线段的和、差、倍、分等题目．‎ 4) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”．也可以将两腰分拆到两个三角形中，证明这两个三角形全等。特殊的应用有等边三角形与等腰直角三角形。‎ 5) 此外，还有旋转、折叠等情况。‎ ‎(一)、中点线段倍长问题（中线倍长或者倍长中线）：‎ ‎1、（“希望杯”试题）已知，如图△ABC中，AB=5，AC=3，则中线AD的取值范围是_________.‎ ‎2、如图△ABC中，点D是BC边中点，过点D作直线交AB、CA延长线于点E、F。当AE=AF时，求证BE=CF。‎ A B C D E F ‎3、如图，△ABC中，E、F分别在AB、AC上，DE⊥DF，D是中点，试比较BE+CF与EF的大小.‎ ‎4、如图，△ABC中，BD=DC=AC，E是DC的中点，求证：AD平分∠BAE.‎ ‎5 如图，AB=AC，AD=AE，M为BE中点，∠BAC=∠DAE=90°。求证：AM⊥DC。‎ D M CD ED AD BD 应用：‎ ‎1、以△ABC以的两边AB、AC为腰分别向外作等腰Rt△ABD和等腰Rt△ACE，且∠BAD=∠CAE-90°，连接DE，M、N分别是BC、DE的中点．探究：AM与DE的位置关系及数量关系．‎ ‎（1）如图① 当△ABC为直角三角形时，AM与DE的位置关系是 ，‎ 线段AM与DE的数量关系是 ；‎ ‎（2）将图①中的等腰Rt△ABD绕点A沿逆时针方向旋转θ° (0<θ<90)后，如图②所示，（1）问中得到的两个结论是否发生改变？并说明理由．‎ ‎（二）角平分线与轴对称 ‎1、如图，已知AD为△ABC的角平分线，∠C=2∠B，求证:AB=AC+CD.‎ B C D A 2、 如图，直线l1∥l2，直线m与直线l1 、l2交于A、B两点。AE、BE为其同旁内角平分线，过E点作直线与l1 、l2交于D、C两点，求证AD+BC=AB。‎ l1‎ l2‎ A B C D E m ‎1‎ ‎2‎ A C D B ‎3、如图，AB>AC, ∠1=∠2，求证：AB－AC>BD－CD。‎ B D C A ‎4、如图，BC>BA，BD平分∠ABC，且AD=CD，求证：∠A+∠C=180。‎ ‎5、（1）如图①，Rt△ABC中，∠ACB=90°，∠BAC=60°,CD平分∠ACB，点E为AB上一点，且CE=BE，PE⊥AB交CD的延长线于P，求∠PAC+∠PBC的度数。‎ ‎（2）如图②，Rt△ABC中，∠ACB=90°，∠BAC≠60°,CD平分∠ACB,点E为AB上一点，且CE=BE,PE⊥AB交CD的延长线于P。（1）中结论是否成立，说明理由。‎ A B C D E P A B C D E P A B C D E ‎（三）截长补短型 ‎1、如图，AB∥CD,BE,CE分别平分∠ABC,∠DCB,求证：AB+CD=BC A B C D E F ‎2、如图，Rt△ACB中，AC=BC,AD平分∠BAC交BC于点D，CE⊥AD交AD于F点，交AB于E点，求证：AD=2DF+CE D A E C B ‎3．如图，AC平分∠BAD，CE⊥AB，且∠B+∠D=180°，求证：AE=AD+BE。‎ ‎4. 如图，在四边形ABCD中，AC平分∠BAD，CE⊥AB于E，AD+AB=2AE，‎ 求证： ∠ADC+∠B=180º ‎ D C B A ‎5. 已知：如图，等腰三角形ABC中，AB=AC，A=108°，BD平分ABC。‎ 求证：BC=AB+DC。‎ M B D C A ‎6. 如图，已知Rt△ABC中，∠ACB=90°，AD是∠CAB的平分线，DM⊥AB于M，且AM=MB。求证：CD=DB。‎ ‎ ‎ A B C E O F y x ‎7、如图，直线AB交x轴于A(m,o)，交y轴于B（o,n）,其中m,n满足m2+‎4m+4+ =0.C为B点关于x轴的对称点，当直线OF的解析式y=kx，当k的值发生改变时（但始终保持k＜0）。过C点作CE∥AB交直线于E点，下列两个结论：①的值不变。②的值不变。其中有且只有一个是正确的，请你找出正确的结论并求其值。‎ ‎（四）等腰直角三角形，等边三角形 A B D E C 图 ‎1、 如图，已知BE、CF是△ABC中AC、AB上的高，在射线BE上截取BP=AC，在射线CF上截取CQ=AB，求证：（1）AP=AQ；（2）AP⊥AQ；‎ x A D E P O y ‎②‎ ‎2、如图①OA=2，OB=4，以A点为顶点，AB为腰在第三象限作等腰Rt△ABC。(1)求C点的坐标。‎ x y F G H O ‎③‎ A B C O y x ‎①‎ ‎(2)如图②，P为y轴负半轴上一个动点，当P点向y轴负半轴向下运动时，若以P点为顶点，PA为腰作等腰Rt△APD，过D点作DE⊥x轴于E点，求OP-DE的值。‎ ‎（3）如图③，已知点F坐标为(-4，-4)，当G在y轴的负半轴上沿负方向运动时，作Rt△FGH，始终保持∠GFH=90°，FG与y轴负半轴交于点G(o,m),FH与x轴正半轴交于点H(n,o)，当G点在y轴负半轴沿负方向运动时，求m+n的值。‎ ‎3、如图，△ABC中，AB=AC, ∠A=90°,点D为BC边的中点，E、F分别在AB、BC上，且ED⊥FD，EG⊥BC于G点，FH⊥BC于H点，下列结论：① DE=DF②AE+AF=AB③S四边形AEDF=S△ABC.④EG+FG=BC,其中结论正确的是（ ）‎ A、只有②③. B、只有①④. C、只有①②③. D、只有①②③④.‎ A B C D E F G H A B C D O y x ‎4、如图，在△ACE中，∠ACB=90°‎ ‎,AC=BC,BC与y轴交于D点，点C的坐标为(-1，0).点A的坐标为(-4,2),，则D点坐标为＿＿＿＿＿＿＿＿‎ A B C D E F G H ‎5、如图，G为线段AB上一点，AC⊥AB,BD⊥AB,GE⊥AB,且AC=BG，BD=AG,GE=AB.若∠AEB=50°，求∠CED的度数。‎ ‎（五）旋转、折叠 ‎1、（倍角与半角问题）（1）如图，Rt△ABC中，∠ACB=90°，AC=BC,点D、E在斜边AB上，且∠DCE=45°，求证AD+BE＞DE.‎ A B C D E ‎（2）如图，若将Rt△ABC改为等边三角形，∠DCE=30°,其它条件不变，上述结论成立吗？试证明。‎ A B C D E ‎2、如图,RT△CDA≌RT△CDB,‎ ‎①、若∠ACD=30°，∠MDN=45°,当∠MDN绕点D旋转时，AM、MN、BN三条线段之间的关系式为＿＿＿＿＿＿‎ ‎②、若∠ACD=45°，∠MDN=45°,AM、MN、BN三条线段之间的数量关系式为：＿＿＿＿＿＿‎ ‎③、由①②猜想：在上述条件下，当∠ACD与∠MDN满足什么条件时，上述关系式成立，证明你的结论。‎ A B C D M N ‎③‎ B D A C M N ‎②‎ B A C D M N ‎①‎ ‎ ‎ ‎3、如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．‎ ‎ (1)如图②，若M为AD边的中点，‎ ‎ ①,△AEM的周长=_____cm；‎ ‎②求证：EP=AE+DP；‎ ‎ (2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．‎ 4、 已知三点A(a,b)、B(3,1)、C(6,0)，其中a,b满足(a-2)2=-.‎ ‎（1）求A的坐标。‎ ‎（2）点P为x轴上一动点，当△OAP与△CBP的周长和取得最小值时，求P点坐标；‎ ‎（3）点P为x轴上一动点，当∠APB=20°时，求∠OAP+∠PBC的度数。‎ y O B C x 4、 已知△ABC中，∠BAC=45°,以AB,AC为边在△ABC外作等腰△ABD和△ACE，AB=AD，AC=AE，且∠BAD=∠CAE，连接CD,BE并交于F点，连接AF。‎ A B C D E F （1） 如图①，若∠BAD=60°，则∠AFE=＿＿＿＿，如图②，若∠BAD=90°,则∠AFE=＿＿＿＿，如图③，若若∠BAD=120°，则∠AFE=＿＿＿＿。‎ D E F C B A （2） 如图4，若∠BAD=2°，猜想∠AFE的度数，并证明。‎ A B C D E F A B C E D F G 5、 如图，已知锐角三角形ABC，分别以AB,AC为边在△ABC的形外作正方形ACFG和正方形ABDE，连接EG，若S△ABC=5，请求S△AEG。‎ B A C D O 6、 如图，A、D、B三点在同一直线上，△ADC, △BDO为等腰直角三角形。（1），AO与BC有何关系？证明你的结论。（2）当△ODB绕顶点D旋转任一角度到图②的位置，（1）中结论成立吗？请证明。‎ A B C O E