西宁中考数学试题

西宁中考数学试题

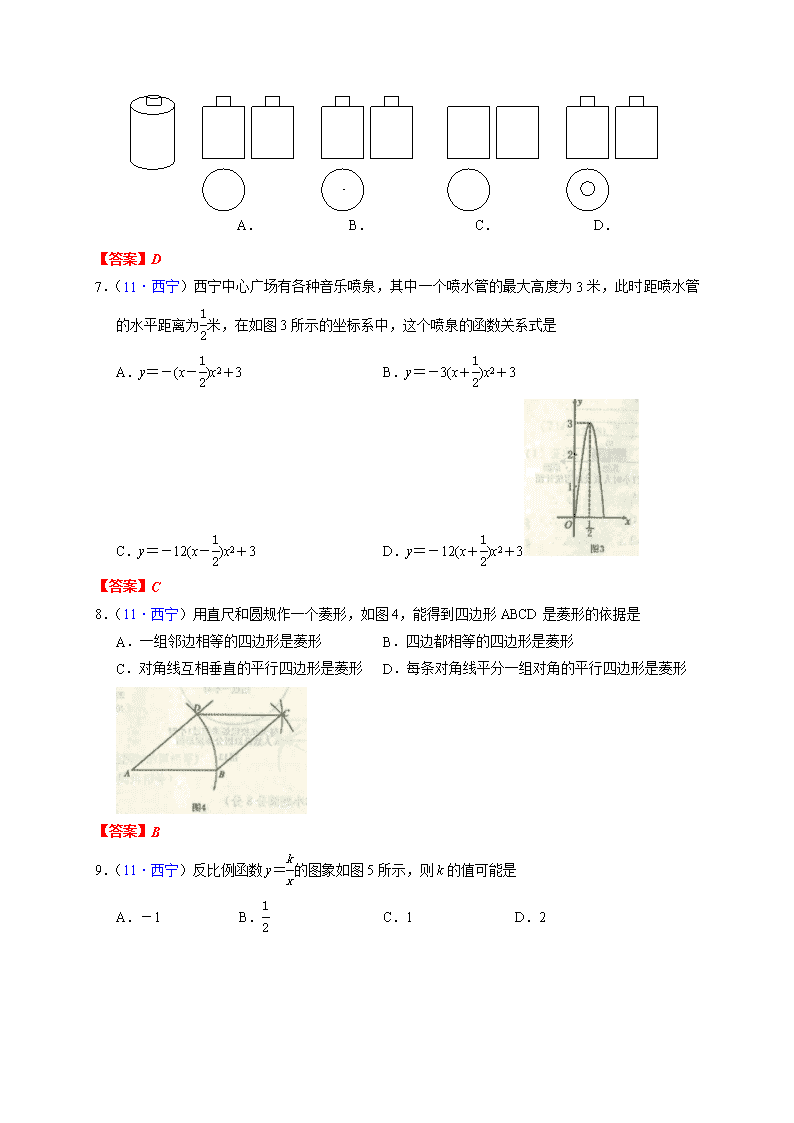
西宁市2011年高中招生考试 数学试卷 考生注意：‎ 1． 本试卷满分120分，考试时间120分钟。‎ 2． 本试卷为试题卷，不允许作为答题卷使用，答题部分请在答题卡上作答，否则无效。‎ 3． 答题前，考生务必将自己的姓名、准考证号、考点、考场、座位号写在答题卡上。同时填写在试卷上。‎ 4． 答选择题前，用2B铅笔把答题卡上对应的题目的答案标号涂黑（如需改动，用橡皮擦干净后，再选涂其他答案标号）‎ 第Ⅰ卷（选择题 共30分）‎ 一、选择题：（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项的序号填涂在答题卡上．）‎ ‎1．（11·西宁）－2＋5的相反数是 A．3 B．－3 C．－7 D．7‎ ‎【答案】B ‎2．（11·西宁）《国家中长期教育改革和发展规划纲要（2010—2020）》征求意见稿提出“财政性教育经费支出占国内生产总值比例不低于4%”，2010年我国全年国内生产总值为397983亿元．397983亿元的4%，也就是约人民币15900亿元．将15900用科学记数法表示应为 A．159×102 B．15.9×103 C．1.59×104 D．1.59×103‎ ‎【答案】C ‎3．（11·西宁）已知⊙O1、⊙O2的半径分别是r1＝2、r2＝4，若两圆相交，则圆心距O1O2可能取的值是 A．1 B．2 C．4 D．6‎ ‎【答案】C A C E F D B ‎4．（11·西宁）如图1，△DEF经过怎样的平移得到△ABC A．把△DEF向左平移4个单位，再向下平移2个单位 B．把△DEF向右平移4个单位，再向下平移2个单位 C．把△DEF向右平移4个单位，再向上平移2个单位 D．把△DEF向左平移4个单位，再向上平移2个单位 ‎【答案】A ‎5．（11·西宁）某水坝的坡度i＝1:，坡长AB＝20米，则坝的高度为 A．10米 B．20米 C．40米 D．20米 ‎【答案】A ‎6．（11·西宁）一节电池如图2所示，则它的三视图是 A．‎ B．‎ C．‎ D．‎ ‎．‎ ‎ ‎ ‎【答案】D ‎7．（11·西宁）西宁中心广场有各种音乐喷泉，其中一个喷水管的最大高度为3米，此时距喷水管的水平距离为米，在如图3所示的坐标系中，这个喷泉的函数关系式是 A．y＝－(x－)x2＋3 B．y＝－3(x＋)x2＋3 ‎ C．y＝－12(x－)x2＋3 D．y＝－12(x＋)x2＋3‎ ‎【答案】C ‎8．（11·西宁）用直尺和圆规作一个菱形，如图4，能得到四边形ABCD是菱形的依据是 A．一组邻边相等的四边形是菱形 B．四边都相等的四边形是菱形 C．对角线互相垂直的平行四边形是菱形 D．每条对角线平分一组对角的平行四边形是菱形 ‎【答案】B ‎9．（11·西宁）反比例函数y＝的图象如图5所示，则k的值可能是 A．－1 B． C．1 D．2‎ ‎【答案】B ‎10．（11·西宁）如图6，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADB＋∠EDC＝120°，BD＝3，CE＝2，则△ABC的边长为 A．9 B．12 C．16 D．18‎ ‎【答案】A 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：（本大题共10小题，每小题2分，共20分．不需要写出解答过程，请把最后结果填写在答题纸对应的位置上）．‎ ‎11．（11·西宁）计算sin45°＝_ ▲ ．‎ ‎【答案】1‎ ‎12．（11·西宁）若二次根式有意义，则x的取值范围是_ ▲ ．‎ ‎【答案】x≤ x ‎－2‎ ‎0‎ ‎2‎ y ‎－5‎ ‎－3‎ ‎－1‎ x ‎－2‎ ‎0‎ ‎2‎ ‎4‎ y ‎3‎ ‎1‎ ‎－1‎ ‎－3‎ ‎13．（11·西宁）如表1给出了直线l1上部分点(x，y)的坐标值，表2给出了直线l2上部分点(x，y)的坐标值．那么直线l1和l2直线交点坐标为_ ▲ ．‎ ‎【答案】(2，－1)‎ ‎14．（11·西宁）关于x的方程 ＋＝0的解为_ ▲ ．‎ ‎【答案】x＝－2‎ ‎15．（11·西宁）反比例函数y＝ 的图象的对称轴有_ ▲ 条．‎ ‎【答案】2‎ ‎16．（11·西宁）如图7，将直角三角形的直角顶点放在直尺的一边上，∠1＝30°，∠3＝20°，则∠2＝_ ▲ ．‎ ‎【答案】50°‎ 第21题 ‎5‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎6‎ ‎7‎ ‎8‎ O x y ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ A B C ‎17．（11·西宁）如图8，在6×6的方格纸中（共有36个小方格），每个小方格都是边长为1的正方形，将线段OA绕点O逆时针旋转得到线段OB（顶点均在格点上），则阴影部分面积等于_ ▲ ．‎ ‎【答案】2 π ‎18．（11·西宁）如图9是三种化合物的结构式及分子式，则按其规律第4个化合物的分子式为_ ▲ ．‎ ‎【答案】C4H10‎ ‎19．（11·西宁）如图10，在⊙O中，AB、AC是互相垂直的两条弦，OD⊥AB于点D，OE⊥AC于点E，且AB＝8cm，AC＝6cm，那么⊙O的半径OA长为_ ▲ ．‎ O B A C E D ‎【答案】5cm x y B A O ‎ x ‎20．（11·西宁）如图11，直线y＝kx＋b经过A(－1，1)和B(－，0)两点，则不等式0＜kx＋b＜－x的解集为_ ▲ ．‎ ‎【答案】－＜x＜－1‎ 三、解答题（本大题共8小题，第21、22题每小题7分、第23、24、25题每小题8分，第26、27每小题10分，第28题12分，共70分．解答时将文字说明、证明过程或演算步骤写在答题纸相应的位置上．）‎ ‎21．（11·西宁）（本小题满分7分）计算：()－3＋(－2011)0－｜(－2)3｜．‎ ‎【答案】原式＝27＋1－8 ………………6分 ‎＝20 ………………7分 ‎22．（11·西宁）（本小题满分7分）给出三个整式a2，b2和2ab．‎ ‎（1）当a＝3，b＝4时，求a2＋b2＋2ab的值；‎ ‎（2）在上面的三个整式中任意选择两个整式进行加法或减法运算，使所得的多项式能够因式分解．请写也你所选的式子及因式分解的过程．‎ ‎【答案】（1）当a＝3，b＝4时，a2＋b2＋2ab＝(a＋b) 2＝(3＋4) 2＝49 ………………3分 ‎（2）（答案不唯一）例：a2－b2＝(a＋b) (a－b) ………………7分 A B C D E O ‎23．（11·西宁）（本小题满分8分）如图12 ，矩形ABCD的对角线相交于点O，DE∥CA，AE∥BD．‎ ‎（1）求证：四边形AODE是菱形；‎ ‎（2）．若将题设中“矩形ABCD”这一条件改为“菱形ABCD”，‎ 其余条件不变，则四边形AODE是_ ▲ ．‎ ‎【答案】（1）证明：∵矩形ABCD的对角线相交于点O ‎∴AC＝BD（矩形对角线相等）‎ OA＝OC＝AC，OB＝OD＝BD（矩形对角线互相平分）‎ ‎∴OA＝OD ………………2分 ‎∵DE∥CA AE∥BD ‎∴四边形AODE是平行四边形（两组对边分别平行的四边形是平行四边形）‎ ‎ ………………4分 ‎∴四边形AODE是菱形（一组邻边相等的平行四边形是菱形）…………6分 ‎（2）矩形 ………………8分 ‎24．（11·西宁）（本小题满分8分）国家教育部规定“中小学生每天在校体育活动时间不少于1小时”．西宁市某中学为了了解学生体育活动的情况，随机抽查了520名毕业班学生，调查内容是：“每天锻炼是否超过1小时及未超过1小时的原因”．以下是根据所得的数据制成的统计图的一部分．‎ 根据以上信息，解答下列问题：‎ ‎（1）随机抽查的学生中每天在校锻炼时间超过1小时的人数是_ ▲ ；‎ ‎（2）请将图14补充完整；‎ ‎（3）2011年我市初中应届毕业生约为11000人，请你估计今年全市初中应届毕业生中每天锻炼时间超过1小时的学生约有多少人？‎ ‎【答案】解：（1）390 ………………2分 ‎（2）如图：‎ ‎ ………………5分 ‎（3）11000×＝8250（人） ………………8分 ‎25．（11·西宁）（本小题满分8分）如图15，阅读对话，解答问题．‎ ‎ ‎ 盒子中有三个除数字外完全相同的小球—1，1，2．‎ 小兵：我蒙上眼睛，先从盒子中摸出一个小球（摸出后不放回），用P表示我摸出小球上标有的数字．‎ 小红：你摸出后，我也蒙上眼睛，再从盒子中摸出一个小球，用Q表示我摸出小球上标有的数字．‎ ‎（1）试用树形图或列表法写出满足关于x的方程x2＋px＋q＝0的所有等可能结果；‎ ‎（2）求（1）中方程有实数根的概率．‎ ‎【答案】（1）列表 ‎2‎ ‎1‎ ‎－1‎ ‎2‎ ‎（2，1）‎ ‎（2，－1）‎ ‎1‎ ‎（1，2）‎ ‎（1，－1）‎ ‎－1‎ ‎（－1，2）‎ ‎（－1，1）‎ ‎ ………………4分 所有等可能结果：x2＋2x＋1＝0， x2＋2x－1＝0‎ x2＋x＋2＝0， x2＋x－1＝0‎ x2－x＋2＝0， x2－x＋1＝0 ………………6分 ‎（2）P（有实数根）＝ ………………8分 ‎26．（11·西宁）（本小题满分10分）已知：如图，BD为⊙O的直径，AB＝AC，AD交BC与E，AE＝2，ED＝4．‎ ‎（1）求证：△ABE∽△ADB；‎ ‎（2）求AB的长；‎ ‎（3）延长DB到F，使BF＝OB，连接FA，试判断直线FA与⊙O的位置关系，并说明理由．‎ ‎【答案】（1）∵在⊙O中，AB＝AC，‎ ‎∴＝（在同圆或等圆中，相等的弦所对的弧相等）‎ ‎∴∠ABC＝∠D（相等的弧所对的圆周角相等）‎ ‎∵∠BAD＝∠BAE ‎∴△ABE∽△ADB（如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似） ………………3分 ‎（2）解：∵△ABE∽△ADB ‎∴＝ ‎∵AE＝2，ED＝4‎ ‎∴AB＝2 ………………6分 ‎（3）直线FA与⊙O相切 ………………7分 证明：连接AO，∵BD为⊙O的直径，‎ ‎∴∠BAD＝90°（直径所对的圆周角是直角）‎ ‎∴在Rt△ABD中，AB2＋AD2＝BD2‎ ‎∴BD＝4 ∴OB＝2 ‎∵BF＝OB AB＝2 ‎∴AB＝OB＝BF ‎∴∠FAO＝90°（如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形）‎ ‎∵OA为半径 AF为⊙O切线（经过半径的外端并且垂直于这条半径的直线是圆的切线） ………………10分 ‎27．（11·西宁）（本小题满分10分）国家发改委公布的《商品房销售明码标价规定》，从‎2011年5月1日起商品房销售实行一套一标价．商品房销售价格明码标价后，可以自行降价、打折销售，但涨价必须重新申报．某市某楼盘准备以每平方米5000元的均价对外销售，由于新政策的出台，购房都持币观望．为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米4050元的均价开盘销售．‎ ‎（1）求平均每次下调的百分率；‎ ‎（2）某人准备以开盘均价购买一套100平方米的房子，开发商还给予以下两种优惠方案发供选择：‎ ‎① 打9.8折销售；② 不打折，送两年物业管理费，物业管理费是每平方米每月1.5元，请问哪种方案更优惠？‎ ‎【答案】解：（1）设平均每次下调的百分率为x，根据题意得：‎ ‎500(1－x)2＝4050 ………………4分 解此方程得：x1＝，x2＝（不符合题意，舍去）‎ ‎∴x＝10%‎ 答：平均每次下调的百分率为10% ………………7分 ‎（2）方案一：100×4050×98%＝396900（元）‎ ‎ 方案二：100×4050－1.5×100×12×2＝401400（元） ………………9分 ‎∴方案一优惠 ………………10分 ‎28．（11·西宁）（本小题满分12分）在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C为 (－1，0) ．如图17所示，B点在抛物线y＝x2＋x－2图象上，过点B作BD⊥x轴，垂足为D，且B点横坐标为－3．‎ ‎（1）求证：△BDC≌△COA；‎ ‎（2）求BC所在直线的函数关系式；‎ ‎（3）抛物线的对称轴上是否存在点P，使△ACP是以AC为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．‎ ‎【答案】（1）证明：∵∠BCD＋∠ACO＝90°，‎ ‎∠ACO＋∠OAC＝90°，‎ ‎∴∠BCD＝∠OAC ‎∵△ABC为等腰直角三角形 ∴BC＝AC 在△BDC和△COA中 ‎∠BDC＝∠COA＝90°‎ ‎∠BCD＝∠OAC BC＝AC ‎∴△BDC≌△COA（AAS） ………………4分 ‎（2）解：∵C点坐标为 (－1，0)‎ ‎∴BD＝CO＝1‎ ‎∵B点横坐标为－3‎ ‎∴B点坐标为 (－3，1)‎ 设BC所在直线的函数关系式为y＝kx＋b ‎∴ 解得 ‎∴BC所在直线的函数关系式为y＝－ x－ ………………8分 ‎（3）解：存在 ………………9分 ‎∵二次函数解析式为：y＝x2＋x－2‎ ‎∴y＝x2＋x－2‎ ‎＝(x＋)2x－ ‎∴对称轴为直线x＝－ ………………10分 若以AC为直角边，点C为直角顶点，对称轴上有一点P1，使CP1⊥AC，‎ ‎∵BC⊥AC ∵点P1为直线BC与对轴称直线x＝－的交点 由题意可得：‎ 解得： ‎∴P1（－，－）‎ 若以AC为直角边，点A为直角顶点，对称轴上有一点P2，使AP2⊥AC，‎ 则过点A作A P2∥BC，交对轴称直线x＝－于点P2‎ ‎∵CD＝OA ∴A（0，2）‎ 由题意得直线AP2的解析式为：y＝－x＋2‎ ‎ 解得： ‎∴P2（－，－）‎ ‎∴P点坐标分别为P1（－，－）、P2（－，－） ………………12分 ‎（注：每题只给出一种解法，如有不同解法请对照评分标准给分）‎