中考二次函数压轴题汇编

中考二次函数压轴题汇编

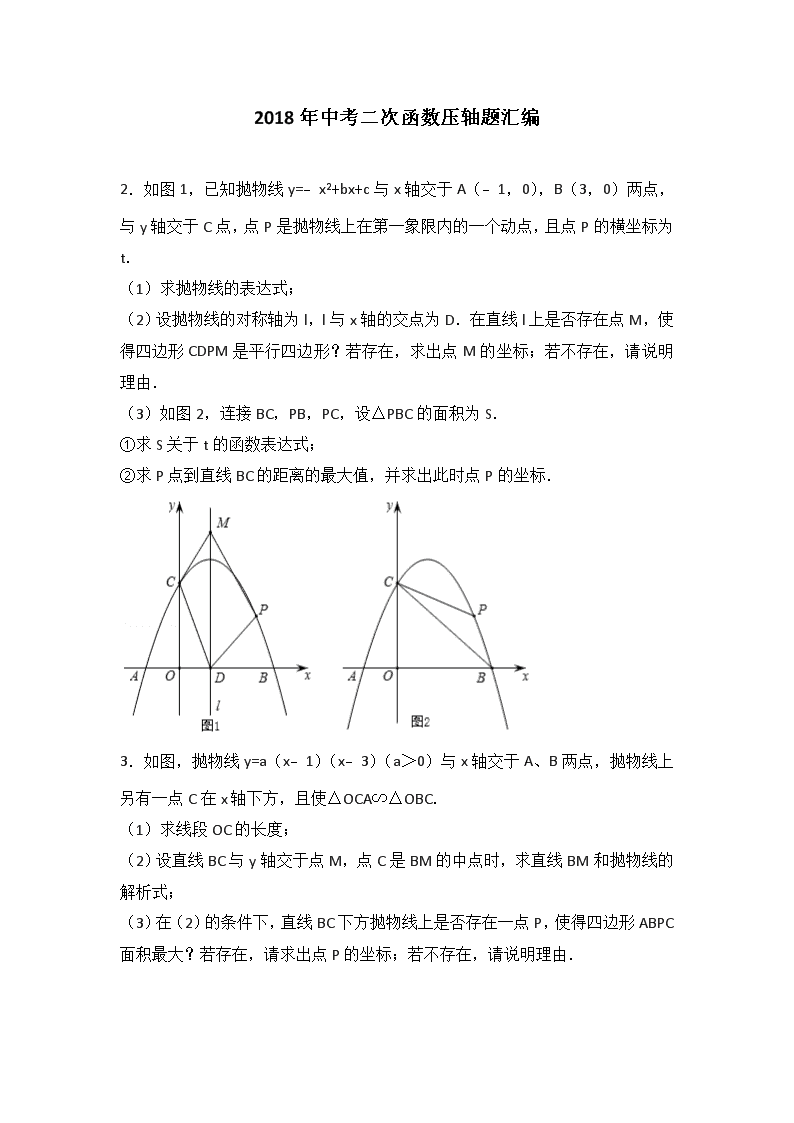
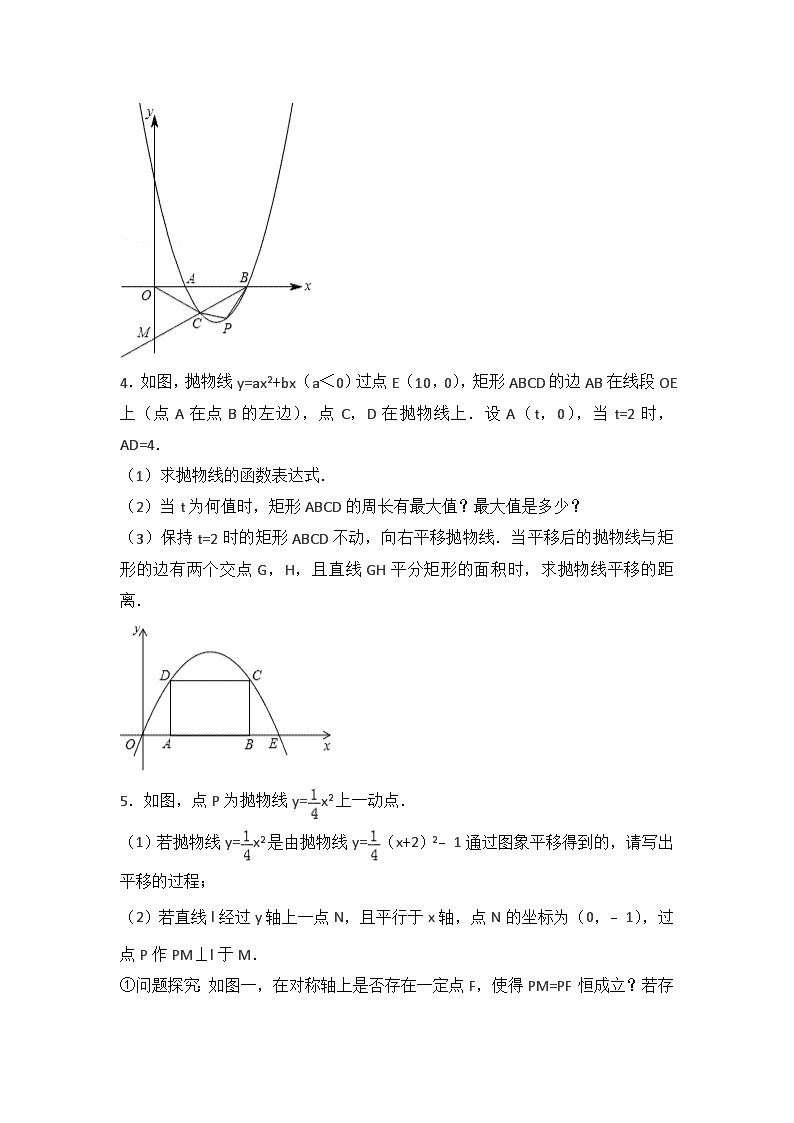
‎2018年中考二次函数压轴题汇编 ‎　‎ ‎2．如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．‎ ‎（1）求抛物线的表达式；‎ ‎（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．‎ ‎（3）如图2，连接BC，PB，PC，设△PBC的面积为S．‎ ‎①求S关于t的函数表达式；‎ ‎②求P点到直线BC的距离的最大值，并求出此时点P的坐标．‎ ‎3．如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．‎ ‎（1）求线段OC的长度；‎ ‎（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；‎ ‎（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎4．如图，抛物线y=ax2+bx（a＜0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．‎ ‎（1）求抛物线的函数表达式．‎ ‎（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？‎ ‎（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．‎ ‎5．如图，点P为抛物线y=x2上一动点．‎ ‎（1）若抛物线y=x2是由抛物线y=（x+2）2﹣1通过图象平移得到的，请写出平移的过程；‎ ‎（2）若直线l经过y轴上一点N，且平行于x轴，点N的坐标为（0，﹣1），过点P作PM⊥l于M．‎ ‎①‎ 问题探究：如图一，在对称轴上是否存在一定点F，使得PM=PF恒成立？若存在，求出点F的坐标：若不存在，请说明理由．‎ ‎②问题解决：如图二，若点Q的坐标为（1，5），求QP+PF的最小值．‎ ‎6．已知直线y=x+3与x轴、y轴分别相交于A、B两点，抛物线y=x2+bx+c经过A、B两点，点M在线段OA上，从O点出发，向点A以每秒1个单位的速度匀速运动；同时点N在线段AB上，从点A出发，向点B以每秒个单位的速度匀速运动，连接MN，设运动时间为t秒 ‎（1）求抛物线解析式；‎ ‎（2）当t为何值时，△AMN为直角三角形；‎ ‎（3）过N作NH∥y轴交抛物线于H，连接MH，是否存在点H使MH∥AB，若存在，求出点H的坐标，若不存在，请说明理由．‎ ‎7．如图，抛物线经过原点O（0，0），点A（1，1），点．‎ ‎（1）求抛物线解析式；‎ ‎（2）连接OA，过点A作AC⊥OA交抛物线于C，连接OC，求△AOC的面积；‎ ‎（3）点M是y轴右侧抛物线上一动点，连接OM，过点M作MN⊥OM交x轴于点N．问：是否存在点M，使以点O，M，N为顶点的三角形与（2）中的△AOC相似，若存在，求出点M的坐标；若不存在，说明理由．‎ ‎8．如图，已知二次函数y=ax2+1（a≠0，a为实数）的图象过点A（﹣2，2），一次函数y=kx+b（k≠0，k，b为实数）的图象l经过点B（0，2）．‎ ‎（1）求a值并写出二次函数表达式；‎ ‎（2）求b值；‎ ‎（3）设直线l与二次函数图象交于M，N两点，过M作MC垂直x轴于点C，试证明：MB=MC；‎ ‎（4）在（3）的条件下，请判断以线段MN为直径的圆与x轴的位置关系，并说明理由．‎ ‎9．如图，已知抛物线y=ax2+x+4的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．‎ ‎（1）求抛物线的解折式和A、B两点的坐标；‎ ‎（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；‎ ‎（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．‎ ‎10．已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）当点P运动到什么位置时，△PAB的面积有最大值？‎ ‎（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．‎ ‎11．如图，在平面直角坐标系中，抛物线y=x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．‎ ‎（1）求点A，B，C的坐标；‎ ‎（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；‎ ‎（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．‎ ‎12．综合与探究 如图，抛物线y=x﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC．点P是第四象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q，过点P作PE∥AC交x轴于点E，交BC于点F．‎ ‎（1）求A，B，C三点的坐标；‎ ‎（2）试探究在点P运动的过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请直接写出此时点Q的坐标；若不存在，请说明理由；‎ ‎（3）请用含m的代数式表示线段QF的长，并求出m为何值时QF有最大值．‎ ‎13．已知抛物线y=ax2+bx+c过点A（0，2）．‎ ‎（1）若点（﹣，0）也在该抛物线上，求a，b满足的关系式；‎ ‎（2）若该抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△‎ ABC有一个内角为60°．‎ ‎①求抛物线的解析式；‎ ‎②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．‎ ‎14．如图，已知抛物线y=ax2+bx与x轴分别交于原点O和点F（10，0），与对称轴l交于点E（5，5）．矩形ABCD的边AB在x轴正半轴上，且AB=1，边AD，BC与抛物线分别交于点M，N．当矩形ABCD沿x轴正方向平移，点M，N位于对称轴l的同侧时，连接MN，此时，四边形ABNM的面积记为S；点M，N位于对称轴l的两侧时，连接EM，EN，此时五边形ABNEM的面积记为S．将点A与点O重合的位置作为矩形ABCD平移的起点，设矩形ABCD平移的长度为t（0≤t≤5）．‎ ‎（1）求出这条抛物线的表达式；‎ ‎（2）当t=0时，求S△OBN的值；‎ ‎（3）当矩形ABCD沿着x轴的正方向平移时，求S关于t（0＜t≤5）的函数表达式，并求出t为何值时，S有最大值，最大值是多少？‎ ‎15．如图，已知抛物线经过点A（﹣1，0），B（4，0），C（0，2）三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P做x轴的垂线l交抛物线于点Q，交直线BD于点M．‎ ‎（1）求该抛物线所表示的二次函数的表达式；‎ ‎（2）已知点F（0，），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？‎ ‎（3）点P在线段AB运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由．‎ ‎16．如图，抛物线y=ax2﹣5ax+c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x轴上，AC=BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM=BN，连接MN，AM，AN．‎ ‎（1）求抛物线的解析式及点D的坐标；‎ ‎（2）当△CMN是直角三角形时，求点M的坐标；‎ ‎（3）试求出AM+AN的最小值．‎ ‎17．如图①，在平面直角坐标系xOy中，抛物线y=ax2+bx+3经过点A（﹣1，0）、B（3，0）两点，且与y轴交于点C．‎ ‎（1）求抛物线的表达式；‎ ‎（2）如图②，用宽为4个单位长度的直尺垂直于x轴，并沿x轴左右平移，直尺的左右两边所在的直线与抛物线相交于P、Q两点（点P在点Q的左侧），连接PQ，在线段PQ上方抛物线上有一动点D，连接DP、DQ．‎ ‎（1）若点P的横坐标为﹣，求△DPQ面积的最大值，并求此时点D的坐标；‎ ‎（Ⅱ）直尺在平移过程中，△‎ DPQ面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由．‎ ‎18．在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y=x与抛物线交于A、B两点，直线l为y=﹣1．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎（3）知F（x0，y0）为平面内一定点，M（m，n）为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．‎ ‎19．在平面直角坐标系中，点O（0，0），点A（1，0）．已知抛物线y=x2+mx﹣2m（m是常数），顶点为P．‎ ‎（Ⅰ）当抛物线经过点A时，求顶点P的坐标；‎ ‎（Ⅱ）若点P在x轴下方，当∠AOP=45°时，求抛物线的解析式；‎ ‎（Ⅲ）无论m取何值，该抛物线都经过定点H．当∠AHP=45°时，求抛物线的解析式．‎ ‎20．如图所示，将二次函数y=x2+2x+1的图象沿x轴翻折，然后向右平移1个单位，再向上平移4个单位，得到二次函数y=ax2+bx+c的图象．函数y=x2+2x+‎ ‎1的图象的顶点为点A．函数y=ax2+bx+c的图象的顶点为点B，和x轴的交点为点C，D（点D位于点C的左侧）．‎ ‎（1）求函数y=ax2+bx+c的解析式；‎ ‎（2）从点A，C，D三个点中任取两个点和点B构造三角形，求构造的三角形是等腰三角形的概率；‎ ‎（3）若点M是线段BC上的动点，点N是△ABC三边上的动点，是否存在以AM为斜边的Rt△AMN，使△AMN的面积为△ABC面积的？若存在，求tan∠MAN的值；若不存在，请说明理由．‎ ‎21．如图，已知抛物线y=ax2+bx+c（a≠0）经过点A（3，0），B（﹣1，0），C（0，﹣3）．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）若以点A为圆心的圆与直线BC相切于点M，求切点M的坐标；‎ ‎（3）若点Q在x轴上，点P在抛物线上，是否存在以点B，C，Q，P为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．‎ ‎22．已知顶点为A抛物线经过点，点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM=∠MAF，求△POE的面积；‎ ‎（3）如图2，点Q是折线A﹣B﹣C上一点，过点Q作QN∥y轴，过点E作EN∥x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标．‎ ‎23．已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若MN与直线y=﹣2x平行，且M，N位于直线BC的两侧，y1＞y2，解决以下问题：‎ ‎①求证：BC平分∠MBN；‎ ‎②求△MBC外心的纵坐标的取值范围．‎ ‎24．如图，已知二次函数的图象过点O（0，0）．A（8，4），与x轴交于另一点B，且对称轴是直线x=3．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）若M是OB上的一点，作MN∥AB交OA于N，当△ANM面积最大时，求M的坐标；‎ ‎（3）P是x轴上的点，过P作PQ⊥x轴与抛物线交于Q．过A作AC⊥x轴于C，当以O，P，Q为顶点的三角形与以O，A，C为顶点的三角形相似时，求P点的坐标．‎ ‎25．如图，抛物线y=ax2+bx+c与两坐标轴相交于点A（﹣1，0）、B（3，0）、C（0，3），D是抛物线的顶点，E是线段AB的中点．‎ ‎（1）求抛物线的解析式，并写出D点的坐标；‎ ‎（2）F（x，y）是抛物线上的动点：‎ ‎①当x＞1，y＞0时，求△BDF的面积的最大值；‎ ‎②当∠AEF=∠DBE时，求点F的坐标．‎ ‎26．如图1，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+bx+3交x轴于B、C两点（点B在左，点C在右），交y轴于点A，且OA=OC，B（﹣1，0）．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）如图2，点D为抛物线的顶点，连接CD，点P是抛物线上一动点，且在C、D两点之间运动，过点P作PE∥y轴交线段CD于点E，设点P的横坐标为t，线段PE长为d，写出d与t的关系式（不要求写出自变量t的取值范围）；‎ ‎（3）如图3，在（2）的条件下，连接BD，在BD上有一动点Q，且DQ=CE，连接EQ，当∠BQE+∠DEQ=90°时，求此时点P的坐标．‎ ‎27．已知抛物线F：y=x2+bx+c的图象经过坐标原点O，且与x轴另一交点为（﹣，0）．‎ ‎（1）求抛物线F的解析式；‎ ‎（2）如图1，直线l：y=x+m（m＞0）与抛物线F相交于点A（x1，y1）和点B（x2，y2）（点A在第二象限），求y2﹣y1的值（用含m的式子表示）；‎ ‎（3）在（2）中，若m=，设点A′是点A关于原点O的对称点，如图2．‎ ‎①判断△AA′B的形状，并说明理由；‎ ‎②平面内是否存在点P，使得以点A、B、A′、P为顶点的四边形是菱形？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎28．已知：如图，一次函数y=kx﹣1的图象经过点A（3，m）（m＞0），与y轴交于点B．点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D．若AC=CD．‎ ‎（1）求这个一次函数的表达式；‎ ‎（2）已知一开口向下、以直线CD为对称轴的抛物线经过点A，它的顶点为P，若过点P且垂直于AP的直线与x轴的交点为Q（﹣，0），求这条抛物线的函数表达式．‎ ‎29．如图，已知抛物线y=ax2+bx（a≠0）过点A（，﹣3）和点B（3，0）．过点A作直线AC∥x轴，交y轴于点C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上取一点P，过点P作直线AC的垂线，垂足为D．连接OA，使得以A，D，P为顶点的三角形与△AOC相似，求出对应点P的坐标；‎ ‎（3）抛物线上是否存在点Q，使得S△AOC=S△AOQ？若存在，求出点Q的坐标；若不存在，请说明理由．‎ ‎30．如图1，抛物线C1：y=ax2﹣2ax+c（a＜0）与x轴交于A、B两点，与y轴交于点C．已知点A的坐标为（﹣1，0），点O为坐标原点，OC=3OA，抛物线C1的顶点为G．‎ ‎（1）求出抛物线C1的解析式，并写出点G的坐标；‎ ‎（2）如图2，将抛物线C1向下平移k（k＞0）个单位，得到抛物线C2，设C2与x轴的交点为A′、B′，顶点为G′，当△A′B′G′是等边三角形时，求k的值：‎ ‎（3）在（2）的条件下，如图3，设点M为x轴正半轴上一动点，过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点，试探究在直线y=﹣1上是否存在点N，使得以P、Q、N为顶点的三角形与△AOQ全等，若存在，直接写出点M，N的坐标：若不存在，请说明理由．‎ ‎31．在平面直角坐标系中，二次函数y=ax2+x+c的图象经过点C（0，2）和点D（4，﹣2）．点E是直线y=﹣x+2与二次函数图象在第一象限内的交点．‎ ‎（1）求二次函数的解析式及点E的坐标．‎ ‎（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．‎ ‎（3）如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．‎ ‎32．如图，已知顶点为C（0，﹣3）的抛物线y=ax2+b（a≠0）与x轴交于A，B两点，直线y=x+m过顶点C和点B．‎ ‎（1）求m的值；‎ ‎（2）求函数y=ax2+b（a≠0）的解析式；‎ ‎（3）抛物线上是否存在点M，使得∠MCB=15°？若存在，求出点M的坐标；若不存在，请说明理由．‎ ‎33．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．‎ ‎（1）求抛物线的解析式和直线AC的解析式；‎ ‎（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；‎ ‎（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．‎ ‎34．已知抛物线y=a（x﹣1）2过点（3，1），D为抛物线的顶点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若点B、C均在抛物线上，其中点B（0，），且∠BDC=90°，求点C的坐标；‎ ‎（3）如图，直线y=kx+4﹣k与抛物线交于P、Q两点．‎ ‎①求证：∠PDQ=90°；‎ ‎②求△PDQ面积的最小值．‎ ‎35．抛物线y=﹣x2+x﹣1与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，其顶点为D．将抛物线位于直线l：y=t（t＜）上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．‎ ‎（1）点A，B，D的坐标分别为　 　，　 　，　 　；‎ ‎（2）如图①，抛物线翻折后，点D落在点E处．当点E在△ABC内（含边界）时，求t的取值范围；‎ ‎（3）如图②，当t=0时，若Q是“M”形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎36．如图，抛物线y=ax2+4x+c（a≠0）经过点A（﹣1，0），点E（4，5），与y轴交于点B，连接AB．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）将△ABO绕点O旋转，点B的对应点为点F．‎ ‎①当点F落在直线AE上时，求点F的坐标和△ABF的面积；‎ ‎②当点F到直线AE的距离为时，过点F作直线AE的平行线与抛物线相交，请直接写出交点的坐标．‎ ‎37．如图，在平面直角坐标系中，二次函数y=（x﹣a）（x﹣3）（0＜a＜3）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点D，过其顶点C作直线CP⊥x轴，垂足为点P，连接AD、BC．‎ ‎（1）求点A、B、D的坐标；‎ ‎（2）若△AOD与△BPC相似，求a的值；‎ ‎（3）点D、O、C、B能否在同一个圆上？若能，求出a的值；若不能，请说明理由．‎ ‎38．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于原点及点A，且经过点B（4，8），对称轴为直线x=﹣2．‎ ‎（1）求抛物线的解析式；‎ ‎（2）设直线y=kx+4与抛物线两交点的横坐标分别为x1，x2（x1＜x2），当时，求k的值；‎ ‎（3）连接OB，点P为x轴下方抛物线上一动点，过点P作OB的平行线交直线AB于点Q，当S△POQ：S△BOQ=1：2时，求出点P的坐标．‎ ‎（坐标平面内两点M（x1，y1），N（x2，y2）之间的距离MN=）‎ ‎39．如图，在平面直角坐标系中，∠ACB=90°，OC=2OB，tan∠ABC=2，点B的坐标为（1，0）．抛物线y=﹣x2+bx+c经过A、B两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE=DE．‎ ‎①求点P的坐标；‎ ‎②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．‎ ‎40．如图1，经过原点O的抛物线y=ax2+bx（a、b为常数，a≠0）与x轴相交于另一点A（3，0）．直线l：y=x在第一象限内和此抛物线相交于点B（5，t），与抛物线的对称轴相交于点C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在x轴上找一点P，使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似，求满足条件的点P的坐标；‎ ‎（3）直线l沿着x轴向右平移得到直线l′，l′与线段OA相交于点M，与x轴下方的抛物线相交于点N，过点N作NE⊥x轴于点E．把△MEN沿直线l′折叠，当点E恰好落在抛物线上时（图2），求直线l′的解析式；‎ ‎（4）在（3）问的条件下（图3），直线l′与y轴相交于点K，把△MOK绕点O顺时针旋转90°得到△M′OK′，点F为直线l′上的动点．当△M'FK′为等腰三角形时，求满足条件的点F的坐标．‎ ‎　‎ ‎2018年07月10日139****3005的初中数学组卷 参考答案与试题解析 ‎　‎ 一．选择题（共1小题）‎ ‎1．如图，点A，B在双曲线y=（x＞0）上，点C在双曲线y=（x＞0）上，若AC∥y轴，BC∥x轴，且AC=BC，则AB等于（　　）‎ A． B．2 C．4 D．3‎ ‎【解答】解：点C在双曲线y=上，AC∥y轴，BC∥x轴，‎ 设C（a，），则B（3a，），A（a，），‎ ‎∵AC=BC，‎ ‎∴﹣=3a﹣a，‎ 解得a=1，（负值已舍去）‎ ‎∴C（1，1），B（3，1），A（1，3），‎ ‎∴AC=BC=2，‎ ‎∴Rt△ABC中，AB=2，‎ 故选：B．‎ ‎　‎ 二．解答题（共39小题）‎ ‎2．如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．‎ ‎（1）求抛物线的表达式；‎ ‎（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．‎ ‎（3）如图2，连接BC，PB，PC，设△PBC的面积为S．‎ ‎①求S关于t的函数表达式；‎ ‎②求P点到直线BC的距离的最大值，并求出此时点P的坐标．‎ ‎【解答】解：（1）将A（﹣1，0）、B（3，0）代入y=﹣x2+bx+c，‎ ‎，解得：，‎ ‎∴抛物线的表达式为y=﹣x2+2x+3．‎ ‎（2）在图1中，连接PC，交抛物线对称轴l于点E，‎ ‎∵抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，‎ ‎∴抛物线的对称轴为直线x=1．‎ 当t=2时，点C、P关于直线l对称，此时存在点M，使得四边形CDPM是平行四边形．‎ ‎∵抛物线的表达式为y=﹣x2+2x+3，‎ ‎∴点C的坐标为（0，3），点P的坐标为（2，3），‎ ‎∴点M的坐标为（1，6）；‎ 当t≠2时，不存在，理由如下：‎ 若四边形CDPM是平行四边形，则CE=PE，‎ ‎∵点C的横坐标为0，点E的横坐标为0，‎ ‎∴点P的横坐标t=1×2﹣0=2．‎ 又∵t≠2，‎ ‎∴不存在．‎ ‎（3）①在图2中，过点P作PF∥y轴，交BC于点F．‎ 设直线BC的解析式为y=mx+n（m≠0），‎ 将B（3，0）、C（0，3）代入y=mx+n，‎ ‎，解得：，‎ ‎∴直线BC的解析式为y=﹣x+3．‎ ‎∵点P的坐标为（t，﹣t2+2t+3），‎ ‎∴点F的坐标为（t，﹣t+3），‎ ‎∴PF=﹣t2+2t+3﹣（﹣t+3）=﹣t2+3t，‎ ‎∴S=PF•OB=﹣t2+t=﹣（t﹣）2+．‎ ‎②∵﹣＜0，‎ ‎∴当t=时，S取最大值，最大值为．‎ ‎∵点B的坐标为（3，0），点C的坐标为（0，3），‎ ‎∴线段BC==3，‎ ‎∴P点到直线BC的距离的最大值为=，此时点P的坐标为（，）．‎ ‎　‎ ‎3．如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．‎ ‎（1）求线段OC的长度；‎ ‎（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；‎ ‎（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）由题可知当y=0时，a（x﹣1）（x﹣3）=0，‎ 解得：x1=1，x2=3，即A（1，0），B（3，0），‎ ‎∴OA=1，OB=3‎ ‎∵△OCA∽△OBC，‎ ‎∴OC：OB=OA：OC，‎ ‎∴OC2=OA•OB=3，‎ 则OC=；‎ ‎（2）∵C是BM的中点，即OC为斜边BM的中线，‎ ‎∴OC=BC，‎ ‎∴点C的横坐标为，‎ 又OC=，点C在x轴下方，‎ ‎∴C（，﹣），‎ 设直线BM的解析式为y=kx+b，‎ 把点B（3，0），C（，﹣）代入得：，‎ 解得：b=﹣，k=，‎ ‎∴y=x﹣，‎ 又∵点C（，﹣）在抛物线上，代入抛物线解析式，‎ 解得：a=，‎ ‎∴抛物线解析式为y=x2﹣x+2；‎ ‎（3）点P存在，‎ 设点P坐标为（x，x2﹣x+2），过点P作PQ⊥x轴交直线BM于点Q，‎ 则Q（x，x﹣），‎ ‎∴PQ=x﹣﹣（x2﹣x+2）=﹣x2+3x﹣3，‎ 当△BCP面积最大时，四边形ABPC的面积最大，‎ S△BCP=PQ（3﹣x）+PQ（x﹣）=PQ=﹣x2+x﹣，‎ 当x=﹣=时，S△BCP有最大值，四边形ABPC的面积最大，此时点P的坐标为（，﹣）．‎ ‎　‎ ‎4．如图，抛物线y=ax2+bx（a＜0）过点E（10，0），矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上．设A（t，0），当t=2时，AD=4．‎ ‎（1）求抛物线的函数表达式．‎ ‎（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？‎ ‎（3）保持t=2时的矩形ABCD不动，向右平移抛物线．当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离．‎ ‎【解答】解：（1）设抛物线解析式为y=ax（x﹣10），‎ ‎∵当t=2时，AD=4，‎ ‎∴点D的坐标为（2，4），‎ ‎∴将点D坐标代入解析式得﹣16a=4，‎ 解得：a=﹣，‎ 抛物线的函数表达式为y=﹣x2+x；‎ ‎（2）由抛物线的对称性得BE=OA=t，‎ ‎∴AB=10﹣2t，‎ 当x=t时，AD=﹣t2+t，‎ ‎∴矩形ABCD的周长=2（AB+AD）‎ ‎=2[（10﹣2t）+（﹣t2+t）]‎ ‎=﹣t2+t+20‎ ‎=﹣（t﹣1）2+，‎ ‎∵﹣＜0，‎ ‎∴当t=1时，矩形ABCD的周长有最大值，最大值为；‎ ‎（3）如图，‎ 当t=2时，点A、B、C、D的坐标分别为（2，0）、（8，0）、（8，4）、（2，4），‎ ‎∴矩形ABCD对角线的交点P的坐标为（5，2），‎ 当平移后的抛物线过点A时，点H的坐标为（4，4），此时GH不能将矩形面积平分；‎ 当平移后的抛物线过点C时，点G的坐标为（6，0），此时GH也不能将矩形面积平分；‎ ‎∴当G、H中有一点落在线段AD或BC上时，直线GH不可能将矩形的面积平分，‎ 当点G、H分别落在线段AB、DC上时，直线GH过点P，必平分矩形ABCD的面积，‎ ‎∵AB∥CD，‎ ‎∴线段OD平移后得到的线段GH，‎ ‎∴线段OD的中点Q平移后的对应点是P，‎ 在△OBD中，PQ是中位线，‎ ‎∴PQ=OB=4，‎ 所以抛物线向右平移的距离是4个单位．‎ ‎　‎ ‎5．如图，点P为抛物线y=x2上一动点．‎ ‎（1）若抛物线y=x2是由抛物线y=（x+2）2﹣1通过图象平移得到的，请写出平移的过程；‎ ‎（2）若直线l经过y轴上一点N，且平行于x轴，点N的坐标为（0，﹣1），过点P作PM⊥l于M．‎ ‎①问题探究：如图一，在对称轴上是否存在一定点F，使得PM=PF恒成立？若存在，求出点F的坐标：若不存在，请说明理由．‎ ‎②问题解决：如图二，若点Q的坐标为（1，5），求QP+PF的最小值．‎ ‎【解答】解：（1）∵抛物线y=（x+2）2﹣1的顶点为（﹣2，﹣1）‎ ‎∴抛物线y=（x+2）2﹣1的图象向上平移1个单位，再向右2个单位得到抛物线y=x2的图象．‎ ‎（2）①存在一定点F，使得PM=PF恒成立．‎ 如图一，过点P作PB⊥y轴于点B 设点P坐标为（a，a2）‎ ‎∴PM=PF=a2+1‎ ‎∵PB=a ‎∴Rt△PBF中 BF=‎ ‎∴OF=1‎ ‎∴点F坐标为（0，1）‎ ‎②由①，PM=PF QP+PF的最小值为QP+PM的最小值 当Q、P、M三点共线时，QP+PM有最小值，最小值为点Q纵坐标加M纵坐标的绝对值．‎ ‎∴QP+PF的最小值为6．‎ ‎　‎ ‎6．已知直线y=x+3与x轴、y轴分别相交于A、B两点，抛物线y=x2+bx+c经过A、B两点，点M在线段OA上，从O点出发，向点A以每秒1个单位的速度匀速运动；同时点N在线段AB上，从点A出发，向点B以每秒个单位的速度匀速运动，连接MN，设运动时间为t秒 ‎（1）求抛物线解析式；‎ ‎（2）当t为何值时，△AMN为直角三角形；‎ ‎（3）过N作NH∥y轴交抛物线于H，连接MH，是否存在点H使MH∥AB，若存在，求出点H的坐标，若不存在，请说明理由．‎ ‎【解答】解：（1）∵直线y=x+3与x轴、y轴分别相交于A、B两点，‎ ‎∴点A的坐标为（﹣3，0），点B的坐标为（0，3）．‎ 将A（﹣3，0）、B（0，3）代入y=x2+bx+c，得：‎ ‎，解得：，‎ ‎∴抛物线解析式为y=x2+4x+3．‎ ‎（2）当运动时间为t秒时，点M的坐标为（﹣t，0），点N的坐标为（t﹣3，t），‎ ‎∴AM=3﹣t，AN=t．‎ ‎∵△AMN为直角三角形，∠MAN=45°，‎ ‎∴△AMN为等腰直角三角形（如图1）．‎ 当∠ANM=90°时，有AM=AN，即3﹣t=2t，‎ 解得：t=1；‎ 当∠AMN=90°时，有t﹣3=﹣t，‎ 解得：t=．‎ 综上所述：当t为1秒或秒时，△AMN为直角三角形．‎ ‎（3）设NH与x轴交于点E，如图2所示．‎ 当运动时间为t秒时，点M的坐标为（﹣t，0），点N的坐标为（t﹣3，t），‎ ‎∴点E的坐标为（t﹣3，0），点H的坐标为（t﹣3，t2﹣2t）．‎ ‎∵MH∥AB，‎ ‎∴∠EMH=45°，‎ ‎∴△EMH为等腰直角三角形，‎ ‎∴ME=HE，即|2t﹣3|=|t2﹣2t|，‎ 解得：t1=1，t2=3（舍去），t3=，t4=﹣（舍去）．‎ 当t=时，点E在点M的右边，点H在x轴下方，‎ ‎∴此时MH⊥AB，‎ ‎∴t=1．‎ ‎∴存在点H使MH∥AB，点H的坐标为（﹣2，﹣1）．‎ ‎　‎ ‎7．如图，抛物线经过原点O（0，0），点A（1，1），点．‎ ‎（1）求抛物线解析式；‎ ‎（2）连接OA，过点A作AC⊥OA交抛物线于C，连接OC，求△AOC的面积；‎ ‎（3）点M是y轴右侧抛物线上一动点，连接OM，过点M作MN⊥OM交x轴于点N．问：是否存在点M，使以点O，M，N为顶点的三角形与（2）中的△AOC相似，若存在，求出点M的坐标；若不存在，说明理由．‎ ‎【解答】解：（1）设抛物线解析式为y=ax（x﹣），‎ 把A（1，1）代入得a•1（1﹣）=1，解得a=﹣，‎ ‎∴抛物线解析式为y=﹣x（x﹣），‎ 即y=﹣x2+x；‎ ‎（2）延长CA交y轴于D，如图1，‎ ‎∵A（1，1），‎ ‎∴OA=，∠DOA=45°，‎ ‎∴△AOD为等腰直角三角形，‎ ‎∵OA⊥AC，‎ ‎∴OD=OA=2，‎ ‎∴D（0，2），‎ 易得直线AD的解析式为y=﹣x+2，‎ 解方程组得或，则C（5，﹣3），‎ ‎∴S△AOC=S△COD﹣S△AOD ‎=×2×5﹣×2×1‎ ‎=4；‎ ‎（3）存在．‎ 如图2，作MH⊥x轴于H，AC==4，OA=，‎ 设M（x，﹣x2+x）（x＞0），‎ ‎∵∠OHM=∠OAC，‎ ‎∴当=时，△OHM∽△OAC，即=，‎ 解方程﹣x2+x=4x得x1=0（舍去），x2=﹣（舍去），‎ 解方程﹣x2+x=﹣4x得x1=0（舍去），x2=，此时M点坐标为（，﹣54）；‎ 当=时，△OHM∽△CAO，即=，‎ 解方程﹣x2+x=x得x1=0（舍去），x2=，此时M点的坐标为（，），‎ 解方程﹣x2+x=﹣x得x1=0（舍去），x2=﹣，此时M点坐标为（，﹣）；‎ ‎∵MN⊥OM，‎ ‎∴∠OMN=90°，‎ ‎∴∠MON=∠HOM，‎ ‎∴△OMH∽△ONM，‎ ‎∴当M点的坐标为（，﹣54）或（，）或（，﹣‎ ‎）时，以点O，M，N为顶点的三角形与（2）中的△AOC相似．‎ ‎　‎ ‎8．如图，已知二次函数y=ax2+1（a≠0，a为实数）的图象过点A（﹣2，2），一次函数y=kx+b（k≠0，k，b为实数）的图象l经过点B（0，2）．‎ ‎（1）求a值并写出二次函数表达式；‎ ‎（2）求b值；‎ ‎（3）设直线l与二次函数图象交于M，N两点，过M作MC垂直x轴于点C，试证明：MB=MC；‎ ‎（4）在（3）的条件下，请判断以线段MN为直径的圆与x轴的位置关系，并说明理由．‎ ‎【解答】解：（1）∵二次函数y=ax2+1（a≠0，a为实数）的图象过点A（﹣2，2），‎ ‎∴2=4a+1，解得：a=，‎ ‎∴二次函数表达式为y=x2+1．‎ ‎（2）∵一次函数y=kx+b（k≠0，k，b为实数）的图象l经过点B（0，2），‎ ‎∴2=k×0+b，‎ ‎∴b=2．‎ ‎（3）证明：过点M作ME⊥y轴于点E，如图1所示．‎ 设点M的坐标为（x，x2+1），则MC=x2+1，‎ ‎∴ME=|x|，EB=|x2+1﹣2|=|x2﹣1|，‎ ‎∴MB=，‎ ‎=，‎ ‎=，‎ ‎=，‎ ‎=x2+1．‎ ‎∴MB=MC．‎ ‎（4）相切，理由如下：‎ 过点N作ND⊥x轴于D，取MN的中点为P，过点P作PF⊥x轴于点F，过点N作NH⊥MC于点H，交PF于点Q，如图2所示．‎ 由（3）知NB=ND，‎ ‎∴MN=NB+MB=ND+MC．‎ ‎∵点P为MN的中点，PQ∥MH，‎ ‎∴PQ=MH．‎ ‎∵ND∥HC，NH∥DC，且四个角均为直角，‎ ‎∴四边形NDCH为矩形，‎ ‎∴QF=ND，‎ ‎∴PF=PQ+QF=MH+ND=（ND+MH+HC）=（ND+MC）=MN．‎ ‎∴以MN为直径的圆与x轴相切．‎ ‎　‎ ‎9．如图，已知抛物线y=ax2+x+4的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．‎ ‎（1）求抛物线的解折式和A、B两点的坐标；‎ ‎（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；‎ ‎（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．‎ ‎【解答】解：（1）∵抛物线y=ax2+x+4的对称轴是直线x=3，‎ ‎∴﹣=3，解得：a=﹣，‎ ‎∴抛物线的解析式为y=﹣x2+x+4．‎ 当y=0时，﹣x2+x+4=0，‎ 解得：x1=﹣2，x2=8，‎ ‎∴点A的坐标为（﹣2，0），点B的坐标为（8，0）．‎ ‎（2）当x=0时，y=﹣x2+x+4=4，‎ ‎∴点C的坐标为（0，4）．‎ 设直线BC的解析式为y=kx+b（k≠0）．‎ 将B（8，0）、C（0，4）代入y=kx+b，‎ ‎，解得：，‎ ‎∴直线BC的解析式为y=﹣x+4．‎ 假设存在，设点P的坐标为（x，﹣x2+x+4），过点P作PD∥y轴，交直线BC于点D，则点D的坐标为（x，﹣x+4），如图所示．‎ ‎∴PD=﹣x2+x+4﹣（﹣x+4）=﹣x2+2x，‎ ‎∴S△PBC=PD•OB=×8•（﹣x2+2x）=﹣x2+8x=﹣（x﹣4）2+16．‎ ‎∵﹣1＜0，‎ ‎∴当x=4时，△PBC的面积最大，最大面积是16．‎ ‎∵0＜x＜8，‎ ‎∴存在点P，使△PBC的面积最大，最大面积是16．‎ ‎（3）设点M的坐标为（m，﹣m2+m+4），则点N的坐标为（m，﹣m+4），‎ ‎∴MN=|﹣m2+m+4﹣（﹣m+4）|=|﹣m2+2m|．‎ 又∵MN=3，‎ ‎∴|﹣m2+2m|=3．‎ 当0＜m＜8时，有﹣m2+2m﹣3=0，‎ 解得：m1=2，m2=6，‎ ‎∴点P的坐标为（2，6）或（6，4）；‎ 当m＜0或m＞8时，有﹣m2+2m+3=0，‎ 解得：m3=4﹣2，m4=4+2，‎ ‎∴点P的坐标为（4﹣2，﹣1）或（4+2，﹣﹣1）．‎ 综上所述：M点的坐标为（4﹣2，﹣1）、（2，6）、（6，4）或（4+2，﹣﹣1）．‎ ‎　‎ ‎10．已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）当点P运动到什么位置时，△PAB的面积有最大值？‎ ‎（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．‎ ‎【解答】解：（1）∵抛物线过点B（6，0）、C（﹣2，0），‎ ‎∴设抛物线解析式为y=a（x﹣6）（x+2），‎ 将点A（0，6）代入，得：﹣12a=6，‎ 解得：a=﹣，‎ 所以抛物线解析式为y=﹣（x﹣6）（x+2）=﹣x2+2x+6；‎ ‎（2）如图1，过点P作PM⊥OB与点M，交AB于点N，作AG⊥PM于点G，‎ 设直线AB解析式为y=kx+b，‎ 将点A（0，6）、B（6，0）代入，得：‎ ‎，‎ 解得：，‎ 则直线AB解析式为y=﹣x+6，‎ 设P（t，﹣t2+2t+6）其中0＜t＜6，‎ 则N（t，﹣t+6），‎ ‎∴PN=PM﹣MN=﹣t2+2t+6﹣（﹣t+6）=﹣t2+2t+6+t﹣6=﹣t2+3t，‎ ‎∴S△PAB=S△PAN+S△PBN ‎=PN•AG+PN•BM ‎=PN•（AG+BM）‎ ‎=PN•OB ‎=×（﹣t2+3t）×6‎ ‎=﹣t2+9t ‎=﹣（t﹣3）2+，‎ ‎∴当t=3时，△PAB的面积有最大值；‎ ‎（3）如图2，‎ ‎∵PH⊥OB于H，‎ ‎∴∠DHB=∠AOB=90°，‎ ‎∴DH∥AO，‎ ‎∵OA=OB=6，‎ ‎∴∠BDH=∠BAO=45°，‎ ‎∵PE∥x轴、PD⊥x轴，‎ ‎∴∠DPE=90°，‎ 若△PDE为等腰直角三角形，‎ 则PD=PE，‎ 设点P的横坐标为a，‎ ‎∴PD=﹣a2+2a+6﹣（﹣a+6）=﹣a2+3a，PE=2|2﹣a|，‎ ‎∴﹣a2+3a=2|2﹣a|，‎ 解得：a=4或a=5﹣，‎ 所以P（4，6）或P（5﹣，3﹣5）．‎ ‎　‎ ‎11．如图，在平面直角坐标系中，抛物线y=x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．‎ ‎（1）求点A，B，C的坐标；‎ ‎（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；‎ ‎（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）当x=0时，y=x2﹣x﹣4=﹣4，‎ ‎∴点C的坐标为（0，﹣4）；‎ 当y=0时，有x2﹣x﹣4=0，‎ 解得：x1=﹣2，x2=3，‎ ‎∴点A的坐标为（﹣2，0），点B的坐标为（3，0）．‎ ‎（2）设直线BC的解析式为y=kx+b（k≠0），‎ 将B（3，0）、C（0，﹣4）代入y=kx+b，‎ ‎，解得：，‎ ‎∴直线BC的解析式为y=x﹣4．‎ 过点Q作QE∥y轴，交x轴于点E，如图1所示，‎ 当运动时间为t秒时，点P的坐标为（2t﹣2，0），点Q的坐标为（3﹣t，﹣t），‎ ‎∴PB=3﹣（2t﹣2）=5﹣2t，QE=t，‎ ‎∴S△PBQ=PB•QE=﹣t2+2t=﹣（t﹣）2+．‎ ‎∵﹣＜0，‎ ‎∴当t=时，△PBQ的面积取最大值，最大值为．‎ ‎（3）当△PBQ面积最大时，t=，‎ 此时点P的坐标为（，0），点Q的坐标为（，﹣1）．‎ 假设存在，设点M的坐标为（m，m2﹣m﹣4），则点F的坐标为（m，m﹣4），‎ ‎∴MF=m﹣4﹣（m2﹣m﹣4）=﹣m2+2m，‎ ‎∴S△BMC=MF•OB=﹣m2+3m．‎ ‎∵△BMC的面积是△PBQ面积的1.6倍，‎ ‎∴﹣m2+3m=×1.6，即m2﹣3m+2=0，‎ 解得：m1=1，m2=2．‎ ‎∵0＜m＜3，‎ ‎∴在BC下方的抛物线上存在点M，使△BMC的面积是△PBQ面积的1.6倍，点M的坐标为（1，﹣4）或（2，﹣）．‎ ‎　‎ ‎12．综合与探究 如图，抛物线y=x﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC．点P是第四象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q，过点P作PE∥AC交x轴于点E，交BC于点F．‎ ‎（1）求A，B，C三点的坐标；‎ ‎（2）试探究在点P运动的过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请直接写出此时点Q的坐标；若不存在，请说明理由；‎ ‎（3）请用含m的代数式表示线段QF的长，并求出m为何值时QF有最大值．‎ ‎【解答】解：（1）当y=0，x﹣4=0，解得x1=﹣3，x2=4，‎ ‎∴A（﹣3，0），B（4，0），‎ 当x=0，y=x﹣4=﹣4，‎ ‎∴C（0，﹣4）；‎ ‎（2）AC==5，‎ 易得直线BC的解析式为y=x﹣4，‎ 设Q（m，m﹣4）（0＜m＜4），‎ 当CQ=CA时，m2+（m﹣4+4）2=52，解得m1=，m2=﹣（舍去），此时Q点坐标为（，﹣4）；‎ 当AQ=AC时，（m+3）2+（m﹣4）2=52，解得m1=1，m2=0（舍去），此时Q点坐标为（1，﹣3）；‎ 当QA=QC时，（m+3）2+（m﹣4）2=52，解得m=（舍去），‎ 综上所述，满足条件的Q点坐标为（，﹣4）或（1，﹣3）；‎ ‎（3）解：过点F作FG⊥PQ于点G，如图，‎ 则FG∥x轴．由B（4，0），C（0，﹣4）得△OBC为等腰直角三角形 ‎∴∠OBC=∠QFG=45 ‎ ‎∴△FQG为等腰直角三角形，‎ ‎∴FG=QG=FQ，‎ ‎∵PE∥AC，PG∥CO，‎ ‎∴∠FPG=∠ACO，‎ ‎∵∠FGP=∠AOC=90°，‎ ‎∴△FGP～△AOC．‎ ‎∴=，即=，‎ ‎∴PG=FG=•FQ=FQ，‎ ‎∴PQ=PG+GQ=FQ+FQ=FQ，‎ ‎∴FQ=PQ，‎ 设P（m，m2﹣m﹣4）（0＜m＜4），则Q（m，m﹣4），‎ ‎∴PQ=m﹣4﹣（m2﹣m﹣4）=﹣m2+m，‎ ‎∴FQ=（﹣m2+m）=﹣（m﹣2）2+‎ ‎∵﹣＜0，‎ ‎∴QF有最大值．‎ ‎∴当m=2时，QF有最大值．‎ ‎　‎ ‎13．已知抛物线y=ax2+bx+c过点A（0，2）．‎ ‎（1）若点（﹣，0）也在该抛物线上，求a，b满足的关系式；‎ ‎（2）若该抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为心，OA为半径的圆与拋物线的另两个交点为B，C，且△ABC有一个内角为60°．‎ ‎①求抛物线的解析式；‎ ‎②若点P与点O关于点A对称，且O，M，N三点共线，求证：PA平分∠MPN．‎ ‎【解答】解：（1）∵抛物线y=ax2+bx+c过点A（0，2），‎ ‎∴c=2．‎ 又∵点（﹣，0）也在该抛物线上，‎ ‎∴a（﹣）2+b（﹣）+c=0，‎ ‎∴2a﹣b+2=0（a≠0）．‎ ‎（2）①∵当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0，‎ ‎∴x1﹣x2＜0，y1﹣y2＜0，‎ ‎∴当x＜0时，y随x的增大而增大；‎ 同理：当x＞0时，y随x的增大而减小，‎ ‎∴抛物线的对称轴为y轴，开口向下，‎ ‎∴b=0．‎ ‎∵OA为半径的圆与拋物线的另两个交点为B、C，‎ ‎∴△ABC为等腰三角形，‎ 又∵△ABC有一个内角为60°，‎ ‎∴△ABC为等边三角形．‎ 设线段BC与y轴交于点D，则BD=CD，且∠OCD=30°，‎ 又∵OB=OC=OA=2，‎ ‎∴CD=OC•cos30°=，OD=OC•sin30°=1．‎ 不妨设点C在y轴右侧，则点C的坐标为（，﹣1）．‎ ‎∵点C在抛物线上，且c=2，b=0，‎ ‎∴3a+2=﹣1，‎ ‎∴a=﹣1，‎ ‎∴抛物线的解析式为y=﹣x2+2．‎ ‎②证明：由①可知，点M的坐标为（x1，﹣+2），点N的坐标为（x2，﹣+2）．‎ 直线OM的解析式为y=k1x（k1≠0）．‎ ‎∵O、M、N三点共线，‎ ‎∴x1≠0，x2≠0，且=，‎ ‎∴﹣x1+=﹣x2+，‎ ‎∴x1﹣x2=﹣，‎ ‎∴x1x2=﹣2，即x2=﹣，‎ ‎∴点N的坐标为（﹣，﹣+2）．‎ 设点N关于y轴的对称点为点N′，则点N′的坐标为（，﹣+2）．‎ ‎∵点P是点O关于点A的对称点，‎ ‎∴OP=2OA=4，‎ ‎∴点P的坐标为（0，4）．‎ 设直线PM的解析式为y=k2x+4，‎ ‎∵点M的坐标为（x1，﹣+2），‎ ‎∴﹣+2=k2x1+4，‎ ‎∴k2=﹣，‎ ‎∴直线PM的解析式为y=﹣x+4．‎ ‎∵﹣•+4==﹣+2，‎ ‎∴点N′在直线PM上，‎ ‎∴PA平分∠MPN．‎ ‎　‎ ‎14．如图，已知抛物线y=ax2+bx与x轴分别交于原点O和点F（10，0），与对称轴l交于点E（5，5）．矩形ABCD的边AB在x轴正半轴上，且AB=1，边AD，BC与抛物线分别交于点M，N．当矩形ABCD沿x轴正方向平移，点M，N位于对称轴l的同侧时，连接MN，此时，四边形ABNM的面积记为S；点M，N位于对称轴l的两侧时，连接EM，EN，此时五边形ABNEM的面积记为S．将点A与点O重合的位置作为矩形ABCD平移的起点，设矩形ABCD平移的长度为t（0≤t≤5）．‎ ‎（1）求出这条抛物线的表达式；‎ ‎（2）当t=0时，求S△OBN的值；‎ ‎（3）当矩形ABCD沿着x轴的正方向平移时，求S关于t（0＜t≤5）的函数表达式，并求出t为何值时，S有最大值，最大值是多少？‎ ‎【解答】解：（1）将E（5，5）、F（10，0）代入y=ax2+bx，‎ ‎，解得：，‎ ‎∴抛物线的表达式为y=﹣x2+2x．‎ ‎（2）当t=0时，点B的坐标为（1，0），点N的坐标为（1，），‎ ‎∴BN=，OB=1，‎ ‎∴S△OBN=BN•OB=．‎ ‎（3）①当0＜t≤4时（图1），点A的坐标为（t，0），点B的坐标为（t+1，0），‎ ‎∴点M的坐标为（t，﹣t2+2t），点N的坐标为（t+1，﹣（t+1）2+2（t+1）），‎ ‎∴AM=﹣t2+2t，BN=﹣（t+1）2+2（t+1），‎ ‎∴S=（AM+BN）•AB=×1×[﹣t2+2t﹣（t+1）2+2（t+1）]，‎ ‎=﹣t2+t+，‎ ‎=﹣（t﹣）2+，‎ ‎∵﹣＜0，‎ ‎∴当t=4时，S取最大值，最大值为；‎ ‎②当4＜t≤5时（图2），点A的坐标为（t，0），点B的坐标为（t+1，0），‎ ‎∴点M的坐标为（t，﹣t2+2t），点N的坐标为（t+1，﹣（t+1）2+2（t+1）），‎ ‎∴AM=﹣t2+2t，BN=﹣（t+1）2+2（t+1），‎ ‎∴S=（5﹣t）（﹣t2+2t+5）+（t﹣4）[5﹣（t+1）2+2（t+1）]，‎ ‎=（t3﹣3t2+5t+25）+（﹣t3+t2+t﹣），‎ ‎=﹣t2+t﹣，‎ ‎=﹣（t﹣）2+，‎ ‎∵﹣＜0，‎ ‎∴当t=时，S取最大值，最大值为．‎ ‎∵=＜，‎ ‎∴当t=时，S有最大值，最大值是．‎ ‎　‎ ‎15．如图，已知抛物线经过点A（﹣1，0），B（4，0），C（0，2）三点，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P做x轴的垂线l交抛物线于点Q，交直线BD于点M．‎ ‎（1）求该抛物线所表示的二次函数的表达式；‎ ‎（2）已知点F（0，），当点P在x轴上运动时，试求m为何值时，四边形DMQF是平行四边形？‎ ‎（3）点P在线段AB运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由．‎ ‎【解答】‎ 解：（1）由抛物线过点A（﹣1，0）、B（4，0）可设解析式为y=a（x+1）（x﹣4），‎ 将点C（0，2）代入，得：﹣4a=2，‎ 解得：a=﹣，‎ 则抛物线解析式为y=﹣（x+1）（x﹣4）=﹣x2+x+2；‎ ‎（2）由题意知点D坐标为（0，﹣2），‎ 设直线BD解析式为y=kx+b，‎ 将B（4，0）、D（0，﹣2）代入，得：，‎ 解得：，‎ ‎∴直线BD解析式为y=x﹣2，‎ ‎∵QM⊥x轴，P（m，0），‎ ‎∴Q（m，﹣m2+m+2）、M（m，m﹣2），‎ 则QM=﹣m2+m+2﹣（m﹣2）=﹣m2+m+4，‎ ‎∵F（0，）、D（0，﹣2），‎ ‎∴DF=，‎ ‎∵QM∥DF，‎ ‎∴当﹣m2+m+4=时，四边形DMQF是平行四边形，‎ 解得：m=﹣1（舍）或m=3，‎ 即m=3时，四边形DMQF是平行四边形；‎ ‎（3）如图所示：‎ ‎∵QM∥DF，‎ ‎∴∠ODB=∠QMB，‎ 分以下两种情况：‎ ‎①当∠DOB=∠MBQ=90°时，△DOB∽△MBQ，‎ 则===，‎ ‎∵∠MBQ=90°，‎ ‎∴∠MBP+∠PBQ=90°，‎ ‎∵∠MPB=∠BPQ=90°，‎ ‎∴∠MBP+∠BMP=90°，‎ ‎∴∠BMP=∠PBQ，‎ ‎∴△MBQ∽△BPQ，‎ ‎∴=，即=，‎ 解得：m1=3、m2=4，‎ 当m=4时，点P、Q、M均与点B重合，不能构成三角形，舍去，‎ ‎∴m=3，点Q的坐标为（3，2）；‎ ‎②当∠BQM=90°时，此时点Q与点A重合，△BOD∽△BQM′，‎ 此时m=﹣1，点Q的坐标为（﹣1，0）；‎ 综上，点Q的坐标为（3，2）或（﹣1，0）时，以点B、Q、M为顶点的三角形与△BOD相似．‎ ‎　‎ ‎16．如图，抛物线y=ax2﹣5ax+c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x轴上，AC=BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM=BN，连接MN，AM，AN．‎ ‎（1）求抛物线的解析式及点D的坐标；‎ ‎（2）当△CMN是直角三角形时，求点M的坐标；‎ ‎（3）试求出AM+AN的最小值．‎ ‎【解答】解：（1）把A（﹣3，0），C（0，4）代入y=ax2﹣5ax+c得，解得，‎ ‎∴抛物线解析式为y=﹣x2+x+4；‎ ‎∵AC=BC，CO⊥AB，‎ ‎∴OB=OA=3，‎ ‎∴B（3，0），‎ ‎∵BD⊥x轴交抛物线于点D，‎ ‎∴D点的横坐标为3，‎ 当x=3时，y=﹣×9+×3+4=5，‎ ‎∴D点坐标为（3，5）；‎ ‎（2）在Rt△OBC中，BC===5，‎ 设M（0，m），则BN=4﹣m，CN=5﹣（4﹣m）=m+1，‎ ‎∵∠MCN=∠OCB，‎ ‎∴当=时，△CMN∽△COB，则∠CMN=∠COB=90°，即=，解得m=‎ ‎，此时M点坐标为（0，）；‎ 当=时，△CMN∽△CBO，则∠CNM=∠COB=90°，即=，解得m=，此时M点坐标为（0，）；‎ 综上所述，M点的坐标为（0，）或（0，）；‎ ‎（3）连接DN，AD，如图，‎ ‎∵AC=BC，CO⊥AB，‎ ‎∴OC平分∠ACB，‎ ‎∴∠ACO=∠BCO，‎ ‎∵BD∥OC，‎ ‎∴∠BCO=∠DBC，‎ ‎∵DB=BC=AC=5，CM=BN，‎ ‎∴△ACM≌△DBN，‎ ‎∴AM=DN，‎ ‎∴AM+AN=DN+AN，‎ 而DN+AN≥AD（当且仅当点A、N、D共线时取等号），‎ ‎∴DN+AN的最小值==，‎ ‎∴AM+AN的最小值为．‎ ‎　‎ ‎17．如图①，在平面直角坐标系xOy中，抛物线y=ax2+bx+3经过点A（﹣1，0）、B（3，0）两点，且与y轴交于点C．‎ ‎（1）求抛物线的表达式；‎ ‎（2）如图②‎ ‎，用宽为4个单位长度的直尺垂直于x轴，并沿x轴左右平移，直尺的左右两边所在的直线与抛物线相交于P、Q两点（点P在点Q的左侧），连接PQ，在线段PQ上方抛物线上有一动点D，连接DP、DQ．‎ ‎（1）若点P的横坐标为﹣，求△DPQ面积的最大值，并求此时点D的坐标；‎ ‎（Ⅱ）直尺在平移过程中，△DPQ面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由．‎ ‎【解答】解：（1）将A（﹣1，0）、B（3，0）代入y=ax2+bx+3，得：‎ ‎，解得：，‎ ‎∴抛物线的表达式为y=﹣x2+2x+3．‎ ‎（2）（I）当点P的横坐标为﹣时，点Q的横坐标为，‎ ‎∴此时点P的坐标为（﹣，），点Q的坐标为（，﹣）．‎ 设直线PQ的表达式为y=mx+n，‎ 将P（﹣，）、Q（，﹣）代入y=mx+n，得：‎ ‎，解得：，‎ ‎∴直线PQ的表达式为y=﹣x+．‎ 如图②，过点D作DE∥y轴交直线PQ于点E，‎ 设点D的坐标为（x，﹣x2+2x+3），则点E的坐标为（x，﹣x+），‎ ‎∴DE=﹣x2+2x+3﹣（﹣x+）=﹣x2+3x+，‎ ‎∴S△DPQ=DE•（xQ﹣xP）=﹣2x2+6x+=﹣2（x﹣）2+8．‎ ‎∵﹣2＜0，‎ ‎∴当x=时，△DPQ的面积取最大值，最大值为8，此时点D的坐标为（，）．‎ ‎（II）假设存在，设点P的横坐标为t，则点Q的横坐标为4+t，‎ ‎∴点P的坐标为（t，﹣t2+2t+3），点Q的坐标为（4+t，﹣（4+t）2+2（4+t）+3），‎ 利用待定系数法易知，直线PQ的表达式为y=﹣2（t+1）x+t2+4t+3．‎ 设点D的坐标为（x，﹣x2+2x+3），则点E的坐标为（x，﹣2（t+1）x+t2+4t+3），‎ ‎∴DE=﹣x2+2x+3﹣[﹣2（t+1）x+t2+4t+3]=﹣x2+2（t+2）x﹣t2﹣4t，‎ ‎∴S△DPQ=DE•（xQ﹣xP）=﹣2x2+4（t+2）x﹣2t2﹣8t=﹣2[x﹣（t+2）]2+8．‎ ‎∵﹣2＜0，‎ ‎∴当x=t+2时，△DPQ的面积取最大值，最大值为8．‎ ‎∴假设成立，即直尺在平移过程中，△DPQ面积有最大值，面积的最大值为8．‎ ‎　‎ ‎18．在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y=x与抛物线交于A、B两点，直线l为y=﹣1．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎（3）知F（x0，y0）为平面内一定点，M（m，n）为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．‎ ‎【解答】解：（1）∵抛物线的顶点坐标为（2，0），‎ 设抛物线的解析式为y=a（x﹣2）2．‎ ‎∵该抛物线经过点（4，1），‎ ‎∴1=4a，解得：a=，‎ ‎∴抛物线的解析式为y=（x﹣2）2=x2﹣x+1．‎ ‎（2）联立直线AB与抛物线解析式成方程组，得：‎ ‎，解得：，，‎ ‎∴点A的坐标为（1，），点B的坐标为（4，1）．‎ 作点B关于直线l的对称点B′，连接AB′交直线l于点P，此时PA+PB取得最小值（如图1所示）．‎ ‎∵点B（4，1），直线l为y=﹣1，‎ ‎∴点B′的坐标为（4，﹣3）．‎ 设直线AB′的解析式为y=kx+b（k≠0），‎ 将A（1，）、B′（4，﹣3）代入y=kx+b，得：‎ ‎，解得：，‎ ‎∴直线AB′的解析式为y=﹣x+，‎ 当y=﹣1时，有﹣x+=﹣1，‎ 解得：x=，‎ ‎∴点P的坐标为（，﹣1）．‎ ‎（3）∵点M到直线l的距离与点M到点F的距离总是相等，‎ ‎∴（m﹣x0）2+（n﹣y0）2=（n+1）2，‎ ‎∴m2﹣2x0m+x02﹣2y0n+y02=2n+1．‎ ‎∵M（m，n）为抛物线上一动点，‎ ‎∴n=m2﹣m+1，‎ ‎∴m2﹣2x0m+x02﹣2y0（m2﹣m+1）+y02=2（m2﹣m+1）+1，‎ 整理得：（1﹣﹣y0）m2+（2﹣2x0+2y0）m+x02+y02﹣2y0﹣3=0．‎ ‎∵m为任意值，‎ ‎∴，‎ ‎∴，‎ ‎∴定点F的坐标为（2，1）．‎ ‎　‎ ‎19．在平面直角坐标系中，点O（0，0），点A（1，0）．已知抛物线y=x2+mx﹣2m（m是常数），顶点为P．‎ ‎（Ⅰ）当抛物线经过点A时，求顶点P的坐标；‎ ‎（Ⅱ）若点P在x轴下方，当∠AOP=45°时，求抛物线的解析式；‎ ‎（Ⅲ）无论m取何值，该抛物线都经过定点H．当∠AHP=45°时，求抛物线的解析式．‎ ‎【解答】解：（Ⅰ）∵抛物线y=x2+mx﹣2m经过点A（1，0），‎ ‎∴0=1+m﹣2m，‎ 解得：m=1，‎ ‎∴抛物线解析式为y=x2+x﹣2，‎ ‎∵y=x2+x﹣2=（x+）2﹣，‎ ‎∴顶点P的坐标为（﹣，﹣）；‎ ‎（Ⅱ）抛物线y=x2+mx﹣2m的顶点P的坐标为（﹣，﹣），‎ 由点A（1，0）在x轴的正半轴上，点P在x轴的下方，∠AOP=45°知点P在第四象限，‎ 如图1，过点P作PQ⊥x轴于点Q，‎ 则∠POQ=∠OPQ=45°，‎ 可知PQ=OQ，即=﹣，‎ 解得：m1=0，m2=﹣10，‎ 当m=0时，点P不在第四象限，舍去；‎ ‎∴m=﹣10，‎ ‎∴抛物线的解析式为y=x2﹣10x+20；‎ ‎（Ⅲ）由y=x2+mx﹣2m=x2+m（x﹣2）可知当x=2时，无论m取何值时y都等于4，‎ ‎∴点H的坐标为（2，4），‎ 过点A作AD⊥AH，交射线HP于点D，分别过点D、H作x轴的垂线，垂足分别为E、G，‎ 则∠DEA=∠AGH=90°，‎ ‎∵∠DAH=90°，∠AHD=45°，‎ ‎∴∠ADH=45°，‎ ‎∴AH=AD，‎ ‎∵∠DAE+∠HAG=∠AHG+∠HAG=90°，‎ ‎∴∠DAE=∠AHG，‎ ‎∴△ADE≌△HAG，‎ ‎∴DE=AG=1、AE=HG=4，‎ 则点D的坐标为（﹣3，1）或（5，﹣1）；‎ ‎①当点D的坐标为（﹣3，1）时，可得直线DH的解析式为y=x+，‎ ‎∵点P（﹣，﹣）在直线y=x+上，‎ ‎∴﹣=×（﹣）+，‎ 解得：m1=﹣4、m2=﹣，‎ 当m=﹣4时，点P与点H重合，不符合题意，‎ ‎∴m=﹣；‎ ‎②当点D的坐标为（5，﹣1）时，可得直线DH的解析式为y=﹣x+，‎ ‎∵点P（﹣，﹣）在直线y=﹣x+上，‎ ‎∴﹣=﹣×（﹣）+，‎ 解得：m1=﹣4（舍），m2=﹣，‎ 综上，m=﹣或m=﹣，‎ 则抛物线的解析式为y=x2﹣x+或y=x2﹣x+．‎ ‎　‎ ‎20．如图所示，将二次函数y=x2+2x+1的图象沿x轴翻折，然后向右平移1个单位，再向上平移4个单位，得到二次函数y=ax2+bx+c的图象．函数y=x2+2x+1的图象的顶点为点A．函数y=ax2+bx+c的图象的顶点为点B，和x轴的交点为点C，D（点D位于点C的左侧）．‎ ‎（1）求函数y=ax2+bx+c的解析式；‎ ‎（2）从点A，C，D三个点中任取两个点和点B构造三角形，求构造的三角形是等腰三角形的概率；‎ ‎（3）若点M是线段BC上的动点，点N是△ABC三边上的动点，是否存在以AM为斜边的Rt△AMN，使△AMN的面积为△ABC面积的？若存在，求tan∠MAN的值；若不存在，请说明理由．‎ ‎【解答】解：（1）y=x2+2x+1=（x+1）2的图象沿x轴翻折，得y=﹣（x+1）2．‎ 把y=﹣（x+1）2向右平移1个单位，再向上平移4个单位，得y=﹣x2+4，‎ ‎∴所求的函数y=ax2+bx+c的解析式为y=﹣x2+4；‎ ‎（2）∵y=x2+2x+1=（x+1）2，‎ ‎∴A（﹣1，0），‎ 当y=0时，﹣x2+4=0，解得x=±2，则D（﹣2，0），C（2，0）；‎ 当x=0时，y=﹣x2+4=4，则B（0，4），‎ 从点A，C，D三个点中任取两个点和点B构造三角形的有：△ACB，△ADB，△CDB，‎ ‎∵AC=3，AD=1，CD=4，AB=，BC=2，BD=2，‎ ‎∴△BCD为等腰三角形，‎ ‎∴构造的三角形是等腰三角形的概率=；‎ ‎（3）存在．‎ 易得BC的解析是为y=﹣2x+4，S△ABC=AC•OB=×3×4=6，‎ M点的坐标为（m，﹣2m+4）（0≤m≤2），‎ ‎①当N点在AC上，如图1，‎ ‎∴△AMN的面积为△ABC面积的，‎ ‎∴（m+1）（﹣2m+4）=2，解得m1=0，m2=1，‎ 当m=0时，M点的坐标为（0，4），N（0，0），则AN=1，MN=4，‎ ‎∴tan∠MAC===4；‎ 当m=1时，M点的坐标为（1，2），N（1，0），则AN=2，MN=2，‎ ‎∴tan∠MAC===1；‎ ‎②当N点在BC上，如图2，‎ BC==2，‎ ‎∵BC•AN=AC•BC，解得AN==，‎ ‎∵S△AMN=AN•MN=2，‎ ‎∴MN==，‎ ‎∴∠MAC===；‎ ‎③当N点在AB上，如图3，作AH⊥BC于H，设AN=t，则BN=﹣t，‎ 由②得AH=，则BH==，‎ ‎∵∠NBG=∠HBA，‎ ‎∴△BNM∽△BHA，‎ ‎∴=，即=，‎ ‎∴MN=，‎ ‎∵AN•MN=2，‎ 即•（﹣t）•=2，‎ 整理得3t2﹣3t+14=0，△=（﹣3）2﹣4×3×14=﹣15＜0，方程没有实数解，‎ ‎∴点N在AB上不符合条件，‎ 综上所述，tan∠MAN的值为1或4或．‎ ‎　‎ ‎21．如图，已知抛物线y=ax2+bx+c（a≠0）经过点A（3，0），B（﹣1，0），C（0，﹣3）．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）若以点A为圆心的圆与直线BC相切于点M，求切点M的坐标；‎ ‎（3）若点Q在x轴上，点P在抛物线上，是否存在以点B，C，Q，P为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）把A（3，0），B（﹣1，0），C（0，﹣3）代入抛物线解析式得：，‎ 解得：，‎ 则该抛物线解析式为y=x2﹣2x﹣3；‎ ‎（2）设直线BC解析式为y=kx﹣3，‎ 把B（﹣1，0）代入得：﹣k﹣3=0，即k=﹣3，‎ ‎∴直线BC解析式为y=﹣3x﹣3，‎ ‎∴直线AM解析式为y=x+m，‎ 把A（3，0）代入得：1+m=0，即m=﹣1，‎ ‎∴直线AM解析式为y=x﹣1，‎ 联立得：，‎ 解得：，‎ 则M（﹣，﹣）；‎ ‎（3）存在以点B，C，Q，P为顶点的四边形是平行四边形，‎ 分三种情况考虑：‎ 设Q（x，0），P（m，m2﹣2m﹣3），‎ 当四边形BCQP为平行四边形时，由B（﹣1，0），C（0，﹣3），‎ 根据平移规律得：﹣1+x=0+m，0+0=﹣3+m2﹣2m﹣3，‎ 解得：m=1±，x=2±，‎ 当m=1+时，m2﹣2m﹣3=8+2﹣2﹣2﹣3=3，即P（1+，2）；‎ 当m=1﹣时，m2﹣2m﹣3=8﹣2﹣2+2﹣3=3，即P（1﹣，2）；‎ 当四边形BCPQ为平行四边形时，由B（﹣1，0），C（0，﹣3），‎ 根据平移规律得：﹣1+m=0+x，0+m2﹣2m﹣3=﹣3+0，‎ 解得：m=0或2，‎ 当m=0时，P（0，﹣3）（舍去）；当m=2时，P（2，﹣3），‎ 当四边形BQCP是平行四边形时，‎ 由平移规律得：﹣1+0=m+x，0﹣3=m2﹣2m﹣3，‎ 解得：m=0或2，x=﹣1或﹣3，‎ 当m=0时，P（0，﹣3）（舍去）；当m=2时，P（2，﹣3），‎ 综上，存在以点B，C，Q，P为顶点的四边形是平行四边形，P的坐标为（1+，3）或（1﹣，3）或（2，﹣3）．‎ ‎　‎ ‎22．已知顶点为A抛物线经过点，点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）如图1，直线AB与x轴相交于点M，y轴相交于点E，抛物线与y轴相交于点F，在直线AB上有一点P，若∠OPM=∠MAF，求△POE的面积；‎ ‎（3）如图2，点Q是折线A﹣B﹣C上一点，过点Q作QN∥y轴，过点E作EN∥x轴，直线QN与直线EN相交于点N，连接QE，将△QEN沿QE翻折得到△QEN1，若点N1落在x轴上，请直接写出Q点的坐标．‎ ‎【解答】解：（1）把点代入，‎ 解得：a=1，‎ ‎∴抛物线的解析式为：；‎ ‎（2）由知A（，﹣2），‎ 设直线AB解析式为：y=kx+b，代入点A，B的坐标，‎ 得：，‎ 解得：，‎ ‎∴直线AB的解析式为：y=﹣2x﹣1，‎ 易求E（0，1），，，‎ 若∠OPM=∠MAF，‎ ‎∴OP∥AF，‎ ‎∴△OPE∽△FAE，‎ ‎∴，‎ ‎∴，‎ 设点P（t，﹣2t﹣1），则：‎ 解得，，‎ 由对称性知；当时，也满足∠OPM=∠MAF，‎ ‎∴，都满足条件，‎ ‎∵△POE的面积=，‎ ‎∴△POE的面积为或．‎ ‎（3）若点Q在AB上运动，如图1，‎ 设Q（a，﹣2a﹣1），则NE=﹣a、QN=﹣2a，‎ 由翻折知QN′=QN=﹣2a、N′E=NE=﹣a，‎ 由∠QN′E=∠N=90°易知△QRN′∽△N′SE，‎ ‎∴==，即===2，‎ ‎∴QR=2、ES=，‎ 由NE+ES=NS=QR可得﹣a+=2，‎ 解得：a=﹣，‎ ‎∴Q（﹣，）；‎ 若点Q在BC上运动，且Q在y轴左侧，如图2，‎ 设NE=a，则N′E=a，‎ 易知RN′=2、SN′=1、QN′=QN=3，‎ ‎∴QR=、SE=﹣a，‎ 在Rt△SEN′中，（﹣a）2+12=a2，‎ 解得：a=，‎ ‎∴Q（﹣，2）；‎ 若点Q在BC上运动，且点Q在y轴右侧，如图3，‎ 设NE=a，则N′E=a，‎ 易知RN′=2、SN′=1、QN′=QN=3，‎ ‎∴QR=、SE=﹣a，‎ 在Rt△SEN′中，（﹣a）2+12=a2，‎ 解得：a=，‎ ‎∴Q（，2）．‎ 综上，点Q的坐标为（﹣，）或（﹣，2）或（，2）．‎ ‎　‎ ‎23．已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足：当x1＜x2＜0时，（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若MN与直线y=﹣2x平行，且M，N位于直线BC的两侧，y1＞y2，解决以下问题：‎ ‎①求证：BC平分∠MBN；‎ ‎②求△MBC外心的纵坐标的取值范围．‎ ‎【解答】解：（1）∵抛物线过点A（0，2），‎ ‎∴c=2，‎ 当x1＜x2＜0时，x1﹣x2＜0，由（x1﹣x2）（y1﹣y2）＞0，得到y1﹣y2＜0，‎ ‎∴当x＜0时，y随x的增大而增大，‎ 同理当x＞0时，y随x的增大而减小，‎ ‎∴抛物线的对称轴为y轴，且开口向下，即b=0，‎ ‎∵以O为圆心，OA为半径的圆与抛物线交于另两点B，C，如图1所示，‎ ‎∴△ABC为等腰三角形，‎ ‎∵△ABC中有一个角为60°，‎ ‎∴△ABC为等边三角形，且OC=OA=2，‎ 设线段BC与y轴的交点为点D，则有BD=CD，且∠OBD=30°，‎ ‎∴BD=OB•cos30°=，OD=OB•sin30°=1，‎ ‎∵B在C的左侧，‎ ‎∴B的坐标为（﹣，﹣1），‎ ‎∵B点在抛物线上，且c=2，b=0，‎ ‎∴3a+2=﹣1，‎ 解得：a=﹣1，‎ 则抛物线解析式为y=﹣x2+2；‎ ‎（2）①由（1）知，点M（x1，﹣x12+2），N（x2，﹣x22+2），‎ ‎∵MN与直线y=﹣2x平行，‎ ‎∴设直线MN的解析式为y=﹣2x+m，则有﹣x12+2=﹣2x1+m，即m=﹣x12+2x1+2，‎ ‎∴直线MN解析式为y=﹣2x﹣x12+2x1+2，‎ 把y=﹣2x﹣x12+2x1+2代入y=﹣x2+2，解得：x=x1或x=2﹣x1，‎ ‎∴x2=2﹣x1，即y2=﹣（2﹣x1）2+2=﹣x12+4x1﹣10，‎ 作ME⊥BC，NF⊥BC，垂足为E，F，如图2所示，‎ ‎∵M，N位于直线BC的两侧，且y1＞y2，则y2＜﹣1＜y1≤2，且﹣＜x1＜x2，‎ ‎∴ME=y1﹣（﹣1）=﹣x12+3，BE=x1﹣（﹣）=x1+，NF=﹣1﹣y2=x12﹣4x1+9，BF=x2﹣（﹣）=3﹣x1，‎ 在Rt△BEM中，tan∠MBE===﹣x1，‎ 在Rt△BFN中，tan∠NBF=====﹣x1，‎ ‎∵tan∠MBE=tan∠NBF，‎ ‎∴∠MBE=∠NBF，‎ 则BC平分∠MBN；‎ ‎②∵y轴为BC的垂直平分线，‎ ‎∴设△MBC的外心为P（0，y0），则PB=PM，即PB2=PM2，‎ 根据勾股定理得：3+（y0+1）2=x12+（y0﹣y1）2，‎ ‎∵x12=2﹣y1，‎ ‎∴y02+2y0+4=（2﹣y1）+（y0﹣y1）2，即y0=y1﹣1，‎ 由①得：﹣1＜y1≤2，‎ ‎∴﹣＜y0≤0，‎ 则△MBC的外心的纵坐标的取值范围是﹣＜y0≤0．‎ ‎　‎ ‎24．如图，已知二次函数的图象过点O（0，0）．A（8，4），与x轴交于另一点B，且对称轴是直线x=3．‎ ‎（1）求该二次函数的解析式；‎ ‎（2）若M是OB上的一点，作MN∥AB交OA于N，当△ANM面积最大时，求M的坐标；‎ ‎（3）P是x轴上的点，过P作PQ⊥x轴与抛物线交于Q．过A作AC⊥x轴于C，当以O，P，Q为顶点的三角形与以O，A，C为顶点的三角形相似时，求P点的坐标．‎ ‎【解答】解：（1）∵抛物线过原点，对称轴是直线x=3，‎ ‎∴B点坐标为（6，0），‎ 设抛物线解析式为y=ax（x﹣6），‎ 把A（8，4）代入得a•8•2=4，解得a=，‎ ‎∴抛物线解析式为y=x（x﹣6），即y=x2﹣x；‎ ‎（2）设M（t，0），‎ 易得直线OA的解析式为y=x，‎ 设直线AB的解析式为y=kx+b，‎ 把B（6，0），A（8，4）代入得，解得，‎ ‎∴直线AB的解析式为y=2x﹣12，‎ ‎∵MN∥AB，‎ ‎∴设直线MN的解析式为y=2x+n，‎ 把M（t，0）代入得2t+n=0，解得n=﹣2t，‎ ‎∴直线MN的解析式为y=2x﹣2t，‎ 解方程组得，则N（t，t），‎ ‎∴S△AMN=S△AOM﹣S△NOM ‎=•4•t﹣•t•t ‎=﹣t2+2t ‎=﹣（t﹣3）2+3，‎ 当t=3时，S△AMN有最大值3，此时M点坐标为（3，0）；‎ ‎（3）设Q（m，m2﹣m），‎ ‎∵∠OPQ=∠ACO，‎ ‎∴当=时，△PQO∽△COA，即=，‎ ‎∴PQ=2PO，即|m2﹣m|=2|m|，‎ 解方程m2﹣m=2m得m1=0（舍去），m2=14，此时P点坐标为（14，0）；‎ 解方程m2﹣m=﹣2m得m1=0（舍去），m2=﹣2，此时P点坐标为（﹣2，0）；‎ ‎∴当=时，△PQO∽△CAO，即=，‎ ‎∴PQ=PO，即|m2﹣m|=|m|，‎ 解方程m2﹣m=m得m1=0（舍去），m2=8（舍去），‎ 解方程m2﹣m=﹣m得m1=0（舍去），m2=4，此时P点坐标为（4，0）；‎ 综上所述，P点坐标为（14，0）或（﹣2，0）或（4，0）．‎ ‎　‎ ‎25．如图，抛物线y=ax2+bx+c与两坐标轴相交于点A（﹣1，0）、B（3，0）、C（0，3），D是抛物线的顶点，E是线段AB的中点．‎ ‎（1）求抛物线的解析式，并写出D点的坐标；‎ ‎（2）F（x，y）是抛物线上的动点：‎ ‎①当x＞1，y＞0时，求△BDF的面积的最大值；‎ ‎②当∠AEF=∠DBE时，求点F的坐标．‎ ‎【解答】解：（1）将A（﹣1，0）、B（3，0）、C（0，3）代入y=ax2+bx+c，‎ ‎，解得：，‎ ‎∴抛物线的解析式为y=﹣x2+2x+3．‎ ‎∵y=﹣x2+2x+3=﹣（x﹣1）2+4，‎ ‎∴顶点D的坐标为（1，4）．‎ ‎（2）①过点F作FM∥y轴，交BD于点M，如图1所示．‎ 设直线BD的解析式为y=mx+n（m≠0），‎ 将（3，0）、（1，4）代入y=mx+n，‎ ‎，解得：，‎ ‎∴直线BD的解析式为y=﹣2x+6．‎ ‎∵点F的坐标为（x，﹣x2+2x+3），‎ ‎∴点M的坐标为（x，﹣2x+6），‎ ‎∴FM=﹣x2+2x+3﹣（﹣2x+6）=﹣x2+4x﹣3，‎ ‎∴S△BDF=FM•（yB﹣yD）=﹣x2+4x﹣3=﹣（x﹣2）2+1．‎ ‎∵﹣1＜0，‎ ‎∴当x=2时，S△BDF取最大值，最大值为1．‎ ‎②过点E作EN∥BD交y轴于点N，交抛物线于点F1‎ ‎，在y轴负半轴取ON′=ON，连接EN′，射线EN′交抛物线于点F2，如图2所示．‎ ‎∵EF1∥BD，‎ ‎∴∠AEF1=∠DBE．‎ ‎∵ON=ON′，EO⊥NN′，‎ ‎∴∠AEF2=∠AEF1=∠DBE．‎ ‎∵E是线段AB的中点，A（﹣1，0），B（3，0），‎ ‎∴点E的坐标为（1，0）．‎ 设直线EF1的解析式为y=﹣2x+b1，‎ 将E（1，0）代入y=﹣2x+b1，‎ ‎﹣2+b1=0，解得：b1=2，‎ ‎∴直线EF1的解析式为y=﹣2x+2．‎ 联立直线EF1、抛物线解析式成方程组，，‎ 解得：，（舍去），‎ ‎∴点F1的坐标为（2﹣，2﹣2）．‎ 当x=0时，y=﹣2x+2=2，‎ ‎∴点N的坐标为（0，2），‎ ‎∴点N′的坐标为（0，﹣2）．‎ 同理，利用待定系数法可求出直线EF2的解析式为y=2x﹣2．‎ 联立直线EF2、抛物线解析式成方程组，，‎ 解得：，（舍去），‎ ‎∴点F2的坐标为（﹣，﹣2﹣2）．‎ 综上所述：当∠AEF=∠DBE时，点F的坐标为（2﹣，2﹣2）或（﹣，﹣2‎ ‎﹣2）．‎ ‎　‎ ‎26．如图1，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+bx+3交x轴于B、C两点（点B在左，点C在右），交y轴于点A，且OA=OC，B（﹣1，0）．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）如图2，点D为抛物线的顶点，连接CD，点P是抛物线上一动点，且在C、D两点之间运动，过点P作PE∥y轴交线段CD于点E，设点P的横坐标为t，线段PE长为d，写出d与t的关系式（不要求写出自变量t的取值范围）；‎ ‎（3）如图3，在（2）的条件下，连接BD，在BD上有一动点Q，且DQ=CE，连接EQ，当∠BQE+∠DEQ=90°时，求此时点P的坐标．‎ ‎【解答】解：（1）当x=0时，y=3，‎ ‎∴A（0，3）即OA=3，‎ ‎∵OA=OC，‎ ‎∴OC=3，‎ ‎∴C（3，0），‎ ‎∵抛物线y=ax2+bx+3经过点B（﹣1，0），C（3，0）‎ ‎∴，‎ 解得：，‎ ‎∴抛物线的解析式为：y=﹣x2+2x+3；‎ ‎（2）如图1，延长PE交x轴于点H，‎ ‎∵y=﹣x2+2x+3=﹣（x﹣1）2+4，‎ ‎∴D（1，4），‎ 设直线CD的解析式为y=kx+b，‎ 将点C（3，0）、D（1，4）代入，得：‎ ‎，‎ 解得：，‎ ‎∴y=﹣2x+6，‎ ‎∴E（t，﹣2t+6），P（t，﹣t2+2t+3），‎ ‎∴PH=﹣t2+2t+3，EH=﹣2t+6，‎ ‎∴d=PH﹣EH=﹣t2+2t+3﹣（﹣2t+6）=﹣t2+4t﹣3；‎ ‎（3）如图2，作DK⊥OC于点K，作QM∥x轴交DK于点T，延长PE、EP交OC于H、交QM于M，作ER⊥DK于点R，记QE与DK的交点为N，‎ ‎∵D（1，4），B（﹣1，0），C（3，0），‎ ‎∴BK=2，KC=2，‎ ‎∴DK垂直平分BC，‎ ‎∴BD=CD，‎ ‎∴∠BDK=∠CDK，‎ ‎∵∠BQE=∠QDE+∠DEQ，∠BQE+∠DEQ=90°，‎ ‎∴∠QDE+∠DEQ+∠DEQ=90°，即2∠CDK+2∠DEQ=90°，‎ ‎∴∠CDK+∠DEQ=45°，即∠RNE=45°，‎ ‎∵ER⊥DK，‎ ‎∴∠NER=45°，‎ ‎∴∠MEQ=∠MQE=45°，‎ ‎∴QM=ME，‎ ‎∵DQ=CE，∠DTQ=∠EHC、∠QDT=∠CEH，‎ ‎∴△DQT≌△ECH，‎ ‎∴DT=EH，QT=CH，‎ ‎∴ME=4﹣2（﹣2t+6），‎ QM=MT+QT=MT+CH=t﹣1+（3﹣t），‎ ‎4﹣2（﹣2t+6）=t﹣1+（3﹣t），‎ 解得：t=，‎ ‎∴P（，）．‎ ‎　‎ ‎27．已知抛物线F：y=x2+bx+c的图象经过坐标原点O，且与x轴另一交点为（﹣，0）．‎ ‎（1）求抛物线F的解析式；‎ ‎（2）如图1，直线l：y=x+m（m＞0）与抛物线F相交于点A（x1，y1）和点B（x2，y2）（点A在第二象限），求y2﹣y1的值（用含m的式子表示）；‎ ‎（3）在（2）中，若m=，设点A′是点A关于原点O的对称点，如图2．‎ ‎①判断△AA′B的形状，并说明理由；‎ ‎②平面内是否存在点P，使得以点A、B、A′、P为顶点的四边形是菱形？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）∵抛物线y=x2+bx+c的图象经过点（0，0）和（﹣，0），‎ ‎∴，解得：，‎ ‎∴抛物线F的解析式为y=x2+x．‎ ‎（2）将y=x+m代入y=x2+x，得：x2=m，‎ 解得：x1=﹣，x2=，‎ ‎∴y1=﹣+m，y2=+m，‎ ‎∴y2﹣y1=（+m）﹣（﹣+m）=（m＞0）．‎ ‎（3）∵m=，‎ ‎∴点A的坐标为（﹣，），点B的坐标为（，2）．‎ ‎∵点A′是点A关于原点O的对称点，‎ ‎∴点A′的坐标为（，﹣）．‎ ‎①△AA′B为等边三角形，理由如下：‎ ‎∵A（﹣，），B（，2），A′（，﹣），‎ ‎∴AA′=，AB=，A′B=，‎ ‎∴AA′=AB=A′B，‎ ‎∴△AA′B为等边三角形．‎ ‎②∵△AA′B为等边三角形，‎ ‎∴存在符合题意的点P，且以点A、B、A′、P为顶点的菱形分三种情况，设点P的坐标为（x，y）．‎ ‎（i）当A′B为对角线时，有，‎ 解得：，‎ ‎∴点P的坐标为（2，）；‎ ‎（ii）当AB为对角线时，有，‎ 解得：，‎ ‎∴点P的坐标为（﹣，）；‎ ‎（iii）当AA′为对角线时，有，‎ 解得：，‎ ‎∴点P的坐标为（﹣，﹣2）．‎ 综上所述：平面内存在点P，使得以点A、B、A′、P为顶点的四边形是菱形，点P的坐标为（2，）、（﹣，）和（﹣，﹣2）．‎ ‎　‎ ‎28．已知：如图，一次函数y=kx﹣1的图象经过点A（3，m）（m＞0），与y轴交于点B．点C在线段AB上，且BC=2AC，过点C作x轴的垂线，垂足为点D．若AC=CD．‎ ‎（1）求这个一次函数的表达式；‎ ‎（2）已知一开口向下、以直线CD为对称轴的抛物线经过点A，它的顶点为P，若过点P且垂直于AP的直线与x轴的交点为Q（﹣，0），求这条抛物线的函数表达式．‎ ‎【解答】解：（1）过点A作AF⊥x轴，过点B作BF⊥‎ CD于H，交AF于点F，过点C作CE⊥AF于点E 设AC=n，则CD=n ‎∵点B坐标为（0，﹣1）‎ ‎∴CH=n+1，AF=m+1‎ ‎∵CH∥AF，BC=2AC ‎∴‎ 即：‎ 整理得：‎ n=‎ Rt△AEC中，‎ CE2+AE2=AC2‎ ‎∴5+（m﹣n）2=n2‎ 把n=代入 ‎5+（m﹣）2=（）2‎ 解得m1=5，m2=﹣3（舍去）‎ ‎∴n=3‎ ‎∴把A（3，5）代入y=kx﹣1得 k=‎ ‎∴y=x﹣1‎ ‎（2）如图，过点A作AE⊥CD于点E 设点P坐标为（2，n），由已知n＞0‎ 由已知，PD⊥x轴 ‎∴△PQD∽△APE ‎∴‎ ‎∴‎ 解得n1=7，n2=﹣2（舍去）‎ 设抛物线解析式为y=a（x﹣h）2+k ‎∴y=a（x﹣2）2+7‎ 把A（3，5）代入y=a（x﹣2）2+7‎ 解得a=﹣‎ ‎∴抛物线解析式为：y=﹣‎ ‎　‎ ‎29．如图，已知抛物线y=ax2+bx（a≠0）过点A（，﹣3）和点B（3，0）．过点A作直线AC∥x轴，交y轴于点C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上取一点P，过点P作直线AC的垂线，垂足为D．连接OA，使得以A，D，P为顶点的三角形与△AOC相似，求出对应点P的坐标；‎ ‎（3）抛物线上是否存在点Q，使得S△AOC=S△AOQ？若存在，求出点Q的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）把A（，﹣3）和点B（3，0）代入抛物线得：，‎ 解得：a=，b=﹣，‎ 则抛物线解析式为y=x2﹣x；‎ ‎（2）当P在直线AD上方时，‎ 设P坐标为（x，x2﹣x），则有AD=x﹣，PD=x2﹣x+3，‎ 当△OCA∽△ADP时，=，即=，‎ 整理得：3x2﹣9x+18=2x﹣6，即3x2﹣11x+24=0，‎ 解得：x=，即x=或x=（舍去）‎ 此时P（，﹣）；‎ 当△OCA∽△PDA时，=，即=，‎ 整理得：x2﹣9x+6=6x﹣6，即x2﹣5x+12=0，‎ 解得：x=，即x=4或（舍去），‎ 此时P（4，6）；‎ 当P在直线AD下方时，同理可得：P的坐标为（0，0）或（，﹣），‎ 综上，P的坐标为（，﹣）或（4，6）（0，0）或（，﹣）；‎ ‎（3）在Rt△AOC中，OC=3，AC=，‎ 根据勾股定理得：OA=2，‎ ‎∵OC•AC=OA•h，‎ ‎∴h=，‎ ‎∵S△AOC=S△AOQ=，‎ ‎∴△AOQ边OA上的高为，‎ 过O作OM⊥OA，截取OM=，过M作MN∥OA，交y轴于点N，如图所示：‎ 在Rt△OMN中，ON=2OM=9，即N（0，9），‎ 过M作MH⊥x轴，‎ 在Rt△OMH中，MH=OM=，OH=OM=，即M（，），‎ 设直线MN解析式为y=kx+9，‎ 把M坐标代入得：=k+9，即k=﹣，即y=﹣x+9，‎ 联立得：，‎ 解得：或，即Q（3，0）或（﹣2，15），‎ 则抛物线上存在点Q，使得S△AOC=S△AOQ，此时点Q的坐标为（3，0）或（﹣2，15）．‎ ‎　‎ ‎30．如图1，抛物线C1：y=ax2﹣2ax+c（a＜0）与x轴交于A、B两点，与y轴交于点C．已知点A的坐标为（﹣1，0），点O为坐标原点，OC=3OA，抛物线C1‎ 的顶点为G．‎ ‎（1）求出抛物线C1的解析式，并写出点G的坐标；‎ ‎（2）如图2，将抛物线C1向下平移k（k＞0）个单位，得到抛物线C2，设C2与x轴的交点为A′、B′，顶点为G′，当△A′B′G′是等边三角形时，求k的值：‎ ‎（3）在（2）的条件下，如图3，设点M为x轴正半轴上一动点，过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点，试探究在直线y=﹣1上是否存在点N，使得以P、Q、N为顶点的三角形与△AOQ全等，若存在，直接写出点M，N的坐标：若不存在，请说明理由．‎ ‎【解答】解：（1）∵点A的坐标为（﹣1，0），‎ ‎∴OA=1，‎ ‎∴OC=3OA，‎ ‎∴点C的坐标为（0，3），‎ 将A、C坐标代入y=ax2﹣2ax+c，得：‎ ‎，‎ 解得：，‎ ‎∴抛物线C1的解析式为y=﹣x2+2x+3=﹣（x﹣1）2+4，‎ 所以点G的坐标为（1，4）．‎ ‎（2）设抛物线C2的解析式为y=﹣x2+2x+3﹣k，即y=﹣（x﹣1）2+4﹣k，‎ 过点G′作G′D⊥x轴于点D，设BD′=m，‎ ‎∵△A′B′G′为等边三角形，‎ ‎∴G′D=B′D=m，‎ 则点B′的坐标为（m+1，0），点G′的坐标为（1，m），‎ 将点B′、G′的坐标代入y=﹣（x﹣1）2+4﹣k，得：‎ ‎，‎ 解得：（舍），，‎ ‎∴k=1；‎ ‎（3）设M（x，0），则P（x，﹣x2+2x+3）、Q（x，﹣x2+2x+2），‎ ‎∴PQ=OA=1，‎ ‎∵∠AOQ、∠PQN均为钝角，‎ ‎∴△AOQ≌△PQN，‎ 如图2，延长PQ交直线y=﹣1于点H，‎ 则∠QHN=∠OMQ=90°，‎ 又∵△AOQ≌△PQN，‎ ‎∴OQ=QN，∠AOQ=∠PQN，‎ ‎∴∠MOQ=∠HQN，‎ ‎∴△OQM≌△QNH（AAS），‎ ‎∴OM=QH，即x=﹣x2+2x+2+1，‎ 解得：x=（负值舍去），‎ 当x=时，HN=QM=﹣x2+2x+2=，点M（，0），‎ ‎∴点N坐标为（+，﹣1），即（，﹣1）；‎ 或（﹣，﹣1），即（1，﹣1）；‎ 如图3，‎ 同理可得△OQM≌△PNH，‎ ‎∴OM=PH，即x=﹣（﹣x2+2x+2）﹣1，‎ 解得：x=﹣1（舍）或x=4，‎ 当x=4时，点M的坐标为（4，0），HN=QM=﹣（﹣x2+2x+2）=6，‎ ‎∴点N的坐标为（4+6，﹣1）即（10，﹣1），或（4﹣6，﹣1）即（﹣2，﹣1）；‎ 综上点M1（，0）、N1（，﹣1）；M2（，0）、N2（1，﹣1）；‎ M3（4，0）、N3（10，﹣1）；M4（4，0）、N4（﹣2，﹣1）．‎ ‎　‎ ‎31．在平面直角坐标系中，二次函数y=ax2+x+c的图象经过点C（0，2）和点D（4，﹣2）．点E是直线y=﹣x+2与二次函数图象在第一象限内的交点．‎ ‎（1）求二次函数的解析式及点E的坐标．‎ ‎（2）如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．‎ ‎（3）如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．‎ ‎【解答】解：（1）把C（0，2），D（4，﹣2）代入二次函数解析式得：，‎ 解得：，即二次函数解析式为y=﹣x2+x+2，‎ 联立一次函数解析式得：，‎ 消去y得：﹣x+2=﹣x2+x+2，‎ 解得：x=0或x=3，‎ 则E（3，1）；‎ ‎（2）如图①，过M作MH∥y轴，交CE于点H，‎ 设M（m，﹣m2+m+2），则H（m，﹣m+2），‎ ‎∴MH=（﹣m2+m+2）﹣（﹣m+2）=﹣m2+2m，‎ S四边形COEM=S△OCE+S△CME=×2×3+MH•3=﹣m2+3m+3，‎ 当m=﹣=时，S最大=，此时M坐标为（，3）；‎ ‎（3）连接BF，如图②所示，‎ 当﹣x2+x+20=0时，x1=，x2=，‎ ‎∴OA=，OB=，‎ ‎∵∠ACO=∠ABF，∠AOC=∠FOB，‎ ‎∴△AOC∽△FOB，‎ ‎∴=，即=，‎ 解得：OF=，‎ 则F坐标为（0，﹣）．‎ ‎　‎ ‎32．如图，已知顶点为C（0，﹣3）的抛物线y=ax2+b（a≠0）与x轴交于A，B两点，直线y=x+m过顶点C和点B．‎ ‎（1）求m的值；‎ ‎（2）求函数y=ax2+b（a≠0）的解析式；‎ ‎（3）抛物线上是否存在点M，使得∠MCB=15°？若存在，求出点M的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）将（0，﹣3）代入y=x+m，‎ 可得：m=﹣3；‎ ‎（2）将y=0代入y=x﹣3得：x=3，‎ 所以点B的坐标为（3，0），‎ 将（0，﹣3）、（3，0）代入y=ax2+b中，‎ 可得：，‎ 解得：，‎ 所以二次函数的解析式为：y=x2﹣3；‎ ‎（3）存在，分以下两种情况：‎ ‎①若M在B上方，设MC交x轴于点D，则∠ODC=45°+15°=60°，‎ ‎∴OD=OC•tan30°=，‎ 设DC为y=kx﹣3，代入（，0），可得：k=，‎ 联立两个方程可得：，‎ 解得：，‎ 所以M1（3，6）；‎ ‎②若M在B下方，设MC交x轴于点E，则∠OEC=45°﹣15°=30°，‎ ‎∴OE=OC•tan60°=3，‎ 设EC为y=kx﹣3，代入（3，0）可得：k=，‎ 联立两个方程可得：，‎ 解得：，‎ 所以M2（，﹣2），‎ 综上所述M的坐标为（3，6）或（，﹣2）．‎ ‎　‎ ‎33．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．‎ ‎（1）求抛物线的解析式和直线AC的解析式；‎ ‎（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；‎ ‎（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）设抛物线解析式为y=a（x+1）（x﹣3），‎ 即y=ax2﹣2ax﹣3a，‎ ‎∴﹣2a=2，解得a=﹣1，‎ ‎∴抛物线解析式为y=﹣x2+2x+3；‎ 当x=0时，y=﹣x2+2x+3=3，则C（0，3），‎ 设直线AC的解析式为y=px+q，‎ 把A（﹣1，0），C（0，3）代入得，解得，‎ ‎∴直线AC的解析式为y=3x+3；‎ ‎（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，‎ ‎∴顶点D的坐标为（1，4），‎ 作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（﹣3，0），‎ ‎∵MB=MB′，‎ ‎∴MB+MD=MB′+MD=DB′，此时MB+MD的值最小，‎ 而BD的值不变，‎ ‎∴此时△BDM的周长最小，‎ 易得直线DB′的解析式为y=x+3，‎ 当x=0时，y=x+3=3，‎ ‎∴点M的坐标为（0，3）；‎ ‎（3）存在．‎ 过点C作AC的垂线交抛物线于另一点P，如图2，‎ ‎∵直线AC的解析式为y=3x+3，‎ ‎∴直线PC的解析式可设为y=﹣x+b，‎ 把C（0，3）代入得b=3，‎ ‎∴直线PC的解析式为y=﹣x+3，‎ 解方程组，解得或，则此时P点坐标为（，）；‎ 过点A作AC的垂线交抛物线于另一点P，直线PC的解析式可设为y=﹣x+b，‎ 把A（﹣1，0）代入得+b=0，解得b=﹣，‎ ‎∴直线PC的解析式为y=﹣x﹣，‎ 解方程组，解得或，则此时P点坐标为（，﹣），‎ 综上所述，符合条件的点P的坐标为（，）或（，﹣），‎ ‎　‎ ‎34．已知抛物线y=a（x﹣1）2过点（3，1），D为抛物线的顶点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若点B、C均在抛物线上，其中点B（0，），且∠BDC=90°，求点C的坐标；‎ ‎（3）如图，直线y=kx+4﹣k与抛物线交于P、Q两点．‎ ‎①求证：∠PDQ=90°；‎ ‎②求△PDQ面积的最小值．‎ ‎【解答】解：（1）将点（3，1）代入解析式，得：4a=1，‎ 解得：a=，‎ 所以抛物线解析式为y=（x﹣1）2；‎ ‎（2）由（1）知点D坐标为（1，0），‎ 设点C的坐标为（x0，y0），（x0＞1、y0＞0），‎ 则y0=（x0﹣1）2，‎ 如图1，过点C作CF⊥x轴，‎ ‎∴∠BOD=∠DFC=90°、∠DCF+∠CDF=90°，‎ ‎∵∠BDC=90°，‎ ‎∴∠BDO+∠CDF=90°，‎ ‎∴∠BDO=∠DCF，‎ ‎∴△BDO∽△DCF，‎ ‎∴=，‎ ‎∴==，‎ 解得：x0=17，此时y0=64，‎ ‎∴点C的坐标为（17，64）．‎ ‎（3）①证明：设点P的坐标为（x1，y1），点Q为（x2，y2），（其中x1＜1＜x2，y1＞0，y2＞0），‎ 由，得：x2﹣（4k+2）x+4k﹣15=0，‎ ‎∴，‎ ‎∴（x1﹣1）（x2﹣1）=﹣16，‎ 如图2，分别过点P、Q作x轴的垂线，垂足分别为M、N，‎ 则PM=y1=（x1﹣1）2，QN=y2=（x2﹣1）2，‎ DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1，‎ ‎∴PM•QN=DM•DN=16，‎ ‎∴=，‎ 又∠PMD=∠DNQ=90°，‎ ‎∴△PMD∽△DNQ，‎ ‎∴∠MPD=∠NDQ，‎ 而∠MPD+∠MDP=90°，‎ ‎∴∠MDP+∠NDQ=90°，即∠PDQ=90°；‎ ‎②过点D作x轴的垂线交直线PQ于点G，则点G的坐标为（1，4），‎ 所以DG=4，‎ ‎∴S△PDQ=DG•MN=×4×|x1﹣x2|=2=8，‎ ‎∴当k=0时，S△PDQ取得最小值16．‎ ‎　‎ ‎35．抛物线y=﹣x2+x﹣1与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，其顶点为D．将抛物线位于直线l：y=t（t＜）上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．‎ ‎（1）点A，B，D的坐标分别为　（，0）　，　（3，0）　，　（，）　；‎ ‎（2）如图①，抛物线翻折后，点D落在点E处．当点E在△ABC内（含边界）时，求t的取值范围；‎ ‎（3）如图②，当t=0时，若Q是“M”形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）当y=0时，有﹣x2+x﹣1=0，‎ 解得：x1=，x2=3，‎ ‎∴点A的坐标为（，0），点B的坐标为（3，0）．‎ ‎∵y=﹣x2+x﹣1=﹣（x2﹣x）﹣1=﹣（x﹣）2+，‎ ‎∴点D的坐标为（，）．‎ 故答案为：（，0）；（3，0）；（，）．‎ ‎（2）∵点E、点D关于直线y=t对称，‎ ‎∴点E的坐标为（，2t﹣）．‎ 当x=0时，y=﹣x2+x﹣1=﹣1，‎ ‎∴点C的坐标为（0，﹣1）．‎ 设线段BC所在直线的解析式为y=kx+b，‎ 将B（3，0）、C（0，﹣1）代入y=kx+b，‎ ‎，解得：，‎ ‎∴线段BC所在直线的解析式为y=x﹣1．‎ ‎∵点E在△ABC内（含边界），‎ ‎∴，‎ 解得：≤t≤．‎ ‎（3）当x＜或x＞3时，y=﹣x2+x﹣1；‎ 当≤x≤3时，y=x2﹣x+1．‎ 假设存在，设点P的坐标为（m，0），则点Q的横坐标为m．‎ ‎①当m＜或m＞3时，点Q的坐标为（m，﹣x2+x﹣1）（如图1），‎ ‎∵以CQ为直径的圆与x轴相切于点P，‎ ‎∴CP⊥PQ，‎ ‎∴CQ2=CP2+PQ2，即m2+（﹣m2+m）2=m2+1+m2+（﹣m2+m﹣1）2，‎ 整理，得：m1=，m2=，‎ ‎∴点P的坐标为（，0）或（，0）；‎ ‎②当≤m≤3时，点Q的坐标为（m，x2﹣x+1）（如图2），‎ ‎∵以CQ为直径的圆与x轴相切于点P，‎ ‎∴CP⊥PQ，‎ ‎∴CQ2=CP2+PQ2，即m2+（m2﹣m+2）2=m2+1+m2+（m2﹣m+1）2，‎ 整理，得：11m2﹣28m+12=0，‎ 解得：m3=，m4=2，‎ ‎∴点P的坐标为（，0）或（1，0）．‎ 综上所述：存在以CQ为直径的圆与x轴相切于点P，点P的坐标为（，0）、（，0）、（1，0）或（，0）．‎ ‎　‎ ‎36．如图，抛物线y=ax2+4x+c（a≠0）经过点A（﹣1，0），点E（4，5），与y轴交于点B，连接AB．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）将△ABO绕点O旋转，点B的对应点为点F．‎ ‎①当点F落在直线AE上时，求点F的坐标和△ABF的面积；‎ ‎②当点F到直线AE的距离为 时，过点F作直线AE的平行线与抛物线相交，请直接写出交点的坐标．‎ ‎【解答】解：（1）将A，E点坐标代入函数解析式，得 ‎，‎ 解得，‎ 抛物线的解析式是y=﹣x2+4x+5，‎ ‎（2）设AE的解析式为y=kx+b，将A，E点坐标代入，得 ‎，‎ 解得，‎ AE的解析式为y=x+1，‎ x=0时，y=1即C（0，1），‎ 设F点坐标为（n，n+1），‎ 由旋转的性质得，OF=OB=5，‎ n2+（n+1）2=25，解得n1=﹣4，n2=3，‎ F（﹣4，﹣3），F（3，4），‎ 当F（﹣4，﹣3）时如图1，‎ S△ABF=S△BCF﹣S△ABC=BC•|xF|﹣BC•|xA|=BC•（xA﹣xF）‎ S△ABF=×4（﹣1+4）=6；‎ 当F（3，4）时，如图2，‎ S△ABF=S△BCF+S△ABC=BC•|xF|+BC•|xA|=BC•（xF﹣xA）‎ S△ABF=×4（3+1）=8；‎ ‎（3）如图3，‎ ‎∵∠HCG=∠ACO，∠HGC=∠COA，‎ ‎∴△HGC∽△COA，‎ ‎∵OA=OC=1，∴CG=HG=，‎ 由勾股定理，得 HC==2，‎ 直线AE向上平移2个单位或向下平移2个单位，‎ l的解析是为y=x+3，l1的解析是为y=x﹣1，‎ 联立解得x1=，x2=，‎ ‎，解得x3=，x4=，‎ F点的坐标为（，），（，），（，‎ ‎），（，）．‎ ‎　‎ ‎37．如图，在平面直角坐标系中，二次函数y=（x﹣a）（x﹣3）（0＜a＜3）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点D，过其顶点C作直线CP⊥x轴，垂足为点P，连接AD、BC．‎ ‎（1）求点A、B、D的坐标；‎ ‎（2）若△AOD与△BPC相似，求a的值；‎ ‎（3）点D、O、C、B能否在同一个圆上？若能，求出a的值；若不能，请说明理由．‎ ‎【解答】解：（1）∵y=（x﹣a）（x﹣3）（0＜a＜3），‎ ‎∴A（a，0），B（3，0）．‎ 当x=0时，y=3a，‎ ‎∴D（0，3a）；‎ ‎（2）∵A（a，0），B（3，0），‎ ‎∴对称轴直线方程为：x=．‎ 当x=时，y=﹣（）2，‎ ‎∴C（，﹣（）2），‎ PB=3﹣，PC=（）2，‎ ‎①若△AOD∽△BPC时，则=，即=，‎ 解得a=±3（舍去）；‎ ‎②若△AOD∽△CPB时，则=，即=，‎ 解得a=3（舍去）或a=．‎ 所以a的值是．‎ ‎（3）能．理由如下：‎ 联结BD，取中点M ‎∵D、O、B在同一个圆上，且圆心M为（，a）．‎ 若点C也在圆上，则MC=MB．即（﹣）2+（a+（）2）2=（﹣3）2+（a﹣0）2，‎ 整理，得 a4﹣14a2+45=0，‎ 所以（a2﹣5）（a2﹣9）=0，‎ 解得a1=，a2=﹣（舍），a3=3（舍），a4=﹣3（舍），‎ ‎∴a=．‎ ‎　‎ ‎38．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于原点及点A，且经过点B（4，8），对称轴为直线x=﹣2．‎ ‎（1）求抛物线的解析式；‎ ‎（2）设直线y=kx+4与抛物线两交点的横坐标分别为x1，x2（x1＜x2），当时，求k的值；‎ ‎（3）连接OB，点P为x轴下方抛物线上一动点，过点P作OB的平行线交直线AB于点Q，当S△POQ：S△BOQ=1：2时，求出点P的坐标．‎ ‎（坐标平面内两点M（x1，y1），N（x2，y2）之间的距离MN=）‎ ‎【解答】解：（1）根据题意得，，‎ ‎∴，‎ ‎∴抛物线解析式为y=x2+x；‎ ‎（2）∵直线y=kx+4与抛物线两交点的横坐标分别为x1，x2，‎ ‎∴x2+x=kx+4，‎ ‎∴x2﹣4（k﹣1）x﹣16=0，‎ 根据根与系数的关系得，x1+x2=4（k﹣1），x1x2=﹣16，‎ ‎∵，‎ ‎∴2（x1﹣x2）=x1x2，‎ ‎∴4（x1﹣x2）2=（x1x2）2，‎ ‎∴4[（x1+x2）2﹣4x1x2]=（x1x2）2，‎ ‎∴4[16（k﹣1）2+64]=162，‎ ‎∴k=1；‎ ‎（3）如图，取OB的中点C，‎ ‎∴BC=OB，‎ ‎∵B（4，8），‎ ‎∴C（2，4），‎ ‎∵PQ∥OB，‎ ‎∴点O到PQ的距离等于点O到OB的距离，‎ ‎∵S△POQ：S△BOQ=1：2，‎ ‎∴OB=2PQ，‎ ‎∴PQ=BC，∵PQ∥OB，‎ ‎∴四边形BCPQ是平行四边形，‎ ‎∴PC∥AB，‎ ‎∵抛物线的解析式为y=x2+x②，‎ 令y=0，‎ ‎∴x2+x=0，‎ ‎∴x=0或x=﹣4，‎ ‎∴A（﹣4，0），‎ ‎∵B（4，8），‎ ‎∴直线AB解析式为y=x+4，设直线PC的解析式为y=x+m，‎ ‎∵C（2，4），‎ ‎∴直线PC的解析式为y=x+2②，‎ 联立①②解得，（舍）或，‎ ‎∴P（﹣2，﹣2+2）．‎ ‎　‎ ‎39．如图，在平面直角坐标系中，∠ACB=90°，OC=2OB，tan∠ABC=2，点B的坐标为（1，0）．抛物线y=﹣x2+bx+c经过A、B两点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE=DE．‎ ‎①求点P的坐标；‎ ‎②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．‎ ‎【解答】解：（1）∵B（1，0），‎ ‎∴OB=1，‎ ‎∵OC=2OB=2，‎ ‎∴C（﹣2，0），‎ Rt△ABC中，tan∠ABC=2，‎ ‎∴，‎ ‎∴，‎ ‎∴AC=6，‎ ‎∴A（﹣2，6），‎ 把A（﹣2，6）和B（1，0）代入y=﹣x2+bx+c得：，‎ 解得：，‎ ‎∴抛物线的解析式为：y=﹣x2﹣3x+4；‎ ‎（2）①∵A（﹣2，6），B（1，0），‎ 易得AB的解析式为：y=﹣2x+2，‎ 设P（x，﹣x2﹣3x+4），则E（x，﹣2x+2），‎ ‎∵PE=DE，‎ ‎∴﹣x2﹣3x+4﹣（﹣2x+2）=（﹣2x+2），‎ x=1（舍）或﹣1，‎ ‎∴P（﹣1，6）；‎ ‎②∵M在直线PD上，且P（﹣1，6），‎ 设M（﹣1，y），‎ ‎∴AM2=（﹣1+2）2+（y﹣6）2=1+（y﹣6）2，‎ BM2=（1+1）2+y2=4+y2，‎ AB2=（1+2）2+62=45，‎ 分三种情况：‎ i）当∠AMB=90°时，有AM2+BM2=AB2，‎ ‎∴1+（y﹣6）2+4+y2=45，‎ 解得：y=3，‎ ‎∴M（﹣1，3+）或（﹣1，3﹣）；‎ ii）当∠ABM=90°时，有AB2+BM2=AM2，‎ ‎∴45+4+y2=1+（y﹣6）2，‎ y=﹣1，‎ ‎∴M（﹣1，﹣1），‎ iii）当∠BAM=90°时，有AM2+AB2=BM2，‎ ‎∴1+（y﹣6）2+45=4+y2，‎ y=，‎ ‎∴M（﹣1，）；‎ 综上所述，点M的坐标为：∴M（﹣1，3+）或（﹣1，3﹣）或（﹣1，﹣1）或（﹣1，）．‎ ‎　‎ ‎40．如图1，经过原点O的抛物线y=ax2+bx（a、b为常数，a≠0）与x轴相交于另一点A（3，0）．直线l：y=x在第一象限内和此抛物线相交于点B（5，t），与抛物线的对称轴相交于点C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在x轴上找一点P，使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似，求满足条件的点P的坐标；‎ ‎（3）直线l沿着x轴向右平移得到直线l′，l′与线段OA相交于点M，与x轴下方的抛物线相交于点N，过点N作NE⊥x轴于点E．把△MEN沿直线l′折叠，当点E恰好落在抛物线上时（图2），求直线l′的解析式；‎ ‎（4）在（3）问的条件下（图3），直线l′与y轴相交于点K，把△MOK绕点O顺时针旋转90°得到△M′OK′，点F为直线l′上的动点．当△M'FK′为等腰三角形时，求满足条件的点F的坐标．‎ ‎【解答】解：（1）由已知点B坐标为（5，5）‎ 把点B（5，5），A（3，0）代入y=ax2+bx，得 解得 ‎∴抛物线的解析式为：y=‎ ‎（2）由（1）抛物线对称轴为直线x=，则点C坐标为（，）‎ ‎∴OC=，OB=5‎ 当△OBA∽△OCP时，‎ ‎∴‎ ‎∴OP=‎ 当△OBA∽△OPC时，‎ ‎∴‎ ‎∴OP=5‎ ‎∴点P坐标为（5，0）或（，0）‎ ‎（3）设点N坐标为（a，b），直线l′解析式为：y=x+c ‎∵直线l′y=x+c与x轴夹角为45°‎ ‎∴△MEN为等腰直角三角形．‎ 当把△MEN沿直线l′折叠时，四边形ENE′M为正方形 ‎∴点E′坐标为（a﹣b，b）‎ ‎∵EE′平行于x轴 ‎∴E、E′关于抛物线对称轴对称 ‎∵‎ ‎∴b=2a﹣3‎ 则点N坐标可化为（a，2a﹣3）‎ 把点N坐标带入y=‎ 得：‎ ‎2a﹣3=‎ 解得 a1=1，a2=6‎ ‎∵a=6时，b=2a﹣3=﹣9‎ 由函数解析式可知函数最小值为﹣‎ ‎∴﹣＜6‎ ‎∴a=6舍去 则点N坐标为（1，﹣1）‎ 把N坐标代入y=x+c 则c=﹣2‎ ‎∴直线l′的解析式为：y=x﹣2‎ ‎（4）由（3）K点坐标为（0，﹣2）‎ 则△MOK为等腰直角三角形 ‎∴△M′OK′为等腰直角三角形，M′K′⊥直线l′‎ ‎∴当M′K′=M′F时，△M'FK′为等腰直角三角形 ‎∴F坐标为（2，0）或（﹣2，﹣4）‎ ‎　‎