中考浙江圆带答案

中考浙江圆带答案

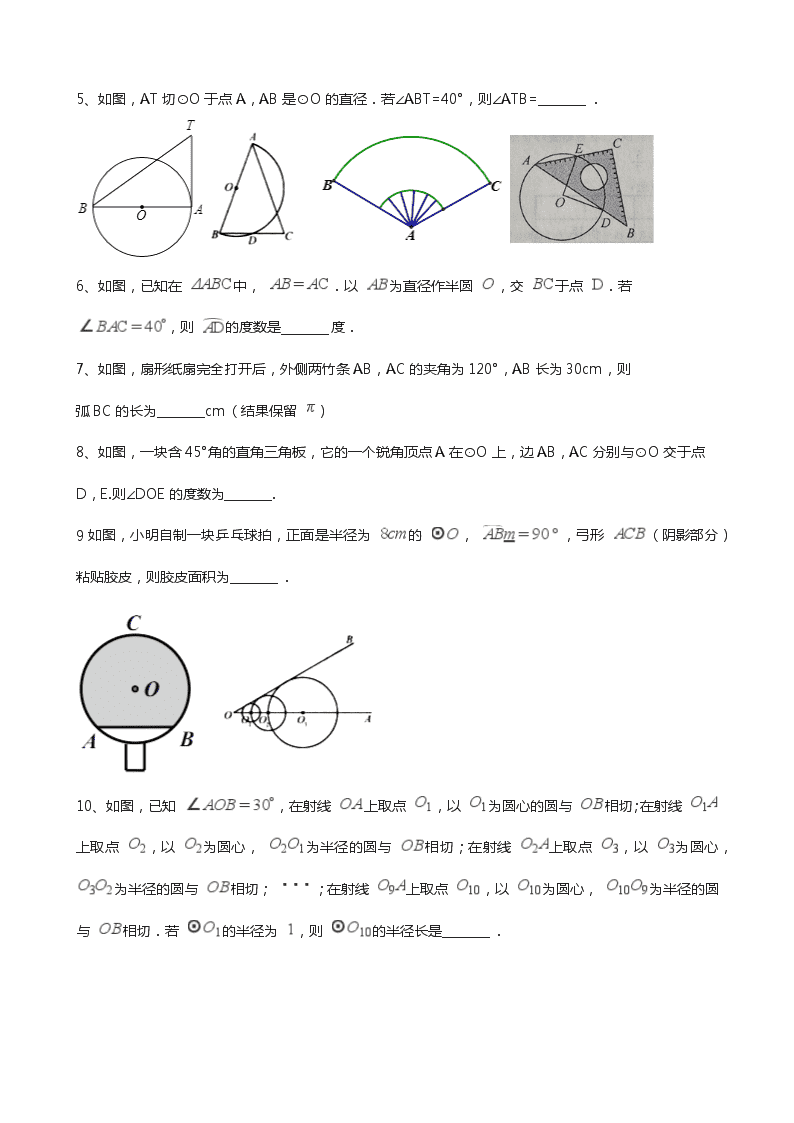
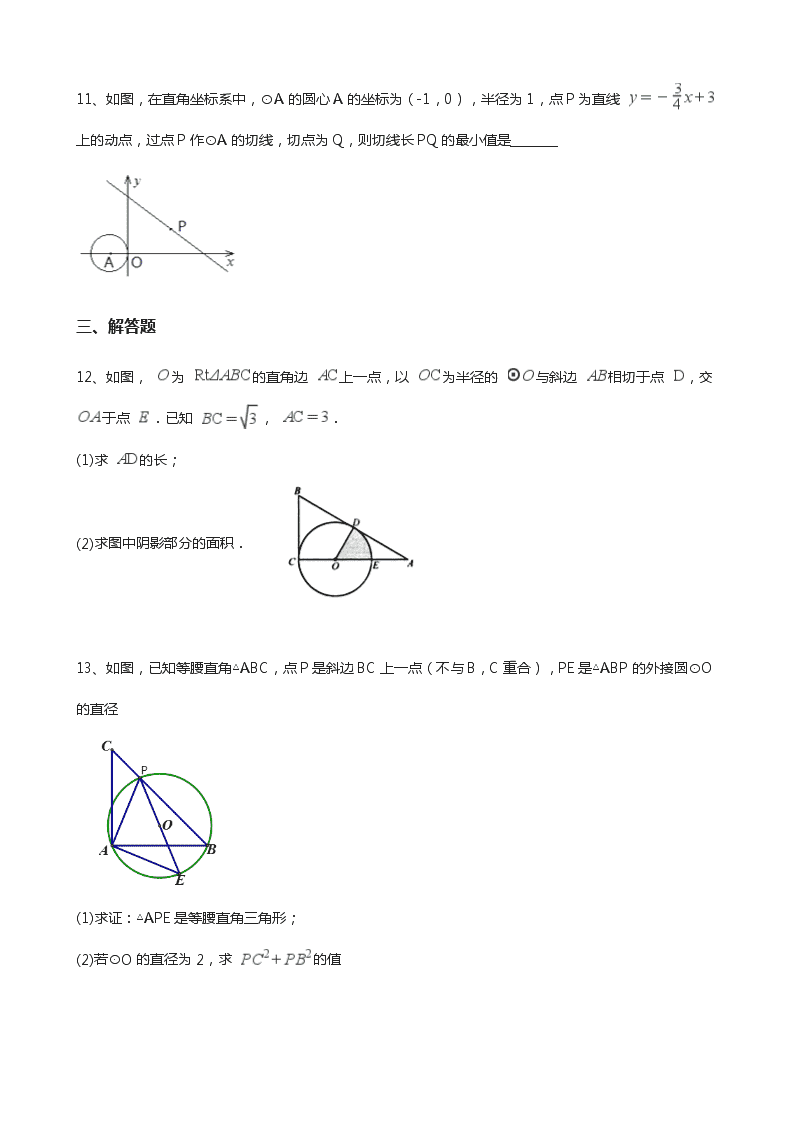
‎2017年专题11 圆 一、单选题 ‎1、如图，在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片，则弓形弦AB的长为（      ) ‎ A、10cmB、16cmC、24cmD、26cm ‎2、如图，在Rt△ABC中，∠A＝90°，BC＝ ．以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点，则 的长为           （        ） A、B、C、D、‎ ‎3、如图，点C是以AB为直径的半圆O的三等分点，AC=2，则图中阴影部分的面积是（    ） A、B、C、D、‎ ‎4、运用图形变化的方法研究下列问题：如图，AB是⊙O的直径，CD，EF是⊙O的弦，且AB∥CD∥EF，AB=10，CD=6，EF=8。则图中阴影部分的面积是（       ） ‎ A、B、C、D、‎ 二、填空题 ‎5、如图，AT切⊙O于点A，AB是⊙O的直径．若∠ABT=40°，则∠ATB=________． ‎ ‎6、如图，已知在 中， ．以 为直径作半圆 ，交 于点 ．若 ，则 的度数是________度． 7、如图，扇形纸扇完全打开后，外侧两竹条AB，AC的夹角为120°，AB长为30cm，则 弧BC的长为________cm（结果保留 ） 8、如图，一块含45°角的直角三角板，它的一个锐角顶点A在⊙O上，边AB，AC分别与⊙O交于点D，E.则∠DOE的度数为________. 9如图，小明自制一块乒乓球拍，正面是半径为 的 ， ，弓形 （阴影部分）粘贴胶皮，则胶皮面积为________． ‎ ‎10、如图，已知 ，在射线 上取点 ，以 为圆心的圆与 相切；在射线 上取点 ，以 为圆心， 为半径的圆与 相切；在射线 上取点 ，以 为圆心， 为半径的圆与 相切； ；在射线 上取点 ，以 为圆心， 为半径的圆与 相切．若 的半径为 ，则 的半径长是________． ‎ ‎11、如图，在直角坐标系中，⊙A的圆心A的坐标为（-1，0），半径为1，点P为直线 上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是________ ‎ 三、解答题 ‎12、如图， 为 的直角边 上一点，以 为半径的 与斜边 相切于点 ，交 于点 ．已知 ， ． (1)求 的长； ‎ ‎(2)求图中阴影部分的面积． ‎ ‎13、如图，已知等腰直角△ABC，点P是斜边BC上一点（不与B，C重合），PE是△ABP的外接圆⊙O的直径 ‎ ‎(1)求证：△APE是等腰直角三角形； ‎ ‎(2)若⊙O的直径为2，求 的值 ‎ ‎14、如图，AB为半圆O的直径，C为BA延长线上一点，CD切半圆O于点D。连结OD，作BE⊥CD于点E，交半圆O于点F。已知CE=12，BE=9 ‎ ‎(1)求证：△COD∽△CBE； ‎ ‎(2)求半圆O的半径 的长 ‎ ‎15、如图，在Rt△ABC中，∠C=Rt∠，以BC为直径的⊙O交AB于点D，切线DE交AC于点E. ‎ ‎(1)求证：∠A=∠ADE； ‎ ‎(2)若AD=16，DE=10，求BC的长. ‎ ‎16、如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE． ‎ ‎(1)当∠APB=28°时，求∠B和 的度数； ‎ ‎(2)求证：AC=AB． ‎ ‎(3)在点P的运动过程中 ①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值； ②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比． ‎ ‎17、如图，在△ABC中，AC=BC，∠ACB=90°，⊙O（圆心O在△ABC内部）经过B、C两点，交AB于点E，过点E作⊙O的切线交AC于点F．延长CO交AB于点G，作ED∥AC交CG于点D ‎ ‎(1)求证：四边形CDEF是平行四边形； ‎ ‎(2)若BC=3，tan∠DEF=2，求BG的值． ‎ ‎18如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ， ‎ ‎(1)点点同学通过画图和测量得到以下近似数据：‎ ɑ ‎30°‎ ‎40°‎ ‎50°‎ ‎60°‎ β ‎120°‎ ‎130°‎ ‎140°‎ ‎150°‎ γ ‎150°‎ ‎140°‎ ‎130°‎ ‎120°‎ 猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明： ‎ ‎(2)若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长． ‎ ‎19、两个内角分别是它们对角的一半的四边形叫做半对角四边形． ‎ ‎(1)如图1，在半对角四边形ABCD中，∠B＝ ∠D，∠C＝ ∠A，求∠B与∠C的度数之和； ‎ ‎(2)如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF． 求证：四边形DBCF是半对角四边形； ‎ ‎(3)如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当DH＝BG时，求△BGH与△ABC的面积之比． ‎ ‎20、 如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D.E是AB延长线上一点，CE交⊙O于点F,连结OC,AC. ‎ ‎(1)求证:AC平分∠DAO. ‎ ‎(2)若∠DAO=105°，∠E=30°. ①求∠OCE的度数. ②若⊙O的半径为2 ，求线段EF的长. ‎