中考图形变换练习题

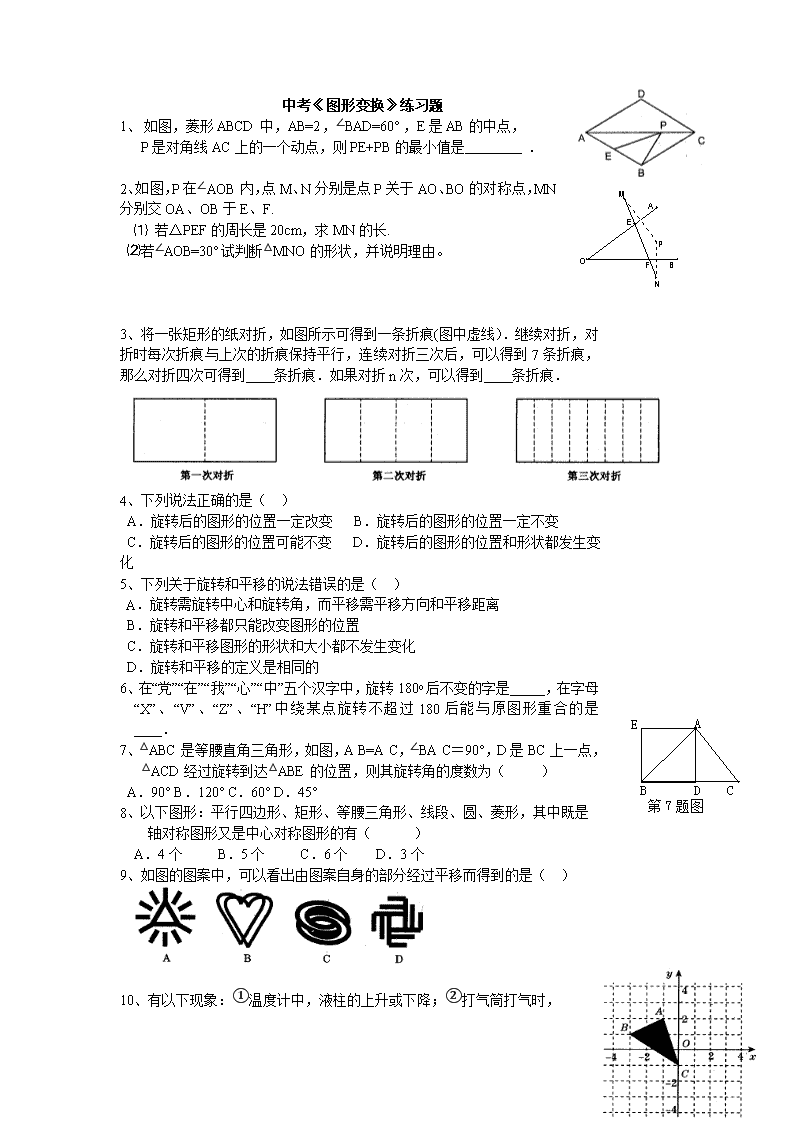
中考图形变换练习题

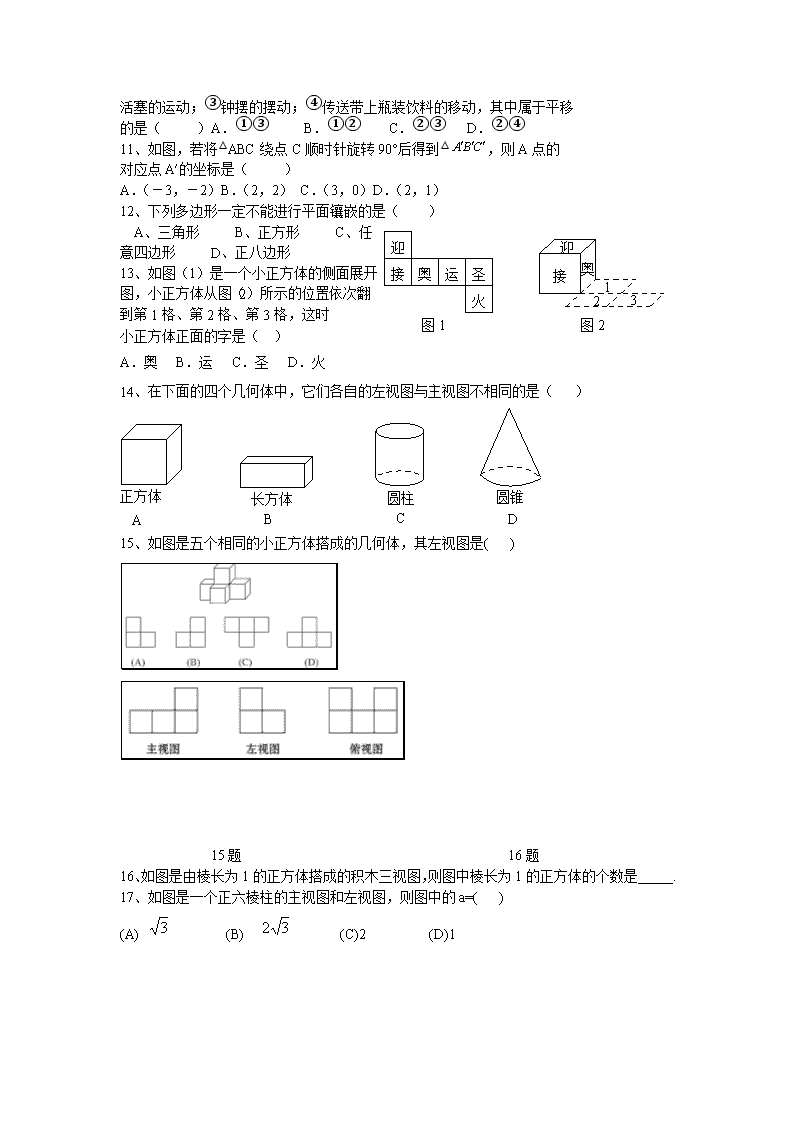
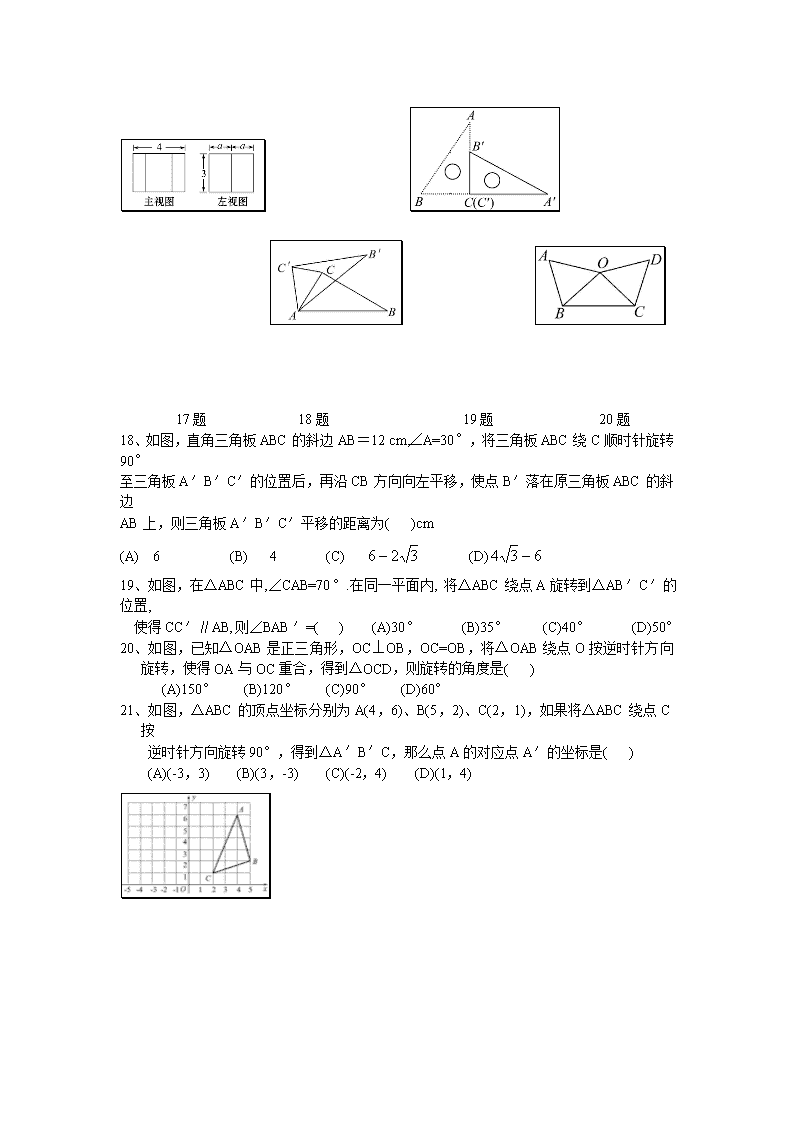
中考《图形变换》练习题 1、 如图，菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，‎ P是对角线AC上的一个动点，则PE+PB的最小值是　　　 ．‎ ‎2、如图，P在∠AOB内，点M、N分别是点P关于AO、BO的对称点，MN分别交OA、OB于E、F. ‎ ‎⑴ 若△PEF的周长是20cm，求MN的长.‎ ‎ ⑵若∠AOB=30°试判断△MNO的形状，并说明理由。‎ ‎3、将一张矩形的纸对折，如图所示可得到一条折痕(图中虚线）．继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折四次可得到 条折痕．如果对折n次，可以得到 条折痕．‎ ‎4、下列说法正确的是（ ）‎ A．旋转后的图形的位置一定改变 B．旋转后的图形的位置一定不变 C．旋转后的图形的位置可能不变 D．旋转后的图形的位置和形状都发生变化 ‎5、下列关于旋转和平移的说法错误的是（ ）‎ A．旋转需旋转中心和旋转角，而平移需平移方向和平移距离 B．旋转和平移都只能改变图形的位置 C．旋转和平移图形的形状和大小都不发生变化 D．旋转和平移的定义是相同的 第7题图 A B C D E ‎6、在“党”“在”“我”“心”“中”五个汉字中，旋转180o后不变的字是_____，在字母“X”、“V”、“Z”、“H”中绕某点旋转不超过180后能与原图形重合的是____．‎ ‎7、△ABC是等腰直角三角形，如图，A B=A C，∠BA C＝90°，D是BC上一点，‎ ‎△ACD经过旋转到达△ABE的位置，则其旋转角的度数为（ ）‎ A．90° B．120° C．60° D．45°‎ ‎8、以下图形：平行四边形、矩形、等腰三角形、线段、圆、菱形，其中既是 轴对称图形又是中心对称图形的有（ ）‎ ‎ A．4个 B．5个 C．6个 D．3个 ‎9、如图的图案中，可以看出由图案自身的部分经过平移而得到的是（ ） ‎ ‎ ‎ ‎10、有以下现象：①温度计中，液柱的上升或下降；②打气筒打气时，‎ 活塞的运动；③钟摆的摆动；④传送带上瓶装饮料的移动，其中属于平移 的是（ ）A．①③ B．①② C．②③ D．②④‎ ‎11、如图，若将△ABC绕点C顺时针旋转90°后得到△，则A点的 对应点A′的坐标是（ ） ‎ A．（－3，－2）B．（2，2） C．（3，0）D．（2，1）‎ ‎12、下列多边形一定不能进行平面镶嵌的是（ ）‎ A、三角形 B、正方形 C、任意四边形 D、正八边形 迎 接 奥 运 圣 火 图1‎ 迎 接 奥 ‎1‎ ‎2‎ ‎3‎ 图2‎ ‎13、如图（1）是一个小正方体的侧面展开图，小正方体从图（2）所示的位置依次翻到第1格、第2格、第3格，这时 小正方体正面的字是（ ）‎ A．奥 B．运 C．圣 D．火 ‎14、在下面的四个几何体中，它们各自的左视图与主视图不相同的是（ ）‎ 正方体 长方体 圆柱 圆锥 A B C D ‎15、如图是五个相同的小正方体搭成的几何体，其左视图是( )‎ ‎ ‎ ‎ 15题 16题 ‎16、如图是由棱长为1的正方体搭成的积木三视图，则图中棱长为1的正方体的个数是_____.‎ ‎17、如图是一个正六棱柱的主视图和左视图，则图中的a=( )‎ ‎(A) (B) (C)2 (D)1‎ ‎ 17题 18题 19题 20题 ‎18、如图，直角三角板ABC的斜边AB＝12 cm,∠A=30°，将三角板ABC绕C顺时针旋转90°‎ 至三角板A′B′C′的位置后，再沿CB方向向左平移，使点B′落在原三角板ABC的斜边 AB上，则三角板A′B′C′平移的距离为( )cm ‎(A) 6 (B) 4 (C) (D)‎ ‎19、如图，在△ABC中,∠CAB=70°.在同一平面内, 将△ABC绕点A旋转到△AB′C′的位置, ‎ 使得CC′∥AB,则∠BAB′=( ) (A)30° (B)35° (C)40° (D)50°‎ ‎20、如图，已知△OAB是正三角形，OC⊥OB，OC=OB，将△OAB绕点O按逆时针方向旋转，使得OA与OC重合，得到△OCD，则旋转的角度是( )‎ ‎(A)150° (B)120° (C)90° (D)60°‎ ‎21、如图，△ABC的顶点坐标分别为A(4，6)、B(5，2)、C(2，1)，如果将△ABC绕点C按 逆时针方向旋转90°，得到△A′B′C，那么点A的对应点A′的坐标是( )‎ ‎(A)(-3，3) (B)(3，-3) (C)(-2，4) (D)(1，4)‎ ‎ ‎ ‎ ‎ ‎ 21题 22题 23题 ‎22、如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是_____.‎ ‎23、如图，已知正方形ABCD的边长为12 cm,E为CD边上一点，DE＝5 cm.以点A为中心，将△ADE按顺时针方向旋转得△ABF，则点E所经过的路径长为_____cm.‎ ‎24、在△ABC中，AB=BC=2，∠ABC=120°,将△ABC绕点B顺时针旋转角α(0<α<120°),得A1BC1，交AC于点E，A1C1分别交AC、BC于D、F两点.‎ ‎(1)如图①，观察并猜想，在旋转过程中，线段EA1与FC有怎样的数量关系？并证明你的结论.‎ ‎2)如图②，当α=30°时，试判断四边形BC1DA的形状，并说明理由.‎ ‎(3)在(2)的情况下，求ED的长.‎ ‎25、将两块全等的含30°角的三角尺如图(1)摆放在一起,它们的较短直角边长为3.‎ ‎(1)将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=_____;‎ ‎(2)将△ECD绕点C逆时针旋转到图(3)的位置,使点E落在AB上,则△ECD绕点C旋转的度数=_____;‎ ‎(3)将△ECD沿直线AC翻折到图(4)的位置,ED′与AB相交于点F,求证:AF=FD′.‎