2015南京市玄武区中考数学一模试卷与答案

2015南京市玄武区中考数学一模试卷与答案

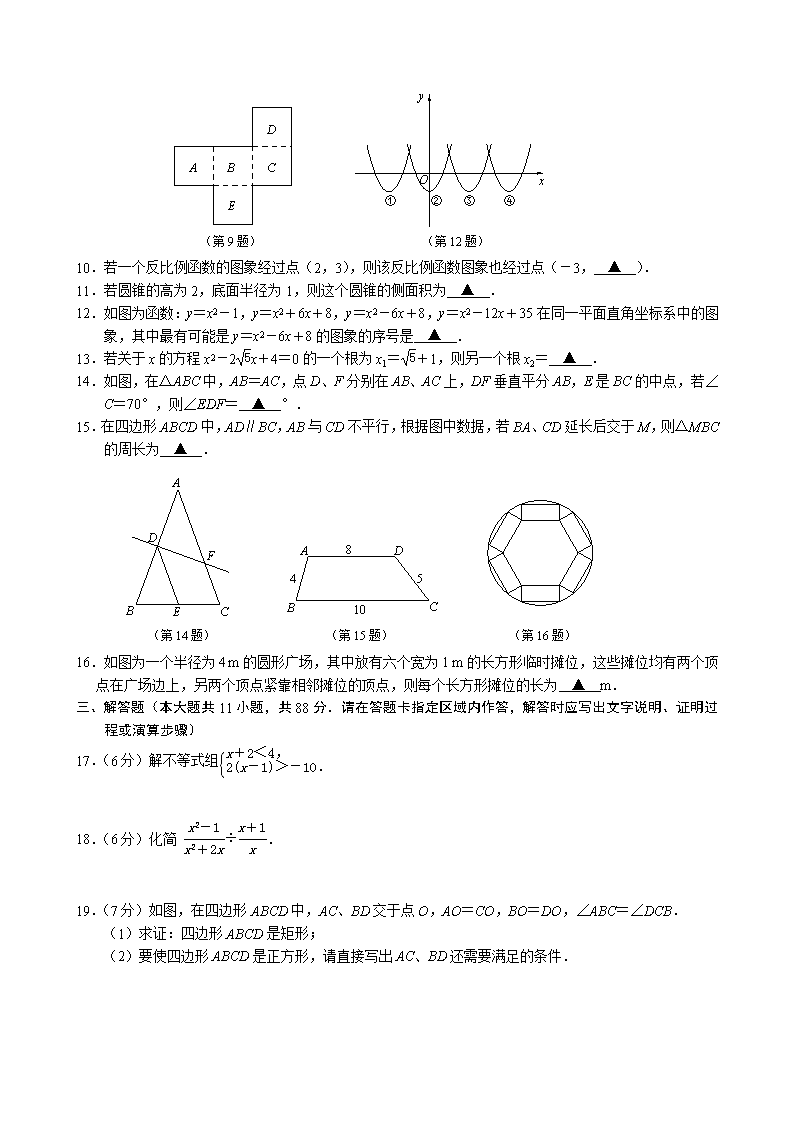
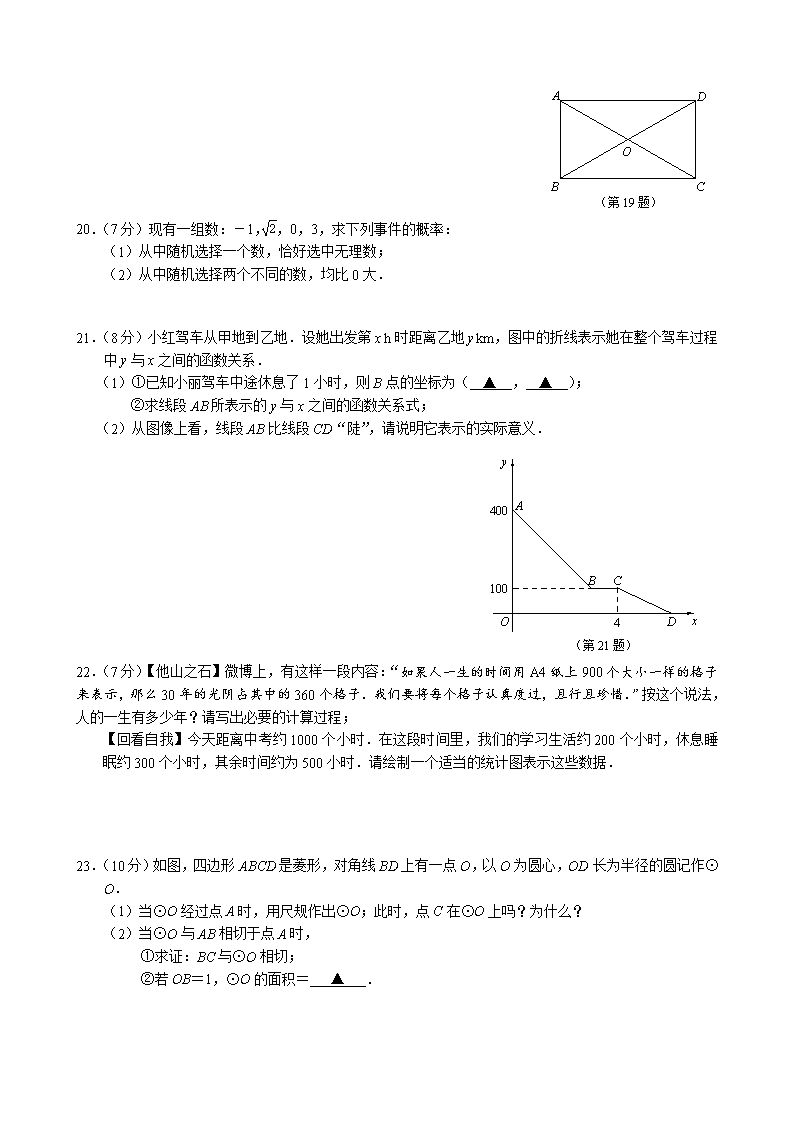
‎2014~2015学年第二学期九年级测试卷 玄武区一模 数 学 一、选择题（本大题共6小题，每小题2分，共12分）‎ ‎1．等于 A．－ B． C． －2‎ D．2‎ ‎2．9的平方根等于 A．－3‎ B．3‎ C．±3‎ D． ‎3．2014年，南京中考考生约46000人，则数据46000用科学记数法表示为 A．0.46×105‎ B．4.6×103‎ C．4.6×104‎ D．4.6×105‎ ‎4．计算a2÷a3的结果是 A．a－1‎ B．a C．a5‎ D．a6‎ ‎5．我们常用“y随x的增大而增大（或减小）”来表示两个变量之间的变化关系．有这样一个情境：如图，小王从点A经过路灯C的正下方沿直线走到点B，他与路灯C的距离y随他与点A之间的距离x的变化而变化．下列函数中y与x之间的变化关系，最有可能与上述情境类似的是 A．y＝x B．y＝x＋3‎ C．y＝ D．y＝(x－3)2＋3‎ C A B ‎（第5题）‎ ‎ O A B C D E ‎（第6题）‎ ‎ ‎6．如图，半径为1的⊙O与正五边形ABCDE相切于点A、C，则劣弧的长度为 ‎ A．π ‎ B．π ‎ C．π ‎ D．π 二、填空题（本大题共10小题，每小题2分，共20分．）‎ ‎7．使式子有意义的x的取值范围是 ▲ ．‎ ‎8．若李老师六个月的手机上网流量（单位：M）分别为526，600，874，480，620，500，则李老师这六个月平均每个月的手机上网流量为 ▲ M．‎ ‎9．如果按图中虚线对折可以做成一个上底面为无盖的盒子，那么该盒子的下底面的字母是 ▲ ．‎ A B C D E ‎（第9题）‎ ‎ ‎y x O ‎①‎ ‎②‎ ‎④‎ ‎③‎ ‎（第12题）‎ ‎10．若一个反比例函数的图象经过点（2，3），则该反比例函数图象也经过点（－3， ▲ ）．‎ ‎11．若圆锥的高为2，底面半径为1，则这个圆锥的侧面积为 ▲ ．‎ ‎12．如图为函数：y＝x2－1，y＝x2＋6x＋8，y＝x2－6x＋8，y＝x2－12x＋35在同一平面直角坐标系中的图象，其中最有可能是y＝x2－6x＋8的图象的序号是 ▲ ．‎ ‎13．若关于x的方程x2－2x＋4＝0的一个根为x1＝＋1，则另一个根x2＝ ▲ ．‎ ‎14．如图，在△ABC中，AB＝AC，点D、F分别在AB、AC上，DF垂直平分AB，E是BC的中点，若∠C＝70°，则∠EDF＝ ▲ °．‎ ‎15．在四边形ABCD中，AD∥BC，AB与CD不平行，根据图中数据，若BA、CD延长后交于M，则△MBC的周长为 ▲ ．‎ A B C D E F ‎（第14题）‎ ‎ A B C D ‎8‎ ‎10‎ ‎4‎ ‎5‎ ‎（第15题）‎ ‎‎（第16题）‎ ‎16．如图为一个半径为4 m的圆形广场，其中放有六个宽为1 m的长方形临时摊位，这些摊位均有两个顶点在广场边上，另两个顶点紧靠相邻摊位的顶点，则每个长方形摊位的长为 ▲ m．‎ 三、解答题（本大题共11小题，共88分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．（6分）解不等式组 ‎ ‎18．（6分）化简 ÷． ‎ ‎19．（7分）如图，在四边形ABCD中，AC、BD交于点O，AO＝CO，BO＝DO，∠ABC＝∠DCB．‎ ‎（1）求证：四边形ABCD是矩形；‎ ‎（2）要使四边形ABCD是正方形，请直接写出AC、BD还需要满足的条件．‎ A B C D O ‎（第19题）‎ ‎20．（7分）现有一组数：－1，，0，3，求下列事件的概率：‎ ‎（1）从中随机选择一个数，恰好选中无理数；‎ ‎（2）从中随机选择两个不同的数，均比0大． ‎ ‎21．（8分）小红驾车从甲地到乙地．设她出发第x h时距离乙地y km，图中的折线表示她在整个驾车过程中y与x之间的函数关系．‎ ‎（1）①已知小丽驾车中途休息了1小时，则B点的坐标为（ ▲ ， ▲ ）；‎ ‎②求线段AB所表示的y与x之间的函数关系式；‎ ‎（2）从图像上看，线段AB比线段CD“陡”，请说明它表示的实际意义．‎ y x O D C B A ‎400‎ ‎100‎ ‎4‎ ‎（第21题）‎ ‎22．（7分）【他山之石】微博上，有这样一段内容：“如果人一生的时间用A4纸上900个大小一样的格子来表示，那么30年的光阴占其中的360个格子．我们要将每个格子认真度过，且行且珍惜．”按这个说法，人的一生有多少年？请写出必要的计算过程；‎ ‎【回看自我】今天距离中考约1000个小时．在这段时间里，我们的学习生活约200个小时，休息睡眠约300个小时，其余时间约为500小时．请绘制一个适当的统计图表示这些数据．‎ ‎23．（10分）如图，四边形ABCD是菱形，对角线BD上有一点O，以O为圆心，OD长为半径的圆记作⊙O．‎ ‎（1）当⊙O经过点A时，用尺规作出⊙O；此时，点C在⊙O上吗？为什么？‎ ‎（2）当⊙O与AB相切于点A时，‎ ‎①求证：BC与⊙O相切；‎ ‎②若OB＝1，⊙O的面积＝ ▲ ．‎ C B A D ‎（第23题）‎ ‎24．（8分）在某两个时刻，太阳光线与地面的夹角分别为37°和45°，树AB长6 m．‎ ‎（1）如图①，若树与地面l的夹角为90°，则两次影长的和CD＝ ▲ m；‎ ‎（2）如图②，若树与地面l的夹角为α，求两次影长的和CD（用含α的式子表示）．‎ ‎（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．）‎ ‎（第24题）‎ ‎①‎ A D ‎37°‎ C B ‎45°‎ A D ‎37°‎ C B ‎45°‎ α ‎②‎ l l ‎25．（8分）已知A市出租车原收费标准如下：不超过3 km的路程按起步价10元收费，超过3 km以外的路程按2.4元/km收费．为了减少出租车空车返回的损失，现A市决定实施返空费方案，设出租车行驶的路程为x km，具体方案如下：当0＜x≤20时，按原收费标准收费；当x＞20时，在原收费标准基础上，再加收0.01x元/km．例如，当出租车行驶了50 km时，收费总额为：2.4×(50－3)＋10＋(0.01×50)×(50－20)＝137.8（元）．‎ ‎（1）A市实施返空费方案后，当x＞20时，求收费总额y（元）与x（km）的函数关系式；‎ ‎（2）自4月1日起，南京市实施的返空费方案是：不超过20 km的路程，与A市的原收费标准相同；超过20 km以外的路程，按原单价2.4元/km的1.5倍收费．若行驶路程x超过20 km，分别按两市返空费方案计算，当收费总额相同时，求x的值．‎ ‎26．（10分）已知二次函数y＝a(x－m)2－a(x－m)（a、m为常数，且a≠0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，其顶点为D．‎ ‎（1）求点A、B的坐标；‎ ‎（2）过点D作x轴的垂线，垂足为E．若△CBO与△DAE相似（O为坐标原点），试讨论m与a的关系；‎ ‎（3）在同一平面直角坐标系中，若该二次函数的图象与二次函数y＝－a(x－m)2＋a(x－m)的图象组合成一个新的图形，则这个新图形的对称轴为 ▲ ．‎ ‎27．（11分）（1）如图①，在△ABC中，AB＝AC，O为BC中点．直线l从与边BC重合开始绕点O顺时针旋转，在旋转过程中，直线l与AB边交于点P，与AC的延长线交于点Q．△APQ面积的变化情况是 ▲ （填“变大”、“变小”、“先变大再变小”或“先变小再变大”），请说明理由．‎ ‎（第27题）‎ O Q P ‎①‎ l A B C l P B C ‎②‎ A Q O l ‎ ‎ ‎（2）如图②，O为△ABC的内心，直线l经过点O，与AB、AC分别交于点P、Q，AP＝AQ．图中阴影部分为直线l截△ABC所形成．将直线l绕点O顺时针旋转180°，请画图并说明：随着直线l位置的变化，阴影部分的面积是如何变化的？‎ ‎（注：图③给出了直线l截△ABC所形成阴影部分的某些情形）‎ ‎③‎ ‎2014~2015学年第二学期九年级测试卷 数学试题参考答案及评分标准 说明：本评分标准每题给出了一种或几种解法供参考，如果考生的解法与本解答不同，参照本评分标准的精神给分．‎ 一、选择题（本大题共6小题，每小题2分，共12分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 答案 D C C A D B 二、填空题（本大题共10小题，每小题2分，共20分）‎ ‎7．x≠1； 8．600 9．B 10．－2 11．π ‎ ‎12．③ 13．－1 14．50 15．55 16． 三、解答题（本大题共11小题，共88分）‎ ‎17．（本题6分）‎ 解： 解不等式①，得 x＜2． ‎ 解不等式②，得x＞－4． ‎ 所以，不等式组的解集是－4＜x＜2． 6分 ‎18．（本题6分）‎ 解：÷ ‎ ‎＝· ‎＝· ‎ ‎＝． 6分 ‎ ‎19．（本题7分）‎ ‎（1）证明：∵AO＝CO，BO＝DO，‎ ‎∴四边形ABCD是平行四边形．‎ ‎∴AB∥CD，‎ ‎∴∠ABC＋∠DCB＝180°．‎ ‎∵∠ABC＝∠DCB，‎ ‎∴∠ABC＝∠DCB＝90°．‎ ‎∴□ABCD是矩形． 5分 ‎（2）AC⊥BD． 7分 ‎20．（本题7分）‎ 解：（1）无理数为，从中随机选择一个数，恰好选中无理数的概率为． 2分 ‎（2）从中随机选择两个不同的数，所有可能出现的结果有：‎ ‎（－1，）、（－1，0）、（－1，3）、（，0）、（，3）、（0，3），‎ 共有6种，它们出现的可能性相同．所有的结果中，满足“均比0大”（记为事件A）的结果有1种，所以P(A)＝． 7分 ‎ ‎21．（本题8分）‎ 解：（1）①（ 3 ， 100 ）； 2分 ‎②设y与x之间的函数关系式为y＝kx＋b．‎ 根据题意，当x＝0时，y＝400；当x＝3时，y＝100．‎ 所以解得 所以，y与x之间的函数关系式为y＝－100x＋400． 6分 ‎（2）AB段驾车速度比CD段驾车速度快． 8分 ‎22．（本题7分）‎ ‎【他山之石】解：30÷＝75‎ 答：按这个说法，人的一生有75年． 2分 ‎【回看自我】‎ 时间/小时 在校 ‎100‎ ‎200‎ ‎300‎ ‎400‎ ‎0‎ ‎200‎ ‎300‎ ‎500‎ 休息 其余 项目 距离中考时间条形统计图 ‎①‎ 其余 ‎40%‎ 休息 ‎30%‎ 在校 ‎20%‎ 距离中考时间扇形统计图 ‎②‎ ‎500‎ ‎ 7分 C B A D O ‎23．（本题10分）‎ ‎（1）解：如图，⊙O为所求． 2分 点C在⊙O上，理由如下：‎ 连接OC，‎ 在菱形ABCD中，AD＝CD，∠ADO＝∠CDO，‎ 又∵DO＝DO，‎ ‎∴△ADO≌△CDO．‎ ‎∴AO＝CO．‎ ‎∴点C在⊙O上． 5分 ‎（2）①证明：∵⊙O与AB相切于点A，∴∠OAB＝90°．‎ 由（1）可知，点C在⊙O上，∴AO＝CO．‎ 在菱形ABCD中，AB＝CB，‎ 又∵BO＝BO，∴△OAB≌△OCB，∴∠OCB＝∠OAB＝90°，即OC⊥BC．‎ 又∵点C在⊙O上，∴BC与⊙O相切． 8分 ‎ ②π． 10分 ‎24．（本题8分）‎ 解：（1）14； 2分 ‎（2）如图，作AH⊥CD，垂足为H．‎ A D ‎37°‎ C B ‎45°‎ α°‎ l H 在Rt△ABH中，sinα＝，即AH＝sinα·AB＝6sinα．‎ 在Rt△ADH中，tan45°＝，即HD＝＝6sinα．‎ 在Rt△ACH中，tan37°＝，即HC＝＝8sinα．‎ 两次影长的和CD＝HC＋HD＝14sinα (m)． 8分 ‎25．（本题8分）‎ 解：（1）y＝2.4(x－3)＋10＋0.01x(x－20)＝0.01x2＋2.2x＋2.8． 4分 ‎（2）解法1：当x＞20时，南京市y与x的函数关系式为：‎ y＝2.4(x－3)＋10＋2.4(1＋50%)(x－20)＝6x－69.2．‎ 根据题意，得6x－69.2＝0.01x2＋2.2x＋2.8．‎ 解得 x1＝20（舍去），x2＝360．‎ 答：当x＞20且两市计费总额相同时，x＝360． 8分 解法2：已知当x≤20时，两市的计费方法相同，‎ 则当x＞20且两市计费总额相同时，‎ 即0.01x＝2.4(1＋50%)，‎ 解得x＝360．‎ 答：当x＞20且两市计费总额相同时，x＝360． 8分 ‎26．（本题10分）‎ 解：（1）当y＝0时，a(x－m)2－a(x－m)＝0．解得x1＝m，x2＝m＋1．‎ ‎∵点A在点B的左侧，∴A（m，0），B（m＋1，0）． 4分 ‎（2）当x＝0时，y＝am2＋am．可得C（0，am2＋am）．‎ y＝a(x－m)2－a(x－m)＝a(x－)2－，‎ ‎∴点D的坐标为（，－）．‎ ‎∵△CBO与△DAE相似且∠COB＝∠DEA＝90°，‎ ‎∴＝或＝，即＝或＝，‎ 解得 a2m＝±2，且a≠0，m≠－1；‎ 或者，当m＝±时，a可取一切非零实数． 8分 ‎（3）x轴所在直线，直线x＝． 10分 ‎27．（本题11分）‎ 解：（1）变大，理由如下：‎ 如图，作CM∥PB，交直线l于点M．‎ ‎∵CM∥PB，∴∠PBO＝∠MCO．‎ ‎∵O是BC中点，∴BO＝CO．‎ 又∵∠POB＝∠MOC，∴△POB≌△MOC．‎ 易得，△COQ的面积大于△BOP的面积．‎ 则在直线l从与BC重合开始，绕BC中点O顺时针旋转的过程中，‎ ‎△APQ面积的变化情况是变大． 4分 O Q P l A B C l M ‎ ‎B C A O D E F P Q P1‎ Q1‎ P2‎ Q2‎ ‎（2）如图，连接AO、BO、CO并延长，分别交BC、AC、AB于点D、E、F．‎ 作PQ⊥AD，P1Q1⊥BE，P2Q2⊥CF，垂足均为O．‎ 易得，所作点P、Q即为原题中P、Q．‎ 当直线l从直线PQ的位置绕点O顺时针旋转至直线P1Q1的位置的过程中，‎ 阴影部分面积逐渐变大；‎ 当直线l从直线P1Q1的位置绕点O顺时针旋转至直线P2Q2的位置的过程中，‎ 阴影部分面积逐渐变小；‎ 当直线l从直线P2Q2的位置绕点O顺时针旋转至直线PQ的位置的过程中，‎ 阴影部分面积逐渐变大． 11分