江苏专用2018_2019学年高中数学圆锥曲线与方程2.4抛物线2.4.2抛物线的几何性质学案苏教版

江苏专用2018_2019学年高中数学圆锥曲线与方程2.4抛物线2.4.2抛物线的几何性质学案苏教版

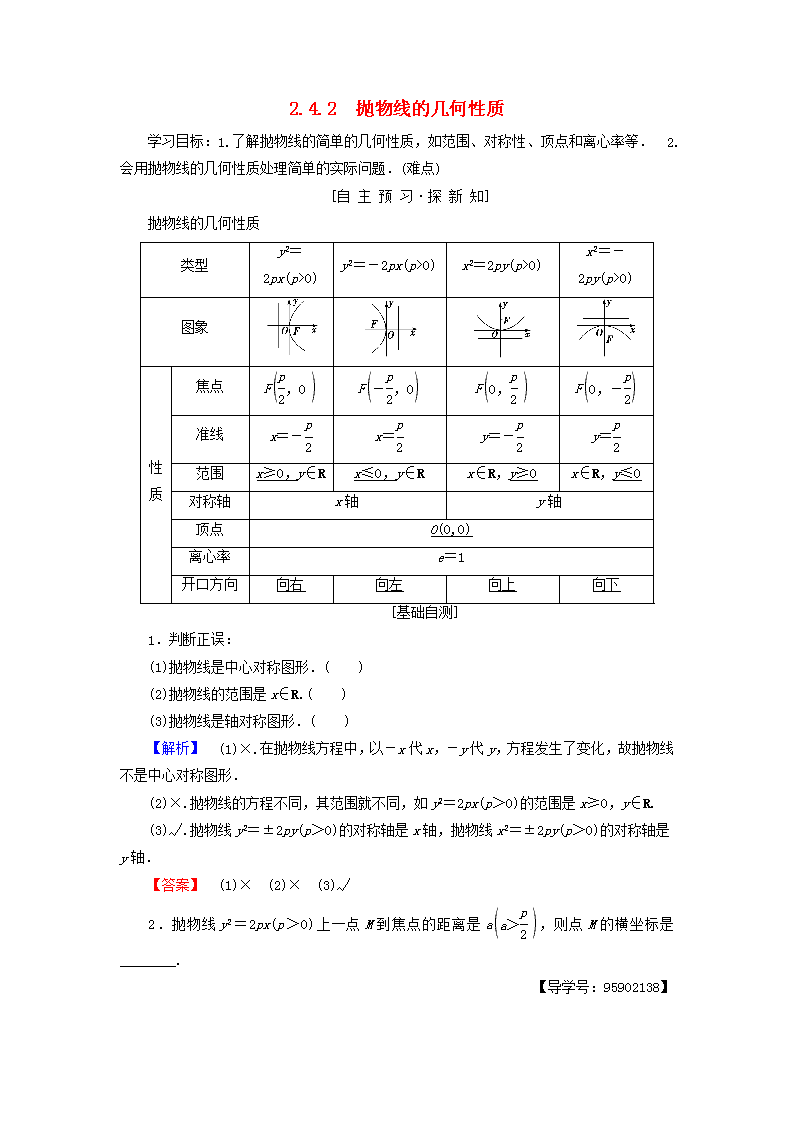
2.4.2　抛物线的几何性质学习目标：1.了解抛物线的简单的几何性质，如范围、对称性、顶点和离心率等．　2.会用抛物线的几何性质处理简单的实际问题．(难点)[自主预习·探新知]抛物线的几何性质类型y2＝2px(p>0)y2＝－2px(p>0)x2＝2py(p>0)x2＝－2py(p>0)图象性质焦点FFFF准线x＝－x＝y＝－y＝范围x≥0，y∈Rx≤0，y∈Rx∈R，y≥0x∈R，y≤0对称轴x轴y轴顶点O(0,0)离心率e＝1开口方向向右向左向上向下[基础自测]1．判断正误：(1)抛物线是中心对称图形．(　　)(2)抛物线的范围是x∈R.(　　)(3)抛物线是轴对称图形．(　　)【解析】　(1)×.在抛物线方程中，以－x代x，－y代y，方程发生了变化，故抛物线不是中心对称图形．(2)×.抛物线的方程不同，其范围就不同，如y2＝2px(p＞0)的范围是x≥0，y∈R.(3)√.抛物线y2＝±2py(p＞0)的对称轴是x轴，抛物线x2＝±2py(p＞0)的对称轴是y轴．【答案】　(1)×　(2)×　(3)√2．抛物线y2＝2px(p＞0)上一点M到焦点的距离是a，则点M的横坐标是________.【导学号：95902138】n【解析】　由抛物线的定义知：点M到焦点的距离a等于点M到抛物线的准线x＝－的距离，所以点M的横坐标即点M到y轴的距离为a－.【答案】　a－[合作探究·攻重难]抛物线的方程及其几何性质　(1)设O为坐标原点，F为抛物线C：y2＝4x的焦点，P为C上一点，若PF＝4，则△POF的面积为________．(2)已知拋物线的焦点F在x轴上，直线l过F且垂直于x轴，l与拋物线交于A、B两点，O为坐标原点，若△OAB的面积等于4，求此拋物线的标准方程.[思路探究]　(1)利用抛物线的对称性及等边三角形的性质求解；(2)设出抛物线的标准方程，根据抛物线的对称性表示出三角形的面积，解方程可得抛物线方程中的参数，即得抛物线的方程．【自主解答】　(1)如图，设P(x0，y0)，由PF＝x0＋＝4，得x0＝3，代入抛物线方程得y＝4×3＝24.所以y0＝2.所以S△POF＝OF·y0＝××2＝2.【答案】　2(2)由题意，设拋物线方程为y2＝ax(a≠0)．焦点F，直线l：x＝，∴A、B两点的坐标分别为，，∴AB＝a，∵△OAB的面积为4，∴··a＝4，∴a＝±4，∴拋物线的方程为y2＝±4x.[规律方法]　1．求抛物线的标准方程时，目标就是求解p，只要列出一个关于p的方程即可求解．2．求抛物线的标准方程要明确四个步骤：n(1)定位置(根据条件确定抛物线的焦点位置及开口)；(2)设方程(根据焦点和开口设出标准方程)；(3)找关系(根据条件列出关于p的方程)；(4)得出抛物线的标准方程．[跟踪训练]1．已知双曲线C1：－＝1(a＞0，b＞0)的离心率为2，若抛物线C2：x2＝2py(p＞0)的焦点到双曲线C1的渐近线的距离为2，求抛物线C2的方程.【导学号：95902139】【解】　∵双曲线C1：－＝1(a＞0，b＞0)的离心率为2，∴＝＝2，∴b＝a，∴双曲线的渐近线方程为x±y＝c，∴抛物线C2：x2＝2py(p＞0)的焦点到双曲线的渐近线的距离为＝2，∴p＝8，∴所求的抛物线方程为x2＝16y.抛物线中的应用题　河上有抛物线型拱桥，当水面距拱顶5米时，水面宽为8米，一小船宽4米，高2米，载货后船露出水面上的部分高米，问水面上涨到与抛物线拱顶相距多少米时，小船开始不能通航？[思路探究]　→→→→【自主解答】　如图，建立坐标系，设拱桥抛物线方程为x2＝－2py(p>0)，由题意，将B(4，－5)代入方程得p＝，∴抛物线方程为x2＝－y.∵当船的两侧和拱桥接触时船不能通航．设此时船面宽为AA′，则A(2，yA)，由22＝－yA，得yA＝－.n又知船露出水面上部分为米，设水面与抛物线拱顶相距为h，则h＝|yA|＋＝2(米)，即水面上涨到距抛物线拱顶2米时，小船不能通航．[规律方法]　1．本题的解题关键是把实际问题转化为数学问题，利用数学模型，通过数学语言(文字、符号、图形、字母等)表达、分析、解决问题．2．以抛物线为数学模型的实例很多，如拱桥、隧道、喷泉等，应用抛物线主要体现在：(1)建立平面直角坐标系，求抛物线的方程．(2)利用已求方程求点的坐标．[跟踪训练]2．某隧道横断面由抛物线及矩形的三边组成，尺寸如241图所示，某卡车空车时能通过此隧道，现载一集装箱，箱宽3米，车与箱共高4.5米，问此车能否通过此隧道？说明理由.【导学号：95902140】图241【解】　建立如图所示的平面直角坐标系，则B(－3，－3)，A(3，－3)．设抛物线方程为x2＝－2py(p＞0)，将B点的坐标代入，得9＝－2p·(－3)，∴p＝，∴抛物线方程为x2＝－3y(－3≤y≤0)．∵车与箱共高4.5m，∴集装箱上表面距抛物线形隧道拱顶0.5m．设抛物线上点D的坐标为(x0，－0.5)，D′的坐标为(－x0，－0.5)，则x＝－3×(－0.5)，解得x0＝±＝±.∴|DD′|＝2|x0|＝＜3，故此车不能通过隧道.直线与抛物线的综合应用[探究问题]1．直线l过抛物线y2＝2px(p＞0)的焦点F，与抛物线交于A(x1，y1)，B(x2，y2)，则ABn的长是多少？【提示】　由抛物线的定义可知AF＝x1＋，BF＝x2＋，所以AB＝AF＋BF＝x1＋＋x2＋＝x1＋x2＋p.2．斜率为k的直线l与抛物线y2＝2px(p＞0)交于A(x1，y1)，B(x2，y2)，则AB的长是多少？【提示】　设直线l的方程为y＝kx＋m，则AB＝＝＝＝|x1－x2|.这个公式称为弦长公式．　(1)已知过抛物线y2＝6x焦点的弦长为12，则该弦所在直线的倾斜角是________．(2)求顶点在原点，焦点在x轴上且截直线2x－y＋1＝0所得弦长为的抛物线方程．[思路探究]　(1)应用焦半径公式求解；(2)应用弦长公式求解．【自主解答】　(1)抛物线的焦点为.设直线方程为y＝k，与方程y2＝6x联立得：4k2x2－(12k2＋24)x＋9k2＝0.设直线与抛物线交点为A(x1，y1)，B(x2，y2)．∴x1＋x2＝，∴x1＋x2＋3＝＋3＝12.∴k2＝1，∴k＝±1.故弦所在直线的倾斜角是或π.【答案】　或π(2)设所求抛物线方程为y2＝ax(a≠0)①直线方程变形为y＝2x＋1②设抛物线截直线得弦长为AB，将②代入①整理得4x2＋(4－a)x＋1＝0，则AB＝＝.解得a＝12或a＝－4.故所求抛物线方程为y2＝12x或y2＝－4x.[规律方法]　直线与抛物线相交的弦长问题直线和抛物线相交于A(x1，y1)，B(x2，y2)两点，直线的斜率为k.(1)一般的弦长公式：|AB|＝|x1－x2|.n(2)焦点弦长公式：当直线经过抛物线y2＝2px(p＞0)的焦点时，弦长|AB|＝x1＋x2＋p.(3)求弦长时，为简化计算常常借助根与系数的关系，这样可以避免分别求x1，x2的麻烦，如果是利用弦长求参数的问题，只需要列出参数的方程或不等式即可求解，而(x1，y2)或(y1，x2)一般是求不出来的.[跟踪训练]3．过抛物线y2＝2px(p＞0)的焦点F作倾斜角为45°的直线交抛物线于A，B两点，若线段AB的长为8，则p＝__________.【导学号：95902141】【解析】　设A(x1，y1)，B(x2，y2)，因为直线倾斜角为45°，过抛物线焦点，所以可设直线方程为y＝x－，代入抛物线方程得＝2px，即x2－3px＋＝0，故x1＋x2＝3p，由抛物线的定义可知，|AB|＝x1＋＋x2＋＝x1＋x2＋p＝4p＝8，因此p＝2.【答案】　2[构建·体系][当堂达标·固双基]1．过抛物线y2＝4x的焦点作直线与抛物线相交于P(x1，y1)，Q(x2，y2)两点，若x1＋x2＝8，则PQ的值为________.【导学号：95902142】【解析】　PQ＝x1＋x2＋2＝10.【答案】　102.如图242，已知等边三角形AOB的顶点A，B在抛物线y2＝6x上，O是坐标原点，则△AOB的边长为________．图242n【解析】　设△AOB边长为a，则A，∴＝6×a.∴a＝12.【答案】　123.如图243所示是抛物线形拱桥，当水面在1时，拱顶离水面2米，水面宽4米，水位下降1米后，水面宽________米.【导学号：95902143】图243【解析】　设水面与拱桥的一个交点为A，如图所示，建立平面直角坐标系，则A的坐标为(2，－2)．设抛物线方程为x2＝－2py(p>0)，则22＝－2p×(－2)，得p＝1.设水位下降1米后水面与拱桥的交点坐标为(x0，－3)，则x＝6，解得x0＝±，所以水面宽为2米．【答案】　24．已知点P(6，y)在抛物线y2＝2px(p＞0)上，若点P到抛物线焦点F的距离等于8，则焦点F到抛物线准线的距离等于__________．【解析】　抛物线y2＝2px(p＞0)的准线为x＝－，因为P(6，y)为抛物线上的点，所以P到焦点F的距离等于它到准线的距离，所以6＋＝8，所以p＝4，焦点F到抛物线准线的距离等于4.【答案】　45．若抛物线的顶点在原点，开口向上，F为焦点，M为准线与y轴的交点，A为抛物线上一点，且AM＝，AF＝3，求此抛物线的标准方程．【解】　设所求抛物线的标准方程为x2＝2py(p＞0)，设A(x0，y0)，由题知M.∵AF＝3，∴y0＋＝3，∵AM＝，∴x＋＝17，n∴x＝8，代入方程x＝2py0得，8＝2p，解得p＝2或p＝4.∴所求抛物线的标准方程为x2＝4y或x2＝8y.