小学数学精讲教案8_6 操作找规律 教师版

小学数学精讲教案8_6 操作找规律 教师版

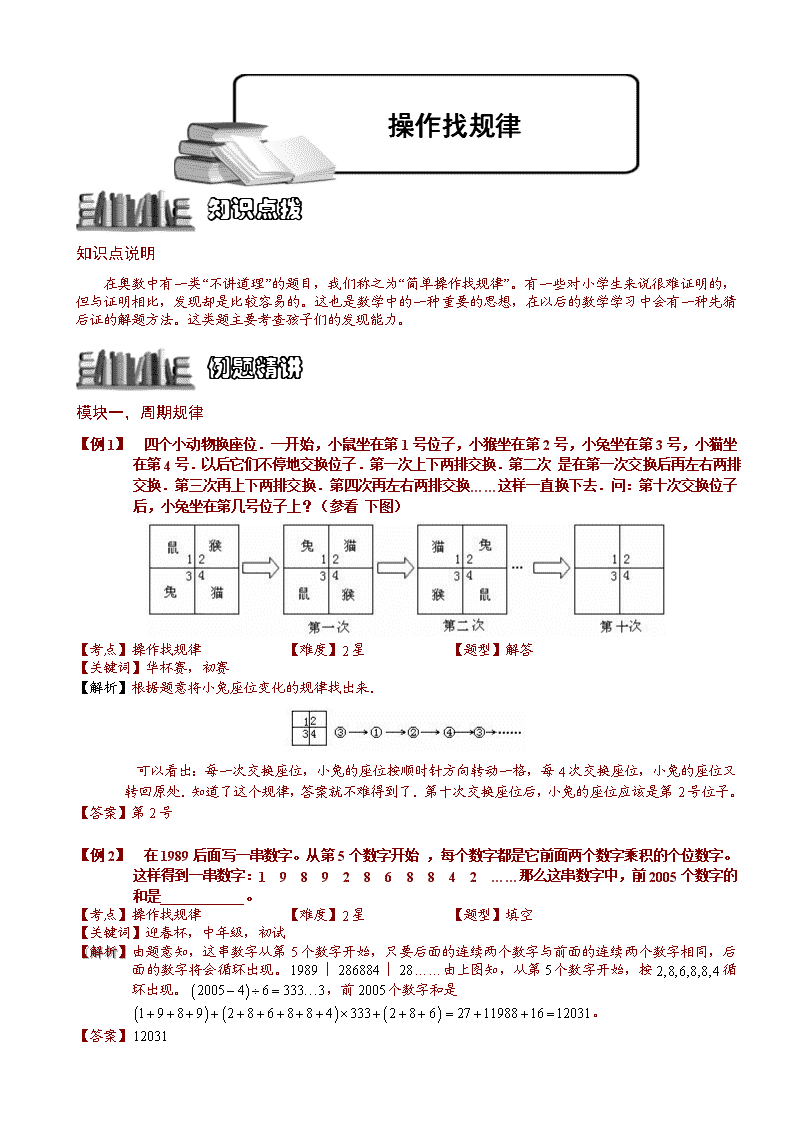
操作找规律 知识点拨 知识点说明 在奥数中有一类“不讲道理”的题目，我们称之为“简单操作找规律”。有一些对小学生来说很难证明的，但与证明相比，发现却是比较容易的。这也是数学中的一种重要的思想，在以后的数学学习中会有一种先猜后证的解题方法。这类题主要考查孩子们的发现能力。‎ 例题精讲 模块一，周期规律 【例 1】 四个小动物换座位．一开始，小鼠坐在第1号位子，小猴坐在第2号，小兔坐在第3号，小猫坐在第4号．以后它们不停地交换位子．第一次上下两排交换．第二次 是在第一次交换后再左右两排交换．第三次再上下两排交换．第四次再左右两排交换……这样一直换下去．问：第十次交换位子后，小兔坐在第几号位子上？（参看 下图）‎ ‎【考点】操作找规律 【难度】2星 【题型】解答 ‎【关键词】华杯赛，初赛 【解析】 根据题意将小兔座位变化的规律找出来．‎ 可以看出：每一次交换座位，小兔的座位按顺时针方向转动一格，每4次交换座位，小兔的座位又转回原处．知道了这个规律，答案就不难得到了．第十次交换座位后，小兔的座位应该是第2号位子。‎ ‎【答案】第2号 【例 2】 在1989后面写一串数字。从第5个数字开始 ，每个数字都是它前面两个数字乘积的个位数字。这样得到一串数字：1 9 8 9 2 8 6 8 8 4 2 ……那么这串数字中，前2005个数字的和是____________。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】迎春杯，中年级，初试 【解析】 由题意知，这串数字从第5个数字开始，只要后面的连续两个数字与前面的连续两个数字相同，后面的数字将会循环出现。︱︱……由上图知，从第个数字开始，按循环出现。，前个数字和是 ‎。‎ ‎【答案】‎ 【例 1】 先写出一个两位数62，接着在62右端写这两个数字的和8，得到628，再写末两位数字2和8的和10，得到62810，用上述方法得到一个有2006位的整数：628101123…，则这个整数的数字之和是 。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】华杯赛，决赛，第5题，10分 【解析】 该整数位6281011235813471123581347…从第6位开始，10个一循环，(2006-5)÷ 10=200…1，所以，整个整数的数字之和为：6+2+8+1+0+200×（1+1+2+3+5+8+1+3+4+7）+1=7018。‎ ‎【答案】‎ 【例 2】 有一串数1，1，2，3，5，8，…，从第三个数起，每个数都是前两个数之和，在这串数的前2009个数中，有_________个是5的倍数。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，初赛，六年级 【解析】 由于两个数的和除以5的余数等于这两个数除以5的余数之和再除以5的余数． 所以这串数除以5的余数分别为：1，1，2，3，0，3，3，1，4，0，4，4，3，2，0，2，2，4，1，0，1，1，2，3，0，…… 可以发现这串余数中，每20个数为一个循环，且一个循环中，每5个数中第五个数是5的倍数． 由于，所以前2009个数中，有401个是5的倍数．‎ ‎【答案】401个 【例 3】 小明按1~5循环报数，小花按1~6循环报数，当两个人都报了600个数时，小花报的数字之和比小明报的数字之和多________________。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】希望杯，四年级，复赛，第4题 【解析】 小花一个循环报的数字之和为：，小明一个循环报的数字之和为：，小明一共报了（组），小花一共报了（组），所以小花报的数字之和比小明报的数字之和多：。‎ ‎【答案】‎ 【例 4】 已知一列数：5，4，7，1，2，5，4，3，7，1，2，5，4，3，7，1，2，5，4，，3，……，由此可推出第2008个数是____________。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】希望杯，四年级，复赛，第8题 【解析】 观察数列发现，除前两个数字之外，，，，，，六个数字周期出现，因为，所以第个数是。‎ ‎【答案】‎ 【例 5】 ‎50名同学围成一圈做游戏：从某一个同学开始顺时针从1开始依次连续报数，报含有数字7的数（如7，17，71等）或7的倍数的同学击1次掌. 如此进行下去，当报到100时，所有同学共击掌___________次.‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】迎春杯，三年级，初赛 【解析】 含有数字或的倍数的数有类：个位为的，有，，…，；十位为的，有，，…，；的倍数有，，…，.其中有包含排除关系，根据容斥原理，～中共有()+()个，所以共击掌次.‎ ‎【答案】‎ 【例 6】 某班43名同学围成一圈。由班长起从1开始连续报数，谁报到100，谁就表演一个节目；然后再由这个同学起从1开始连续报数，结果第一个表演节目的是小明，第二个演节目的是小强。那么小明和小强之间有________名同学。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】迎春杯，中年级，初赛 【解析】 有两种情况为：或.。小明和小强之间有同学（名）或。‎ ‎【答案】或 【例 1】 二十多位小朋友围成一圈做游戏．他们依顺时针顺序从小赵报1开始连续报数，但7的倍数或带有数字7的数都要跳过去不报；报错的人表演一个节目．小明是第一个报错的人，当他右边的同学报90时他错报了91．如果他第一次报数报的是19，那么这群小朋友共有 人．‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，5年级，决赛 【解析】 a .“跳过去不报”指一个小朋友报了6，下一个小朋友不报数而是拍手，再下一个小朋友报8。此时，每个人应当轮到的数和上一次轮到的数（报出来或者拍手跳过）之间的差等于总人数。小明本次应当拍手，而不是报出91。所以，总人数是91-19=72的约数，有72，36，24，18，……，其中是“二十多”的只有24。‎ b. “跳过去不报”指一个小朋友报了6，下一个小朋友直接报8。此时，把所有7的倍数和带有数字7的数去掉之后，剩余的数字排成一列，每个人应当轮到的数和上一次轮到的数在这个数列中的位置号之差等于总人数。从19到90这72个数中，含有数字7的有27，37，47，57，67，70到79，87，共16个，是7的倍数且不含有数字7的有21，28，35，42，49，56，63，84共8个，所以排除掉之后剩下48个，总人数应当是48的约数，有48，24，16，……，其中是“二十多”的也只有24。‎ 这道题目存在两种不同的理解方式，但是答案却恰好相同，这确实是巧合。‎ ‎【答案】‎ 【例 2】 ‎50位同学围成一圈，从某同学开始顺时针报数．第一位同学报l，跳过一人第三位同学报2，跳过两人第六位同学报3，……这样下去，报到2008为止．报2008的同学第一次报的是______‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯,初赛,六年级 【解析】 将这些学生按报数方向依次编号；1、2、3、……49、50、51……2008，每一个人的编号不唯一，例如编号为2001、1951……101、51的和编号为1的为同一个人，这样第n次报数的人的编号为,报2008的同学的编号为2017036，他的最小编号为36，我们知道36=1+2+3+4+5+6+7+8，所以报2008的同学第一次报8.‎ ‎【答案】‎ 【例 3】 如果一个自然数的各位数字中有偶数个偶数，则称之为“希望数”。例如，26,201,533是希望数，8,36,208不是希望数，那么，把所有的希望树从小到大排列，第2010个希望数是____。‎ ‎【考点】操作找规律 【难度】3星 【题型】填空 ‎【关键词】希望杯，5年级，复赛，第8题 【解析】 在不进位的情况下：希望数+1=非希望数，且非希望数+1=希望数，即希望数与非希望数交替出现，因此从0~9开始，每10个数中有5个希望数，因此第2010个希望数为。‎ ‎【答案】‎ 模块二，递推规律 【例 4】 有依次排列的3个数：2，0，5，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：2，，0，5，5，这称为第一次操作，第二次同样的操作后也可产生一个新数串：2，，，2，0，5，5，0，5．继续依次操作下去．问：从新数串2，0，5开始操作，第100次后产生的那个新数串的所有数之和是多少？‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 【解析】 观察 操作次数： 开始 第一次 第二次 第三次 …‎ 总 和： 7 10 13 16 …‎ 易发现每操作一次总和增加3．因此操作100次后产生的新数串所有数之和为．‎ ‎【答案】‎ 【例 1】 对任意两个不同的自然数，将其中较大数换成这两数之差，称为一次变换．如对18和42可作这样的连续变换：18，42→18,24→18,6→12,6→6,6‎ 直到两数相同为止．问：对1234和4321作这样的连续变换最后得到的两个相同的数是 ．‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 【解析】 操作如下：1234，4321→1234，3087→1234，1853→1234，619→615，619→615，，4→3，4→3，1→2，1→1，1实际上按此法操作最后所得两相同的数为开始两数的最大公约数．即1234与4321的最大公约数为1．此法也称为辗转相减法求最大公约数．‎ ‎【答案】1‎ 【巩固】 将两个不同的自然数中较大数换成这两个数之差，称为一次操作．如对18和42可连续进行这样的操作，则有：18，42→18，24→18，6→12，6→6，．直到两数相同为止．试给出和最小的两个四位数，按照以上操作，最后得到的相同的数是15．这两个四位数是 与 ．‎ ‎【考点】操作找规律 【难度】3星 【题型】填空 【解析】 由题意，我们可以多给几组数按题目所给操作方法进行操作，从中找出规律．‎ 例如：136，63→…→1，1‎ ‎ 36，27→…→9，9‎ ‎ 84，36→…→12，12‎ 考察操作后所得结果，不难发现每次所得的最终结果是开始两数的最大公约数，因此我们只需找到两个尽量小的四位数，他们都是15的倍数，可得1005和1020．‎ ‎【答案】1005和1020‎ 【例 2】 如图，将正方形纸片由下往上对折，再由左向右对折，称为完成一次操作．按上述规则完成五次操作以后，剪去所得小正方形的左下角．问：当展开这张正方形纸片后，一共有多少个小洞孔？‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】华杯赛 【解析】 一次操作后，层数由1变为4，若剪去所得小正方形左下角，展开后只有1个小洞孔，恰是大正方形的中心．连续两次操作后，折纸层数为，剪去所得小正方形左下角，展开后在大正方形上留有(个)小洞孔．连续三次操作后，折纸层数为，剪去所得小正方形左下角，展开后大正方形留有(个)小洞孔．按上述规律不难断定：连续五次操作后，折纸层数为，剪去所得小正方形左下角，展开后大正方形纸片上共留有(个)小洞孔．‎ ‎【答案】‎ 【例 3】 如右图，一把密码锁上有25个按钮，必须将所有的按钮都按一遍才能将锁打开；而当我们按一个按钮后，只能按照这个按钮上的提示按下一个按钮。比如，当我们按第一行的第二个按钮“下2”后，按照提示“下2”，向下2格，只能按第三行的第二个按钮“左1”，接着只能按第三行的第一个按钮“下l”……为了打开这个密码锁，请你选择第一个按钮，并将这个按钮涂上阴影。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，决赛，5年级 【解析】 右2‎ ‎【答案】右2‎ 【例 1】 如左图所示，机器人从5×5方格图左上角阴影格子的中心出发，每一步都是走向与机器人所在方格有公共边的方格的中心，最终回到出发点。除去出发的方格外，机器人最多到过其它方格一次，图中的折线就是机器人走过的路径。然后我们在机器人没有到过的方格内填上数，这个数表示该方格周围的8个格子中有几个是机器人在格子内拐弯的。现在，已知在右下图所示的7×7方格图中机器人未到过的方格填上的数，请你在图中画出机器人行走的路径。‎ ‎【考点】操作找规律 【难度】3星 【题型】填空 ‎【关键词】走美杯，决赛，5年级 【解析】 ‎【答案】‎ 【例 2】 黑板上写着一个形如777…77的数，每次擦掉一个末位数，把前面的数乘以3，然后再加上刚才擦掉的数字．对所得的新数继续这样操作下去，证明：最后必获得数7．‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 【解析】 略．‎ ‎【答案】黑板上起初数是777…77，每次操作后就变出一个新数．不妨设这个数的末位数为，前面的数为，所以就是形为的数．每次操作后，黑板上就成为，它比原数少了．由此可知：⑴每次操作将使原数逐步变小；⑵如果原数能被7整除，那么所得新数仍能被7整除．所以黑板上最后必将变成7，例如当原数为777时，就有777→238→77→28→14→7‎ 【例 3】 有一副扑克牌，一开始抓若干张（小于13张），然后进行下列操作：抓和手里现有的扑克牌数目相等的扑克牌，然后若扑克牌总数超过13张，则放回其中的13张，称为一次操作。进行了777次操作后，手里有7张牌，则一开始手里有多少张？‎ ‎【考点】操作找规律 【难度】3星 【题型】填空 【解析】 根据倒退法知道第次操作后是，那么第776次操作就是：，第775次操作就是 ‎，找到规律是遇见奇数就是加后除以2，遇见偶数就是直接除以，所以操作后得到这样一串数为：、、、、、、、、、、、、、，观察发现是个一周期，所以，所以第一次手里的数是，一开始手里的数是张扑克。‎ ‎【答案】‎ 【例 1】 有20堆石子，每堆都有2006粒石子．从任意19堆中各取一粒放入另一堆，称为一次操作．经过不足20次操作后，某一堆中有石子1990粒，另一堆石子数在2080到2100之间．这一堆石子有 粒．‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，5年级，决赛 【解析】 根据题意可以得出，某一堆石子，如果被取一次，则数量减少1，如果被放入一次，则数量增加19。考虑有1990粒石子的那一堆，如果至少一次被放，则最多19次被取，最后石子数肯定不少于原来的2006粒。则该石子一次也没被放入过，则总共操作了16次。由于另一堆石子数在2008与2100之间，则只被放入过5次，被取11次，剩下石子19×5-11+2006=2090粒。‎ ‎【答案】2090粒 【例 2】 若干个硬币排成下图。每个硬币所在行的硬币数与所在列的硬币数相减得出一个差（大数或小数），如对于a，差为7-5=2。所有差的总和为（    ）。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，初赛，六年级 【解析】 找规律得102‎ ‎【答案】102‎ 【例 3】 将一个两位数的数字相乘，称为一次“操作”．如果积仍是二个两位数，重复以上操作，直到得到一个一位数．例如：(停止)共经历两次操作．一个两位数经过3次如上操作，最终得到一位数．这个两位数最小是（ ）．‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，3年级，初赛 【解析】 这个两位数最小是39，。‎ ‎【答案】‎ 【例 4】 一个特别的计算器，只有蓝、红、黄三个键．蓝键为“输入/删除”键(按它一下可输入一个数，再按它一下则将显示屏上的数删除)．每按一个红键，则显示屏上的数变为原来的2倍；每按一下黄键，则显示屏上的数的末位自动消失．现在先按蓝键输入21．‎ 请你设计一个操作过程，要求：⑴操作过程中只能按红键和黄键；⑵按键次数不超过6次；⑶最后输出的数是3．‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】小学生数学报 【解析】 略 ‎【答案】需按4次红键2次黄键，有如下操作方式：‎ ‎ ‎ 【例 1】 乒乓球从高空落下，到达地面后弹起的高度是落下高度的一半，如果乒乓球从米的高度落下，弹起后再落下，则弹起第 次时它的弹起高度不足‎1米。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，3年级，初赛 【解析】 第一次米，第二次米，第三次米，第四次米。四次时不足米。‎ ‎【答案】‎ 【例 2】 三条直线最多可以将一个正方形分割为 部分。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，3年级，初赛 【解析】 如图可知：‎ ‎1条直线最多可以讲图形分成2部分 ‎2条直线最多可以将图形分成部分 ‎3条直线最多可以将图形分成部分 以此类推可以找到N条线分平面的规律为部分。‎ ‎【答案】‎ 【例 3】 ‎24枚棋子排成三行，第一行6枚，第二行7枚，第三行11枚，每次可将一些棋子从一行移入另一行，但移动的棋子数必须等于移入那一行的棋子数，人移动三次，使每行都变成8个，把移动过程写入下表中．‎ ‎【考点】操作找规律 【难度】2星 【题型】解答 ‎【关键词】走美杯，3年级，初赛 【解析】 三行棋子初始为：‎ ‎【答案】‎ 【例 4】 如图，有一个边长为1的正三角形，第一次去掉三边中点连线围成的那个正三角形；第二次对留下的三个正三角形，再分别去掉它们中点连线围成的三角形；…做到第四次后，一共去掉了________个三角形. 去掉的所有三角形的边长之和是________.‎ ‎【考点】操作找规律 【难度】3星 【题型】填空 ‎【关键词】华杯赛，六年级，初赛，第9题 【解析】 第一次去掉1个三角形，得到3个小三角形，去掉的三角形的边长为3×； 第二次去掉3个三角形，得到9个小三角形，去掉的三角形的边长为3×3×； 第三次去掉9个三角形，得到27个小三角形，去掉的三角形的边长为9×3×； 第四次去掉27个三角形，去掉的三角形的边长为27×3×； 所以，四次共去掉1＋3＋9＋27＝40（个）小三角形， 去掉的所有三角形的边长之和是：3×＋9×＋27×＋81×＝12‎ ‎【答案】去掉个三角形，边长和是 【例 2】 观察下列正方形数表：表1中的各数之和为1，表2中的各数之和为17，表3中的各数之和为65，…（每个正方形数表比前一个正方形数表多一层方格，增加的一层方格中所填的数比前一数表的最外层方格的数大1）．如果表中的各数之和等于15505，那么等于_________．‎ ‎【考点】操作找规律 【难度】4星 【题型】填空 ‎【关键词】迎春杯，高年级，初赛 【解析】 表比表多个，也就是表的数字总和比表的数字总和大．表的数字和是．‎ 因为，‎ 所以，所以．‎ ‎【答案】‎ 【例 3】 从1999这个数里减去253以后，再加上244；然后再减去253，再加上244；……这样一直算下去，当减去第_________次时，得数恰好第一次等于0 。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】迎春杯，中年级，初赛 【解析】 ‎（次）。‎ ‎【答案】‎ 【例 4】 在左下表中，在有公共边的两格内的数同时加上1或同时减去1叫做一次操作．经过有限次操作后由左下表变为右下表，那么右下表中处的数是　 　　．‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】迎春杯，三年级，初赛 【解析】 之后两两加1操作（除去左上角的数字5）即可使余下的格内数字均为2010.所以，A处的数字是5.‎ ‎ 换成换成换成换成 换成换成换成换成 ‎【答案】5‎ 【例 1】 如果一个自然数从右往左看和从左往右看都一样，则称这个数为“回文数”。例如343，2002都是回文数。现有一个十六位数2001200220032004，请你在这个数的两端或者各位数字加加上一些数字，使它变成回文数。新得到的回文数的数字和最小是 。‎ ‎【考点】操作找规律 【难度】2星 【题型】填空 ‎【关键词】走美杯，4年级，决赛 【解析】 最小是26， 回文数中的数字是关于中心对称的。这个16位数中有5个2，1，3，4各1个，以第3个2为对称中心，再添上1，3，4各1个及若干个0，这样得到的回文数的数字和最小，是2×5+(1+3+4)×2=26。例如下面的回文数，其中箭头是对称中心，下划线上方的数字是添加的数字。‎ ‎【答案】26‎