- 2022-02-12 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版数学六年级下册 4《反比例》一课一练 (2)
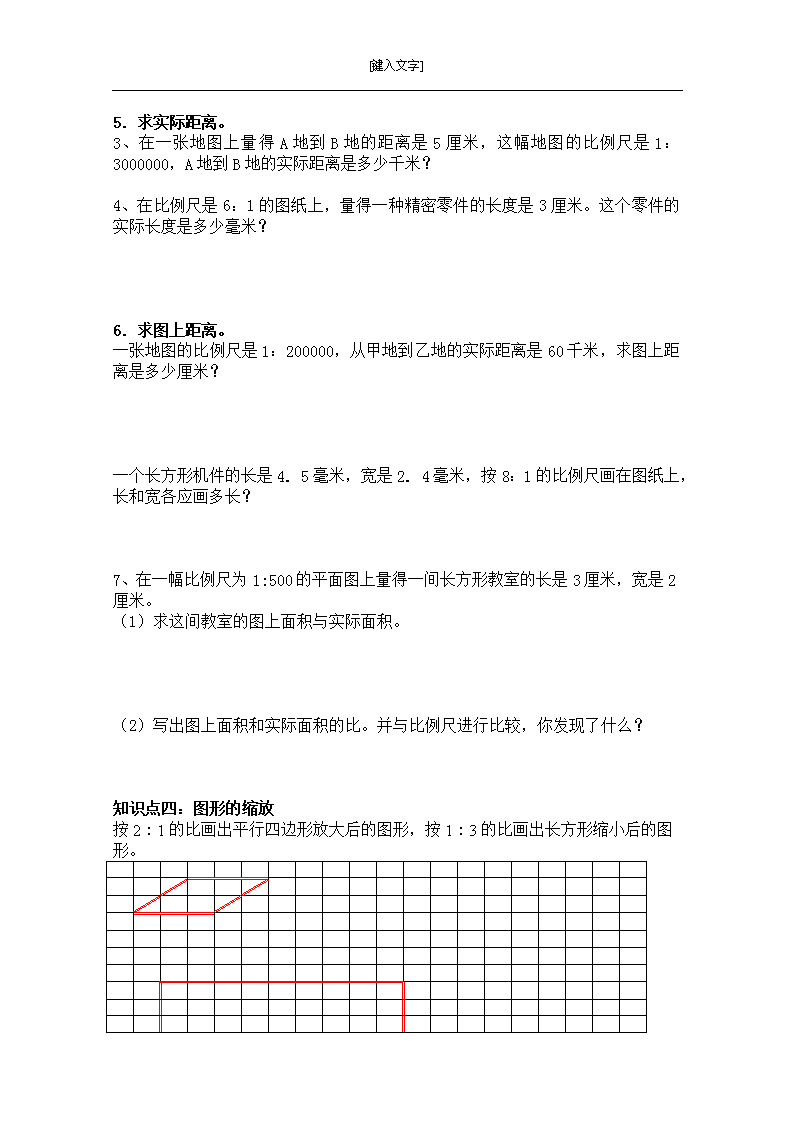
[键入文字] 比和比例章节复习 知识点一:比例的意义和基本性质: 1.表示两个比相等的式子叫做比例. 2.组成比例的四个数,叫做比例的项,两端的两项叫做比例的外项,中间的两项叫做比例的内项。 只要两个比的比值相等,就能组成比例。 比 比例 意义 两个数相除又叫做这两个数的比 表示两个比相等的式子叫做比例 构成 由两项组成,分别叫做比的前项和后项 由四项组成,两端的两项叫做比例的外项,中间的两项叫做比例的内项 基本 性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变 在比例里,两个外项的积等于两个内项的积 1.( )叫做比例。 2.( )这叫做比例的基本性质。 3.( )叫做解比例。 4.两个比的( )相等,这两个比就相等。 知识点二:正反比例的比较和应用 正比例:两种相关联的量,一种量变化,另一种量也随着变化,且这两种量中相对应的两个数的比值(或商)一定,这两种量就叫做成正比例的量,它们的关系就叫正比例关系。正比例关系用字母表示为:= k(一定)。 反比例:两种相关联的量,一种量变化,另一种量也随着变化,且这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫反比例关系。反比例关系用字母表示为:x×y = k(一定)。 正比例的图像是直线,反比例的图像是曲线。 例题讲解: 一、判断下列量是否是正反比例关系 1.如果工作时间一定,那么工作总量与工作效率成( )比例关系。 2.如果工作总量一定,那么工作时间与工作效率成( )比例关系。 3.汽车的耗油量一定,油箱中汽油的数量与行驶的路程成( )比例关系。 4.出售小麦的单价一定,出售小麦总量与总钱数成( )比例关系。 5.体操比赛的总人数一定,每排人数与排数成( )比例关系。 例2、实际应用 [键入文字] 1、一根电线,长70米,重15.4千克,现有这种电线940米,重多少千克? 2、100千克小麦可磨出面粉85千克,照这样计算,6吨小麦可以磨出面粉多少千克? 3、同学们做操,每行站15人,正好站12行。如果每行站9人,可以站多少行? 4、给一间房子铺地,如果用边长6分米的方砖,需要80块。如果改用边长8分米的方砖,需要多少块? 知识点三、比例尺 图上距离与实际距离的比,叫这幅图的比例尺。 1. 数字比例尺 如:1:3000 000 图上1厘米表示实际3000 000厘米。注意统一单位。 2. 线段比例尺 3. 比例尺的应用 比例尺的关系式: 图上距离 : 实际距离 = 比例尺 变形:图上距离 = 实际距离 × 比例尺 实际距离 = 图上距离 ÷ 比例尺 特别地:单位要统一 注意:比、比例、比例尺、百分数的后面不能带单位。 比例尺应用。 1、( )和( )的比叫做比例尺。 2、在比例尺是1:4000000的地图上,图上距离1厘米表示实际距离( )千米。也就是图上距离是实际距离的( ),实际距离是图上距离的( )倍。 3、实际距离是图上距离的50000倍,这幅设计图的比例尺是( )。 4.求比例尺。 1、在一幅地图上量得北京到武汉的距离是8厘米,而北京到武汉的实际距离是1152千米,求这幅地图的比例尺。 2、有一种精密仪器,其零件的长度是5毫米,画在图纸上的长度是8厘米,求这张图纸的比例尺。 [键入文字] 5.求实际距离。 3、在一张地图上量得A地到B地的距离是5厘米,这幅地图的比例尺是1:3000000,A地到B地的实际距离是多少千米? 4、在比例尺是6:1的图纸上,量得一种精密零件的长度是3厘米。这个零件的实际长度是多少毫米? 6.求图上距离。 一张地图的比例尺是1:200000,从甲地到乙地的实际距离是60千米,求图上距离是多少厘米? 一个长方形机件的长是4. 5毫米,宽是2. 4毫米,按8:1的比例尺画在图纸上,长和宽各应画多长? 7、在一幅比例尺为1:500的平面图上量得一间长方形教室的长是3厘米,宽是2厘米。 (1)求这间教室的图上面积与实际面积。 (2)写出图上面积和实际面积的比。并与比例尺进行比较,你发现了什么? 知识点四:图形的缩放 按2 : 1的比画出平行四边形放大后的图形,按1 : 3的比画出长方形缩小后的图形。 [键入文字] 下面的方格图中,每一个小方格表示1平方厘米,请你将一块长和宽分别是300米和200米的长方形按照1:5000的比例尺画在方格图上。 知识点五:解决实际问题: 1、修一条公路,每天修0.5千米,36天完成。如果每天修0.6千米,多少天可修完?(用比例方法解) 2、一个晒盐场用500千克海水可以晒15千克盐;照这样的计算,用100吨海水可以晒多少吨盐?(用比例方法解答) 3、 生产一批零件,计划每天生产160个,15天可以完成,实际每天超产80个,可以提前几天完成?(用比例方法解) 练习与巩固 一、填空。 2、4:10=2:5那么( )×( )=( )×( )。 3、在一个比例中,两个内项互为倒数,其中一个外项是0.25,另一个外项是( ) [键入文字] 5、Y=KX(K 一定),Y与X 是成( )的量,它们的关系叫做( )关系。 6、两个人的身高比是4:3,高个的160厘米,矮个的是( )米。 7、A牌纯净水比B牌纯净水的容量多20%,A牌纯净水与B牌纯净水容量的是最简整数比是( )。 8、数值比例尺1:6000000表示图上1厘米的距离代表实际( )千米的距离。如果实际距离是150千米,在这幅图上应画( )厘米。 二、判断。(对的画“√”,错的画“×”) 1、 0.15: 0.05和48:16可组成比例。 ( ) 2、两个圆周长的比是2:5,它们半径的比也是2:5 。( ) 3、汽车行驶的路程和所用的时间成正比例。 ( ) 4、在一幅平面图上,图上距离是3厘米表示实际距离是6米,这幅图的比例尺是1:2 . ( ) 5、等边三角形的周长和一条边长成正比例。 ( ) 三、选择。(正确答案的字母填在括号里) 1、如果6x=7y,.写成比例是( ) A、6:7=y:x B、x:y=6:7 C、6:x=7:y D、6:y=7:x 2、用3、7、9、21这四个数组成的比例式,下面的哪个式子是正确的( )。 A、21:3=7:9 B、3:7=9:21 C、9:3=7:21 D、3×21=7×9 3、下面每组的两个量中,成正比例的量有( ) A、一本童话故事书,已经看的页数和没看的页数 [键入文字] B、男学生数一定,女学生数和全班人数 C、一袋大米,已经吃了的和没吃的 D、圆的周长和直径 4、下面每组中的两个量中,成反比例的量有( ) A、圆的周长和圆周率 B、如果A× =4× 那么A和B C、一个三角形的面积是5平方厘米,它的底和高 D、房间面积一定,铺地方砖的面积和所需块数 四、解比例。 (1)0.4:0.8=9:x (2)0.24 :x=4: 1.5 (3)8.4:1.4=x: 1.2 五、应用题。 1、在比例尺是1:6000000的地图上,量得甲乙两个火车站的距离是2.4厘米。求甲乙两个车站的实际距离是多少千米? 2、在某城市的公交路线图上,2路公交车从火车站到终点站的实际距离是20千米,已知这幅图的比例尺是1:50000 ,从火车站到终点站的图上距离是多少厘米? [键入文字] 3、学校班车4分钟行驶了2400米,照这样的速度,从第1站到学校共行驶了30分钟,这段路程有多少千米?(解比例) 4、为了预防冬季感冒,校医室按1:200的配比配制了消毒液。现在有2瓶105毫升的药液,需要加入多少升水? 5、用同样的地砖铺地,铺完36平方米的房间用了方砖180块地砖,如果再铺个48平方米的房间,还要用地砖多少砖?(用比例解) 6运一批药品,每箱装36瓶,需要40只箱子。如果每箱24瓶,需要多少只箱子?(用比例解) 7、面积相等的两块长方形试验田,一块长150米,宽45米,另一块长112.5米,宽是多少米?(用比例解) 课后巩固: 一、我会判断。(对的画 √ ,错的画 × ,) 1、比例尺只有数值比例尺。( ) 2、如果4b=5a,那么a:b=4:5 ( ) 3、两个比可以组成一个比例。 ( ) 4、在比例里,两个内项和外项的积的比值一定是1。 ( ) 5、分数值一定,分子和分母成正比例关系。 ( ) [键入文字] 6、比的前项和后项同时乘上同一个数,比值不变。 ( ) 二、我会选。 7、把线段比例尺 改写成数值比例尺是( )。 A、 B、 C、 D、 8、表示c和a成反比例关系的式子是( )。 A、c+a=0 B、ca=15 C、c=a 9、两个正方形的棱长之比是1 :2,那么,它们的体积之比是( )。 A、1∶2 B、1∶4 C、1∶8 D、1∶16 10、甲数比乙数多80%,乙数与甲数的比是( )。 A、5∶4 B、4∶5 C、9∶5 D、5∶9 三、解比例我最行。 1、 2、 3、 四、我会画。 先按2:1的比画出三角形和梯形放大后的图形,再按1:2的比画出平行四边形缩小后的图形。 五、解决问题我最行。 1、在比例尺是 的中国地图上量得北京到上海的距离是4.2厘米.北京到上海的实际距离大约是多少千米? [键入文字] 2、一个修路队,原来计划每天修400米,15天可以完成任务.结果12天完成任务,实际每天修多少米?(5分) 3、一种农药,用药液和水按照2∶500配制而成。5千克药液能配制这种农药多少千克?(5分) 5、食堂里的一批煤,如果每天烧0.6吨,可以烧24天;如果每天少烧0.12吨,这批煤可以烧多少天?(两种方法解答) 查看更多