- 2022-02-12 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级下册数学试题-小升初专题培优:染色与覆盖(含答案)全国通用
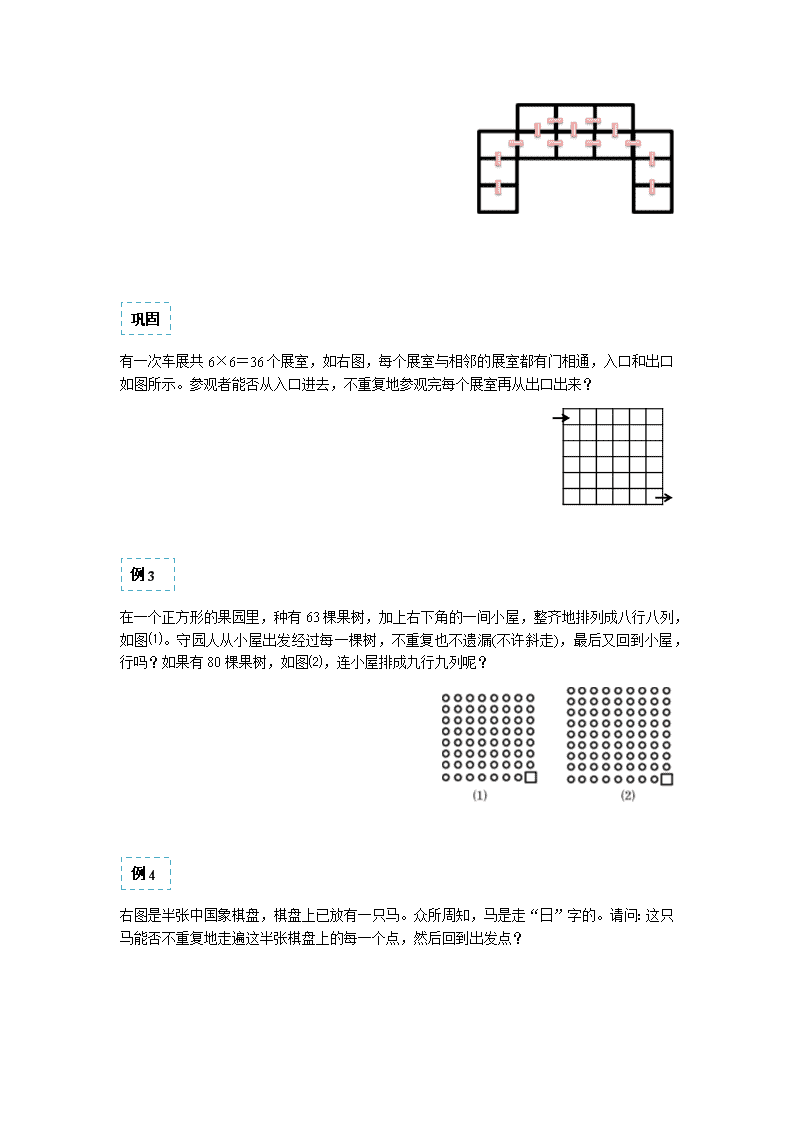
染色与覆盖 染色问题 这里的染色问题不是要求如何染色,然后问有多少种染色方法的那类题目,它指的是一种解题方法。染色方法是一种将题目研究对象分类的形象化方法,通过将问题中的对象适当染色,我们可以更形象地观察分析出其中所蕴含的关系,再经过一定的逻辑推理,便能得出问题的答案。这类问题不需要太多的数学知识,但技巧性,逻辑性较强,要注意学会几种典型的染色问题。 例1 六年级一班全班有35名同学,共分成5排,每排7人,坐在教室里,每个座位的前后左右四个位置都叫做它的邻座。如果要让这35名同学各人都恰好坐到他的邻座上去,能办到吗?为什么? 巩固 右图是某一湖泊的平面图,图中所有曲线都是湖岸。 ⑴如果P点在岸上,那么A点是在岸上还是在水中? ⑵某人过此湖泊,他下水时脱鞋,上岸时穿鞋。如果他从A点出发走到某点B,他穿鞋与脱鞋的总次数是奇数,那么B点是在岸上还是在水中?为什么? 例2 右图是某一套房子的平面图,共12个房间,每相邻两房间都有门相通。请问:你能从某个房间出发,不重复地走完每个房间吗? 巩固 有一次车展共6×6=36个展室,如右图,每个展室与相邻的展室都有门相通,入口和出口如图所示。参观者能否从入口进去,不重复地参观完每个展室再从出口出来? 例3 在一个正方形的果园里,种有63棵果树,加上右下角的一间小屋,整齐地排列成八行八列,如图⑴。守园人从小屋出发经过每一棵树,不重复也不遗漏(不许斜走),最后又回到小屋,行吗?如果有80棵果树,如图⑵,连小屋排成九行九列呢? 例4 右图是半张中国象棋盘,棋盘上已放有一只马。众所周知,马是走“日”字的。请问:这只马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点? 例5 右图是由14个大小相同的方格组成的图形。试问能不能剪裁成7个由相邻两方格组成的长方形? 巩固 下图是由40个小正方形组成的图形,能否将它剪裁成20个相同的长方形? 例6 用11个和5个能否盖住8×8的大正方形? 巩固 用若干个2×2和3×3的小正方形能不能拼成一个11×11的大正方形,请你说明理由! 测试题 1.某班有45名同学按9行5列坐好.老师想让每位同学都坐到他的邻座(前后左右)上去,问这能否办到? 2.下面的三个图形都是从4×4的正方形纸片上剪去两个1×1的小方格后得到的. 问:能否把它们分别剪成1×2的七个小矩形? 3.能否用9个所示的卡片拼成一个6×6的棋盘? 4.一个正方形果园里种有48棵果树,加上右下角的一间小屋,整齐地排列成七行七列(见图)。守园人从小屋出发经过每一棵树,不重复也不遗漏(不许斜走),最后又回到小屋可以做到吗? 5.如图,缺两格的8×8方格有62个格,能否用31个图不重复地盖住它且不留空隙? 答案 1.答案:不能,我们将9行5列染色,黑色座位和白色座位成了邻座,黑色座位坐到白色座位上,白色座位坐到黑色座位上。所以黑色格子的数目等于白色格子的数目,但实际黑格有23个,白格有22个,23≠22,所以不能办到。 2.答案:如上图⑴可以,黑白格相同;⑵、⑶不可以,黑白格不同。而1×2的矩形盖住的黑格数=白格数。 3.答案:不能,因为每个必盖住1个白格3个黑格或1个黑格3个白格,9个盖住的白格和黑格数都是奇数,实际6×6的棋盘染色后黑格数=白格数,所以不能拼成。 4.答案:将上图黑白相间的染色,每次只能从到,或到。不重复的走完所有,并回到原点,起点和终点都是,所以和一样多,但有25个,24个,所以不可以做到。 5.答案:如图黑格有30个,白格有32个,但每个盖住1个黑格、1个白格,所以31个盖住31个黑格、31个白格,所以不能不重复地盖住它且不留空隙。查看更多