人教A版 高中数学 必修2 第三章：直线与方程 测试（含答案）

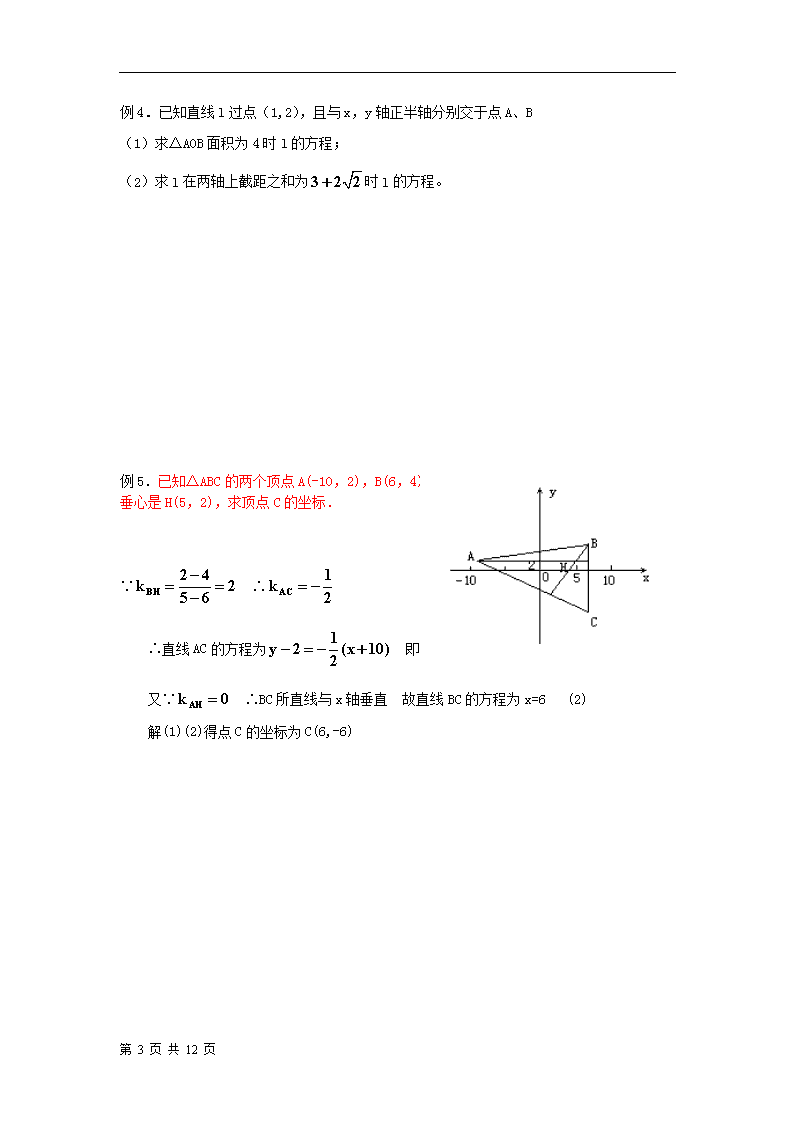
人教A版 高中数学 必修2 第三章：直线与方程 测试（含答案）

第三单元测试（4）‎ 一、知识要点:‎ ‎1. 倾斜角与斜率 ‎2. 直线方程式的5种形式:点斜式、斜截式、两点式、截距式、一般式（注意用前四种方程的条件及一般式与其它形式转化的条件）‎ ‎3．两条直线平行、垂直的条件(与斜率及系数的关系)‎ ‎4．距离公式：两点间的距离公式、点到直线的距离公式、两平行直线间的距离公式 ‎5. 对称问题(点对称、轴对称)‎ 二、基础知识练习：‎ ‎1. 直线倾斜角的取值范围___________,直线斜率的定义公式_____________, 过两点P1(x1,y1), P2(x2,y2)的斜率公式______________,斜率的取值范围______________.‎ ‎2．x=1的倾斜角为__________,直线的倾斜角是__________,时的斜率_________.‎ ‎3. 直线方程的点斜式方程_________________,直线方程的斜截式方程_________________,直线方程的两点式方程_________________,直线方程的截距式方程_________________,直线方程的一般式方程_______________,与x轴垂直的直线方程___________,与y轴垂直的直线方程___________.‎ ‎4.已知直线,若∥,则__________________,若⊥,则______________;已知直线,若∥,则_________________,若、重合,则__________________,若⊥,则______________.‎ ‎5. 与平行的直线可设为______________,与垂直的直线可设为____________________.‎ ‎6.直线当过原点O时,的取值分别是 ;‎ 当轴且相距为5时,的取值分别为 .‎ ‎7.若三点共线,则的值为 .‎ ‎8. 平面上任意两点 的距离公式__________________________,‎ 点到直线的距离d=_________________,两条平行直线与间的距离为d=________________.‎ ‎9. 过点，且在两坐标轴上截距相等的直线方程是_________________．‎ 第 12 页 共 12 页 ‎ ‎10.两平行直线3x+4y-12=0和6x+8y+6=0间的距离是________________.‎ 三、典例解析 例1.下列命题正确的有 :‎ ‎①每条直线都有唯一一个倾斜角与之对应,也有唯一一个斜率与之对应;‎ ‎②倾斜角的范围是:0°≤α<180°,且当倾斜角增大时,斜率也增大;‎ ‎③过两点A(1,2),B(m,-5)的直线可以用两点式表示;‎ ‎④过点(1,1),且斜率为1的直线的方程为;‎ ‎⑤直线Ax+By+C=0(A,B不同时为零),当A,B,C中有一个为零时,这个方程不能化为截距式.‎ ‎⑥若两直线平行,则它们的斜率必相等;‎ ‎⑦若两直线垂直,则它们的斜率相乘必等于-1.‎ 例2.若直线与直线，则时，a_________;时，a=__________;这时它们之间的距离是________;时，a=________ .‎ 例3．求满足下列条件的直线方程：‎ ‎(1)经过点P(2，-1)且与直线2x+3y+12=0平行；‎ ‎(2)经过点Q(-1，3)且与直线x+2y-1=0垂直；‎ ‎(3)经过点R(-2，3)且在两坐标轴上截距相等；‎ ‎(4)经过点M(1，2)且与点A(2,3)、B(4,-5)距离相等；‎ ‎(5) 经过点N(-1,3)且在轴的截距与它在y轴上的截距的和为零.‎ 第 12 页 共 12 页 ‎ 例4．已知直线l过点（1,2），且与x，y轴正半轴分别交于点A、B ‎（1）求△AOB面积为4时l的方程；‎ ‎（2）求l在两轴上截距之和为时l的方程。 ‎ 例5．已知△ABC的两个顶点A(-10，2)，B(6，4)，‎ 垂心是H(5，2)，求顶点C的坐标． ‎ ‎∵ ∴‎ ‎∴直线AC的方程为 即x+2y+6=0 (1)‎ 又∵ ∴BC所直线与x轴垂直 故直线BC的方程为x=6 (2)‎ 解(1)(2)得点C的坐标为C(6,-6)‎ 第 12 页 共 12 页 ‎ 四、练习巩固 ‎ ‎1．直线L：ax+4my+3a=0 (m≠0)过点(1 , -1)，那么L的斜率为 （ ）‎ A． B．-4 C． - D．4 ‎ ‎2．两平行直线分别过（1，5），（－2，1）两点，设两直线间的距离为d，则 （ ）‎ ‎ A．d=3 B．d=4 C．3≤d≤4 D．00‎ O A B ‎(1,2)‎ x y ‎ ∴l的方程为 ∵点（1,2）在直线上 ‎ ∴ ∴ ① ∵b>0 ∴a>1 ‎ ‎ (1) S△AOB== =4 ‎ ‎ ∴a=2 这时b=4 ∴当a=2，b=4时S△AOB为4‎ 第 12 页 共 12 页 ‎ ‎ 此时直线l的方程为即2x+y-4=0‎ ‎ (2) ∴ 这时 ‎ ∴l在两轴上截距之和为3+2时，直线l的方程为y=-x+2+。‎ 例5．解: ∵ ∴‎ ‎∴直线AC的方程为 即x+2y+6=0 (1)‎ 又∵ ∴BC所直线与x轴垂直 故直线BC的方程为x=6 (2)‎ 解(1)(2)得点C的坐标为C(6,-6)‎ 四、练习巩固 ‎1．C 2. D 3. C 4. C 5. D ‎6.x=5或3x-4y+25=0 7. 8.(-∞,-1)∪(1,+ ∞) 9. ‎ ‎10. 解：设 则当y=0得 ; 则当x=0得 ‎∵直线l与两坐标轴围成的三角形面积为24‎ ‎∴ ∴‎ ‎∴直线l的方程为 ‎11. 解：（１）由题意得：‎ 即，解之得　．‎ ‎（２）由题意得：‎ ‎，‎ 即，解之得　．‎ 直线与方程之综合应用答案 二、典例解析 例1．解：（方法一）设过点的直线的方程为，则，∴‎ 第 12 页 共 12 页 ‎ ‎，‎ 由逐步试解可得或，所以选B.‎ ‎（方法二）设过点的直线的方程为，则 由得：或，相应的由或，所以选B.‎ 例2．解：依题意得：，这说明在直线上，同理，也在直线上．‎ ‎　　　因为两点确定一直线，所以经过两点、的直线方程为．‎ 例3．设关于直线的对称点为 则 解得 ‎∴直线的方程为 即 故直线的方程为 例4．解：过点B（0，3）且与直线垂直的直线方程为，‎ ‎ 由得： ，即直线与直线相交于点，‎ ‎ 点B（0，3）关于点的对称点为，‎ ‎ 连，则依平面几何知识知，与直线的交点P即为所求。‎ 第 12 页 共 12 页 ‎ ‎ 直线的方程为，由得，即：,‎ ‎ 相应的最小值为.‎ 例5．解: 与两平行直线等距离的直线方程为 解得交点 则所求直线的方程为 即 三、练习巩固 ‎1. C 2. B 3. D 4. A 5. D ‎ ‎6. C解：，当时，，故舍去；‎ ‎ ，当时，，故舍去；‎ ‎. 综上所述：‎ ‎7. 3x-y+3=0 ‎ ‎8. (解：直线l过定点(-1,-3)，数形结合得，，∴，解之得：.)‎ ‎9. 5 10. 11. (10,-15)‎ ‎12. 解：直线AB的斜率为2，∴AB边所在的直线方程为，‎ ‎ 直线AB与AC边中线的方程交点为 ‎ 设AC边中点D(x1，3－2x1)，C(4－2y1，y1)，∵D为AC的中点，由中点坐标公式得 ‎ 边所在的直线方程为；‎ ‎ AC边所在的直线方程为y＝1．‎ 第 12 页 共 12 页 ‎ ‎13. 解：点O（0，0）关于直线的对称点为，直线的方程为，直线与直线的交点即为所求，相应的的最大值为 高考资源网(www.ks5u.com)‎ www.ks5u.com 来源：高考资源网 版权所有：高考资源网(www.k s 5 u.com)‎ 版权所有：高考资源网(www.ks5u.com)‎ 版权所有：金太阳新课标资源网( http://wx.jtyjy.com/)‎ 第 12 页 共 12 页 ‎