- 2022-02-12 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
小学数学精讲教案5_4_4 完全平方数及应用(一) 教师版
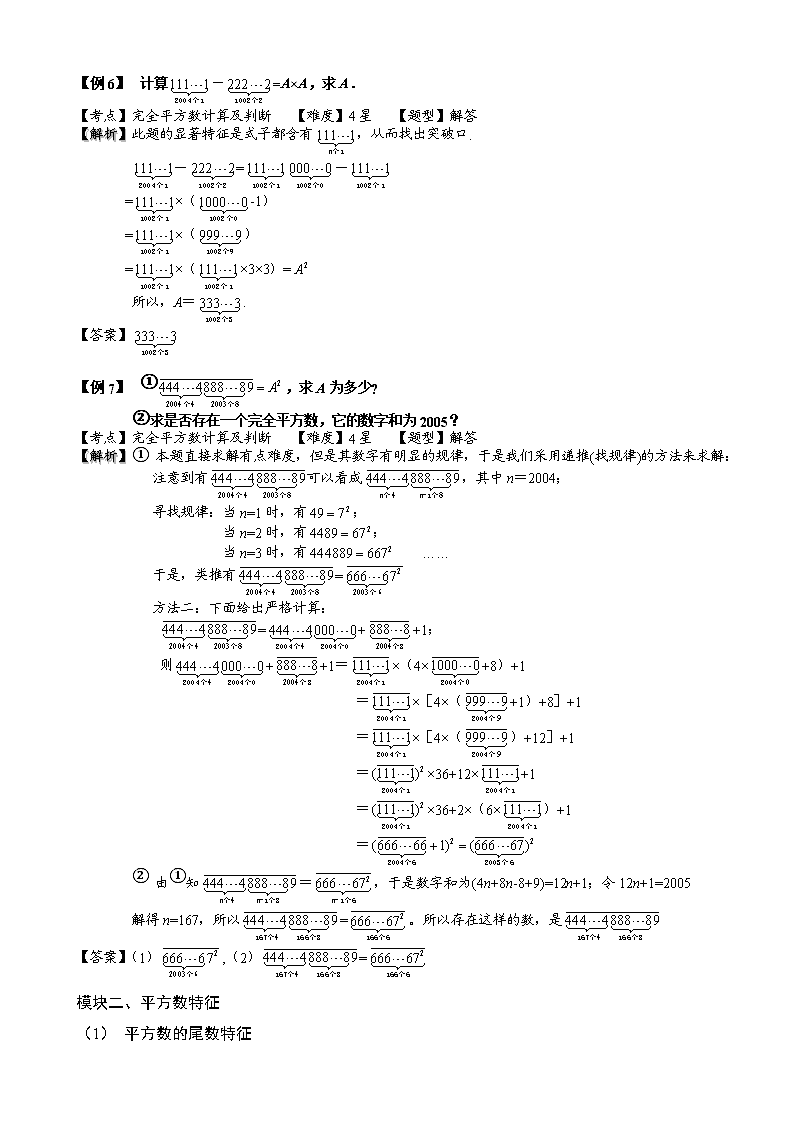
5-4-4.完全平方数及应用(一) 教学目标 1. 学习完全平方数的性质; 2. 整理完全平方数的一些推论及推论过程 3. 掌握完全平方数的综合运用。 知识点拨 一、完全平方数常用性质 1.主要性质 1.完全平方数的尾数只能是0,1,4,5,6,9。不可能是2,3,7,8。 2.在两个连续正整数的平方数之间不存在完全平方数。 3.完全平方数的约数个数是奇数,约数的个数为奇数的自然数是完全平方数。 4.若质数p整除完全平方数,则p能被整除。 2.性质 性质1:完全平方数的末位数字只可能是0,1,4,5,6,9. 性质2:完全平方数被3,4,5,8,16除的余数一定是完全平方数. 性质3:自然数N为完全平方数自然数N约数的个数为奇数.因为完全平方数的质因数分解中每个质因数出现的次数都是偶数次,所以,如果p是质数,n是自然数,N是完全平方数,且,则. 性质4:完全平方数的个位是6它的十位是奇数. 性质5:如果一个完全平方数的个位是0,则它后面连续的0的个数一定是偶数.如果一个完全平方数的个位是5,则其十位一定是2,且其百位一定是0,2,6中的一个. 性质6:如果一个自然数介于两个连续的完全平方数之间,则它不是完全平方数. 3.一些重要的推论 1.任何偶数的平方一定能被4整除;任何奇数的平方被4(或8)除余1.即被4除余2或3的数一定不是完全平方数。 2.一个完全平方数被3除的余数是0或1.即被3除余2的数一定不是完全平方数。 3.自然数的平方末两位只有:00,01,21,41,61,81,04,24,44,64,84,25,09,29,49,69,89,16,36,56,76,96。 4.完全平方数个位数字是奇数(1,5,9)时,其十位上的数字必为偶数。 5.完全平方数个位数字是偶数(0,4)时,其十位上的数字必为偶数。 6.完全平方数的个位数字为6时,其十位数字必为奇数。 7.凡个位数字是5但末两位数字不是25的自然数不是完全平方数;末尾只有奇数个“0”的自然数不是完全平方数;个位数字为1,4,9而十位数字为奇数的自然数不是完全平方数。 3.重点公式回顾:平方差公式: 例题精讲 模块一、完全平方数计算及判断 【例 1】 已知:1234567654321×49是一个完全平方数,求它是谁的平方? 【考点】完全平方数计算及判断 【难度】2星 【题型】解答 【解析】 我们不易直接求解,但是其数字有明显的规律,于是我们采用递推(找规律)的方法来求解:121=;12321=;1234321=……,于是,我们归纳为1234…n…4321=,所以,1234567654321:11111112;则,1234567654321×49=11111112×72=77777772.所以,题中原式乘积为7777777的平方. 【答案】7777777 【例 1】 是 的平方. 【考点】完全平方数计算及判断 【难度】2星 【题型】填空 【关键词】祖冲之杯 【解析】 ,, 原式. 【答案】7777777 【例 2】 已知自然数满足:除以得到一个完全平方数,则的最小值是 。 【考点】完全平方数计算及判断 【难度】3星 【题型】填空 【关键词】学而思杯,6年级,第9题 【解析】 (法1)先将!分解质因数:,由于除以得到一个完全平方数,那么这个完全平方数是的约数,那么最大可以为,所以最小为。 (法2)除以得到一个完全平方数,的质因数分解式中、、的幂次是奇数,所以的最小值是。 【答案】 【例 3】 有一个正整数的平方,它的最后三位数字相同但不为0,试求满足上述条件的最小的正整数. 【考点】完全平方数计算及判断 【难度】3星 【题型】解答 【解析】 平方数的末尾只能是0,1,4,5,6,9,因为111,444,555,666,999都不是完全平方数,所以所求的数最小是4位数.考察1111,1444……可以知道,所以满足条件的最小正整数是. 【答案】1444 【例 4】 A是由2002个“4”组成的多位数,即,A是不是某个自然数B的平方?如果是,写出B;如果不是,请说明理由. 【考点】完全平方数计算及判断 【难度】3星 【题型】解答 【解析】 略 【答案】.如果A是某个自然数的平方,则也应是某个自然数的平方, 并且是某个奇数的平方.由奇数的平方除以4的余数是1知,奇数的平方减1应是4的倍数, 而不是的倍数,矛盾,所以A不是某个自然数的平方. 【巩固】 是由2008个“4”组成的多位数,即,是不是某个自然数的平方?如果是,写出;如果不是,请说明理由. 【考点】完全平方数计算及判断 【难度】3星 【题型】解答 【解析】 略 【答案】不是.假设是某个自然数的平方,则也应是某个自然数的平方,并且是某个奇数的平方.由奇数的平方除以4的余数是1知,奇数的平方减1应是4的倍数,而不是4的倍数,与假设矛盾.所以不是某个自然数的平方. 【例 5】 计算-=A×A,求A. 【考点】完全平方数计算及判断 【难度】4星 【题型】解答 【解析】 此题的显著特征是式子都含有,从而找出突破口. -=- =×(-1) =×() =×(×3×3)= 所以,A=. 【答案】 【例 1】 ①,求A为多少? ②求是否存在一个完全平方数,它的数字和为2005? 【考点】完全平方数计算及判断 【难度】4星 【题型】解答 【解析】 ① 本题直接求解有点难度,但是其数字有明显的规律,于是我们采用递推(找规律)的方法来求解: 注意到有可以看成,其中n=2004; 寻找规律:当n=1时,有; 当n=2时,有; 当n=3时,有 …… 于是,类推有= 方法二:下面给出严格计算: =++1; 则++1=×(4×+8)+1 =×[4×(+1)+8]+1 =×[4×()+12]+1 =×36+12×+1 =×36+2×(6×)+1 = ② 由①知=,于是数字和为(4n+8n-8+9)=12n+1;令12n+1=2005 解得n=167,所以=。所以存在这样的数,是 【答案】(1),(2)= 模块二、平方数特征 (1) 平方数的尾数特征 【例 2】 下面是一个算式:,这个算式的得数能否是某个数的平方? 【考点】平方数特征之平方数的尾数特征 【难度】3星 【题型】解答 【关键词】华杯赛 【解析】 判断一个数是否是某个数的平方,首先要观察它的个位数是多少.平方数的个位数只能是0,1,4,5,6,9,而2,3,7,8不可能是平方数的个位数. 这个算式的前二项之和为3,中间二项之和的个位数为0,后面二项中每项都有因子2和5,个位数一定是0,因此,这个0算式得数的个位数是3,不可能是某个数的平方. 【答案】不是 【例 1】 一个数与它自身的乘积称为这个数的平方.各位数字互不相同且各位数字的平方和等于49的四位数共有________个. 【考点】平方数特征之平方数的尾数特征 【难度】4星 【题型】填空 【关键词】学而思杯,5年级,第10题 【解析】 ,全排列共有个。 【答案】 【例 2】 用1~9这9个数字各一次,组成一个两位完全平方数,一个三位完全平方数,一个四位完全平方数.那么,其中的四位完全平方数最小是 . 【考点】平方数特征之平方数的尾数特征 【难度】5星 【题型】填空 【关键词】迎春杯,高年级,复试,11题 【解析】 四位完全平方数≥1234>352=1225,所以至少是362=1296.当四位完全平方数是1296时,另两个平方数的个位只能分别为4,5,个位为5的平方数的十位只能是2,但数字2在1296中已经使用.当四位完全平方数是372=1369时,另两个平方数的个位只能分别为4,5,个位为5的平方数的十位一样只能是2,还剩下7,8,而784恰好为282.所以,其中的四位完全平方数最小是1369. 【答案】 【例 3】 称能表示成1+2+3+…+K的形式的自然数为三角数,有一个四位数N,它既是三角数,又是完全平方数,N= 。 【考点】平方数特征之平方数的尾数特征 【难度】5星 【题型】填空 【关键词】走美杯,初赛,六年级,第14题 【解析】 N=k×(1+k)/2=m^2,4位数的话 2000<=k×(k+1)<20000, 45<=k<=140,k=2n n*(2n+1)=N。 n与2n+1 互质 ,所以要均为平方数。平方数末尾149650。满足要求的是4950。 23<=n<=70 发现没有:k=2n-1, n×(2n-1)=N 同上,满足要求是1650找到25 所以 k=49, N=1225, m=35。 【答案】 (1) 奇数个约数——指数是偶数 【例 4】 在,,,,,……等这些算是中,4,9,16,25,36,……叫做完全平方数。那么,不超过2007的最大的完全平方数是_________。 【考点】平方数特征之奇数个约数 【难度】2星 【题型】填空 【关键词】希望杯,四年级,复赛,第4题,5分 【解析】 45×45=2025;44×44=1936,所以最大的是1936. 【答案】 【例 5】 写出从360到630的自然数中有奇数个约数的数. 【考点】平方数特征之奇数个约数 【难度】2星 【题型】解答 【解析】 一个合数的约数的个数是在严格分解质因数之后,将每个质因数的指数(次数)加1后所得的乘积.如:1400严格分解质因数后为23×52×7,所以它的约数有(3+1)×(2+1)×(1+1)=4×3×2=24个.(包括1和它自身) 如果某个自然数有奇数个约数,那么这个数的所有质因子的个数均为偶数个.这样它们加1后均是奇数,所得的乘积才能是奇数.而所有质因数的个数均是偶数个的数为完全平方数.即完全平方数(除0外)有奇数个约数,反过来,有奇数个约数的数一定是完全平方数. 由以上分析知,我们所求的为360~630之间有多少个完全平方数? 18×18=324,19×19=361,25×25=625,26×26=676,所以在360~630之间的完全平方数为192,202,212,222,232,242,252. 即360到630的自然数中有奇数个约数的数为361,400,441,484,529,576,625. 【答案】361,400,441,484,529,576,625 【例 1】 1016与正整数a的乘积是一个完全平方数,则a的最小值是________. 【考点】平方数特征之奇数个约数 【难度】2星 【题型】填空 【解析】 先将1016分解质因数:,由于是一个完全平方数,所以至少为,故a最小为. 【答案】254 【巩固】 已知恰是自然数b的平方数,a的最小值是 。 【考点】平方数特征之奇数个约数 【难度】2星 【题型】填空 【解析】 ,要使是某个自然数的平方,必须使各个不同质因数的个数为偶数,由于其中质因子3和7各有2个,质因子2有3个,所以为2可以使是完全平方数,故至少为2. 【答案】2 【例 2】 从1到2008的所有自然数中,乘以72后是完全平方数的数共有多少个? 【考点】平方数特征之奇数个约数 【难度】3星 【题型】解答 【解析】 完全平方数,其所有质因数必定成对出现. 而,所以满足条件的数必为某个完全平方数的2倍, 由于,所以、、……、都满足题意,即所求的满足条件的数共有31个. 【答案】31 【例 3】 已知自然数满足:除以得到一个完全平方数,则的最小值是 。 【考点】平方数特征之奇数个约数 【难度】3星 【题型】填空 【关键词】学而思杯,6年级 【解析】 (法1)先将!分解质因数:,由于除以得到一个完全平方数,那么这个完全平方数是的约数,那么最大可以为,所以最小为。 (法2)除以得到一个完全平方数,的质因数分解式中、、的幂次是奇数,所以的最小值是。 【答案】231 【例 4】 有5个连续自然数,它们的和为一个平方数,中间三数的和为立方数,则这五个数中最小数的最小值为 . 【考点】平方数特征之奇数个约数 【难度】4星 【题型】填空 【解析】 考查平方数和立方数的知识点,同时涉及到数量较少的连续自然数问题,设未知数的时候有技巧:一般是设中间的数,这样前后的数关于中间的数是对称的. 设中间数是x,则它们的和为, 中间三数的和为.是平方数,设,则,是立方数,所以至少含有3和5的质因数各2个, 即至少是225,中间的数至少是1125,那么这五个数中最小数的最小值为1123. 【答案】1123 【例 5】 求一个最小的自然数,它乘以2后是完全平方数,乘以3后是完全立方数,乘以5后是5次方数. 【考点】平方数特征之奇数个约数 【难度】4星 【题型】解答 【解析】 为使所求的数最小,这个数不能有除2、3、5之外的质因子.设这个数分解质因数之后为,由于它乘以2以后是完全平方数,即是完全平方数,则、、都是2的倍数; 同理可知、、是3的倍数,、、是5的倍数. 所以,是3和5的倍数,且除以2余1;是2和5的倍数,且除以3余2;是2和3的倍数,且除以5余4.可以求得、、的最小值分别为15、20、24,所以这样的自然数最小为. 【答案】 【例 1】 三个连续正整数,中间一个是完全平方数,将这样的三个连续正整数的积称为“美妙数”.问:所有小于2008的美妙数的最大公约数是多少? 【考点】平方数特征之奇数个约数 【难度】4星 【题型】解答 【关键词】华杯赛 【解析】 是一个美妙数,因此美妙数的最大公约数不会大于60.任何三个连续正整数,必有一个能为3整除,所以,任何美妙数必有因子3.若中间的数是偶数,它又是完全平方数,必定能为4整除;若中间的数是奇数,则第一和第三个数是偶数,所以任何美妙数必有因子4.另外,由于完全平方数的个位数字只能是0,1,4,5,6,9,若其个位是0和5,则中间的数能被5整除;若其个位是1和6,则第一个数能被5整除;若其个位是4和9,则第三个数能被5整除.所以,任何美妙数必有因子5.由于3,4,5的最小公倍数是60,所以任何美妙数必有因子60,故所有美妙数的最大公约数至少是60.综合上面分析,所有美妙数的最大公约数既不能大于60,又至少是60,所以,只能是60. 【答案】60 【例 2】 考虑下列32个数:,,,……,,请你去掉其中的一个数,使得其余各数的乘积为一个完全平方数,划去的那个数是 . 【考点】平方数特征之奇数个约数 【难度】4星 【题型】填空 【解析】 设这32个数的乘积为A. , 所以,只要划去这个数,即可使得其余各数的乘积为一个完全平方数. 另外,由于,而16也是完全平方数,所以划去也满足题意. 【答案】或,答案不唯一 【例 3】 一个数的完全平方有39个约数,求该数的约数个数是多少? 【考点】平方数特征之奇数个约数 【难度】4星 【题型】解答 【解析】 设该数为,那么它的平方就是, 因此. 由于, ⑴所以,,,可得,; 故该数的约数个数为个; ⑵或者,,可得,那么该数的约数个数为个. 所以这个数的约数个数为14个或者20个. 【答案】14个或者20个 【例 4】 有一个不等于0的自然数,它的是一个立方数,它的是一个平方数,则这个数最小是 . 【考点】平方数特征之奇数个约数 【难度】4星 【题型】填空 【关键词】希望杯,六年级,二试,第9题,5分 【解析】 设为(为不含质因子2,3的整数),则它的是是立方数,所以是3的倍数,是3的倍数,另外它的即是一个平方数,所以是偶数,是奇数,符合以上两个条件的的最小值为4,的最小值为,这个数最小为432. 【答案】432 (1) 平方数的整除特性 【例 5】 三个连续正整数,中间一个是完全平方数,将这样的三个连续正整数的积称为“美妙数”。问所有的小于2008的“美妙数”的最大公约数是多少? 【考点】平方数特征之平方数的整除特性 【难度】2星 【题型】填空 【关键词】华杯赛,决赛,第11题,10分 【解析】 ①任何三个连续正整数,必有一个能为3整除.所以,任何“美妙数”必有因子3. ②若三个连续正整数中间的数是偶数,它又是完全平方数,必定能为4整除;若中间的数是奇数,则第一和第三个数是偶数,所以任何“美妙数”必有因子4. ③完全平方数的个位只能是1、4、5、6、9和0,若其个位是5和0,则中间的数必能被5整除,若其个位是1和6,则第一个数必能被5整除,若其个位是4和9,则第三个数必能被5整除.所以,任何“美妙数”必有因子5. ④上述说明“美妙数”都有因子3、4、和5,也就有因子60,即所有的美妙数的最大公约数至少是60.60=3×4×5是一个“美妙数”,美妙数的最大公约至多是60.所有的美妙数的最大公约数既不能大于60,又至少是60,只能是60。 【答案】 【例 1】 证明:形如11,111,1111,11111,…的数中没有完全平方数。 【考点】平方数特征之平方数的整除特性 【难度】2星 【题型】解答 【解析】 略 【答案】由于奇数的平方是奇数,偶数的平方为偶数,而奇数的平方除以4余1,偶数的平方能被4整除.现在这些数都是奇数,它们除以4的余数都是3,所以不可能为完全平方数. 【例 2】 记,这里.当k在1至100之间取正整数值时,有 个不同的k,使得S是一个正整数的平方. 【考点】平方数特征之平方数的整除特性 【难度】3星 【题型】填空 【关键词】少年数学智力冬令营 【解析】 一个平方数除以4的余数是0或1.当时,S除以4余3,所以S不是平方数;当时, ,当k在1至100之间时,S在13至409之间,其中只有8个平方数是奇数:,,,,,,,,其中每1个平方数对应1个k,所以答案为8. 【答案】8 【例 3】 能够找到这样的四个正整数,使得它们中任意两个数的积与的和都是完全平方数吗?若能够,请举出一例;若不能够,请说明理由. 【考点】平方数特征之平方数的整除特性 【难度】4星 【题型】解答 【解析】 略 【答案】因为偶数的平方能被4整除,奇数的平方被4除余1,因此任一正整数的平方被4除余0或1. 假设存在四个正整数,使得.又被4除余2,故被4除余2或3. 若中有两个偶数,如是偶数,那么是4的倍数,被4除余2,,所以不可能是完全平方数; 因此中至多只有一个偶数,至少有三个奇数.设为奇数,为偶数,那么被4除余1或3,所以中至少有两个数余数相同.如被4除余数相同,同为1或3,那么 被4除余1,所以被4除余3,不是完全平方数; 综上,不可能全是完全平方数. 【例 4】 的末三位数是多少? 【考点】平方数特征之平方数的整除特性 【难度】5星 【题型】解答 【解析】 首先,仅考虑后三位数字,所求的数目相当于的平方再乘以的末三位.而 , 其末三位为;然后来看前者.它是一个奇数的平方,设其为 (k为奇数),由于,而奇数的平方除以8余1,所以是8的倍数,则是200的倍数,设,则,所以它与105的乘积 ,所以不论m的值是多少,所求的末三位都是625. 【答案】625 【例 1】 求所有的质数P,使得与也是质数. 【考点】平方数特征之平方数的整除特性 【难度】5星 【题型】解答 【解析】 如果,则,都是质数,所以5符合题意.如果P不等于5,那么P除以5的余数为1、2、3或者4,除以5的余数即等于、、或者除以5的余数,即1、4、9或者16除以5的余数,只有1和4两种情况.如果除以5的余数为1,那么除以5的余数等于除以5的余数,为0,即此时被5整除,而大于5,所以此时不是质数;如果除以5的余数为4,同理可知不是质数,所以P不等于5,与至少有一个不是质数,所以只有满足条件. 【答案】5 【例 2】 古时候有两位贩卖家畜的商人把他们共有一群牛卖掉,每头牛买得的钱数正好等于牛的头数。他们把所得的钱买回了一群羊,每只羊10文钱,钱的零头又买了一只小羊。他们平分了这些羊,结果第一个人多得了一只大羊,第二人得到了那只小羊。为了公平,第一个人应补给第二个人____文钱。 【考点】平方数特征之平方数的整除特性 【难度】5星 【题型】填空 【关键词】走美杯,四年级,初赛,第15题 【解析】 根据题意,设每头牛的价钱为10a+b(a、b不同为0,a、b为自然数),因为题目中明显给出“每头牛卖的钱数正好等于牛的头数”可知买牛人所得到钱数为:,由题意得这个总数的十位数字必为奇数否则不会达到“平分这些羊,并且一个人得到一只大羊,第二个人得到了那只小羊”,而的十位必为偶数,所以只要看的值,尝试得到只有16和36满足条件,所以小羊的价格应该为6,那么第一个人应该补给第二个人:(文) 【答案】文钱查看更多