- 2022-02-11 发布 |
- 37.5 KB |
- 38页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
青岛版六年级上数学总复习专题1 数与代数
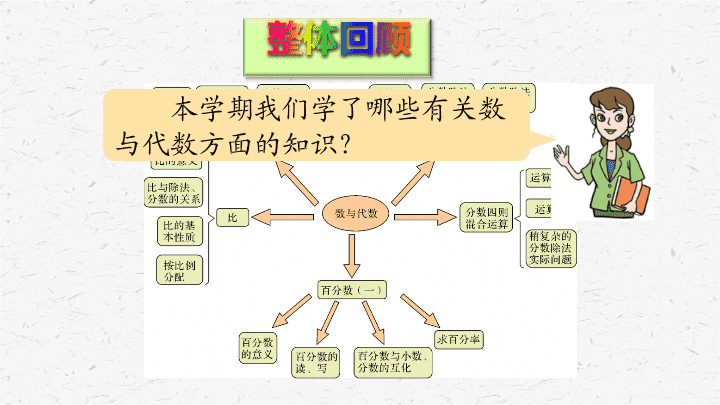
青岛版六年级上册 数与代数 —— 总复习 回顾整理 八 整体回顾 本学期我们学了哪些有关数与代数方面的知识? 我这样整理有关 分数乘除法 的知识。 转化 分数乘整数: 求几个相同加数的和的简便运算。 一个数乘分数: 求一个数的几分之几是多少。 1 1 分子相乘的积作分子,分母相乘的积作分母,结果要化成最简分数。 分数除以整数 : 等于分数乘以整数的倒数。 一个数除以分数: 等于这个数乘以分数的倒数。 2 1 2 1 甲数除以乙数( 0 除外),等于甲数乘乙数的倒数。 1. 六年级男生有 24 人,女生是男生的 ,女生有多少人? 分数乘法应用题:求一个数的几分之几是多少用乘法计算,即一个数 × 几分之几。 答:女生有 22 人。 2. 白兔有 32 只,是黑兔只数的 。黑兔有多少只? 分数除法应用题:已知一个数的几分之几是多少,求这个数。可设这个数为 x ,列方程解答: x × 几分之几 = 已知量。 解:设黑兔有 x 只。 答:黑兔有 72 只。 分数四则 混合运算 运算顺序 运算律 解决问题 分数四则混合运算 有哪些知识点? 运算顺序: 分数四则混合运算的运算顺序与整数四则混合运算的相同。 整数的运算律适用于分数。 运算律: 解决稍复杂的有关分数的实际问题: ( 1 )已知一个数以及另一个数比它多(或少)几分之几,求另一个数,用乘法计算。 ( 2 )已知一个数的几分之几是多少,求这个数,设这个数为 x ,列方程解答。 一辆摩托车每时可以行驶 60 千米,一辆自行车的速度比它的 多 3 千米。自行车每小时能行多少千米? 答:自行车每小时能行 18 千米。 修一条公路,分为两个工期,第一个工期修了 90 千米。第二个工期修的路长占这条公路的 。这条公路全长多少千米? 解:设这条公路全长 x 千米。 答:这条公路全长 150 千米。 对于 比 的知识你都了解了哪些? 各部分名称 意义、 比的基本性质 比、除法、分数三者关系 按比例分配 求比值 化简比 比 人体血液中,红细胞的平均寿命是120天,血小板的平均寿命是10天,写出红细胞与血小板的寿命比。 120 ∶ 10 赵凡3分钟走了330米,赵凡的行走路程与时间的比是多少? 330 ∶ 3 比的意义 : 两个数相除又叫做两个数的比。 比各部分的名称 : : : : : : : : 前 项 比 值 比 号 后 项 求比值 : 比的前项除以后项所得的商叫做比值。 比、分数和除法之间有什么关系和区别? 比 分数 除法 前项 :(比号) 后项 比值 分子 被除数 ÷ (除号) — (分数线) 分母 除数 分数值 商 比的后项可以是 0 吗? 比和分数都可以表示两个数量之间的关系。 除法是一种运算;分数是一种数;比只能表示两个数量之间的关系。 比的基本性质 : 比的前项和后项同时乘或除以同一个数( 0 除外),比值不变。 14∶ 2 1 = ( 14÷7 ) ∶ ( 2 1 ÷7 ) = 2 ∶3 按比分配: 在实际问题中,需要把一个量按照一定的比来进行分配。一般用分数乘法解答: 学校舞蹈队共有 40 人,其中男、女队员的人数比是 3∶7 。男、女队员各有多少人? 男生人数占舞蹈队总人数的 ,女生人数占舞蹈队总人数的 。 答:男队员有 12 人,女队员有 28 人。 对于百分数的知识你都了解了哪些? 百分数 百分数的意义 百分数与分数的联系 百分数与分数、小数的互化 用百分数解决问题 百分数的意义 : 表示一个数是另一个数的百分之几的数叫百分数。百分数也叫百分率或百分比。 在这里,98 %表示: 这瓶饮料中野山楂汁成分占果汁总成分的 。 百分数与分数的联系: 意 义 单位名称 百分数 分 数 百分数不能带单位名称。 表示两个数之间的关系。 分数既可以表示一个具体的数量,又可以表示两个数之间的关系。 分数在表示具体数量时可以带单位名称。 小数 分数 百分数 0.75 0.75= =75% 75 100 75% 3 4 75%= =0.75 75 100 0.75= = 75 100 3 4 =3 4=0.75 3 4 ÷ 75%= = 75 100 3 4 =3 4=0.75=75% 75 100 ÷ 小数点向右移动两位 , 添上 % 去掉%,小数点向左移动两位 先化成小数 , 再化成百分数 先写成分数 , 再约分 先用分数表示 , 再约分 分子除以分母 百分数与分数、小数的互化 解决问题 : 求一个数是另一个数的百分之几,用一个数 ÷ 另一个数 ( 单位“ 1 ” ) ,结果用百分数表示。 六年级一班有 40 人,其中男生 22 人。男生占 全班人数的 百分之几? 答:男生占全班人数的 55 %。 2 2 ÷ 40 = 0. 55 = 55 % 自主练习 1. 解方程。 2. 生态游乐园的票价比去年提高了 。去年成人和儿童的票价各是多少元? 解:设去年成人票价是 m 元。 解:设去年成人票价是 n 元。 3. 某制药厂要配制一种注射液,药物浓缩液与蒸馏水的比是 1∶19 。如果配制 5000 升这样的注射液,需要浓缩液和蒸馏水各多少升? 答: 需要浓缩液 250 升 ,蒸馏水 4750 升。 4. 北京到青岛的铁路长约 900 千米,一列火车 4 小时行驶了全程的 。照这样计算,从北京到青岛大约需要几小时? 答:从北京到青岛大约需要 12 小时。 5. 某校师生人数及占地面积变化情况如下。 ( 1 )建校初期有 15 位教师,相当于现在的 。现在有多少位教师? 解:设现在教师有 x 人。 答:现在教师有 60 人。 5. 某校师生人数及占地面积变化情况如下。 ( 2 )现在学生有 1600 人,与建校初期学生人数的比是 16∶3 。建校初期学生有多少人? 1600÷16×3 = 100×3 = 300 (人) 答:建校初期学生有 300 人。 5. 某校师生人数及占地面积变化情况如下。 ( 3 )建校初期占地面积是 2500 平方米,比现在少 。现在学校占地面积是多少平方米? 解:设现在学校占地面积是 x 平方米。 答:现在学校占地面积是 3000 平方米。 6. 一本故事书有 150 页,小亮第一天看了全书的 。 ( 1 )如果第二天看的相当于第一天的 ,第二天看了多少页? 答:第二天看了 24 页。 6. 一本故事书有 150 页,小亮第一天看了全书的 。 ( 2 )如果第一天与第二天看的页数的比是 5∶4 ,第二天看了多少页? 答:第二天看了 24 页。 6. 一本故事书有 150 页,小亮第一天看了全书的 。 ( 3 )如果第二天看了全书的 ,第二天比第一天多看多少页? 答:第二天比第一天多看了 10 页。查看更多