总复习12 图形的认识与测量

总复习12 图形的认识与测量

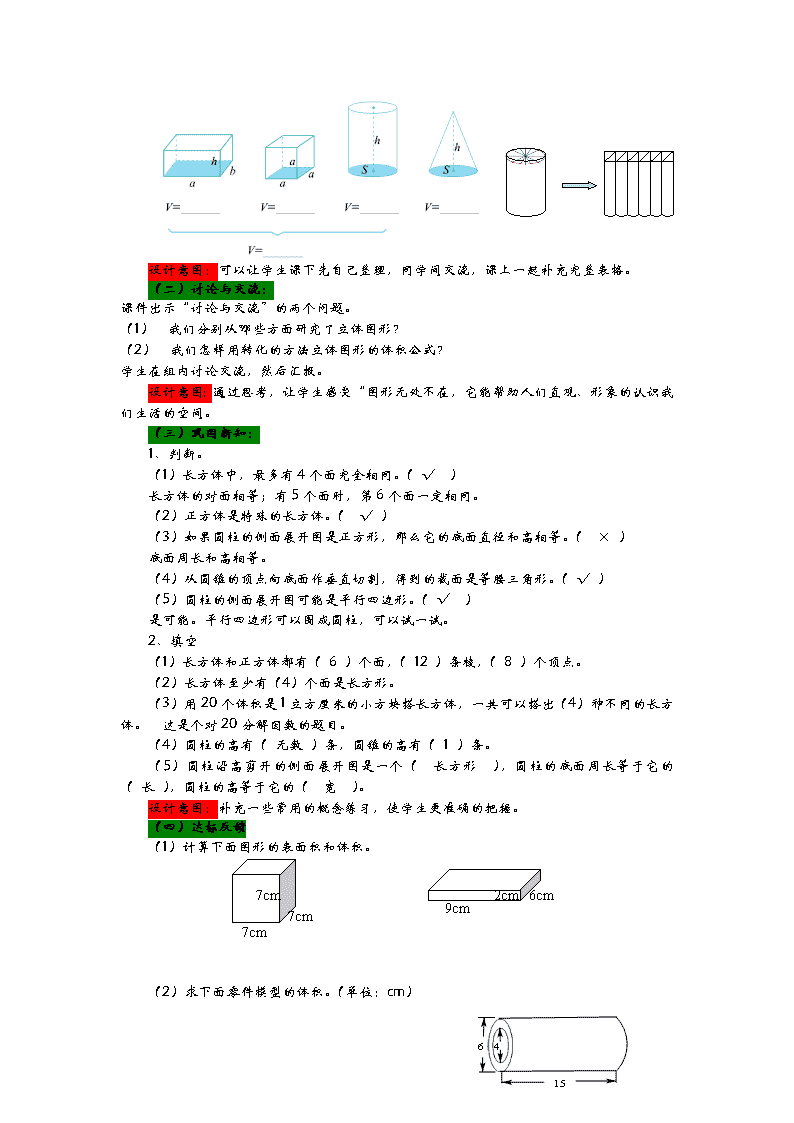
‎12 图形的认识与测量 n 教学内容 教材第102～103页，图形的认识与测量 n 教学提示 ‎ 如何把实际问题抽象成数学问题。‎ n 教学目标 知识与能力 掌握所学几何形体的特征；能够比较熟练的计算一些几何形体的周长、面积和体积，并能应用；巩固所学的简单的画图、测量等技能。‎ 过程与方法 进一步感受几何知识之间的相互联系，体会几何学习的作用，能够比较灵活的运用所学知识解决生活中一些简单的实际问题。‎ 情感、态度与价值观 感受数学的应用价值，能在数学学习活动中获得成功体验，提升数学素养。‎ n 重点、难点 重点：掌握所学几何形体的特征；能够熟练的进行相关计算，能够比较灵活的运用所学知识解决生活中一些简单的实际问题。‎ 难点：能够比较灵活的运用所学知识解决生活中一些简单的实际问题。‎ n 教学准备 教师准备：几何模型；实物投影仪；多媒体课件。‎ n 教学过程 ‎（一）复习导入：‎ ‎1、怎样整理立体图形的有关知识？请同学们以小组为单位，合作分类整理，然后交流汇报。‎ 通过学生相互补充，逐步完善。‎ 名称 特征 棱长之和、体积公式 正方体 长 方体 圆柱 圆锥 ‎2、我们学过的立体图形的体积公式是怎样推导出来的？它们之间有怎样的联系？‎ 首先回忆什么是体积？怎样规定的体积单位？‎ 物体所占空间的大小叫体积。长是1厘米的正方体的体积叫1立方厘米。‎ 然后用边长1厘米的正方体拼长方体，归纳总结规律：长方体的面积等于长、宽、高的乘积。即：长方体的体积=长×宽×高。（这是一个经验公式）‎ 其他公式都借助了转化的思想方法。‎ 设计意图：可以让学生课下先自己整理，同学间交流，课上一起补充完整表格。‎ ‎（二）讨论与交流：‎ 课件出示“讨论与交流”的两个问题。‎ （1） 我们分别从哪些方面研究了立体图形？‎ ‎（2） 我们怎样用转化的方法立体图形的体积公式？‎ 学生在组内讨论交流，然后汇报。‎ 设计意图：通过思考，让学生感受“图形无处不在，它能帮助人们直观、形象的认识我们生活的空间。‎ ‎（三）巩固新知：‎ ‎1、判断。‎ ‎（1）长方体中，最多有4个面完全相同。（ √ ）‎ 长方体的对面相等；有5个面时，第6个面一定相同。‎ ‎（2）正方体是特殊的长方体。（ √ ）‎ ‎（3）如果圆柱的侧面展开图是正方形，那么它的底面直径和高相等。（ × ）‎ 底面周长和高相等。‎ ‎（4）从圆锥的顶点向底面作垂直切割，得到的截面是等腰三角形。（ √ ）‎ ‎（5）圆柱的侧面展开图可能是平行四边形。（ √ ）‎ 是可能。平行四边形可以围成圆柱，可以试一试。‎ ‎2、填空 ‎（1）长方体和正方体都有（ 6 ）个面，（ 12 ）条棱，（ 8 ）个顶点。‎ ‎（2）长方体至少有（4）个面是长方形。‎ ‎（3）用20个体积是1立方厘米的小方块搭长方体，一共可以搭出（4）种不同的长方体。 这是个对20分解因数的题目。‎ ‎（4）圆柱的高有（ 无数 ）条，圆锥的高有（ 1 ）条。‎ ‎（5）圆柱沿高剪开的侧面展开图是一个（ 长方形 ），圆柱的底面周长等于它的（ 长 ），圆柱的高等于它的（ 宽 ）。‎ 设计意图：补充一些常用的概念练习，使学生更准确的把握。‎ ‎（四）达标反馈 ‎（1）计算下面图形的表面积和体积。‎ ‎7cm ‎7cm ‎7cm ‎9cm ‎2cm ‎6cm ‎（2）求下面零件模型的体积。（单位：cm）‎ ‎（3）一块三角形的地，底为125米，高为60米，一共收小麦22500千克。平均每公顷的产量是多少千克？合多少吨？‎ ‎（4）一个长方形的长减少8厘米，宽减少4厘米，原长方形的面积就减少92平方厘米，剩下的是一个正方形。这个正方形的面积是多少平方厘米？‎ ‎（5）一个没有盖子的圆柱形铁皮水桶，高7分米，底面周长是12.56分米，做这个水桶大约用铁皮多少平方分米？（得数保留整数）‎ ‎（6）一个长方体鱼塘，长20米，宽15米，深4米。如果1立方米的水重1吨，这个鱼塘能容纳多少吨水？‎ ‎（7）将9.42升水倒入一个底周长是62.8厘米的圆柱形水桶中，水深多少厘米？‎ ‎（8）一个长方体的棱长总和为48厘米，它的长、宽、高的比为3:2:1，这个长方体的体积是多少立方厘米？‎ ‎（9）一个圆锥形沙堆，占地面积为15平方米，高2米。把这队沙铺在宽8米的路面上，平均铺厚5厘米，能铺路多少米？‎ 答案：（1）294平方厘米，343立方厘米；168立方厘米，108立方厘米；（2）235.5立方厘米；（3）60000千克，60吨；（4）25平方厘米；（5）101平方分米；（6）1200吨；（7）30厘米；（8）48立方厘米；（9）25米。‎ 设计意图：检验当堂学习的效果。‎ ‎（五）课堂小结 这节课你学会了什么，有哪些收获？给大家说说。‎ 谁能把我们今天的问题再叙述一下？思路是怎样的？你理解了吗？‎ 设计意图：通过总结，既能够使学生加深对所学内容本质的理解和深层次思考，从而将 所学知识纳入自己的认知结构，又提升了学生的梳理和概括能力。‎ ‎（六）布置作业 第2课时：图形的认识与测量 ‎1、填空。‎ ‎（1）把三个棱长都是4厘米的正方体拼成一个长方体，这个长方体的棱长之和是（ ）厘米，表面积减少了（ ）平方厘米。‎ ‎（2）如右图，把一个地面直径为5分米的圆柱转化成 ‎ 一个与它等底等高的近似的长方体，这个长方体和圆 柱体的（ ）、（ ）、（ ）相等；表面积增 加了50平方分米，这个圆柱的体积是（ ）立方分米。‎ ‎（3）一个圆柱的侧面积是62.8平方厘米，高是5厘米，底面周长是（ ）厘米，体积是（ ）立方厘米。‎ ‎2．选择。‎ ‎(1) 做一个底面直径2分米，高10分米的圆柱形铁皮通风管（接头处不计），至少要（ ）平方分米铁皮。‎ A. 65.94 B. 62.8 C. 69.08 D. 31.4‎ ‎(2) 把一个圆柱体等分16份后，拼成一个近似的长方 体（如图），它们的（ ）相等，（ ）不相等。‎ A. 体积 B. 表面积 ‎(3) 圆柱内的沙子占圆柱的，倒入（ ）内正好倒满。‎ ‎ A B C ‎(4) 一个棱长为2厘米的正方体，如图挖掉一个 棱长为1厘米的小正方体后，它的表面积（ ）‎ A. 比原来大 B. 比原来小 ‎20‎ ‎15‎ 单位：厘米 C. 不变 D. 不能确定 ‎3. 用彩带捆扎一个圆柱形的蛋糕盒（如图），打结处 正好是底面圆心，打结用去彩带25厘米。‎ ⑴扎这个蛋糕盒至少用去多少厘米彩带？‎ ⑵在它的整个侧面贴上商标，商标的面积为多少平方厘米？（接头处忽略不计）‎ ⑶蛋糕盒的体积约是多少立方厘米？（保留一位小数）‎ 答案：1、（1）80，64；（2）底面积，高，体积，196.25；（3）12.56，62.8；2、(1) B（2）A，B（3）A(4)；3、（1）165厘米（2）942平方厘米（3）4710立方厘米。‎ 板书设计 图形的认识与测量 名称 特征 棱长之和、体积公式 正方体 长 方体 圆柱 圆锥 n 教学资料包 教学资源 把一个高是3分米的圆柱形底面分成许多个相同的小扇形，然后把这个圆柱沿着小扇形纵向切开，拼成一个与它等底等高的近似长方体。这个长方体的表面积比圆柱增加了36平方分米，求圆柱的体积。‎ 答案：339.12立方分米。‎ 资料链接 祖冲之 ‎ （429～500） 南北朝时期杰出的数学家和天文学家。字文远。祖籍范阳逎县（今河北涞水），先世迁居江南。父祖皆谙熟天算，学识渊博，为时人所敬重。冲之少传家业，青年时代入华林学省，从事学术研究。此后，历仕刘宋、南齐，官至长水校尉。他在数学、天文历法、机械制造等方面都有重大成就。‎ 在数学方面，祖冲之推算出圆周率π的不足近似值（朒数）3.1415926和过剩近似值（盈数）3.1415927，指出π的真值在盈、朒两限之间，即3.1415926＜π＜3.1415927，并用以校算新莽嘉量斛的容积。这个圆周率值是当时世界上最先进的数学成就，直到15世纪阿拉伯数学家阿尔·卡西（al-kāshī）和16世纪法国数学家韦达（1540～1603）才得到更精确的结果。祖冲之还确定了两个分数形式的圆周率值，约率π=22/7（≈3.14），密率π=355/113（≈3.1415929），其中密率是在分母小于1000条件下圆周率的最佳近似分数。密率为祖冲之首创，直到16世纪才被德国数学家奥托（1550～1605）和荷兰工程师安托尼兹（1543～1620）重新得到。在西方数学史上，这个圆周率值常被称为安托尼兹率。祖冲之和其子祖暅，在刘徽工作的基础上圆满解决了球体积计算问题。他们得到下列结果：“牟合方盖”（底径相等的两圆柱直交之公共部分）的体积等 ‎ 推算过程中提出了“幂势既同，则积不容异（二立体等高处截面积恒相等，则二立体体积相等）”原理。这个原理，直到17世纪才为意大利数学家卡瓦列利（1598～1647）重新提出，而被称为卡瓦列利原理，中国现在一般称为祖暅公理。据《隋书·律历志》记载，祖冲之对于二次方程和三次方程也有所研究。所著《缀术》一书，是著名的《算经十书》之一，曾被唐代国子监和朝鲜、日本用做算学课本，惜已失传。‎ ‎ 在天文历法方面，祖冲之在长期观测、精确计算和对历史文献深入研究的基础上，创制了《大明历》。他最早把岁差引进历法，提高历法精确性，这是中国历法史上的重大进步。他还采用了391年有144个闰月的新闰周，突破了沿袭很久的19年7闰的传统方法。《大明历》中使用的数据，大多依据长期实测的结果，相当精确。按照祖冲之的数据计算，一个回归年的日数为365.24281481平太阳日。一个交点月的日数为27.21223平太阳日，关于木星（当时称岁星）每84年超辰一次的结论，相当于求出木星公转周期为11.858年。这些都非常接近现测数值。所推算的五大行星会合周期，也是当时最好的结果。他还发明用圭表测量冬至前后若干天的正午太阳影长以定冬至时刻的方法。这个方法也为后世长期采用。宋孝武帝大明六年（462），祖冲之上书刘 宋朝廷，请求颁行《大明历》，但遭到皇帝宠臣戴法兴的反对。戴法兴指责引进岁差和改革闰周等违背了儒家经典，是“诬天背经”。祖冲之据理力争，针锋相对地写了一篇辩驳的奏章。他表示“愿闻显据，以核理实”，并引用历史文献和天象观测的大量事实，逐条批驳了戴法兴的论点。他明确指出天体运行“有形可检，有数可推”，是有规律的。科学在不断进步，人们不能“信古而疑今”，充分体现了一位科学家坚持真理，革旧创新的可贵精神。但是，祖冲之生前《大明历》未能颁行。后经祖暅三次上书朝廷，推荐《大明历》，终于在梁武帝天监九年（510）被采用颁行，前后行用八十年，对后世历家产生了重要的影响。‎ ‎ 祖冲之是一位博学多才的科学家和发明家。对于机械原理也很有研究。他曾设计制造水碓磨（利用水力加工粮食的工具）、铜制机件传动的指南车、一天能走百里的“千里船”和“木牛流马”等水陆运输工具。还设计制造过漏壶（古代计时器）和巧妙的欹器，并精通音律。他的著述很多，《隋书·经籍志》著录有《长水校尉祖冲之集》五十一卷，散见于各种史籍记载的有《缀术》、《九章算术注》、《大明历》、《驳戴法兴奏章》、《安边论》、《述异记》、《易老庄义》、《论语孝经释》等。其中大部分已失传，现在仅能见到《上大明历表》、《大明历》、《驳戴法兴奏章》、《开立圆术》等有限的几篇。其子祖暅、孙祖皓也都是南朝有名的天文学家和数学家。‎ ‎ 为了纪念和表彰祖冲之在科学上的卓越贡献，人们建议把密率355/113称为“祖率”，紫金山天文台已把该台发现的一颗小行星命名为“祖冲之”，在月球背面也已有了以祖冲之名字命名的环形山。‎