六年级数学下册课件-5 数学广角—鸽巢问题 -人教版 (2)

六年级数学下册课件-5 数学广角—鸽巢问题 -人教版 (2)

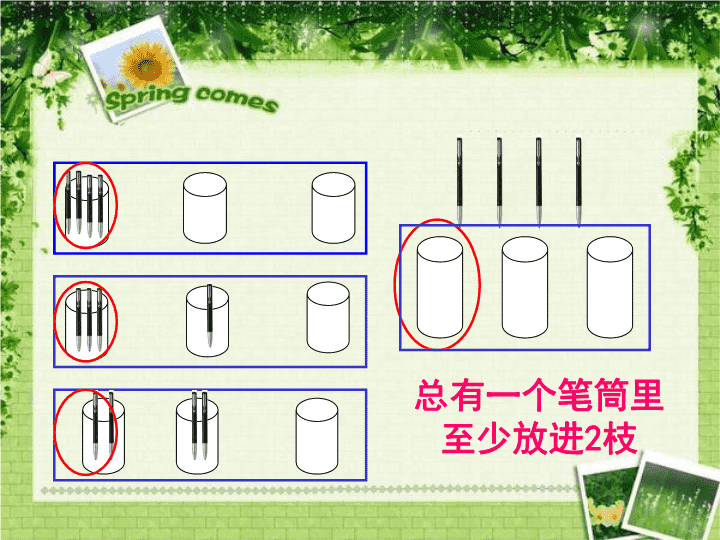
把4枝笔放进3个笔筒里，可以怎么 放？有几种情况？ 总有一个笔筒里 至少放进2枝 为什么不管怎么放，总有一个笔筒里至 少放进2枝笔?同桌之间相互交流一下。 有一个笔筒里至少放进2枝 如果我们先把4支笔平均分到3个笔筒， 让每个笔筒里先放1枝笔，最多放3枝。 剩下的1枝还要放进其中的一个笔筒。 所以不管怎么放，总有一个笔筒里至少 放进2枝笔。 为什么先要平均分呢？ 只有平均分才能将笔尽可能的分散，保 证“至少”的情况。 把5本书进2个抽屉中，不管怎么放， 总有一个抽屉至少放进3本书。 这是为什么？ 5÷2=2……1 把7本书进2个抽屉中，不管怎么放，总有一个 抽屉至少放进多少本书？为什么？ 7÷2=3……1 把9本书进2个抽屉中，不管怎么放， 总有一个抽屉至少放进多少本书？为什么？ 9÷2=4……1 8÷3=2……2 8只鸽子飞回3个鸽舍，至少有（ ）只 鸽子要飞进同一个鸽舍。为什么？ 3 我们先让一个鸽舍里飞进2只鸽子，3个鸽舍最多可飞进 6只鸽子，还剩下2只鸽子，无论怎么飞，所以至少有3只 鸽子要飞进同一个笼子里。 至少数=计算绝招: 把5本书进2个抽屉中，不管怎么放，总有一个抽屉 至少放进3本书 5÷2=2……1 把7本书进2个抽屉中，不管怎么放，总有一个抽屉 至少放进4本书 7÷2=3……1 把9本书进2个抽屉中，不管怎么放，总有一个抽屉 至少放进5本书 9÷2=4……1 8只鸽子飞回3个鸽舍，至少有3只鸽子要飞进同一个 鸽舍 8÷3=2……2 商数+1 • 抽屉原理： 把m个物体任意分放进n个空抽屉里 (m>n) ，如果m n=a…b 那么一定 有一个抽屉中放进了至少 个 物体。  a+1 “抽屉原理”最先是由19世纪的德 国数学家狄里克雷（Dirichlet）运用于解 决数学问题的，所以又称“狄里克雷原 理”，也称为“鸽巢原理”。“抽屉原理” 的应用却是千变万化的，用它可以解决许 多有趣的问题，并且常常能得到一些令人 惊异的结果。“抽屉原理”在数论、集合 论、组合论中都得到了广泛的应用。 狄里克雷 （1805～1859） 抽屉原理简介 一盒围棋棋子，黑白子混放，我们任意摸出 3个棋子，至少有2个棋子是同颜色的. 想一想 在我们班的任意13人中，总有至少 几个人的属相相同，为什么？ 六（1）班有38位同学，至少有 （ ）人是同一个月过生日的。 38÷12=3……2 3+1=4（人） 4 四种花色 抽 牌 一副扑克牌(除去大小王)52张中有四 种花色，从中随意抽5张牌，无论怎么 抽,为什么总有两张牌是同一花色的？ 温馨提示 在有些问题中，“抽屉”和“物体”不是很明 显， 需要我们制造出“抽屉”和“物体”。 制造出“抽屉”和“物体”是比较困难的，这一方 面需要同学们去分析题目中的条件和问题，另一方 面需要多做一些题来积累经验。 …… • 作业： 课本P • 思考题： 任意写出3个自然数，其中必定有2个自然数的和 是2的倍数。你认为这句话对吗？为什么？