五年级上册数学课件-第六单元第3课时 梯形的面积 人教版(共22张PPT)

五年级上册数学课件-第六单元第3课时 梯形的面积 人教版(共22张PPT)

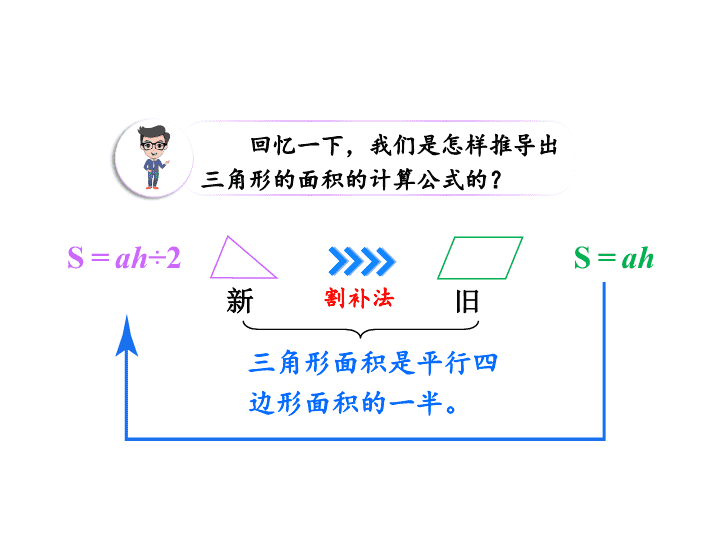
多边形的面积 6 人教版五年级数学上册 第 3 课时 梯形的面积 一 情境导入 车窗玻璃的形状是梯形，怎样求出它的面积呢？ 根据学过的推导方法推出梯形的面积公式吧。 回忆一下，我们是怎样推导出三角形的面积的计算公式的？ 割补法 三角形面积是平行四边形面积的一半。 S = ah S = ah ÷2 旧 新 根据这样的思路，我们来推导一下梯形面积的计算公式。 割补法 三角形面积是平行四边形面积的一半。 S = ah S = ah ÷2 旧 新 二 新课探究 ( 教科书第 95 页 ) 请根据已有的知识经验，借助课前准备的学具推导出梯形的面积计算公式。（ 在使用剪刀时，一定要注意安全。 ） （ ） 拼接法 平行四边形面 积 底 高 × = 相等 相等 相等 2 个完全一样的梯形面积 上底下底的和 高 × = 梯形的面积 上底 高 × = ÷ 2 上底 下底 高 + 下底 上底 下底 + 底边 下底 上底 梯形的面积 = 平行四边形面 积 + 三角形面 积 上底 分割法 1 分割 法 1 梯形的面积 = 平行四边形面 积 + 三角形面 积 上底 上底 下 底 − 上 底 高 高 S 平行四边 形 = ah = 上底 × 高 梯形的面积 = 平行四边形面 积 + 三角形面 积 上底 上底 下 底 − 上 底 高 高 S 三角 形 = ah ÷ 2 = （下 底 − 上底） × 高 ÷ 2 分割 法 1 梯形的面积 = 平行四边形面 积 + 三角形面 积 上底 × 高 + （下 底 − 上底 ) × 高 ÷ 2 = [ 上 底 + ( 下 底 − 上底 ) ÷ 2] × 高 = （上 底 ÷ 2 + 下 底 ÷ 2 ） × 高 = （上 底 + 下 底 ) × 高 ÷ 2 梯形的面积 = A 三角形面 积 + B 三角形面 积 下底 上底 A 三角形 B 三角形 上底 下底 高 高 分割法 2 A 三角形 B 三角形 上底 下底 高 高 S A 三角 形 = ah ÷ 2 = 上底 × 高 ÷ 2 梯形的面积 = A 三角形面 积 + B 三角形面 积 分割法 2 梯形的面积 = A 三角形面 积 + B 三角形面 积 A 三角形 B 三角形 上底 下底 高 高 S B 三角 形 = ah ÷ 2 = 下底 × 高 ÷ 2 = 上底 × 高 ÷ 2 + 下底 × 高 ÷ 2 = （上 底 + 下 底 ) × 高 ÷ 2 分割法 2 观察拼成的平行四边形和原来的梯形，你发现了什么？ 只要是两个完全一样的梯形，我们就能把 它们拼成一个平行四边形，平行四边形的底边等于梯形的上底加下底 。 观察原来的梯形和转化后的平行四边形，你发现它们之间有哪些等量关系？ 梯形的面 积 = （上 底 + 下 底 ) × 高 ÷ 2 如果用 S 表示 梯形的面积 ，用 a 表示梯形的 上底 ，用 b 表示梯形的 下底 ，用 h 表示梯形的 高 ，梯形的面积计算公式可以写成： S= ( a+b ) h ÷2 。 a h b 应用梯形的面积解决问题 我国三峡水电站大坝的横截面的一部分是梯形（如下图 ), 求它的面积。 3 ( 教科书第 96 页例 3) S =( a+b ) h ÷ 2 =( 3 6+ 12 0) × 135 ÷ 2 = 1053 0( m 2 ) 答 ： 它的面积 是 1053 0 m 2 。 = 156 × 135 ÷ 2 三 随堂练习 S 1 = ( a 1 + b 1 ) h ÷ 2 = ( 40 + 71 ) × 40 ÷ 2 = 222 0( c m 2 ) = 111 × 40 ÷ 2 ( 教科书第 96 页做一做 ) 一辆汽车侧面的两块玻璃的形状是梯形（如下图），它们的面积分别是多少？ ① ② 三 随堂练习 一辆汽车侧面的两块玻璃的形状是梯形（如下图），它们的面积分别是多少？ 答：它们的面积分别是 222 0 cm ² 、 220 0 cm ² 。 ① ② S 2 = ( a 2 + b 2 ) h ÷ 2 = ( 4 5+ 6 5) × 40 ÷ 2 = 220 0( c m 2 ) = 110 × 40 ÷ 2 ( 教科书第 96 页做一做 ) 四 培优训练 在下图中，梯形的下底 是 17. 5 cm, 高 是 5 cm ，两个底角都 是 45° ，求梯形的面积。 答：梯形的面积 是 62. 5 cm 2 。 梯形的上底是： 17. 5− 2× 5= 7. 5( c m ) 17.5 5 45° 45° 5 5 5 梯形的面积是： ( 7. 5+ 1 7.5 )×5 ÷ 2 = 62. 5( cm 2 ) 五 课堂小结 梯形的面 积 = （上底 + 下底） × 高 ÷2 S= ( a +b ) h ÷ 2 课后作业 1. 从课后习题中选取； 2. 完成练习册本课时的习题。