人教版二年级上册 期末复习 知识点总结

人教版二年级上册 期末复习 知识点总结

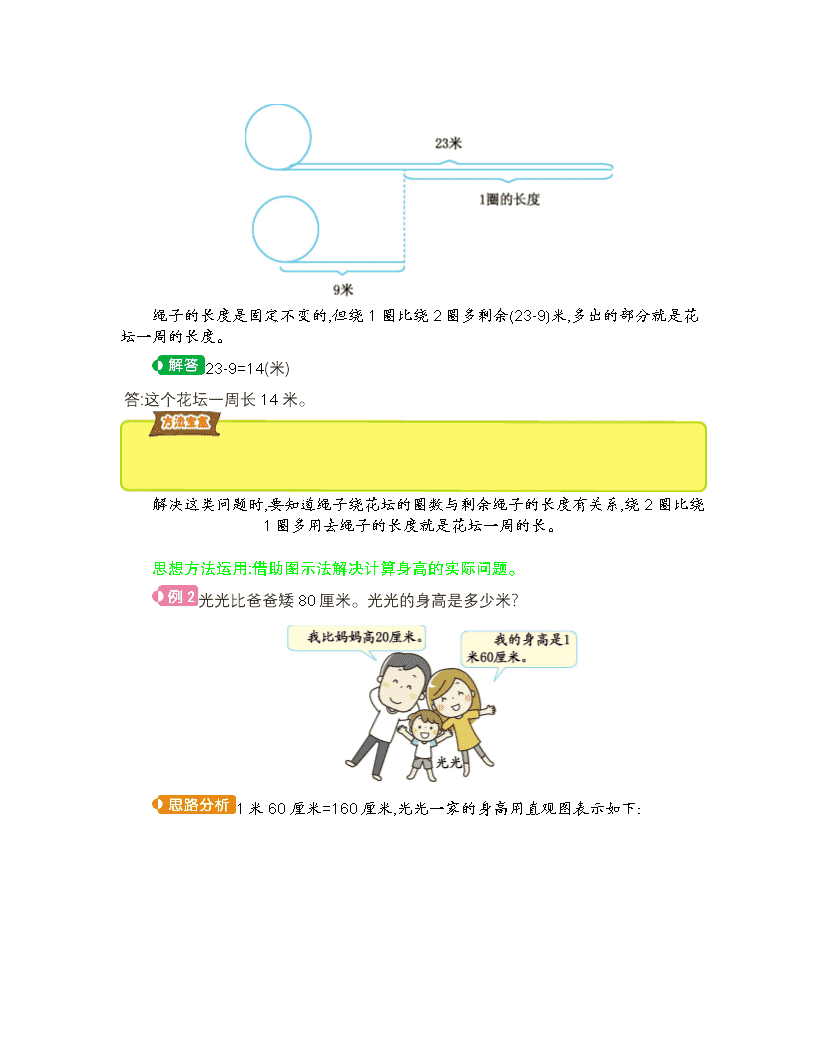
第一单元总结 思想方法运用:运用推理法解决测量问题。‎ 方方用一根绳子测量一个花坛一周的长度,他把绳子绕花坛1圈后,绳子剩下23米,绕花坛2圈后,绳子剩下9米。这个花坛一周长多少米?‎ 题中两次的测量情况可用下图表示出来:‎ 绳子的长度是固定不变的,但绕1圈比绕2圈多剩余(23-9)米,多出的部分就是花坛一周的长度。‎ ‎23-9=14(米)‎ ‎ 答:这个花坛一周长14米。‎ ‎　　解决这类问题时,要知道绳子绕花坛的圈数与剩余绳子的长度有关系,绕2圈比绕1圈多用去绳子的长度就是花坛一周的长。‎ 思想方法运用:借助图示法解决计算身高的实际问题。‎ 光光比爸爸矮80厘米。光光的身高是多少米?‎ ‎1米60厘米=160厘米,光光一家的身高用直观图表示如下:‎ ‎　　从图中可以看出,要求光光的身高是多少厘米,需要先求出爸爸的身高,即求比160多20的数是多少,列式是160+20=180;再求光光的身高是多少厘米,即求比180少80的数是多少,列式是180-80=100(厘米),最后再把100厘米换算成1米。‎ ‎1米60厘米=160厘米 ‎160+20-80=100(厘米)‎ ‎100厘米=1米 答:光光的身高是1米。‎ ‎　　本题中求出爸爸的身高是解决问题的关键,解决稍复杂的问题时,可以用直观图表示出题目中的数量关系,从而找到解决问题的方法。‎ 第二单元总结 思想方法运用:运用“移多补少”法解决实际问题。‎ 交换哪两筐,可以使两车运的苹果个数同样多?用箭头画一画,算一算。‎ 先分别求出每辆车上苹果的总个数,第1辆车上有26+30+28=84(个);第2辆车上有24+22+26=72(个);再算第1辆车上的苹果个数比第2辆车上多多少个,即84-72=12(个),12个的一半是6个,也就是从第1辆车上拿6个苹果给第2辆车,两车的苹果个数同样多;要求交换哪两筐,可以使两车运的苹果个数同样多,就找第1辆车上的哪筐苹果比第2辆车上的哪筐苹果多6个,观察发现:30-24=6(个),28-22=6(个),即有两种交换方法:‎ ‎　　30个　⇌　24个　　28个　⇌　22个 ‎　 第1辆车　 第2辆车　第1辆车　　第2辆车 口答:交换30个一筐的的和24个一筐的的这两筐或交换28个一筐的的和22个一筐的的,可以使两车运的苹果个数同样多。‎ ‎　　解决这类“移多补少”的问题时,可以从不同的角度思考。解题的键是掌握下面的数量关系:物体的总个数不发生变化,先求出总个数相差多少,再把多出的部分平均分成两半,把其中的一半给少的那个量。在此基础上,根据题意解答问题即可。‎ 思想方法运用:运用倒推法解决“将错就错”的问题。‎ 在计算一个数减去18时,马大哈将被减数的十位和个位上的数字互换了,结果得47。正确的差是多少?‎ ‎1.根据得到的差47和减数18,求出百位和十位互换后的被减数,即:18+47=65。‎ ‎2.由“65”可以推算出正确的被减数是“56”。‎ ‎3.求出正确的差:56-18=38。‎ ‎18+47=65　56-18=38‎ ‎　　解决这类问题时,可以“将错就错”先求出错误的被减数,然后根据错误的被减数推算出正确的被减数,进而计算出正确的结果 第三单元总结 思想方法运用:运用比较法解决问题。‎ 下面的两个角哪个大?你发现了什么?‎ 先制作两个长短不同的活动角,分别与图中的两个角一样大。借助活动角比一比,顶点对顶点,一边对一边,再看另一边。通过比较 可知,两个角一样大,由此可知,角的大小与边的长短无关,与两条边叉开的大小有关。‎ 两个角一样大。‎ 发现:角的大小与边的长短无关,只与两条边叉开的大小有关。叉开的越大,角就越大。叉开的越小,角就越小。‎ ‎　　角的大小与边的长短无关,只与角的两条边叉开的大小有关。‎ 第四单元总结 思想方法运用:运用求异思维解决实际问题。‎ 一张长方形餐桌配4把椅子,一张圆形餐桌配6把椅子。某宾馆大厅里摆了3张长方形的餐桌和5张圆形的餐桌,一共需要配多少把椅子?‎ 思路一:由题意可知,一张长方形餐桌配4把椅子,一张圆形餐桌配6把椅子。求3张长方形的餐桌和5张圆形的餐桌一共需要配多少把椅子,可以先分别求出3张长方形的餐桌和5张圆形的餐桌各需要配多少把椅子,再把需要的椅子数相加。‎ 思路二:可以把3张长方形的餐桌和5张圆形的餐桌即8张餐桌都配成4把椅子,列式是8×4,因为5张圆形的餐桌每张要配6把椅子,这样少算了5个2把,要加上。‎ 思路三:把每张餐桌都配成6把椅子,这样3张长方形的餐桌每张都多配了2把椅子,即多配了3个2把,要减去。‎ 方法一:3×4=12(把)　5×6=30(把)　12+30=42(把)‎ 方法二:5+3=8(张)　8×4=32(把)　5×2=10(把)　32+10=42(把)‎ 方法三:5+3=8(张)　8×6=48(把)　3×2=6(把)　48-6=42(把)‎ 口答:一共需要配42把椅子。‎ ‎　　解决实际问题时,要学会从不同的角度思考,灵活运用不同的方法解答。方法不唯一时,要选用简便的方法解答。‎ 第五单元总结 思想方法运用:运用观察分析法找不同。‎ 下面左图是一个正方体积木的展开图,如果把它折叠起来,就成了一个正方体。下面右边的五个正方体积木中,哪一个与它完全相同的?‎ 先把左边的图形折叠起来。可以发现折叠成的正方体中,与是两个相对的面;与是两个相对的面;与是两个相对的面。了解了每两个面之间的关系,再分别观察右面的五个正方体积木,①中,与是相邻的两个面,不是相对的 两个面,所以不选①;②和③中与是相邻的,不是相对的,所以也不选②和③;④中与是相邻的,而不是相对,所以也不同;只有⑤与原正方体积木完全相同。‎ ‎⑤‎ ‎　　根据看到的立体图形的形状来辨认它的摆放方式时,首先要了解这个物体相邻面以及相对的面分别是什么,然后根据确定的方位看到的形状来想象物体的摆放方式。‎ 第六单元总结 思想方法运用:运用图示法解决实际问题。‎ 一盒饼干,小冰第一次吃掉了一半,第二次又吃掉了剩下的一半,这时还剩下8块。这些饼干共有多少块?‎ 可以画图帮助理解题意:‎ 从图中可以看出,这盒饼干共有4个8块。‎ ‎8×4=32(块)‎ 口答:这些饼干共有32块。‎ ‎　　有些题很难找出题目中的数量关系,可以先动手折一折,画一画,再来解答比较容易。‎ 第七单元总结 思想方法运用:运用推理法解决时针与分针追赶问题。‎ ‎(1)(2)‎ 第一个钟面上,时针指着11,分针指着12,此时的时刻是11时,要知道再过多长时间分针能赶上时针,根据钟面上时针与分针的运动情况可知,12时时针与分针重叠在一起,从11时到12时经过了1小时,所以再过1小时分针能赶上时针。第二个钟面上,时针指着1,分针指着12,此时的时刻是1时,‎ 根据钟面上时针与分针的运动情况可知,3时整时,时针指着3,分针指着12,此时分针和时针形成的角是直角;9时整时,时针指着9,分针指着12,此时分针和时针形成的角是直角。‎ ‎(1)再过1小时分针能赶上时针。‎ ‎(2)(答案不唯一)9时整或3时整,分针和时针形成的角是直角。‎ ‎　　解决这类问题时,需要根据钟面上时针和分针的运动情况,通过想象得出答案。‎ 第八单元总结 思想方法运用:运用有序思维法解决搭配问题。‎ 幼儿园为女同学做演出服,上衣有红色、蓝色和黄色,裙子有黑色、白色、灰色和绿色。这些服装一共可以搭配出多少套不同的衣服?‎ 按照一定的顺序思考,如果穿红色上衣,就会有四种颜色的裙子可以搭配;同理,如果是穿黄色、蓝色的上衣,也分别有四种颜色的裙子可以搭配,如图:‎ 从图中可以看出,可供搭配的种类有3个4种,所以一共可以搭配出12套不同的衣服。‎ 这些服装一共可以搭配出12套不同的衣服。‎ ‎　　解题时,一定要分清是排列问题还是组合问题,本题是一道与顺序有关的排列题目。‎