2014金山区二模数学试卷

2014金山区二模数学试卷

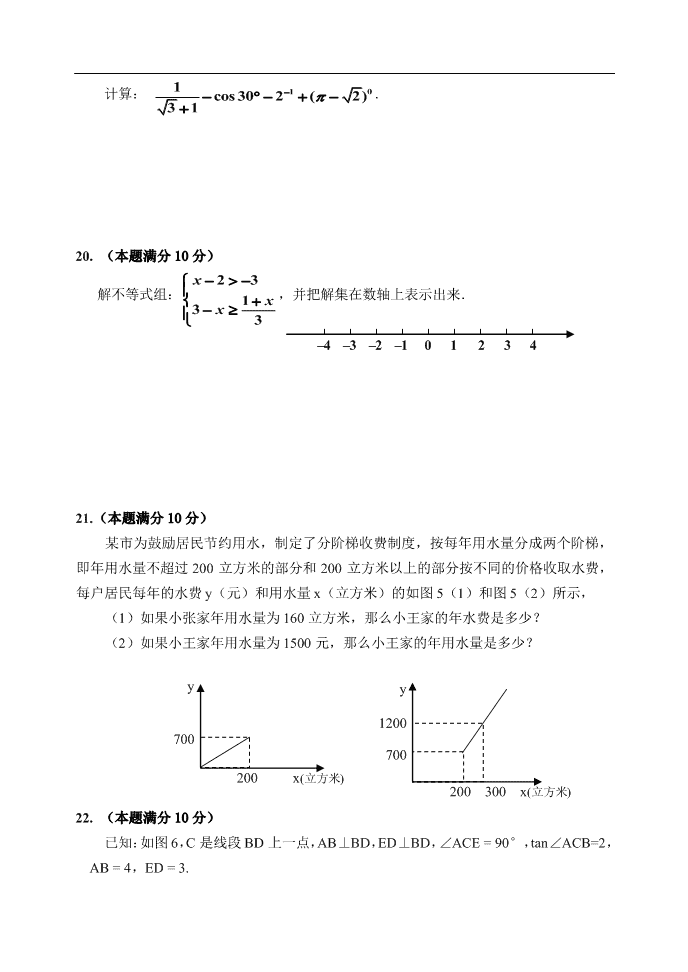
2013 学年第二学期金山区学习能力诊断卷 初中数学学科 2014.4 （满分 150 分，考试时间 100 分钟） 考生注意： 1. 本试卷含三个大题，共 25 题； 2. 答题时，考生务必按答题要求作答在答题纸规定位置，在草稿纸、本试卷上答题一律 无效； 3. 除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明 或计算的主要步骤. 一、选择题：（本大题共 6 题，每题 4 分，满分 24 分） 【四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答题纸相应位置上】 1. 下列各数中是有理数的是（ ） （A）3.14； （B） 8 ； （C） 2  ； （D） 2 2 ． 2. 将直线 2yx向下平移 2 个单位后，所得直线的解析式为（ ▲ ） （A） 4yx； （B） 2yx； （C） yx ； （D） 4yx． 3. 下列一元二次方程中有两个不相等的实数根的是（ ▲ ） （A） 2 10x  ； （B） 2 2 1 0xx   ； （C） 2 10xx   ； （D） 2 20x  4. 在本学期的“献爱心”的捐款活动中，九（1）班 学生捐款情况如图 1 所示，那么捐款金额的众数和 中位数分别是（ ▲ ）. （A）15 和 13.5； （B）8 元和 6.5 元； （C）15 和 8 元； （D）8 元和 8 元． 5. 下列命题中，真命题是（ ▲ ） （A）平行四边形是轴对称图形； （B）正多边形是中心对称图形； （C）正多边形都是轴对称图形； （D）是轴对称图形的四边形都是中心对称图形． 6. 在同一平面内，已知线段 AO = 2，⊙A 的半径为 r，将⊙A 绕点 O 按逆时针方向旋转 90°，得到的圆记作⊙B，如果⊙A 与⊙B 外切，那么 r，值为（ ▲ ） （A）1； （B）2； （C） 2 ； （D） 2 2 ． 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 7. 计算： 32()a = ▲ ． 8. 计算：( 2)( 2)aa   ▲ ． 9. 方程 2 1 11 x xx 的解是 ▲ ． 10. 计算： 2( )a a b   ▲ ． 11. 已知函数 2()fx x ，那么 ( 2)f  ▲ ． 12. 已知反比例函数的图像经过点（– 1 , 2），那么该反比例函数的图像的两个分支在第 ▲ 象限． 13. 菱形的两条对角线长分别是 6 和 8，这个菱形的周长为 ▲ ． 14. 某班共有学生 36 人，在迎新年庆祝会上，随机抽取 1 名一等奖，3 名二等奖，5 名三 等奖，以上统称为等第奖，该班每一名学生获得等第奖的概率是 ▲ ． 15. 为了了解学生课外阅读的喜好，某校随机抽取部分学生进行问卷调查，调查时要求每 人只选取一种喜欢的书籍，如果没有喜欢的书籍或者喜欢其他类型的书籍，则都选 “其他”，图 2 是整理数据后绘制的不完整的统计图，如果还知道喜欢漫画的有 60 人，选“其他”的有 30 人，那么喜欢小说的人数为 ▲ ． 16. 如图 3，在 ABC△ 中，AB = 4，BC = 6，BD 是∠ABC 的角平分线，DE // BC。DE 交 AB 于点 E，那么 DE 的长为 ▲ ． 17. 如果一个三角形的一边长等于另一边长的两倍，我们把这样的三角形成为“倍边三角 形”，如果一个直角三角形是倍边三角形，那么这个直角三角形的较小的锐角的正切 值为 ▲ . 18．如图 4，在 Rt 中， 90ACB  ， 4, 3AC BC，D 是边 AB 上一点，联 结 CD，把△ACD 沿 CD 所在的直线翻折，点 A 落在点 E 的位置，如果 DE∥BC， 那么 AD 的长为 ▲ . 其他10% 小说 漫画 科普 30% E D CB A 三、解答题：（本大题共 7 题，满分 78 分） 19. （本题满分 10 分） 图 4 图 2 第 14 题 第 15 题 图 3 C B A 计算： 101 cos30 2 ( 2) 31       . 20. （本题满分 10 分） 解不等式组： 23 13 3 x xx     ，并把解集在数轴上表示出来． 21.（本题满分 10 分） 某市为鼓励居民节约用水，制定了分阶梯收费制度，按每年用水量分成两个阶梯， 即年用水量不超过 200 立方米的部分和 200 立方米以上的部分按不同的价格收取水费， 每户居民每年的水费 y（元）和用水量 x（立方米）的如图 5（1）和图 5（2）所示， （1）如果小张家年用水量为 160 立方米，那么小王家的年水费是多少？ （2）如果小王家年用水量为 1500 元，那么小王家的年用水量是多少？ 22. （本题满分 10 分） 已知：如图 6，C 是线段 BD 上一点，AB⊥BD，ED⊥BD，∠ ACE = 90°，tan∠ACB=2， AB = 4，ED = 3. 30° –4 –3 –2 –1 0 1 2 3 4 y 700 200 x(立方米) y 1200 700 200 300 x(立方米) 求：（1）线段 BD 的长；（2）∠AEC 的正切值. E DCB A 23. （本题满分 12 分） 已知：如图 7，线段，AB∥CD，AC⊥CD，AC、BD 相交于点 P，E、F 分别是线段 BP 和 DP 的中点． （1） 求证：AE // CF； （2） 如果 AE 和 DC 的延长线相交于点 Q，M、N 分别 是线段 AP 和 DQ 的中点，求证：MN = CE． E F P D C BA 24. （本题满分 12 分） 如图，在直角坐标系中，直线 2yx与 x 轴交于点 A，B 是这条直线在第一象限 上的一点，过点 B、作 x 轴的垂线，垂足为点 D，已知△ABD 的面积为 18． （1）求点 B 的坐标； （2）如果抛物线 21 2y x mx n    的图像经过点 A 和点 B，求抛物线的解析式； （3）已知（2）中的抛物线与 y 轴相交于点 C，该抛物线对称轴与 x 轴交于点 H，P 是抛 物线对称轴上一点，过点 P 作 PQ // AC 交 x 轴交于点 Q，如果点 Q 在线段 AH 上， 并且 AQ = CP，求点 P 的坐标． 25. （本题满分 14 分） B A O D x y 如图，已知在梯形 ABCD 中，AD // BC，AB ⊥BC，AB = 4，AD = 3， 4sin 5DCB， P 是边 CD 上一点（点 P 与点 C、D 不重合），以 PC 为半径的⊙P 与边 BC 相交于点 C 和 点 Q． （1） 如果 BP⊥CD，求 CP 的长； （2） 如果 PA = PB，试判断以 AB 为直径的⊙O 与⊙P 的位置关系； （3） 联结 PQ，如果△ADP 和△BQP 相似，求 CP 的长． P D CB A D CB A 图 1 备用图