2009-2010数学一模试卷初三延庆

2009-2010数学一模试卷初三延庆

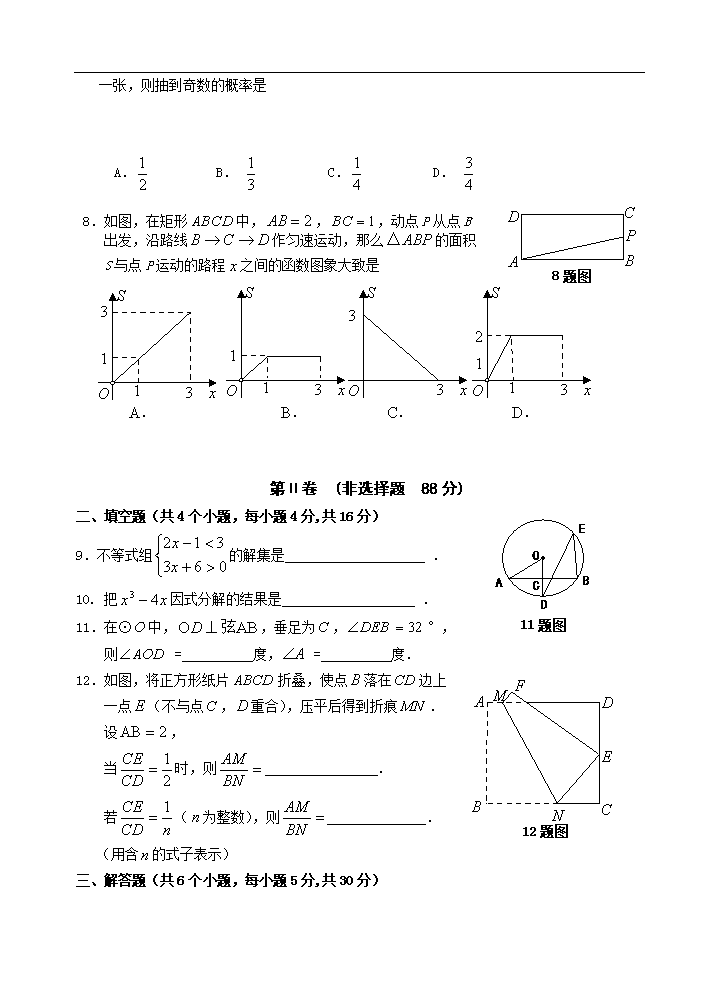
延庆县2010年毕业考试试卷 初 三 数 学 考生须知 ‎1.本试卷共6页，共五道大题，25道小题，满分120分。考试时间120分钟。‎ ‎2.在试卷和答题卡上认真填写学校名称、姓名和准考证号。‎ ‎3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。‎ ‎4.在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。‎ ‎5.考试结束，请将本试卷、答题卡和草稿纸一并交回。‎ 第Ⅰ卷 (选择题 32分)‎ 一、选择题：（共8个小题，每小题4分, 共32分）‎ 在下列每小题给出的四个选项中，只有一个是符合题目要求的，请在答题纸上将所选项涂黑。‎ ‎1．－2的倒数是 A． 2 B．－ C．-2 D．‎ ‎2．为迎接2010年上海世博会，将在全国招募志愿者。截止到2010年3月1日，约有610000人报名，将610000用科学记数法表示应为 A． B． C． D． ‎ ‎3．函数中，自变量的取值范围是 A． B． C． D． ‎ ‎4．下面四个图形中，是三棱柱的平面展开图的是 ‎ ‎ ‎5．初三年级某班十名男同学“俯卧撑”的测试成绩（单位：次数）分别是9，14，10，‎ ‎15，7，9，16，10，11，9，这组数据的众数、中位数依次是 ‎ A．9,10 B．10,‎11 ‎ C．9,11 D．10,9‎ ‎6．用配方法将代数式变形，结果正确的是 A． B． C． D． ‎ ‎7．下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，从中抽出 一张，则抽到奇数的概率是 A． B． C． D． ‎ D C P B A ‎8题图 ‎8．如图，在矩形中，，，动点P从点B 出发，沿路线作匀速运动，那么的面积 S与点P运动的路程之间的函数图象大致是 O ‎3‎ ‎1‎ ‎1‎ ‎3‎ S x A．‎ O ‎1‎ ‎1‎ ‎3‎ S x O ‎3‎ S x ‎3‎ O ‎1‎ ‎1‎ ‎3‎ S x B．‎ C．‎ D．‎ ‎2‎ 第Ⅱ卷 (非选择题 88分)‎ ‎11题图 二、填空题（共4个小题，每小题4分,共16分）‎ ‎9．不等式组的解集是 ．‎ ‎10. 把因式分解的结果是 ． ‎ ‎11．在⊙中，，垂足为，°，‎ 则 = 度， = 度．‎ ‎12题图 A B C D E F M N ‎12．如图，将正方形纸片折叠，使点落在边上 ‎ 一点（不与点，重合），压平后得到折痕．‎ 设，‎ 当时，则 ．‎ 若（为整数），则 ．‎ ‎（用含的式子表示）‎ 三、解答题（共6个小题，每小题5分,共30分）‎ ‎13．计算： ‎ ‎1‎ ‎2‎ ‎15题图 ‎14．计算： ‎ ‎15．已知：如图，，，，‎ 求证：‎ ‎16．已知：．求代数式的值．‎ ‎17题图 ‎17. 已知反比例函数的图象经过点A，若一次函数 的图象平移后经过该反比例函数图象上的点，‎ ‎（1）试确定反比例函数和m的值；‎ ‎（2）平移后的一次函数的表达式；‎ ‎（3）根据图象回答，在第一象限内，当取何值时，反比例 函数的值大于一次函数函数的值？‎ ‎18. 列方程或方程组解应用题：‎ ‎4月3日是首都第26个全民义务植树日，全民义务植树运动开展以来，我县大力实施工程造林及开展全民义务植树等社会造林活动，取得了显著成效。今年，市政公司为绿化西湖沿河风光带，计划购买五角枫、洋槐两种树苗共500株，五角枫每株50元，洋槐每株80元 ．若购买树苗预计用37000元，求五角枫、洋槐两种树苗各购买多少株？‎ 四、解答题（共4个小题，第19题5分，第20题5分，第21题4分，第22题4分，共18分）‎ ‎19. 如图，在梯形中，∥，，过 点作，交的延长线于点，且 ‎°，‎ 求的长．‎ ‎20．如图，为⊙的直径，平分交⊙于点，‎ 的延长线于点，交的延长 线于点，‎ ‎（1）求证：是⊙的切线；‎ ‎（2）若⊙的半径为5，求的长．‎ ‎21．为了了解延庆的旅游情况，小明收集了延庆县2007至2009年每年的旅游收入及旅游人数（其中缺少2009年入境旅游人数）的有关数据，整理并分别绘成图1，图2．‎ 旅游收入表 旅游收入统计图 ‎ ‎ 年份 ‎2007年 ‎2008年 ‎2009年 年旅游收入 ‎（亿元）‎ ‎54‎ ‎90‎ 根据上述信息，回答下列问题：‎ ‎（1）请你根据以上的信息补全 旅游收入表 ‎（请把结果填在答题卡上），并计算该地 区2007至2009年四年的年旅游收入的 平均数是 亿元；‎ ‎（2）据了解，该地区2008年、2009年旅游人数 的年增长率相同，那么2009年旅游人数是 万；‎ 并根据以上的信息，补全图2；‎ ‎（3）结合统计图和统计表，给县旅游局提一点积极的意见或建议．‎ ‎22．几何模型：‎ 条件：如下左图，、是直线同旁的两个定点．问题：在直线上确定一点，使的值最小．‎ 方法：作点关于直线的对称点，连结交于点，则的值最小（不必证明）．‎ 模型应用：‎ ‎（1） 如图1，正方形的边长为2，为的中点，是上一动点．连结，由正方形对称性可知，与关于直线对称．连结交于，则的最小值是___________；‎ ‎（2） 如图2，的半径为2，点在上，，，是 上一动点，则的最小值是___________；‎ ‎（3）如图3，，是内一点，，分别是上 A B ‎′‎ P l O A B P R Q 图3‎ O A B C 图2‎ A B E C P D 图1‎ P 的动点，则周长的最小值是___________．‎ 五、解答题（共3个小题， 23小题7分，24小题9分，25小题8分，共24分）‎ ‎23．已知: 关于的一元二次方程①.‎ ‎ （1）求证: 方程①有两个实数根;‎ ‎（2）求证: 方程①有两个实数根;‎ ‎（3）设方程①的另一个根为，若，为正整数且方程①有两个不相等的整数根时，确定关于的二次函数的解析式；‎ ‎（4）在（3）的条件下，把Rt△ABC放在坐标系内，其中∠CAB = 90°，点A、B的坐标分别为（1，0）、（4，0），BC = 5， 将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离。‎ ‎24. 如图，已知抛物线C1：的顶点为P，与x轴相交于A、B两点（点A在 点B的左边），点B的横坐标是1．‎ ‎（1）求P点坐标及a的值；‎ ‎（2）如图（1），抛物线C2与抛物线C1关于x轴对称，将抛物线C2向右平移，平移后的抛 物线记为C3，C3的顶点为M，当点P、M关于点B成中心对称时，求C3的解析式；‎ ‎（3）如图（2），点Q是x轴正半轴上一点，将抛物线C1绕点Q旋转180°后得到抛物线 C4．抛物线C4的顶点为N，与x轴相交于E、F两点（点E在点F的左边），当以点P、N、F为顶点的三角形是直角三角形时，求点Q的坐标．‎ y x A O B P M 图1‎ C1‎ C2‎ C3‎ 图24-1‎ y x A O B P N 图2‎ C1‎ C4‎ Q E F 图24-2‎ ‎25. 在图25-1至图25-3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和 CDHN都是正方形．AE的中点是M．‎ ‎（1）如图25-1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，‎ 求证：FM = MH，FM⊥MH；‎ ‎（2）将图25-1中的CE绕点C顺时针旋转一个锐角，得到图25-2，‎ 求证：△FMH是等腰直角三角形；‎ ‎（3）将图25-2中的CE缩短到图25-3的情况，△FMH还是等腰直角三角形吗？‎ G 图25-2‎ A H C D E B F N M ‎（不必说明理由）‎ 图25-1‎ A H C(M)‎ D E B F G(N)‎ A H C D E 图25-3‎ B F G M N 恭喜你，已经做完所有的题目，请再仔细地检查，可不要留遗憾噢！‎