中考数学三轮真题集训冲刺知识点37解直角三角形及其应用pdf含解析

中考数学三轮真题集训冲刺知识点37解直角三角形及其应用pdf含解析

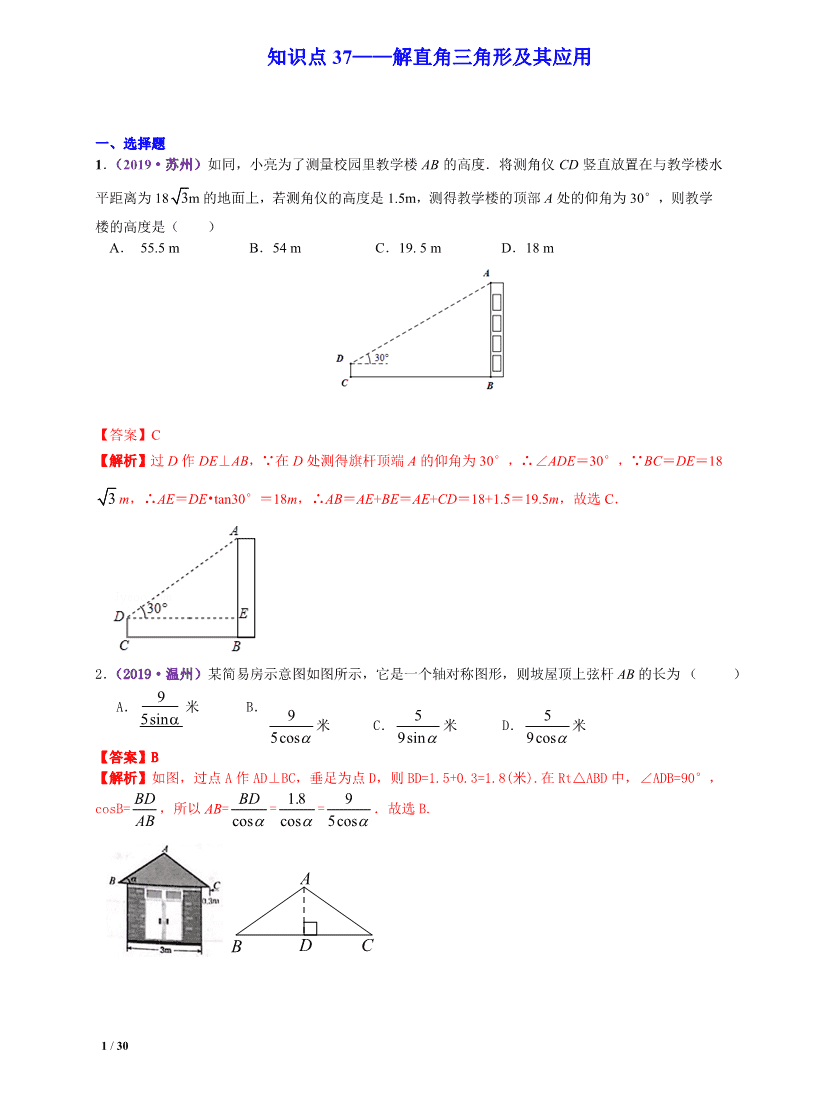
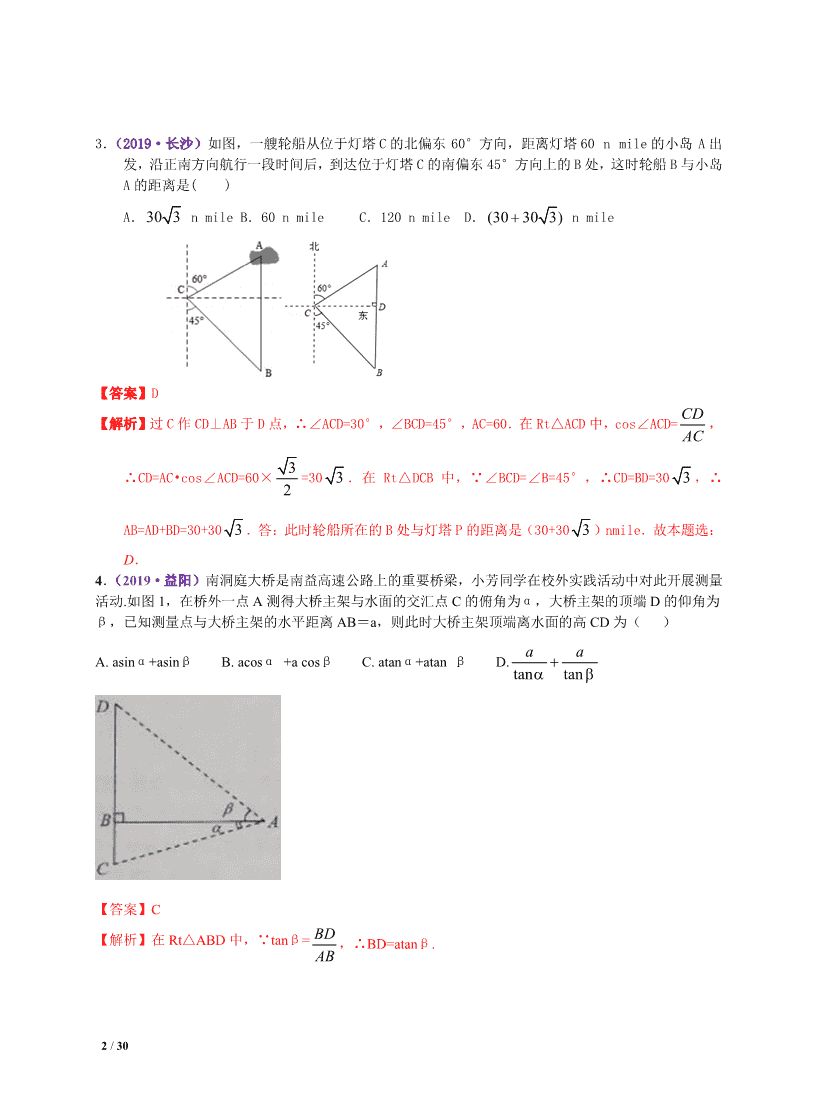
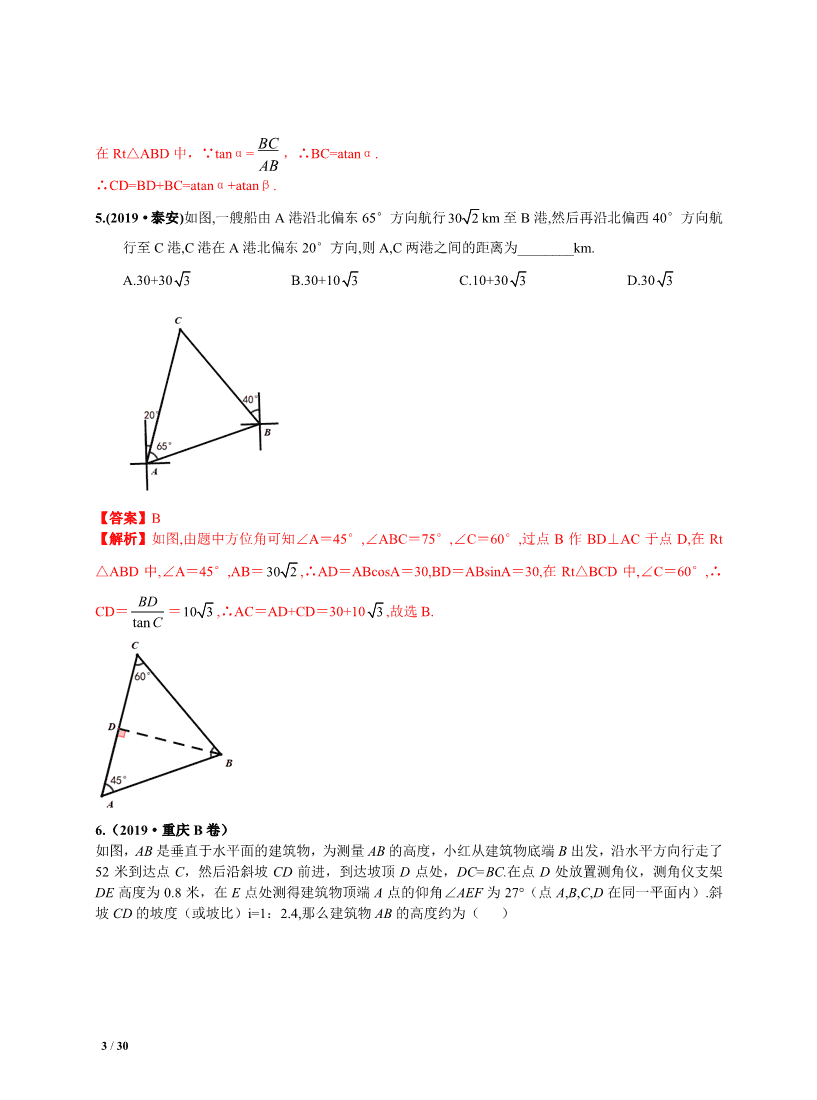
1 / 30 一、选择题 1．（2019·苏州）如同，小亮为了测量校园里教学楼 AB 的高度．将测角仪 CD 竖直放置在与教学楼水 平距离为 18 3m 的地面上，若测角仪的高度是 1.5m，测得教学楼的顶部 A 处的仰角为 30°，则教学 楼的高度是（ ） A． 55.5 m B．54 m C．19. 5 m D．18 m 【答案】C 【解析】过 D 作 DE⊥AB，∵在 D 处测得旗杆顶端 A 的仰角为 30°，∴∠ADE＝30°，∵BC＝DE＝18 3 m，∴AE＝DE•tan30°＝18m，∴AB＝AE+BE＝AE+CD＝18+1.5＝19.5m，故选 C． 2．（2019·温州）某简易房示意图如图所示，它是一个轴对称图形，则坡屋顶上弦杆 AB 的长为 （ ） A． 9 5sinα 米 B． 9 5cosα 米 C． 5 9sinα 米 D． 5 9cosα 米 【答案】B 【解析】如图，过点 A 作 AD⊥BC，垂足为点 D，则 BD=1.5+0.3=1.8(米).在 Rt△ABD 中，∠ADB=90°， cosB= BD AB ，所以 AB= cos BD α = 1.8 cosα = 9 5cosα ．故选 B. D CB A 知识点 37——解直角三角形及其应用 2 / 30 3．（2019·长沙）如图，一艘轮船从位于灯塔 C 的北偏东 60°方向，距离灯塔 60 n mile 的小岛 A 出 发，沿正南方向航行一段时间后，到达位于灯塔 C 的南偏东 45°方向上的 B 处，这时轮船 B 与小岛 A 的距离是( ) A．30 3 n mile B．60 n mile C．120 n mile D．(30 + 30 3) n mile 【答案】D 【解析】过 C 作 CD⊥AB 于 D 点，∴∠ACD=30° ，∠ BCD=45°，AC=60．在 Rt△ACD 中，cos∠ACD= CD AC ， ∴CD=AC•cos∠ACD=60× 3 2 =30 3 ．在 Rt△DCB 中，∵∠BCD=∠B=45°，∴CD=BD=30 3 ，∴ AB=AD+BD=30+30 3 ．答：此时轮船所在的 B 处与灯塔 P 的距离是（30+30 3 ）nmile．故本题选： D． 4．（2019·益阳）南洞庭大桥是南益高速公路上的重要桥梁，小芳同学在校外实践活动中对此开展测量 活动.如图 1，在桥外一点 A 测得大桥主架与水面的交汇点 C 的俯角为α，大桥主架的顶端 D 的仰角为 β，已知测量点与大桥主架的水平距离 AB＝a，则此时大桥主架顶端离水面的高 CD 为（ ） A. asinα+asinβ B. acosα +a cosβ C. atanα+atan β D. tanα tan β aa + 【答案】C 【解析】在 Rt△ABD 中，∵tanβ= AB BD ，∴BD=atanβ. 3 / 30 在 Rt△ABD 中，∵tanα= AB BC ，∴BC=atanα. ∴CD=BD+BC=atanα+atanβ. 5.(2019·泰安)如图,一艘船由 A 港沿北偏东 65°方向航行30 2 km 至 B 港,然后再沿北偏西 40°方向航 行至 C 港,C 港在 A 港北偏东 20°方向,则 A,C 两港之间的距离为________km. A.30+30 3 B.30+10 3 C.10+30 3 D.30 3 【答案】B 【解析】如图,由题中方位角可知∠A＝45°,∠ABC＝75°,∠C＝60°,过点 B 作 BD⊥AC 于点 D,在 Rt △ABD 中,∠A＝45°,AB＝30 2 ,∴AD＝ABcosA＝30,BD＝ABsinA＝30,在 Rt△BCD 中,∠C＝60°,∴ CD＝ tan BD C ＝10 3 ,∴AC＝AD+CD＝30+10 3 ,故选 B. 6.（2019·重庆 B 卷） 如图，AB 是垂直于水平面的建筑物，为测量 AB 的高度，小红从建筑物底端 B 出发，沿水平方向行走了 52 米到达点 C，然后沿斜坡 CD 前进，到达坡顶 D 点处，DC=BC.在点 D 处放置测角仪，测角仪支架 DE 高度为 0.8 米，在 E 点处测得建筑物顶端 A 点的仰角∠AEF 为 27°（点 A,B,C,D 在同一平面内）.斜 坡 CD 的坡度（或坡比）i=1：2.4,那么建筑物 AB 的高度约为（ ） 4 / 30 【答案】B 【解析】作 EN⊥AB 于 N,EM⊥BC 交 BC 的延长线于 M. ∵斜坡 CD 的坡度（或坡比）i=1：2.4, DC=BC=52 米，设 DM=x 米，则 CM=2.4x 米， 在 Rt△ECM 中，∵ 2DM + 2CM = 2DC ，∴ 2x +( )22.4x = 252 解得 x=20 ∴CM=48 米，EM=20+0.8=20.8 米，BM=ED+DM=52+48=100 米 ∵EN⊥AB,EM⊥BC，AB⊥BC∴四边形 ENBM 是矩形. ∴EN=BM=100 米，BN=EM=20.8 米. 在 Rt△AEN 中，∵∠AEF=27°∴AN=EN﹒tan27°≈100×0.51=51 米 ∴AB=AN+BN=51+20.8=71.8 米.故选 B． 7.（2019·重庆 A 卷）为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活 动．如图，在一个坡度（或坡比）i ＝1:2.4 的山坡 AB 上发现有一棵古树 CD．测得古树底端 C 到 山脚点 A 的距离 AC＝26 米，在距山脚点 A 水平距离 6 米的点 E 处，测得古树顶端 D 的仰角∠AED ＝48°（古树 CD 与山坡 AB 的剖面、点 E 在同一平面上，古树 CD 与直线 AE 垂直），则古树 CD 的高度约为（ ） （参考数据：sin 48 °≈0.73，cos48°≈0.67，tan48°≈1.11） A．17.0 米 B．21.9 米 C．23.3 米 D．33.3 米 【答案】C． 【解析】如答图，延长 DC 交 EA 于点 F，则 CF⊥EA．∵山坡 AC 上坡度i ＝1:2.4，AC＝26 米，∴令 CF＝k，则 AF＝2.4k，由勾股定理，得 k2＋(2.4k)2＝262，解得 k＝10，从而 AF＝24，CF＝10，EF＝30．在 Rt△DEF 中，tanE＝ DF EF ，故 DF＝EF•tanE＝30×tan48°＝30×1.11＝33.3，于是，CD＝DF－CF＝23.3， 故选 C． 二、填空题 1.（2019·遂宁）汛期即将来临，为保证市民的生命和财产安全，市政府决定对一段长 200 米且横断 面为梯形的大坝用土石进行加固，如图，加固前大坝背水坡坡面从 A 至 B 共有 30 级阶梯，平均每级阶 梯高 30cm，斜坡 AB 的坡度 i=1:1，加固后坝顶宽度增加 2 米，斜坡 EF 的坡度 i=1: 5 ,问工程完工后， 共需土石多少立方米？（计算土石时忽略阶梯，结果保留根号） F ED B A C 5 / 30 解：如图，分别过点 A,E 作 AN⊥FC 于 N,EM⊥F 于 M， 则 AN=EM, ∵从 A 至 B 共有 30 级阶梯，平均每级阶梯高 30cm， ∴AN=9 米=EM， ∵斜坡 AB 的坡度 i=1:1， ∴BN=AN=9 米， ∵斜坡 EF 的坡度 i=1: 5 ， ∴FM=9 5 ， ∴FB=FM+MN-BN=9 5 +2-9=9 5 -7, S 梯= EMBFAE ×+ )2 1（ = 2 4552 819)75922 1 −=×−+（ , ∴体积为 200S 梯=8100 5 -4500（m3) 答:共需土石 8100 5 -4500 立方米. 2．(2019·广元)如图,某海监船以 60 海里时的速度从 A 处出发沿正西方向巡逻,一可疑船只在 A 的西北 方向的 C 处,海监船航行 1.5 小时到达 B 处时接到报警,需巡查此可疑船只,此时可疑船只仍在 B 的北偏西 30°方向的 C 处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以 90 海里/时的速度追击, 在 D 处海监船追到可疑船只,D 在 B 的北偏西 60°方向.(以下结果保留根号) (1)求 B,C 两处之间的距离; (2)求海监船追到可疑船只所用的时间. 解：(1)过点 C 作 CE⊥AB 于点 E,在 Rt△BEC 中,设 BC＝x,∵∠BCE＝30°,∴BE＝ 1 2 BC＝ 1 2 x,CE＝ 3 2 x,在 Rt△ACE 中,AE＝CE＝ 3 2 x,∴AB＝AE－BE＝ 3 2 x－ 1 2 x,已知 AB＝60×1.5＝90,∴ 3 2 x－ 1 2 x＝ 90,解之得,x＝90 3 +90.答:B,C 两处之间的距离(90 3 +90)海里; 6 / 30 (2)过点 B 作 BF⊥DC 于点 F,在 Rt△BDF 中,∠DBF＝60°,由(1)得,BF＝CE＝CE＝ 3 2 x＝135+45 3 , ∴BD＝2BF＝270+90 3 ,∴时间为(270+90 3 )÷90＝3+ 3 .答:海监船追到可疑船只所用的时间为(3+ 3 )小时. 3．（2019·温州）图 1 是一种折叠式晾衣架．晾衣时，该晾衣架左右晾衣臂张开后示意图如图 2 所示， 两 支脚 OC=OD=10 分米，展开角∠COD=60°，晾衣臂 OA=OB=10 分米，晾衣臂支架 HG=FE=6 分米，且 HO=FO=4 分米．当∠AOC=90°时，点 A 离地 面的距离 AM 为 分米；当 OB 从水平状态旋转到 OB′（在 CO 延长线上）时，点 E 绕点 F 随之旋转至 OB′ 上的点 E′处， 则 B′E′-BE 为 分米． 【答案】5+5 3 4 【解析】（1）过点 O 分别作 OL⊥MD、ON⊥AM， 垂 足 分 别 为 点 L、N，则∠LON=90°，四边形 NMLO 是矩形，∴MN=LO. ∵OC=OD=10 分米，∠COD=60°，∴∠COL=30°， CL= 1 2 CD=5，OL= 22-OC CL = 2210 -5 =5 3 ，∵∠AOC=90°，∴∠AON=30° ，∴AN= 1 2 AO=5，∴AM=5+5 3 ；（2）过点 F 分别作 FQ⊥OB、FP⊥OC，垂足分别为点 Q、N. 在 Rt△OPQ 中 ，∠ OQP=90° ，∠ BOD=60°， ∴OQ=2，FQ=2 3 ，在 Rt△EFQ 中 ，∠ EQF=90°，FQ=2 3 ，EF=6，∴ QE=2 6 ，BE=10-2-2 6 =8-2 6 ； 同理可得 PE′=2 6 ，∴B′E′=2+10-2 6 =12-2 6 ，∴B′E′-BE=(12-2 6 )-(8-2 6 )=4. 故填： 5+5 3 4. F E 7 / 30 4．（2019·盐城）如图，在△ABC 中，BC＝ 6 + 2 ，∠C＝45°，AB＝ 2 AC，则 AC 的长为________. 【答案】2 【解析】如图，过点 A 作 AD⊥BC 于点 D，又 ∠C＝45°，故 2sin 2 ADC AC = = , tan 1ADC CD = = ，设 AD x= ， 则 22AC AD x= = ，CD=x， 22AB AC x= = ，在 Rt△ACD 中，∠ADB=90°，由勾股定理可得： AD2+BD2=AB2，得 3BD x= ，所以 3+ 6 2BC BD CD x=+= =+（ 1） ，解得 2x = ,故 AC=2. 5.(2019·枣庄)如图,小明为了测量校园里旗杆 AB 的高度,将测角仪 CD 竖直放在距旗杆底部 B 点 6m 的 位置,在D处测得旗杆顶端A的仰角为53°,若测角仪的高度是1.5m,则旗杆AB的高度约为________m(精 确到 0.1m).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) A B C D A B C 8 / 30 【答案】9.5 【解析】由题可知 BC＝6m,CD＝1.5m,过 D 作 DE∥BC 交 AB 于点 E,易知四边形 BCDE 是矩形,∴DE＝ BC＝6m,在 Rt△ADE 中,AE＝DE·tan53°＝7.98m,EB＝CD＝1.5m,∴AB＝AE+EB＝9.48m≈9.5m. 6.（2019·湖州）有一种落地晾衣架如图①所示，其原理是通过改变两根支撑杆夹角的度数来调整晾衣 杆的高度．图②是支撑杆的平面示意图．AB 和 CD 分别是两根不同的支撑杆，夹角∠BOD＝α．若 AO＝85cm，BO＝DO＝65cm．问：当 α＝74°时，较长支撑杆的端点 A 离地面的高度 h 约为 ________cm．（参考数据：sin37°≈0.6，cos37°≈0.8，sin53°≈0.8，cos53°≈0.6） 【答案】120． 【解析】如图，过点 A 作 AE⊥BD 于点 E，则∠AEB＝90°． ∵AO＝85cm，BO＝DO＝65cmα＝74°， ∴∠ODB＝∠B＝53°，AB＝150cm． 在 Rt△ABE 中，sinB＝ h AB ， 故 h＝AB•sinB＝150×sin53°≈150×0.8＝120． 7.（2019·金华）如图，在量角器的圆心 O 处下挂一铅锤，制作了一个简易测倾仪，量角器的 0 刻度线 AB 对准楼顶时，铅垂线对应的度数是 50°，则此时观察楼顶的仰角度数是___________． 9 / 30 【答案】40°． 【解析】量角器的 0 刻度线 AB 对准楼顶时，铅垂线对应的度数是 50°，则过 AB 中点的水平线对应的是 140°，所以此时观察楼顶的仰角度数是 40°． 8.（2019·金华）图 2，图 3 是某公共汽车双开门的俯视示意图，ME、EF、FN 是门轴的滑动轨道，∠ E=∠F=90°，两门 AB、CD 的门轴 A、B、C、D 都在滑动轨道上，两门关闭时（图 2），A、D 分别在 E、 F 处，门缝忽略不计（即 B、C 重合）；两门同时开启，A、D 分别沿 E→M，F→N 的方向匀速滑动，带 动 B、C 滑动；B 到达 E 时，C 恰好到达 F，此时两门完全开启，已知 AB=50cm，CD=40cm. （1）如图 3，当∠ABE=30°时，BC=_______cm. （2）在（1）的基础上，当 A 向 M 方向继续滑动 15cm 时，四边形 ABCD 的面积为_______cm2. 【答案】（1）（ 90－45 3 ）；（2）2256． 【解析】（1）利用直角三角形的性质先求得 EB，CF，然后进行线段加减即可； （2）根据题意，得 S 四边形 ABCD＝S 梯形 AEFD－S △ ABE－S △ CDF，计算可得. 解：(1)∵ AB=50，CD=40，∴AB＋CD= EB＋CF＝EF=90. 在 Rt △ ABE 中，∵∠E =90°，∠ABE=30°，∴EB＝25 3 . 同理可得 CF＝20 3 .∴BC=90－45 3 （cm）. （2）根据题意，得 AE＝40, DF=32, EB＝ 2250 40− ＝30，CF＝ 2240 32− ＝24, ∴S 四边形 ABCD＝S 梯形 AEFD－S △ ABE－S △ CDF ＝ 1 2 (AE＋DF)·EF－ 1 2 AE·EB－ 1 2 CF·DF ＝ 1 2 (40＋32)×90－ 1 2 ×40×30－ 1 2 ×24×32 ＝2256. 图3图2图1 DA N B(C) N E(A) EF(D) M F M B C 10 / 30 9. (2019·宁波)如图,某海防哨所 O 发现在它的西北方向,距离哨所 400 米的 A 处有一艘船向正东方向航 行,航行一段时间后到达哨所北偏东 60°方向的 B 处,则此时这艘船与哨所的距离 OB 约为________ 米. 【答案】566 【解析】在 Rt△AOH 中,OH＝AOcos45°＝ 200 2 ,在 Rt△BOH 中,BO＝ 400 2 566cos60 OH = ≈ . 10.（2019·衢州）如图，人字梯 AB，AC 的长都为 2 米，当α=50°时，人字梯顶端离地面的高 度 AD 是米_________（结果精确到 0.1m 参考数 据；sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）. 【答案】1.5 【解析】由三角函数的定义得:sinα= sin50°= AD AC = 2 AD ≈0.77，所以 AD≈2×0.77=1.54≈1.5 米. 三、解答题 1.（2019 年浙江省绍兴市，第 20 题，8 分 如图 1 为放置在水平桌面 l 上的台灯，底座的高 AB 为 5cm， 长度均为 20cm 的连杆 BC，CD 与 AB 始终在同一平面上． （1）转动连杆 BC，CD，使∠BCD 成平角，∠ABC＝150°，如图 2，求连杆端点 D 离桌面 l 的高度 DE． 11 / 30 （2）将（1）中的连杆 CD 再绕点 C 逆时针旋转，使∠BCD＝165°，如图 3，问此时连杆端点 D 离桌 面 l 的高度是增加还是减少？增加或减少了多少？（精确到 0.1cm，参考数据： 73.13,41.12 ≈≈ ） 【解题过程】 2．（2019·嘉兴）某挖掘机的底座高 AB＝0.8 米，动臂 BC＝1.2 米，CD＝1.5 米，BC 与 CD 的固定夹角 ∠BCD＝140°．初始位置如图 1，斗杆顶点 D 与铲斗顶点 E 所在直线 DE 垂直地面 AM 于点 E，测得∠ CDE＝70°（示意图 2）．工作时如图 3，动臂 BC 会绕点 B 转动，当点 A，B，C 在同一直线时，斗杆顶 12 / 30 点 D 升至最高点（示意图 4）． （1）求挖掘机在初始位置时动臂 BC 与 AB 的夹角∠ABC 的度数． （2）问斗杆顶点 D 的最高点比初始位置高了多少米（精确到 0.1 米）？ （参考数据：sin50°≈0.77，cos50°≈0.64，sin70°≈0.94，cos70°≈0.34， 1.73） 【解题过程】（1）如图 2-1，过点 C 作 CG⊥AM 于点 G，∵AB⊥AM，DE⊥AM，∴AB//DE//CG ∴∠DCG=180°-∠CDE=110°. ∴∠BCG=∠BCD -∠DCG=30°. ∴∠ABC=180°-∠BCG=150°. ∴动臂 BC 与 AB 的夹角为 150°. （2）如图 2-2，过点 C 作 CP⊥DE 于点 P，过点 BQ⊥DE 于点 Q 交 CG 于点 N. 在 Rt△CPD 中，DP=CD×cos70°=0.51（米） 在 Rt△BCN 中，CN=BC×sin60° ≈1.04（米） ∴DE=DP+PQ+QE=DP+CN+AB ≈2.35（米） 如图 3，过点 D 作 DH⊥AM 于点 H，过点 C 作 CK⊥DH 于点 K. 在 Rt△CKD 中，DK=CD×sin5° ≈1.16（米） ∴DH=DK+KH ≈3.16（米） ∴DH-DE ≈0.8（米）. 所以斗杆顶点 D 的最高点比初始位置高了约 0.8 米. 13 / 30 3.（2019 浙江省杭州市，23，12 分）(本题满分 12 分) 如图，已知锐角三角形 ABC 内接于⊙O，OD⊥BC 于点 D.连接 0A. (1)若∠BAC=60°， ①求证：OD= 1 2 OA. ②当 OA=1 时，求△ABC 面积的最大值. (1) 点 E 在线段 0A 上.OE=OD.连接 DE，设∠ABC=m∠OED.∠ACB=n∠OED(m，n 是正数). 若∠ABC＜∠ACB.求证:m-n+2=0 【解题过程】（1）①连接 OB、OC， 则∠BOD= BOC=∠BAC=60°， ∴∠OBC=30°， ∴OD= 1 2 OB= 1 2 OA； ②∵BC 长度为定值， ∴△ABC 面积的最大值，要求 BC 边上的高最大， 当 AD 过点 O 时，AD 最大，即：AD=AO+OD= 3 2 ， △ABC 面积的最大值= 1 2 ×BC×AD= 1 2 ×2OBsin60°× 3 2 = 33 4 ； （2）如图 2，连接 OC， 设∠OED=x，则∠ABC=mx，∠ACB=nx， 则∠BAC=180°-∠ABC-∠ACB=180°-mx-nx= 1 2 ∠BOC=∠DOC， ∵∠AOC=2∠ABC=2mx，∴∠AOD=∠COD+∠AOC=180°-mx-nx+2mx=180°+mx-nx， 14 / 30 ∵OE=OD，∴∠AOD=180°-2x，即：180°+mx-nx=180°-2x，化简得：m-n+2=0． 4．（2019 山东烟台，23，10 分） 如图所示，一种适用于笔记本电脑的铝合金支架，边 OA，OB 可绕点 O 开合，在 OB 边上有一固定 点 P，支柱 PQ 可绕点 P 转动，边 OA 上有六个卡孔，其中离点 O 最近的卡孔为 M，离点 O 最远的 卡孔为 N．当支柱端点 Q 放入不同卡孔内，支架的傾斜角发生変化．将电脑放在支架上，电脑台面 的角度可达到六档调节，这样更有利于工作和身体健康．现测得 OP 的长为 12 cm ，OM 为 10cm， 支柱 PQ 为 8cm． (1)当支柱的端点 Q 放在卡孔 M 处时，求∠AOB 的度数． (2)当支柱的端点 Q 放在卡孔 N 处时，∠AOB = 20.5° ，若相邻两孔的距离相等，求此间距．（结果 精确到十分位）． 【解题过程】 （1）解：当支柱的端点 Q 放在卡孔 M 处时，作出该支架的截面图如图（1）， 15 / 30 过点 P 作 PE OA⊥ ，垂足为 E， 此时， 12OP = ， 10OM OQ= = ， 8PQ = ， 因为 PE OA⊥ ， 所以 90OEP PEQ∠=∠=°， 设OE x= ，所以 10EQ OQ OE x=−=−， 在 Rt△OPE 中，由勾股定理得， 2 22PE OP PE= − 2212 x= − ， 在 Rt△PEQ 中，由勾股定理得， 2 22PE PQ EQ= − 228 (10 )x=−−， 所以 222 212 8 (10 )xx−=− − ，解得 9x = ， 所以 9OE = , 在 Rt△OPE 中， 9cos 0.4512 OEAOB OP ∠===, 由参考数据表，可得， 41AOB∠=°． （2）解：当支柱的端点 Q 放在卡孔 N 处时，作出该支架的截面图如图（2）， 过点 P 作 PE OA⊥ ，垂足为 F， O A Q(M) P E B O A Q(N) P F B 第 4 题答图(1) 第 4 题答图（2） 16 / 30 此时， 12OP = ，ON OQ= ， 8PQ = ， 20.5AOB∠=°， 因为 PE OA⊥ ， 所以 90OEP PEQ∠=∠=°， 在 Rt△OPE 中， sin PEAOB OP ∠=， 所以 sin sin 20.5 12 0.45 4.2PE OP AOB OP= × ∠ = × °= × = ， 在 Rt△PEQ 中，由勾股定理得， 22228 4.2 46.36 6.8FQ PQ PE= −=−= =， 在 Rt△OPE 中，由勾股定理得， 22 2212 4.2 126.36 11.24OF OP PE= −= −= = 2212 x= − ， 所以 11.24 6.8 18.04ON OF FQ= + = += ， 所以 18.04 10 1.655 ON OMd −−= = ≈ , 【解题过程】∵BH＝0.6，sinα＝ ， ∴AB＝ ＝1， ∴AH＝0.8， ∵AF＝FC＝2，∴BF＝1， 作 FQ⊥BG 于点 Q，作 EP⊥FQ 于点 P， ∵EF＝FB＝AB＝1，∠EPF＝∠FQB＝∠AHB＝90°，∠EFP＝∠FBQ＝∠ABH， 所以相邻两孔的距离为 1.6cm ． 5.（2019 山东威海，22，9 分）如图是把一个装有货物的长方体形状的木箱沿着坡面装进汽车货厢的示 意图．已知汽车货厢高度 BG＝2 米，货厢底面距地面的高度 BH＝0.6 米，坡面与地面的夹角∠BAH＝α， 木箱的长（FC）为 2 米，高（EF）和宽都是 1.6 米．通过计算判断：当 sinα＝ ，木箱底部顶点 C 与 坡面底部点 A 重合时，木箱上部顶点 E 会不会触碰到汽车货厢顶部． 3 5 3 5 0.6 3sin 5 BH α = 17 / 30 ∴△EFP≌△FBQ≌△ABH， ∴EP＝FQ＝AH，BQ＝BH， ∴BQ＋EP＝0.6＋0.8＝1.4（米）＜2 米， ∴木箱上部顶点 E 不会触碰到汽车货厢顶部． 6．（2019 江西省，20，8 分）图 1 是一台实物投影仪，图 2 是它的示意图，折线 B—A—O 表示固定支 架，AO 垂直水平桌面 OE 于点 O，点 B 为旋转点，BC 可转动，当 BC 绕点 B 顺时针旋转时，投影探头 CD 始终垂直于水平桌面 OE，经测量：AO＝6.8cm，CD＝8cm，AB＝30cm，BC＝35cm.(结果精确到 01) (1)如图 2，∠ABC＝70°，BC∥OE. ①填空：∠BAO＝ °； ②求投影探头的端点 D 到桌面 OE 的距离. (2)如图 3，将(1)中的 BC 向下旋转，当投影探头的端点 D 到桌面 OE 的距离为 6cm 时，求∠ABC 的大 小. (参考数：sin70°≈0.94，cos20°≈0.94，sin36.8°≈0.60，cos53.2°≈0.60) 【解题过程】解：（1）①如图所示，延长 OA 交 BC 于点 F， ∵BC∥OE，OA⊥OE， ∴∠BFA=∠AOE=90°， ∴∠BAO=∠BFA+∠ABC=90°+70°=160°. 答案：160 ②∵∠BFA=90°，∠ABC=70°，AB＝30cm，sin70°≈0.94， ∴AF=AB·sin70°≈30×0.94=28.2（cm）. ∵OA=6.8cm， ∴OF=AF+OA=28.2+6.8=35（cm）. 又∵CD 始终垂直于水平桌面 OE，且 CD＝8cm， 18 / 30 ∴点 D 到桌面 OE 的距离为：OF-CD=35-8=27（cm）. （2）如图所示，作 BH⊥CD 于点 H， ∵D 到桌面 OE 的距离为 6cm，H 到桌面 OE 的距离为 35cm，CD＝8cm， ∴CH=35-8-6=21（cm）， 又∵BC＝35cm，∠H=90°， ∴sin∠CBH= 6.05 3 35 21 === BC CH ， ∵sin36.8°≈0.60， ∴∠CBH=36.8°. 又∵∠ABH=70°, ∴∠ABC=∠ABH-∠CBH=70°-36.8°=33.2°. 7．（2019·山西）某"综合与实践"小组开展了测量本校旗杆高度的实践活动.他们制定了测量方案,并利 用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端 的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离 时,都分别测量了两次并取他们的平均值作为测量结果,测量数据如下表(不完整). 课题 测量旗杆的高度 成员 组长:××× 组员:×××,×××,××× 测量工具 测量角度的仪器,皮尺等 测量 示意图 说明:线段 GH 表示旗杆,测量角度的仪器的高度 AC＝BD＝1.5m,测点 A,B 与 H 在同一条水平直线上,A,B 之间的距离可以直接测得,且点 G,H,A,B,C,D 都在同一竖直平面内.点 C,D,E 在同一直线上,点 E 在 GH 上. 测量数据 测量项目 第一次 第二次 平均值 ∠GCE 的度数 25.6° 25.8° 25.7° ∠GDE 的度数 31.2° 30.8° 31° A,B 之间的距离 5.4m 5.6m …… …… 任务一:两次测量 A,B 之间的距离的平均值是______m. 19 / 30 任务二:根据以上测量结果,请你帮助该"综合与实践"小组求出学校旗杆 GH 的高度. (参考数据:sin25.7°≈0.43,cos25.7°≈0.90,tan25.7°≈0.48,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60) 任务三:该"综合与实践"小组在制定方案时,讨论过"利用物体在阳光下的影子测量旗杆的高度"的方案,但 未被采纳.你认为其原因可能是什么?(写出一条即可) 【解题过程】任务一:平均值＝(5.4+5.6)÷2＝5.5m 任务二:由题意可得,四边形 ACDB,ACEH 都是矩形,∴EH＝AC＝1.5,CD＝AB＝5.5,设 EG＝xm,在 Rt△ DEG 中,∠DEG＝90°,∠GDE＝31°,∵tan31°＝ EG DE ,∴DE＝ tan 31 x  ,在 Rt△CEG 中,∠CEG＝90°,∠ GCE＝25.7°,∵tan25.7°＝ EG CE ,∴CE＝ tan 25.7 x  ,∵CD＝CE－DE,∴ tan 25.7 x  － tan 31 x  ＝5.5,∴x＝ 13.2,∴GH＝GE+EH＝13.2+1.5＝14.7.答:旗杆 GH 的高度为 14.7m. 任务三:答案不唯一:没有太阳光,旗杆底部不可到达,测量旗杆影子的长度遇到困难等. 8．（2019·娄底）如图（11），某建筑物 CD 高 96 米，它的前面有一座小山，其斜坡 AB 的坡度为 i＝ 1:1．为了测量山 顶 A 的高度，在建筑物顶端 D 处测得山顶 A 和坡底 B 的俯角分别为α ， β ．已 知 tanα = 2 ， tan β = 4 ，求山顶 A 的高度 AE（C、B、E 在同一水平面上）． 解：如图（11－1）， 设 DA 与 CB 的交点为 O． ∵ 96tan tan 2DCO OC OC α∠= = = =， ∴ 48OC = 同理，∵ 96tan tan 4DCDBC BC BC β∠= === ∴ 24BC = ． ∴ 48 24 24OB OC BC= − =−=． 设 AE x= 米,则 则由 i＝1:1 得 BE x= , 1 2OE x= ； 20 / 30 ∴ 1 242xx+=， ∴ 16x = ∴山顶 A 的高度 AE 为 16 米． 9．（2019·衡阳）如图，在一次综合实践活动中，小亮要测量一楼房的高度，先在坡面 D 处测得楼房 顶部 A 的仰角为 30°，沿坡面向下走到坡脚 C 处，然后向楼房方向继续行走 10 米到达 E 处，测得楼房 顶部 A 的仰角为 60°，已知坡面 CD＝10 米，山坡的坡度 i＝1： 3 ，(坡度 i 是指坡面的铅直高度与水 平宽度的比)，求楼房 AB 高度.（结果精确到 0.1 米）（参考数据： 3 ≈1.73， 2 ≈1041） 解：设楼房 AB 的高为 x 米，则 EB＝ 3 3 x， ∵坡度 i＝1: 3 ，∴坡面 CD 的铅直高度为 5 米，坡面的水平宽度为53米， ∴ 35 3 10 3( 5)+ + 3 x = x − ， 解得 x＝15＋5 3 ≈237（米）. 所以楼房 AB 的高度约为 237 米. 10．(2019·泰州,21 题,10 分)某体育看台侧面的示意图如图所示,观众区 AC 的坡度 i 为 1∶2,顶端 C 离水 平地面AB的高度为10m,从顶棚的D 处看E处的仰角α＝18°30′,竖直的立杆上C、D 两点间的距离为4m,E 30° 60° 楼 房 i＝1： 3 B A C D E 21 / 30 处到观众区底端 A 处的水平距离 AF 为 3m,求: ⑴观众区的水平宽度 AB; ⑵顶棚的 E 处离地面的高度 EF. (sin18°30′≈0.32,tan18°30′≈0.33,结果精确到 0.1m) 【解题过程】(1)因为 AC 的坡度 i 为 1∶2,所以 1 2 CB AB = ,因为 BC＝10m,所以 AB＝20m; (2)在 Rt△DEG 中,∠EDG＝18°30′,tan∠EDG＝ EG GD ,GD＝FB＝FA+AB＝23m,所以 EG＝7.59m,所以 EF＝ EG+GF＝EG+DB＝EG+DC+CB＝21.59≈21.6m,顶棚的 E 处离地面的高度 EF 为 21.6m. 第 10 题答图 11.（2019·黄冈）如图，两座建筑物的水平距离BC为40m，从A点测得D点的俯角α为45°，测得C点的 俯角β为60°.求这两座建筑物AB，CD的高度.（结果保留小数成后一位， 2 ≈1.414， 3 /≈1.732.） 22 / 30 【解题过程】 12．（2019·陇南）图 ① 是放置在水平面上的台灯，图 ② 是其侧面示意图（台灯底座高度忽略不计）， 其中灯臂 AC＝40cm，灯罩 CD＝30cm，灯臂与底座构成的∠CAB＝60°．CD 可以绕点 C 上下调节 一定的角度．使用发现：当 CD 与水平线所成的角为 30°时，台灯光线最佳．现测得点 D 到桌面的 距离为 49.6cm．请通过计算说明此时台灯光线是否为最佳？（参考数据： 取 1.73）． 解：如图，作 CE⊥AB 于 E，DH⊥AB 于 H，CF⊥DH 于 F． 23 / 30 ∵∠CEH＝∠CFH＝∠FHE＝90°， ∴四边形 CEHF 是矩形， ∴CE＝FH， 在 Rt△ACE 中，∵AC＝40cm，∠A＝60°， ∴CE＝AC•sin60°＝34.6（cm）， ∴FH＝CE＝34.6（cm） ∵DH＝49.6cm， ∴DF＝DH﹣FH＝49.6﹣34.6＝15（cm）， 在 Rt△CDF 中，sin∠DCF＝ ＝ ＝ ， ∴∠DCF＝30°， ∴此时台灯光线为最佳． 13．（2019·株洲）小强的爸爸准备驾车外出．启动汽车时，车载报警系统显示正前方有障碍物，此时 在眼睛点 A 处测得汽车前端 F 的俯角为α ，且 tanα ＝ 1 3 ，若直线 AF 与地面 l1 相交于点 B，点 A 到地面 l1 的垂线段 AC 的长度为 1.6 米，假设眼睛 A 处的水平线 l2 与地面 l1 平行． （1）求 BC 的长度； （2）假如障碍物上的点 M 正好位于线段 BC 的中点位置（障碍物的横截面为长方形，且线段 MN 为此长方形前端的边）， MN⊥l1，若小强的爸爸将汽车沿直线 l1 后退 0.6 米，通过汽车的前端 F 点恰好看见障碍物的顶部 N 点（点 D 为点 A 的对应点，点 F1 为点 F 的对应点）．求障碍物 的高度． 【解题过程】 24 / 30 (1) 如图， ∵l1∥l2 ∴∠ABC=α ∴tan∠ABC= AC BC =tanα ＝ 1 3 ， ∴BC=3AC= =×3 1.6 4.8(米） ∴BC 的长度为 4.8 米。 （2) 根据题意得 DF1∥AF, ∵l1∥l2∴四边形 ABED 是平行四边形， ∴BE=BM=FF1=0.6(米 ）， ∴EM=BM-BE= 1 2 BC-BE=2.4-0.6=1.8（米）, ∵tan∠NEM=tan∠ABC= 1 3 ， ∴MN= 1 3 EM=0.6（米） ∴障碍物的高度为 0.6 米. 14.(2019·台州)图 1 是一辆在平地上滑行的滑板车,图 2 是其示意图,已知车杆 AB 长 92cm,车杆与脚踏 所 成的角∠ABC＝70°,前后轮子的半径均为 6cm,求把手 A 离地面的高度.(结果保留小数点后一位;参 考数 据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75) 解：过点 A 作 AD⊥BC 于点 D, 在 Rt△ABD 中,AB＝92,∠B＝70°, ∴AD＝ABsinB＝86.48, ∴A 离地面高度为 86.48+6≈92.5(cm). 25 / 30 答：求把手 A 离地面的高度 92.5cm. 15.（2019·天津）如图，海面上一艘船由西向东航行，在 A 处测得正东方向上一座灯塔的最高点 C 的 仰角为 31°，再向东继续航行 30m 到达 B 处，侧的灯塔的最高点 C 的仰角为 45°，根据测得的数据，计 算 这座灯塔的高度 CD.（结果保留整数）参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60 解：如图，根据题意∠CAD=31°，∠CBD=45°，∠CDA=90°，AB=30， ∵在 Rt△ACD 中，tan∠CAD= CD AD ∴AD= tan 31 CD  ∵在 Rt△BCD 中，tan∠CBD= CD BD , ∴BD= tan 45 CD CD= ， ∵AD=BD+AB, ∴ tan 31 CD  =30+CD,∴CD=45. 答：这座灯塔的高度 CD 约为 45m. 16.（2019·眉山）如图，在岷江的右岸边有一高楼 AB，左岸边有一坡度 i=1:2 的山坡 CF，点 C 与点 B 在同一水平面上，CF 与 AB 在同一平面内．某数学兴趣小组为了测量楼 AB 的高度，在坡底 C 处测得楼顶 A 的仰角为 45°，然后沿坡面 CF 上行了 20 5 米到达点 D 处，此时在 D 处测得楼顶 A 的仰角为 30°，求楼 AB 的高度． 26 / 30 解 ：在 Rt△DEC 中 ，∵ i=DE∶DC=1∶2，且 DE2+EC2=DC2.∴DE2+（2DE）2=（ 20 5 ）2.解得：DE=20m， EC=40m.过点 D 作 DG⊥AB 于点 G，过 点 C 作 CH⊥DG 于点 H，则四边形 DEBG、DECH、BCHG 都是矩形.∵∠ACB=45°，AB⊥BC，∴ AB=BC，设 AB=BC=xm，则 AG=（x-20）m，DG=（x+40） m，在 Rt△ADG 中，∵ AG DG =tan∠ADG，∴ 20 3 40 3 x x − =+ ，解得：x=50+30 3 .答：楼 AB 的高度 为（50+30 3 ）米. 17.（2019·达州）渠县賨人谷是国家 AAAA级旅游景区，以“奇山奇水奇石景，古賨古洞古部落”享 誉巴渠，被誉为川东“小九寨”，蹲坐着观音崖一块奇石是一只“哮天犬”，昂首向天，望穿古今. 一个周末，某数学兴趣小组的几名同学想测出“哮天犬”上嘴尖与头顶的距离，他们把蹲着的“哮 天 犬”抽象成 ABCD，想法测出了尾部 C 看头顶 B 的仰角为 40°，从前脚落地点 D看上嘴尖 A 的 仰角刚好60°，CB=5米，CD=2.7米，景区管理员告诉同学们，上嘴尖到地面的距离是 3米，他们 很快就算出了 AB的长，你也算算？（结果精确到 0.1米，参考数据：sin40°≈0.64，cos40°≈0.77， tan40°≈0.84. 2 ≈1.41 3 ≈1.73） 解：过点 B 作 BF⊥CE 于点 F，再过点 A 作 AG⊥BF 于点 G，则四边形 AEFG 是矩形. 在 Rt△ADE 中，tan60° DE AE= AE=3， 33 = DE ，∴DE= 3 . 27 / 30 在 Rt△CBF 中，sin40° 64.0= BC BF ，CB=5， ∴BF≈3.2，cos40°= BC CF ≈0.77 ， CB=5，∴CF≈3.85. ∵CD=2.7 ，∴EF=CD+DE-CF≈0.58 ，BG=BF-AE≈0.2， ∴AB= 22 BGAG + ≈0.6m. 18.(2019·巴中)某区域平面示意图如图所示,点 D 在河的右侧,红军路 AB 与某桥 BC 互相垂直.某校”数 学兴趣小组”在”研学旅行”活动中,在 C 处测点 D 位于西北方向,又在 A 处测得点 D 位于南偏东 65°方 向,另测得 BC＝414m,AB＝300m,求出点D到AB的距离.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈ 2.14) 解：过点 D 作 DE⊥AB 于点 E,作 DF⊥BC 于点 F, ∵AB⊥BC,∴四边形 DEBF 是矩形,DE＝BF,EB＝DF, 在 Rt△AED 中,AE＝ tan 65 ED  ,∴BE＝AB－AE＝300－ tan 65 ED  , ∴DF＝BE＝300－ tan 65 ED  , 在 Rt△CDF 中,∠DCF＝45°, ∴∠FDC＝∠FCD, ∴CF＝DF＝300－ tan 65 ED  , ∴BC＝BF+FC＝300－ tan 65 ED  +ED, ∵BC＝414, ∴300－ tan 65 ED  +ED＝414, ∴ED＝214, ∴点 D 到 AB 的距离为 214m. 19.（2019·潍坊）自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多．为方便群众步行健 28 / 30 身，某地政府决定对一段如图 1 所示的坡路进行改造．如图 2 所示，改造前的斜坡 AB=200 米，坡度为 1∶ 3 ；将斜坡 AB 的高度 AE 降低 AC=20 米后，斜坡 AB 改造为斜坡 CD，其坡度为 1∶4．求斜坡 CD 的长．（结果保留根号） 解：在 Rt△ABE 中，∵tan∠ABE=1∶ 3 ， ∴∠ABE=30°． ∵AB=200， ∴AE= 1 2 AB=100． ∵AC=20， ∴CE=100－20=80． 在 Rt△CDE 中， ∵tanD=1∶4， ∴sinD= 17 17 ． ∴ 17 17 CE CD = ． ∴CD=80 17 （米） 答：斜坡 CD 的长是80 17 米． 20.(2019·聊城)某数学兴趣小组要测量实验大楼部分楼体的高度(如图①所示,CD 部分),在起点 A 处测 得 大楼部分楼体 CD 的顶端 C 点的仰角为 45°,底端 D 点的仰角为 30°,在同一剖面沿水平地面向前走 20 米到达 B 处,测得顶端 C 的仰角为 63.4°(如图②所示),求大楼部分楼体 CD 的高度约为多少米?(精确 到 1 米) (参考数据:sin63.4°≈0.89,cos63.4°≈0.45,tan63.4°≈2.00, 2 ≈1.41, 2 ≈1.73) 29 / 30 解：设楼高 CE 为 x 米,∵在 Rt△AEC 中,∠CAE＝45°,∴AE＝CE＝x,∵AB＝20,∴BE＝x－20,在 Rt△ CEB 中,CE＝BEtan63.4°≈2(x－20),∴2(x－20)＝x,解得 x＝40,在 Rt△DAE 中,DE＝AEtan30°＝ 40 3 3 , ∴CD＝CE－DE＝40－ 40 3 3 ≈17(米).答:大楼部分楼体 CD 的高度约为 17 米. 21.（2019·岳阳）慈氏塔位于岳阳市城西洞庭湖边，是湖南省保存最好的古塔建筑之一．如图，小亮 的 目高 CD 为 1.7 米，他站在 D 处测得塔顶的仰角∠ACG 为 45°，小琴的目高 EF 为 1.5 米，她站在 距离 塔底中心 B 点 a 米远的 F 处，测得塔顶的仰角∠AEH 为 62.3°．（点 D、B、F 在同一水平线 上，参考 数据：sin62.3°≈0.89，cos62.3°≈0.46，tan62.3°≈1.9） （1）求小亮与塔底中心的距离 BD；（用含 a 的式子表示） （2）若小亮与小琴相距 52 米，求慈氏塔的高度 AB． 解：（1）在 Rt△AEH 中，∠AEH=62.3°， tan 62.3 AH EH °= ． ∴AH=EH·tan62.3°=BF·tan62.3°=1.9a． ∵GH=GB－HB=CD－EF=1.7－1.5=0.2， ∴AG=AH－GH=1.9a－0.2． 在 Rt△ACG 中， ∵∠ACG=45°， 30 / 30 ∴CG=AG=1.9a－0.2． ∴BD=CG=1.9a－0.2． 所以小亮与塔底中心的距离 BD 为（1.9a－0.2）米． （2）∵DF=BD+BF， ∴1.9a－0.2＋a=52． 解得：a=18 ∴AB=AH＋BH=1.9a＋1.5=1.9×18＋1.5=35.7（米）． 所以慈氏塔的高度 AB 为 35.7 米． 22.（2019·怀化）如图，为测量一段笔直自西向东的河流的河面宽度，小明在南岸 B 处测得对岸 A 处 一 棵柳树位于北偏东 60°方向，他以每秒 1.5 米的速度沿着河岸向东步行 40 秒后到达 C 处，此时测得 柳树 位于北偏东 30°方向，试计算此段河面的宽度. 解：过 A 点作 AD⊥BC，垂足为 D. 根据题意可得∠ABC=30°，∠ACD=60°，BC=40×1.5=60 米， 在 Rt△ABD 中，BD= tan 30 AD  = 3 AD， 在 Rt△ACD 中，CD= tan 60 AD  = 3 3 AD， ∴BC=BD-CD= 23 3 AD=60， ∴AD=30 3 . 所以此段河面的宽度为 30 3 .