- 2021-11-12 发布 |
- 37.5 KB |
- 12页


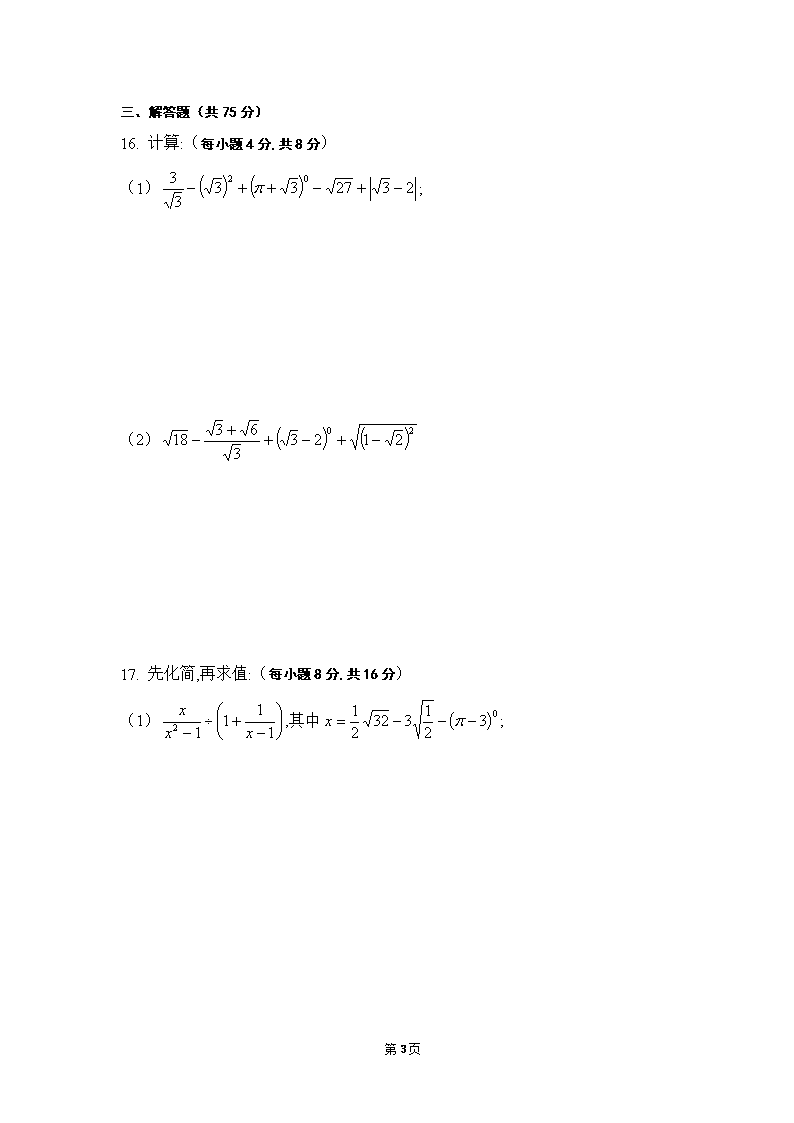
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华东师大版 九年级上册 第21章 二次根式单元测试卷
第21章 二次根式单元测试卷 姓名____________ 时间: 90分钟 满分:120分 总分____________ 一、选择题(每小题3分,共30分) 1. 若式子在实数范围内有意义,则的取值范围是 【 】 (A) (B)≤1 (C) (D)≥1 2. 如果成立,则实数的取值范围是 【 】 (A)≤0 (B)≤3 (C)≥ (D)≥3 3. 已知是△ABC的三边,化简 【 】 (A) (B) (C) (D) 4. 下列计算中正确的是 【 】 (A) (B) (C) (D) 5. 计算:的结果是 【 】 (A) (B) (C) (D) 6. 已知,且,则的值是 【 】 (A) (B) (C) (D)不能确定 7. 把根号外的因式移到根号内结果为 【 】 (A) (B) (C) (D) 8. 如果为有理数,那么等于 【 】 (A)2 (B)3 (C)8 (D)10 第12页 9. 对于任意的正数定义运算※为:※,计算(3※2)(8※12)的结果为 【 】 (A) (B)2 (C) (D)20 10. 已知为正整数,化简的结果是 【 】 (A) (B) (C) (D) 或选作下题: 设,则与最接近的数是 【 】 (A)2017 (B)2018 (C)2019 (D)2020 二、填空题(每小题3分,共15分) 11. 无论取任何实数,都有意义,则的取值范围是__________. 12. 若实数满足,则的值是_________. 13. 计算:_________. 14. 设,已知,则代数式的值是_________(用表示). 15. 观察下列等式:……,请你从上述等式中找出规律,并利用这一规律计算: _________. 第12页 三、解答题(共75分) 16. 计算:(每小题4分,共8分) (1); (2) 17. 先化简,再求值:(每小题8分,共16分) (1),其中; 第12页 (2),其中. 18. (10分)若,求的值. 19. (10分)已知,求的值. 第12页 20. (10分)已知,,试比较与的大小. 21. (10分)阅读材料: 黑白双雄,纵横江湖;双剑合璧,天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的“对子”.如:,,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式的除法可以这样解:如,.像这样把分母中的根号化去,叫作分母有理化. 解决问题: (1)的有理化因式是__________;将分母有理化得_________; (2)已知,则_________; (3)计算:①; ②; 第12页 (4)已知,则三者的大小关系为__________. 22. (11分) 设为自然数,如果成立,求的值. 第12页 第21章 二次根式单元测试卷参考答案 一、选择题(每小题3分,共30分) 题号 1 2 3 4 5 答案 C B C B B 题号 6 7 8 9 10 或 答案 B C D B C B 二、填空题(每小题3分,共15分) 11. ≥9 12. 13. 14. 15. 2016 第12页 三、解答题(共75分) 16. 计算:(每小题4分,共8分) (1) 解:原式 (2) 解:原式 17. 先化简,再求值:(每小题8分,共16分) (1),其中; 解: ……………………………4分 …………………………6分 当时 原式. ……………………………………8分 第12页 (2),其中. 解: …………………………5分 当时 原式 …………………………7分 ……………………………………8分 18. (10分) 解:∵≥0,≥0 ∴≥0,≥0 ∴≥150,≤150 ∴ ……………………………………3分 ∴ ……………………………………4分 ∵≥0,≥0 ∴ ……………………………………6分 解之得: ……………………………………9分 ∴. ……………………………………10分 19. (10分)已知,求的值. 分析:一般情况下,像这样的双重二次根式,其被开放数必为完全平方数(式). 解:∵ ∴ ……………………………………4分 ……………………………………8分 第12页 当时 原式 ……………………………………10分 结论:对于二次根式,若是完全平方数,则也是完全平方数. 20. (10分)已知, ,试比较与的大小. 解:∵ ∴ ……………………………………6分 ∵ ∴ ……………………………………8分 ∴ ∴…………………………10分 21. (10分)阅读材料: 解:(1); ; ……………………………………2分 (2)98; ……………………………………4分 解析:∵ ∴ ∴ ∴ (3)①解:原式 ; ……………………………………6分 ②2009;(过程略) ……………………………………8分 (4). ……………………………………10分 第12页 解析:∵ ∴ ∵∴ ∴. 22. (11分) 设为自然数,如果成立,求的值. 解:∵ ∴ ∴ ……………………………………4分 ∵ ∴ ∴ ∴或 解之得: ……………………………………10分 ∵为自然数 ∴. ……………………………………11分 部分选择题、填空题答案解析 6. 已知,且,则的值是 【 】 (A) (B) (C) (D)不能确定 解析:∵ ∴ 第12页 ∴ ∵ ∴ ∴ 答案选择【 B 】. 重要结论: 若,则;若,则. 10. 已知为正整数,化简的结果是 【 】 (A) (B) (C) (D) 解析:结论也是已知信息,由题目提供的四个备选答案可知:被开方式必为完全平方式. 我们可取,易知【 C 】正确.再一般化,此时目标明确. ∵为正整数 ∴原式 注意:. 答案选择【 C 】. 或选作下题: 设,则与最接近的数是 【 】 (A)2017 (B)2018 (C)2019 (D)2020 解析:由上面的解析可知,当时, 由结果可知,与最接近的数是2018. 答案选择【 B 】. 11. 无论取任何实数,都有意义,则的取值范围是__________. 解析:本题的意思即:无论取任何实数,被开方数均为非负数. ∵≥0 第12页 ∴当≥0,即≥9时 ≥0 也即≥0. 12. 若实数满足 , 则的值是_________. 解析: ∵≥0, ≥0 ∴ ∴ ∴ 14. 设,已知,则代数式的值是_________(用表示). 解析:因为 所以 . 第12页查看更多