2009年北京市石景山区中考数学二模试卷

2009年北京市石景山区中考数学二模试卷

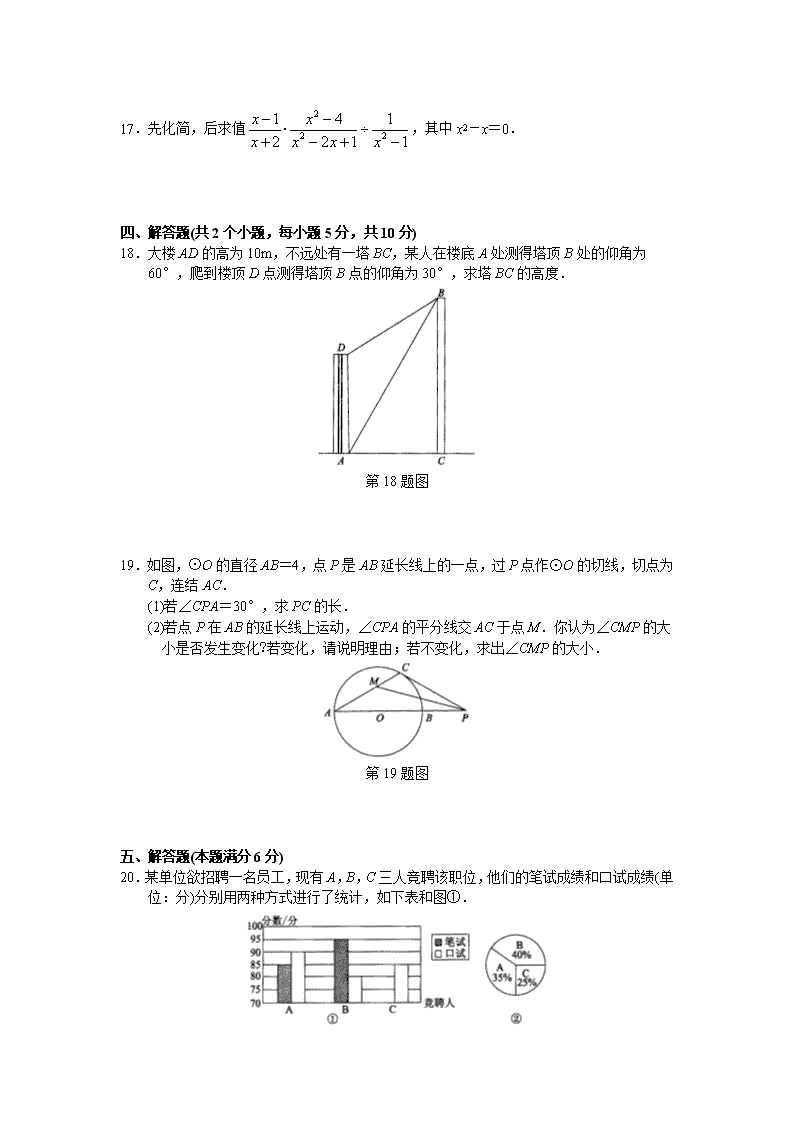
‎15 2009年北京市石景山区中考数学二模试卷 一、选择题(共8个小题，每小题4分，共32分)‎ 在每个小题给出的四个备选答案中，只有一个是正确的．‎ ‎1．｜－3｜的相反数是( )‎ A．－3 B．‎3 ‎C． D．±3‎ ‎2．下图中所示的几何体的主视图是( )‎ ‎3．明代长城究竟有多长?‎2009年4月18日，国家文物局和国家测绘局联合发布数据，明长城长度为‎8851.8km，比十年前最近的一次调查又增加了约‎2200km．‎8851.8km用科学记数法可以表示为(保留三个有效数字)( )‎ A．8.85×‎103m B．8.85×‎‎106m C．8.852×‎103m D．8.852×‎‎106m ‎4．若0＜a＜1，则下列四个不等式中正确的是( )‎ A． B． C． D．‎ ‎5．对于二次函数y＝ax2＋bx＋c(a≠0)，我们把使函数值等于0的实数x叫做这个函数的零点，则二次函数y＝x2－mx＋m－2(m为实数)的零点的个数是( )‎ A．1 B．‎2 ‎C．0 D．随m值变化 ‎6．小明外出游玩，带上棕色、蓝色、淡黄色3件上衣和蓝色、白色2条长裤，他任意拿出1件上衣和1条长裤正好是棕色上衣和蓝色长裤的概率是( )‎ A． B． C． D．‎ ‎7．有一列数a1，a2，a3,…，an，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若a1＝2，则a2009为( )‎ A．2009 B．‎2 ‎C． D．－1‎ ‎8．如图，在图①所示的正方形铁皮上剪下一个圆形和扇形，使之恰好围成图②所示的一个圆锥模型．设圆的半径为r，扇形的半径为R，则圆的半径与扇形的半径之间的关系为( )‎ A．R＝2r B． C．R＝3r D．R＝4r 第8题图 二、填空题(共4个小题，每小题4分，共16分)‎ ‎9．分解因式：‎2a2－8b2＝________．‎ ‎10．若，则mn＝________．‎ ‎11．如图，P为菱形ABCD的对角线AC上一点，PE⊥AB于E，PF⊥AD于F，PF＝3，则PE的长是________．‎ 第11题图 ‎12．观察下列有序数对：(3，－1)，(－5，)，(7，－)，(－9，)，…，根据你发现的规律，第100个有序数对是________．‎ 三、解答题(共5个小题，每小题5分，共25分)‎ ‎13．计算．‎ ‎14．解方程：3x(x＋2)＝5(x＋2)．‎ ‎15．反比例函数的图象在第一象限的分支上有一点A(2，3)，P为x轴正半轴上的一个动点．‎ ‎(1)求反比例函数的解析式．‎ ‎(2)当P在什么位置时，△OPA为直角三角形?求出此时P点的坐标．‎ ‎16．已知：如图，CD⊥AB于点D，BE⊥AC于点E，BE、CD交于点O，且AO平分∠BAC．‎ 求证：OB＝OC．‎ 第16题图 ‎17．先化简，后求值，其中x2－x＝0．‎ 四、解答题(共2个小题，每小题5分，共10分)‎ ‎18．大楼AD的高为‎10m，不远处有一塔BC，某人在楼底A处测得塔顶B处的仰角为 ‎60°，爬到楼顶D点测得塔顶B点的仰角为30°，求塔BC的高度．‎ 第18题图 ‎19．如图，⊙O的直径AB＝4，点P是AB延长线上的一点，过P点作⊙O的切线，切点为C，连结AC．‎ ‎(1)若∠CPA＝30°，求PC的长．‎ ‎(2)若点P在AB的延长线上运动，∠CPA的平分线交AC于点M．你认为∠CMP的大 小是否发生变化?若变化，请说明理由；若不变化，求出∠CMP的大小．‎ 第19题图 五、解答题(本题满分6分)‎ ‎20．某单位欲招聘一名员工，现有A，B，C三人竞聘该职位，他们的笔试成绩和口试成绩(单位：分)分别用两种方式进行了统计，如下表和图①．‎ 第20题图 A B C 笔试 ‎85‎ ‎95‎ ‎90‎ 口试 ‎80‎ ‎85‎ ‎(1)请将上表和图①中的空缺部分补充完整；‎ ‎(2)竞聘的最后一个程序是由该单位的300名职工进行投票，三位竞聘者的得票情况如图②(没有弃权票，每名职工只能推荐一个)，请计算每人的得票数；‎ ‎(3)若每票计1分，该单位将笔试、口试、得票三项测试得分按4∶3∶3的比例确定个人成绩，请计算三位竞聘者的最后成绩，并根据成绩判断谁能竞聘成功．‎ 六、解答题(共2个小题，第21题6分，第22题3分，共9分)‎ ‎21．汽车在行驶中，由于惯性作用，刹车后，还要向前滑行一段距离才能停住，我们称这段距离为“刹车距离”，刹车距离是分析事故的一个重要因素．在一个限速‎40km／h的弯道上，甲、乙两车相向而行，发现情况不对后同时刹车，但还是相碰了．事后现场测得甲车的刹车距离为‎12m，乙车的刹车距离超过‎10m，但小于‎12m．查有关资料知，甲车的刹车距离y(m)与车速x(km／h)的关系为y＝0.1x＋0.01x2；乙车的刹车距离s(m)与车速x(km／h)的关系如上图所示．请你就两车的速度方面分析这起事故是谁的责任．‎ 第21题图 ‎22．如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．‎ ‎(1)在图①中以格点为顶点画一个面积为5的正方形；‎ ‎(2)在图②中以格点为顶点画一个三角形，使三角形三边长分别为3、4、5；‎ ‎(3)在图③中以格点为顶点画一个三角形，使三角形三边长分别为2、、．‎ 第22题图 七、解答题(本题满分7分)‎ ‎23．如图，四边形ABCD是菱形，点D的坐标是(0，)，以点C为顶点的抛物线y＝ax2＋bx＋c恰经过x轴上的点A、B．‎ ‎(1)求点C的坐标；‎ ‎(2)若抛物线向上平移后恰好经过点D，求平移后抛物线的解析式．‎ 第23题图 八、解答题(本题满分7分)‎ ‎24．如图，在平面直角坐标系中，O为坐标原点，△AOB为等边三角形，点A的坐标是(4，0)，点B在第一象限，AC是∠OAB的平分线，并且与y轴交于点E，点M为直线AC上一个动点，把△AOM绕点A顺时针旋转，使边AO与边AB重合，得到△ABD．‎ ‎(1)求直线OB的解析式．‎ ‎(2)当M与点E重合时，求此时点D的坐标．‎ ‎(3)是否存在点M，使△OMD的面积等于3?若存在，求出点M的坐标；若不存在，请说明理由．‎ 第24题图 九、解答题(本题满分8分)‎ ‎25．(1)如图①，四边形ABCD中，AB＝CB，∠ABC＝60°，∠ADC＝120°，请你猜想线段DA、DC之和与线段BD的数量关系，并证明你的结论；‎ ‎(2)如图②，四边形ABCD中，AB＝BC，∠ABC＝60°，若点P为四边形ABCD内一点，且∠APD＝120°，请你猜想线段PA、PD、PC之和与线段BD 的数量关系，并证明你的结论．‎ 第25题图 答 案 ‎15．2009年北京市石景山区中考数学二模试卷 一、选择题 ‎1. A 2．D 3．B 4．A 5．B 6．C 7．C 8．D 二、填空题 ‎9．2(a＋2b)(a－2b) 10．－6 11．3 12．‎ 三、解答题 ‎13．解：原式 ‎．‎ ‎14．解：原方程可化为3x2＋x－10＝0，‎ 解得，．‎ ‎15．解：(1)将A(2，3)代入，得k＝6．‎ 所以函数解析式为．‎ ‎(2)当∠OPA＝90°时，P(2，0)．‎ 当∠OAP＝90°时，过A作AH⊥x轴于H，‎ 由△OAH∽△APH，‎ 得．即．‎ 所以，．‎ 此时，点P的坐标为．‎ ‎16．证明：∵CD⊥AB，BE⊥AC，‎ ‎∴∠ODA＝∠OEA．‎ ‎∵OA平分∠BAC，‎ ‎∴∠BAO＝∠CAO．‎ 又OA＝OA，‎ ‎∴△OAD≌△OAE．‎ ‎∴OD＝OE．‎ 在△OBD和△OCE中，‎ OD＝OE，∠ODB＝∠OEC，∠BOD＝∠COE，‎ ‎∴△OBD≌△OCE．‎ ‎∴OB＝OC．‎ ‎17．解：‎ ‎＝x2－x－2．‎ 当x2－x＝0时，‎ 原式＝－2．‎ 四、解答题 ‎18．解：过点B作BE⊥AD交AD延长线于点E．‎ 在Rt△BED中，由题意∠BDE＝60°．‎ 设DE＝x，则BE＝x．‎ 在Rt△BEA中，由题意∠BAE＝30°．‎ BE＝x，则AE＝3x．‎ ‎∴AD＝AE－DE＝3x－x＝2x＝10．‎ ‎∴x＝5．‎ ‎∴BC＝AD＋DE＝10＋5＝15．‎ 答：塔BC的高度为‎15m．‎ 第18题答图 ‎19．解：(1)连结OC，则OC⊥PC．‎ 在Rt△OCP中，，∠CPA＝30°．‎ ‎∴PC＝OC＝2.‎ ‎(2)∠CMP的大小不发生变化．‎ ‎∠CMP＝∠A＋∠MPA ‎．‎ 第19题答图 五、解答题 ‎20．解：(1)90 补充后的图如下：‎ 第20题答图 ‎(2)A：300×35％＝105 B：300×40％＝‎120 ‎‎ C：300×25％＝75‎ ‎(3)(分)‎ ‎(分)‎ ‎(分)‎ 所以，B能竞聘成功．‎ 六、解答题 ‎21．解：∵y＝0.1x＋0.01x2，而y＝12，‎ ‎∴0.1x＋0.01x2＝12．解之，得x1＝－40，x2＝30．‎ 舍去x＝－40，得x＝30＜40，所以甲车未超速行驶．‎ 设s＝kx，把(60，15)代入，得15＝60k．解得．故．‎ 由题意知．解得40＜x＜48．‎ 所以乙车超速行驶．‎ 综上所述，这次事故责任在乙方．‎ ‎22．解：如图所示，每问1分，共3分．‎ 第22题答图 七、解答题 ‎23．解：(1)连结AC，在菱形ABCD中，CD∥AB，‎ AB＝BC＝CD＝DA．‎ 由抛物线对称性可知AC＝BC．‎ ‎∴△ABC，△ACD都是等边三角形．‎ ‎．‎ ‎∴点C的坐标为(2，)．‎ ‎(2)由抛物线y＝ax2＋bx＋c的顶点为(2，)，‎ 可设抛物线的解析式为y＝a(x－2)2＋．‎ 由(1)可得A(1，0)，把A(1，0)代入上式，‎ 解得a＝－．‎ 设平移后抛物线的解析式为y＝－(x－2)2＋k，把(0，)代入上式得k＝5．‎ ‎∴平移后抛物线的解析式为y＝－(x－2)2＋5．‎ 即y＝－x2＋4x＋．‎ 第23题答图 八、解答题 ‎24．解：(1)B(2，6) lOB：y＝x．‎ ‎(2)如图①，由题意DA⊥x轴，‎ ‎∠EAO＝∠BAD＝30°．‎ 此时，‎ 即点D(4，8)．‎ ‎ ‎ ‎① ② ③‎ 第24题答图 ‎(3)如图②、图③，过M作MN⊥x轴，设MN＝a，‎ 当M在x轴上方时，‎ 由∠OAM＝30°，∴MA＝‎2a，NA＝a．‎ ‎．‎ 解得a＝3．‎ 当M在x轴下方时，‎ 由∠NAM＝30°，∴MA＝‎2a，NA＝a．‎ ‎．‎ 解得a＝1．‎ ‎∴M1(，3)，M2(5,－1)．‎ 九、解答题 ‎25．解：(1)如图①，延长CD至E，使DE＝DA．‎ 可证明△EAD是等边三角形．‎ 连结AC，可证明△BAD≌△CAE．‎ 故AD＋CD＝DE＋CD＝CE＝BD．‎ ‎ ‎ ‎① ②‎ 第25题答图 ‎(2)如图②，在四边形ABCD外侧作正三角形AD，‎ 可证明△AC≌△ADB，得C＝DB．‎ ‎∵四边形ADP符合(1)中条件，‎ ‎∴P＝AP＋PD．‎ 连结C，‎ ‎(i)若满足题中条件的点P在C上，‎ 则C＝P＋PC．‎ ‎∴C＝AP＋PD＋PC．‎ ‎∴BD＝PA＋PD＋PC．‎ ‎(ii)若满足题中条件的点P不在C上，‎ ‎∵C＜PB＋PC，‎ ‎∴C＜AP＋PD＋PC．‎ ‎∴BD＜PA＋PD＋PC．‎ 综上，BD≤PA＋PD＋PC．‎