鄂尔多斯专版2020中考数学复习方案第三单元函数及其图象第12课时二次函数的图象与性质课件

鄂尔多斯专版2020中考数学复习方案第三单元函数及其图象第12课时二次函数的图象与性质课件

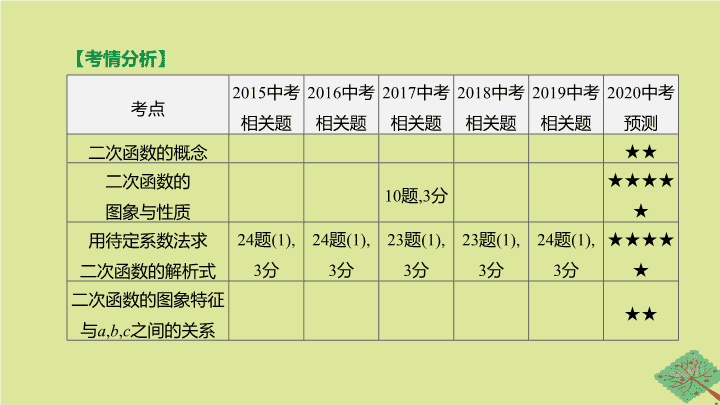
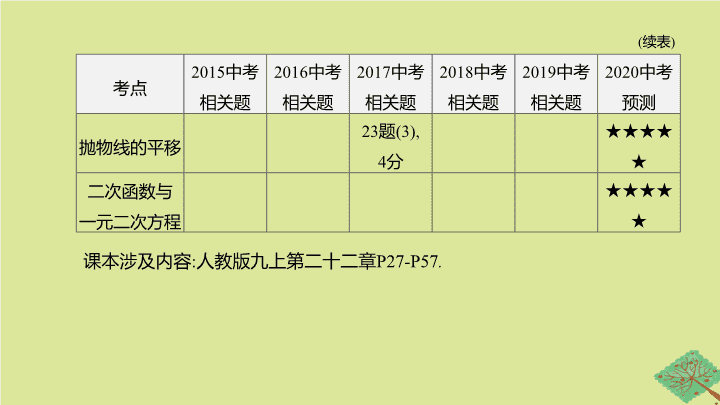
第 12 课时 二次函数的图象与性质 第三单元　函数及其图象 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考预测 二次函数的概念 ★★ 二次函数的 图象与性质 10 题 ,3 分 ★★★★★ 用待定系数法求 二次函数的解析式 24 题 (1), 3 分 24 题 (1), 3 分 23 题 (1), 3 分 23 题 (1), 3 分 24 题 (1), 3 分 ★★★★★ 二次函数的图象特征 与 a , b , c 之间的关系 ★★ ( 续表 ) 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考预测 抛物线的平移 23 题 (3), 4 分 ★★★★★ 二次函数与 一元二次方程 ★★★★★ 课本涉及内容 : 人教版九上第二十二章 P27 - P57 . 考点一　二次函数的概念 考点聚焦 一般地 , 形如 ① 　　 　　　　 ( a , b , c 是常数 , a ≠0) 的函数 , 叫做二次函数 .  【 温馨提示 】 函数 y = ax 2 + bx + c 未必是二次函数 , 当 ② 　　　　 时 , y = ax 2 + bx + c 是二次函数 .  y = ax 2 + bx + c a ≠0 考点二　二次函数的图象与性质 函数 　 y = ax 2 + bx + c ( a , b , c 为常数 , a ≠0) 　 a> 0 a< 0 图象 开口方向 开口 ③ 　　　　 , 并向上无限延伸   开口 ④ 　 　　 , 并向下无限延伸   对称轴 　 直线 ⑤ 　　 　   向下 向上 ( 续表 ) 函数 　 a> 0 a< 0 顶点坐标 　 ⑥ 　　　　　　   增减性 　 增大 减小 增大 减小 ( 续表 ) 函数 　 a> 0 a< 0 最值 　 二次 项系数 a 的特性 的大小决定抛物线的开口大小 , | a | 越大 , 抛物线的开口越小 ; | a | 越小 , 抛物线的开口越大 常数项 c 的 意义 c 是抛物线与 y 轴交点的纵坐标 , 即 x =0 时 , y = c 小 大 考点三　二次函数的图象与系数的关系 　　 项目 字母 　　 y = ax 2 + bx + c ( a , b , c 为常数 , a ≠0) 字母的符号 图象的特征 a a> 0 　 开口向 ⑬ 　 　   a< 0 　 开口向 ⑭ 　　　   b b= 0 　 对称轴为 ⑮ 　 　 轴   ab> 0( b 与 a 同号 ) 　 对称轴在 y 轴 ⑯ 　　 侧   ab< 0( b 与 a 异号 ) 　 对称轴在 y 轴 ⑰ 　 　 侧   上 下 y 左 右 ( 续表 ) 　　 项目 字母 　　 y = ax 2 + bx + c ( a , b , c 为常数 , a ≠0) 字母的符号 图象的特征 c c =0 　 经过点 ⑱ 　　　   c> 0 　 与 y 轴 ⑲ 　　 　 相交   c< 0 　 与 y 轴 ⑳ 　 　 　 相交   b 2 -4 ac b 2 -4 ac =0 　 与 x 轴有唯一交点 ( 顶点 ) b 2 -4 ac> 0 　 与 x 轴 有 ㉑ 　 　 个不同的交点   b 2 -4 ac< 0 　 与 x 轴没有交点 (0,0) 正半轴 负半轴 两 ( 续表 ) 　　 项目 字母 　　 y = ax 2 + bx + c ( a , b , c 为常数 , a ≠0) 字母的符号 特殊 关系 当 x =1 时 , y = a + b + c 当 x =-1 时 , y = ㉒ 　　 　   若 a + b + c> 0, 则当 x =1 时 , y> 0 若 a - b + c> 0, 则当 x = ㉓ 　 　 时 , y> 0  -1 a - b + c 考点四　二次函数图象的画法 考点五　二次函数的表示及解析式的求法 1 . 二次函数的三种表示方法 (1) 一般式 : ㉔ 　　　　　　　　　 .  (2) 顶点式 : y = a ( x - h ) 2 + k ( a ≠0), 其中二次函数图象的顶点坐标是 ㉕ 　　　　 .  (3) 两点式 : y = a ( x - x 1 )( x - x 2 )( a ≠0), 其图象与 x 轴的交点的坐标为 ㉖ 　　　　 .  y = ax 2 + bx + c ( a ≠0) ( h , k ) ( x 1 ,0),( x 2 ,0) 2 . 二次函数解析式的确定 用待定系数法求二次函数的解析式时 , 注意解析式的设法 , 常见情况如下 : 条件 设法 顶点在原点 y = ax 2 ( a ≠0) 顶点在 y 轴上 y = ax 2 + c ( a ≠0, y 轴为对称轴 ) 顶点在 x 轴上 y = a ( x - h ) 2 ( a ≠0, 直线 x = h 是对称轴 ) 抛物线过原点 y = ax 2 + bx ( a ≠0) 顶点 ( h , k ) y = a ( x - h ) 2 + k ( a ≠0) 抛物线与 x 轴的 交点 为 ( x 1 ,0),( x 2 ,0) y = a ( x - x 1 )( x - x 2 )( a ≠0) 考点六　二次函数图象的平移 将抛物线 y = ax 2 + bx + c ( a ≠0) 用配方法化成 ㉗ 　　　　　　　　　 的形式 , 而任意抛物线 y = a ( x - h ) 2 + k 均可由抛物线 y = ax 2 平移得到 , 具体平移方法如图 12-1:  图 12-1 y = a ( x - h ) 2 + k ( a ≠0) 【 温馨提示 】 确定抛物线平移后的解析式时最好利用顶点式 , 利用顶点的平移来研究图形的平移 . 考点七　二次函数与一元二次方程、不等式的关系 1 . 二次函数与一元二次方程的关系 抛物线 y = ax 2 + bx + c 与 x 轴 的交点个数 判别式 b 2 -4 ac 的正负 方程 ax 2 + bx + c =0 的实数根个数 2 个 b 2 -4 ac> 0 两 个 ㉘ 　 　　 的实数根   1 个 b 2 -4 ac =0 两 个 ㉙ 　 　　 的实数根   没有 b 2 -4 ac< 0 ㉚ 　　　　 实数根   没有 相等 不相等 2 . 二次函数与不等式的关系 (1) ax 2 + bx + c> 0 的解集 函数 y = ax 2 + bx + c 的图象位于 x 轴上方的部分对应的点的横坐标的取值范围 . (2) ax 2 + bx + c< 0 的解集 函数 y = ax 2 + bx + c 的图象位于 ㉛ 　　 　　 的部分对应的点的横坐标的取值范围 . x 轴下方 题组一　必会题 对点演练 1 . [2018· 岳阳 ] 抛物线 y =3( x -2) 2 +5 的顶点坐标是 ( 　　 ) A . (-2,5) B . (-2,-5) C . (2,5) D . (2,-5) 2 . [2019· 重庆 B 卷 ] 抛物线 y =-3 x 2 +6 x +2 的对称轴是 ( 　　 ) A . 直线 x =2 B . 直线 x =-2 C . 直线 x =1 D . 直线 x =-1 C C 3 . [2019· 雅安 ] 在平面直角坐标系中 , 对于二次函数 y =( x -2) 2 +1, 下列说法中错误的是 ( 　　 ) A .y 的最小值为 1 B . 图象顶点坐标为 (2,1), 对称轴为直线 x =2 C . 当 x< 2 时 , y 的值随 x 值的增大而增大 , 当 x ≥2 时 , y 的值随 x 值的增大而减小 D . 它的图象可以由 y = x 2 的图象向右平移 2 个单位长度 , 再向上平移 1 个单位长度得到 C 4 . [2019· 荆门 ] 抛物线 y =- x 2 +4 x -4 与坐标轴的交点个数为 ( 　　 ) A . 0 B . 1 C . 2 D . 3 [ 答案 ] C 　 [ 解析 ] 当 x =0 时 , y =- x 2 +4 x -4=-4, 则抛物线与 y 轴的交点坐标为 (0,-4), 当 y =0 时 ,- x 2 +4 x -4=0, 解得 x 1 = x 2 =2, 抛物线与 x 轴的交点坐标为 (2,0) . 所以抛物线与坐标轴有 2 个交点 . 故选 C . 5 . [2019· 呼和浩特 ] 二次函数 y = ax 2 与一次函数 y = ax + a 在同一坐标系中的大致图象可能是 ( 　　 ) D 图 12-2 题组二　易错题 【 失分点 】 考虑二次函数的增减性时 , 要关注自变量的取值及对称轴的位置 , 因为二次函数的增减性是分区域的 . 6 . [2019· 温州 ] 已知二次函数 y = x 2 -4 x +2, 关于该函数在 -1≤ x ≤3 的取值范围内 , 下列说法正确的是 ( 　　 ) A . 有最大值 -1, 有最小值 -2 B . 有最大值 0, 有最小值 -1 C . 有最大值 7, 有最小值 -1 D . 有最大值 7, 有最小值 -2 [ 答案 ] D 　 [ 解析 ] ∵二次函数 y = x 2 -4 x +2=( x -2) 2 -2, ∴该函数在 -1≤ x ≤3 的取值范围内 , 当 x =2 时 , y 有最小值 -2; 当 x =-1 时 , y 有最大值 7 . 故选 D . 7 . [2018· 潍坊 ] 已知二次函数 y =-( x - h ) 2 ( h 为常数 ), 当自变量 x 的值满足 2≤ x ≤5 时 , 与其对应的函数值 y 的最大值为 -1, 则 h 的值为 ( 　　 ) A . 3 或 6 B . 1 或 6 C . 1 或 3 D . 4 或 6 [ 答案 ] B 　 [ 解析 ] 二次函数 y =-( x - h ) 2 , 当 x = h 时 , 有最大值 0, 而当自变量 x 的值满足 2≤ x ≤5 时 , 与其对应的函数值 y 的最大值为 -1, 故 h< 2 或 h> 5 . 当 h< 2,2≤ x ≤5 时 , y 随 x 的增大而减小 , 故当 x =2 时 , y 有最大值 , 此时 -(2- h ) 2 =-1, 解得 : h 1 =1, h 2 =3( 舍去 ), 此时 h =1; 当 h> 5,2≤ x ≤5 时 , y 随 x 的增大而增大 , 故当 x =5 时 , y 有最大值 , 此时 -(5- h ) 2 =-1, 解得 : h 1 =6, h 2 =4( 舍去 ), 此时 h =6 . 综上可知 h =1 或 6, 故选 B . 考向一　二次函数的图象及性质 解 :(1) 略 . 解 : (3) 当 x< 1 时 , y 随 x 的增大而增大 ; 当 x ≥1 时 , y 随 x 的增大而减小 . 解 : (4) y 1 >y 2 >y 3 . | 考向精练 | 1 . [2019· 攀枝花 ] 在同一坐标系中 , 二次函数 y = ax 2 + bx 与一次函数 y = bx - a 的图象可能是 ( 　　 ) [ 答案 ] C 　 [ 解析 ] 据参数符号可排除 A 、 D 选项 , 联立两函数解析式所得方程无解 , 则两函数图象无交点 , 故选 C . 图 12 - 3 2 . [2019· 烟台 ] 已知二次函数 y = ax 2 + bx + c 的 y 与 x 的部分对应值如下表 : 下列结论 : ①抛物线的开口向上 ; ②抛物线的对称轴为直线 x =2; ③当 0 0; ④抛物线与 x 轴的两个交点间的距离是 4; ⑤若 A ( x 1 ,2), B ( x 2 ,3) 是抛物线上两点 , 则 x 1 x 2 , 所以结论⑤错误 . 3 . 已知二次函数 y =-( x -1) 2 +2, 当 t 1 时 , y 的值随 x 值的增大而减小 , 而 t 0; 开口向下 , 则 a< 0; ②根据对称轴的位置和 a 的符号判定 b 的符号 : 对称轴在 y 轴左侧 , 则 a , b 同号 ; 对称轴在 y 轴右侧 , 则 a , b 异号 ; ③由抛物线与 y 轴的交点判断 c 的符号 : 交点在 y 轴正半轴 , 则 c> 0; 交点在 y 轴负半轴 , 则 c< 0; ④根据 a , b , c 的符号判定 ab , bc , ac , abc 的符号 ; ⑤根据抛物线与 x 轴的交点个数判定 b 2 -4 ac 与 0 的大小关系 ; ⑥特殊等式的判断 : 见到 a + b + c ( 或 4 a +2 b + c ), 则令 x =1( 或 x =2), 看抛物线上对应点的纵坐标位置 ; 见到 a - b + c ( 或 4 a -2 b + c ), 则令 x =-1( 或 x =-2), 看抛物线上对应点的纵坐标的位置 , 根据位置判定其符号 . | 考向精练 | 1 . [2019· 巴中 ] 二次函数 y = ax 2 + bx + c ( a ≠0) 的图象如图 12-5 所示 , 下列结论 : ① b 2 > 4 ac , ② abc< 0, ③ 2 a + b - c> 0, ④ a + b + c< 0, 其中正确的是 ( 　　 ) A . ①④ B . ②④ C . ②③ D . ①②③④ 图 12-5 [ 答案 ] A 2 . [2019· 安顺 ] 如图 12-6, 已知二次函数 y = ax 2 + bx + c 的图象与 x 轴分别交于 A , B 两点 , 与 y 轴交于 C 点 , OA = OC , 由抛物线的特征写出如下结论 : ① abc> 0; ② 4 ac - b 2 > 0; ③ a - b + c> 0; ④ ac + b +1=0 . 其中正确的个数是 ( 　　 ) A . 4 个 B . 3 个 C . 2 个 D . 1 个 图 12-6 [ 答案 ] B 　 [ 解析 ] ①从图象中易知 a> 0, b< 0, c< 0, ∴ abc> 0, 故①正确 ; ②∵抛物线与 x 轴有两个交点 , ∴ b 2 -4 ac> 0, ∴ 4 ac - b 2 < 0, 故②错误 ; ③当 x =-1 时 y = a - b + c , 由图象知 (-1, a - b + c ) 在第二象限 , ∴ a - b + c> 0, 故③正确 . ④设 C (0, c ), 则 OC =| c |, ∵ OA = OC =| c |, ∴ A ( c ,0), 代入抛物线得 ac 2 + bc + c =0, 又 c ≠0, ∴ ac + b +1=0, 故④正确 . 考向三　求二次函数的解析式 例 3 根据下列条件求解析式 . (1) 抛物线 y = ax 2 + bx +2 的图象过 B (-2,6), C (2,2) 两点 , 试求抛物线的解析式 ; (2) 已知二次函数的图象以 A (-1,4) 为顶点 , 且过点 B (2,-5), 求二次函数的解析式 ; (3) 已知二次函数 y = ax 2 + bx + c 的图象经过 A (-1,0), B (3,0), C (0,-3) 三点 , 求这个二次函数的解析式 . ( 用两种方法 ) 例 3 根据下列条件求解析式 . (2) 已知二次函数的图象以 A (-1,4) 为顶点 , 且过点 B (2,-5), 求二次函数的解析式 ; 解 : (2) 由顶点 A (-1,4), 可设二次函数的解析式为 y = a ( x +1) 2 +4( a ≠0) . ∵二次函数的图象过点 B (2,-5), ∴ -5= a (2+1) 2 +4, 解得 a =-1 . ∴二次函数的解析式是 y =-( x +1) 2 +4, 即 y =- x 2 -2 x +3 . 例 3 根据下列条件求解析式 . (3) 已知二次函数 y = ax 2 + bx + c 的图象经过 A (-1,0), B (3,0), C (0,-3) 三点 , 求这个二次函数的解析式 . ( 用两种方法 ) 解 : (3)( 方法一 ) 这个二次函数的解析式为 y = a ( x +1)( x -3) . 把 (0,-3) 代入 , 得 a ×1×(-3)=-3, 解得 a =1 . ∴这个二次函数的解析式为 y =( x +1)( x -3)= x 2 -2 x -3 . | 考向精练 | (1) 已知二次函数的图象经过点 (-1,-5),(0,-4) 和 (1,1), 求这个二次函数的解析式 . (2) 已知抛物线的顶点坐标为 (2,-3), 与 y 轴交于点 (0,-1), 求这条抛物线的解析式 . (3) 抛物线与 x 轴交于点 (1,0) 和 (3,0), 且图象经过点 (0,3), 求抛物线的解析式 . (2) 已知抛物线的顶点坐标为 (2,-3), 与 y 轴交于点 (0,-1), 求这条抛物线的解析式 . (3) 抛物线与 x 轴交于点 (1,0) 和 (3,0), 且图象经过点 (0,3), 求抛物线的解析式 . 解 : ( 3 ) 设抛物线的解析式为 y = a ( x -1)( x -3), 将 (0,3) 代入 , 得 3= a (0-1)(0-3), 解得 a =1, ∴抛物线的解析式为 y =( x -1)( x -3)= x 2 -4 x +3 . y =2( x +1) 2 -2 考向四　二次函数图象的平移 例 4 [2019· 宜宾 ] 将抛物线 y =2 x 2 的图象先向左平移 1 个单位 , 再向下平移 2 个单位 , 所得图象的解析式为 　　 　　 .  | 考向精练 | 1 . [2019· 济宁 ] 将抛物线 y = x 2 -6 x +5 向上平移两个单位长度 , 再向右平移一个单位长度后 , 得到的抛物线解析式是 ( 　　 ) A .y =( x -4) 2 -6 B .y =( x -1) 2 -3 C .y =( x -2) 2 -2 D .y =( x -4) 2 -2 [ 答案 ] D 　 [ 解析 ] y = x 2 -6 x +5=( x -3) 2 -4, 把该抛物线向上平移两个单位长度 , 再向右平移一个单位长度后 , 得 y =( x -3-1) 2 -4+2, 即 y =( x -4) 2 -2 . 2 . [2019· 淄博 ] 将二次函数 y = x 2 -4 x + a 的图象向左平移一个单位 , 再向上平移一个单位 , 若得到的函数图象与直线 y =2 有两个交点 , 则 a 的取值范围是 ( 　　 ) A .a> 3 B .a< 3 C .a> 5 D .a< 5 [ 答案 ] D 　 [ 解析 ] ∵ y = x 2 -4 x + a =( x -2) 2 + a -4, 图象先向左平移一个单位 , 再向上平移一个单位后的解析式为 y =( x -1) 2 + a -3, 令 2=( x -1) 2 + a -3, 即 x 2 -2 x + a -4=0, 由 Δ =4-4( a -4) > 0, 得 a< 5 .