- 2021-11-11 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学上册 第4章 相似三角形 4
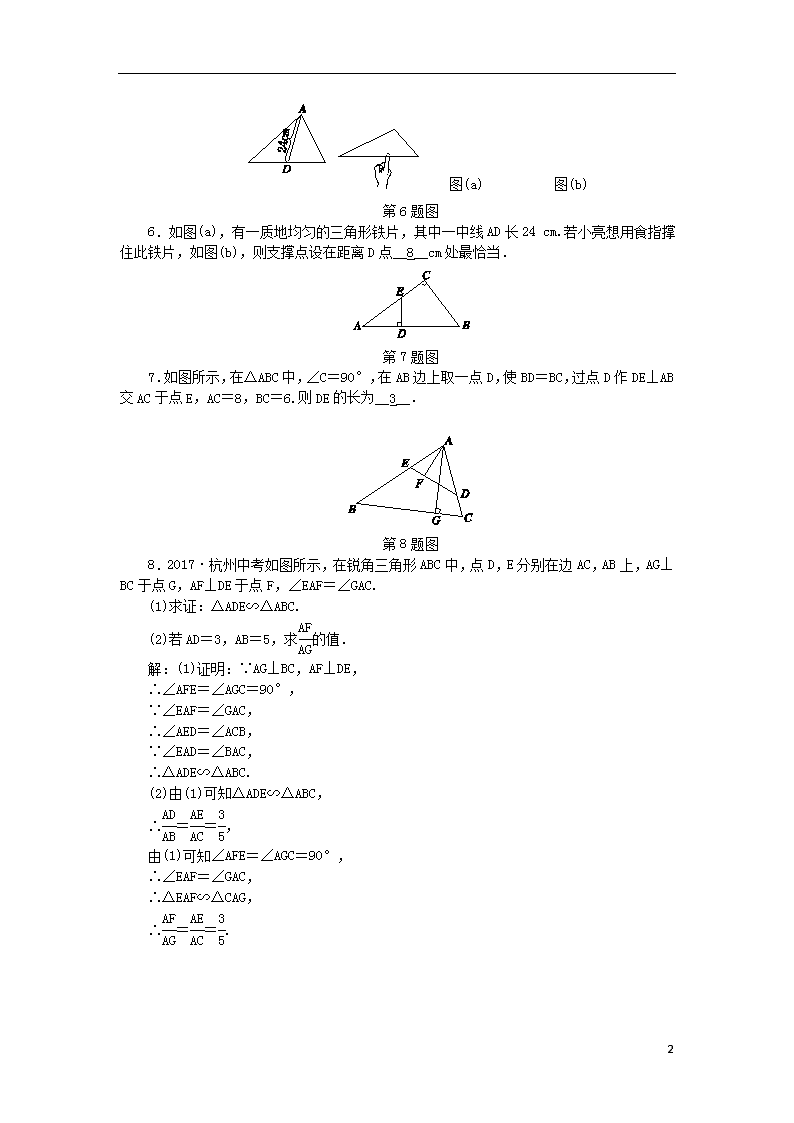
4.5 相似三角形的性质及其应用(1) (见A本45页) A 练就好基础 基础达标 1.用幻灯机将一个三角形ABC的边长放大到原来的4倍,下列说法中不正确的是( A ) A.放大后∠A,∠B,∠C是原来的4倍 B.放大后对应角平分线是原来的4倍 C.放大后对应边长是原来的4倍 D.放大后对应中线长是原来的4倍 2.兰州中考已知△ABC∽△DEF,若△ABC与△DEF的相似比为,则△ABC与△DEF对应中线的比为( A ) A. B. C. D. 3.设O为△ABC内部一点,且满足S△OAB=S△OBC=S△OAC,则O为△ABC的( B ) A.外心 B.重心 C.垂心 D.任意一点 第4题图 4.安徽中考如图所示,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( B ) A.4 B.4 C.6 D.4 5.如图所示,△ABC中的AC边与一刻度尺重叠放置,DE∥AB,若DE=30,则AB=__45__. 第5题图 5 图(a) 图(b) 第6题图 6.如图(a),有一质地均匀的三角形铁片,其中一中线AD长24 cm.若小亮想用食指撑住此铁片,如图(b),则支撑点设在距离D点__8__cm处最恰当. 第7题图 7.如图所示,在△ABC中,∠C=90°,在AB边上取一点D,使BD=BC,过点D作DE⊥AB交AC于点E,AC=8,BC=6.则DE的长为__3__. 第8题图 8.2017·杭州中考如图所示,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC. (1)求证:△ADE∽△ABC. (2)若AD=3,AB=5,求的值. 解:(1)证明:∵AG⊥BC,AF⊥DE, ∴∠AFE=∠AGC=90°, ∵∠EAF=∠GAC, ∴∠AED=∠ACB, ∵∠EAD=∠BAC, ∴△ADE∽△ABC. (2)由(1)可知△ADE∽△ABC, ∴==, 由(1)可知∠AFE=∠AGC=90°, ∴∠EAF=∠GAC, ∴△EAF∽△CAG, ∴==. 5 第9题图 9.如图所示,在△ABC中,AD平分∠BAC,按如下步骤作图: 第一步,分别以点A,D为圆心、大于AD长的一半为半径作弧,在AD两侧交于点M,N; 第二步,连结MN分别交AB,AC于点E,F; 第三步,连结DE,DF. 若BD=6,AF=4,CD=3,求BE的长. 解:∵根据作法可知,MN是线段AD的垂直平分线, ∴AE=DE,AF=DF,∴∠EAD=∠EDA, ∵AD平分∠BAC,∴∠BAD=∠CAD, ∴∠EDA=∠CAD,∴DE∥AC,同理,DF∥AE, ∴四边形AEDF是菱形,∴AE=DE=DF=AF, ∵AF=4,∴AE=DE=DF=AF=4, ∵DE∥AC,∴=, ∵BD=6,AE=4,CD=3,∴=,∴BE=8. B 更上一层楼 能力提升 第10题图 10.如图所示,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,转动三角板使两直角边始终与BC,AB相交,交点分别为M,N. 如果AB=4,AD=6,OM=x,ON=y,则y与x的表达式是( D ) A.y=x B.y= C.y=x D.y=x 11.滨州中考如图所示,在矩形ABCD中,AB=,BC=,点E在对角线BD上,且BE=1.8,连结AE并延长交DC于点F,则=____. 第11题图 5 12.已知直角三角形的两条直角边分别为3 cm、4 cm,则重心到外心的距离为____cm. 13.2017·泸州中考在△ABC中,已知BD和CE分别是边AC,AB上的中线,且BD⊥CE,垂足为O.若OD=2 cm,OE=4 cm,则线段AO的长度为__4__cm. 14.如图所示,△ABC是一张直角三角形彩色纸,AC=15 cm,BC=20 cm.若将斜边上的高CD 分成n等分,然后裁出(n-1)张宽度相等的长方形纸条.则这(n-1)张纸条的面积和是____cm2. 第14题图 C 开拓新思路 拓展创新 15.如图所示,在△ABC和△DEF中,∠A=∠D=90°,AB=DE=3,AC=2DF=4. (1)这两个三角形是否相似?请说明理由. (2)能否分别过点A,D在这两个三角形中各作一条辅助线,使△ABC分割成的两个三角形与△DEF分割成的两个三角形分别相似?证明你的结论. 第15题图 解:(1)不相似,理由如下: ∵在Rt△BAC中,∠A=90°,AB=3,AC=4; 在Rt△EDF中,∠D=90°,DE=3,DF=2. ∴=1,=2或=,=. ∴≠或≠. ∴Rt△BAC与Rt△EDF不相似. (2)能作如图所示的辅助线进行分割. 具体作法:作∠BAM=∠E,交BC于M;作∠NDE=∠B,交EF于N. 第15题答图 由作法和已知条件可知△BAM∽△DEN. ∵∠BAM=∠E,∠NDE=∠B, 5 又∵∠AMC=∠BAM+∠B,∠FND=∠E+∠NDE, ∴∠AMC=∠FND. ∵∠FDN=90°-∠NDE,∠C=90°-∠B, ∴∠FDN=∠C.∴△AMC∽△FND. 16.2017·河池中考(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M.求证:AE=BF. (2)如图2,将(1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论. 第16题图 证明:(1)∵四边形ABCD是正方形, ∴∠ABC=∠C,AB=BC. ∵AE⊥BF, ∴∠AMB=∠BAM+∠ABM=90°, ∵∠ABM+∠CBF=90°, ∴∠BAM=∠CBF. 在△ABE和△BCF中, ∴△ABE≌△BCF(ASA),∴AE=BF. (2)AE=BF. ∵四边形ABCD是矩形, ∴∠ABC=∠C,∵AE⊥BF, ∴∠AMB=∠BAM+∠ABM=90°, ∵∠ABM+∠CBF=90°, ∴∠BAM=∠CBF, ∴△ABE∽△BCF, ∴==, ∴AE=BF. 5查看更多