2020届九年级数学下册 第6章 二次函数 6

2020届九年级数学下册 第6章 二次函数 6

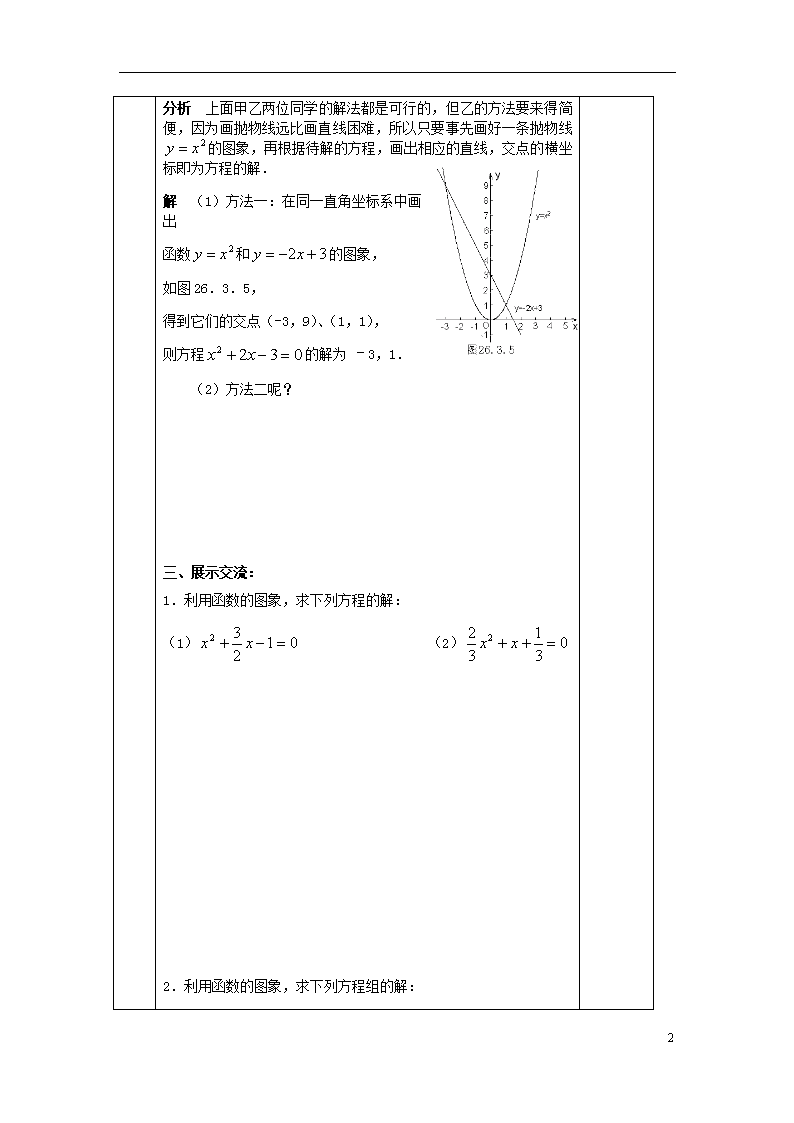
二次函数与一元二次方程 课题 ‎§6.3 二次函数与一元二次方程（2）‎ 自主空间 学习目标 知识与技能：掌握一元二次方程及二元二次方程组的图象解法．‎ 进一步体验数形结合的数学方法。‎ 学习重点 一元二次方程及二元二次方程组的图象解法 学习难点 一元二次方程及二元二次方程组的图象解法 教学流程 预 习 导 航 你能求方程的解，你是如何解决的呢？我们来看一看两位同学不同的方法．‎ 甲：将方程化为，画出的图象，观察它与x轴的交点，得出方程的解．‎ 乙：分别画出函数和的图象，观察它们的交点，把交点的横坐标作为方程的解．‎ 你对这两种解法有什么看法？请与你的同学交流．‎ 合 作 探 究 一、新知探究：‎ 你根据函数y=x2+2x-5 的图象，求出方程x2+2x-5=0的近似根吗？‎ 你能参照上面两位同学的方法试着去解决吗？‎ 二、例题分析：‎ 利用函数的图象，求方程的解：‎ 5‎ 分析 上面甲乙两位同学的解法都是可行的，但乙的方法要来得简便，因为画抛物线远比画直线困难，所以只要事先画好一条抛物线的图象，再根据待解的方程，画出相应的直线，交点的横坐标即为方程的解．‎ 解 （1）方法一：在同一直角坐标系中画出 函数和的图象，‎ 如图26．3．5，‎ 得到它们的交点（-3，9）、（1，1），‎ 则方程的解为 –3，1．‎ ‎（2）方法二呢？‎ 三、展示交流：‎ ‎1．利用函数的图象，求下列方程的解：‎ ‎（1） （2）‎ ‎2．利用函数的图象，求下列方程组的解：‎ 5‎ ‎（1）； （2）．‎ 四、提炼总结：一般地，求一元二次方程的近似解时，‎ 可先将方程化为，‎ 然后分别画出函数和的图象，得出交点，交点的横坐标即为方程的解．‎ 当 堂 达 标 ‎1．已知二次函数y=-x2+2x+m与x轴有两个交点，其中一个交点的横坐标x1的取值范围是3

查看更多