2020-2021学年沪科版九年级数学上册第22章、第23章测试题及答案解析（各一套）

2020-2021学年沪科版九年级数学上册第22章、第23章测试题及答案解析（各一套）

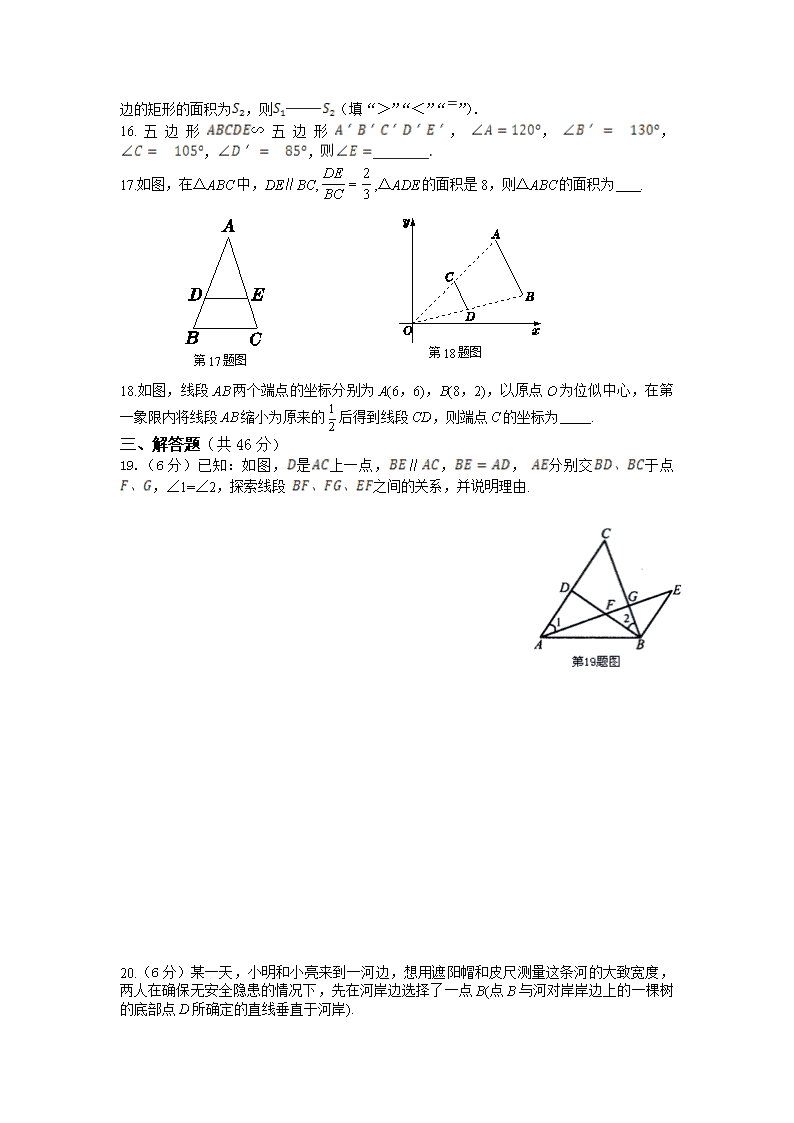
沪科版九年级数学上册第22章测试题 ‎（时间：90分钟 分值：100分）‎ 一、选择题（每小题3分，共30分）‎ ‎1.下列四组图形中，不是相似图形的是（ ）‎ A ‎ B ‎ C ‎ D ‎ ‎2.若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为（ ）‎ A.1∶2 B.2∶1‎ C.1∶4 D.4∶1‎ ‎3.在比例尺为的地图上，量得两地的距离是，则这两地的实际距离 是（ ）‎ ‎ A． B. C. D. ‎4.如图，在△中，为边上一点，∠∠，，，则的长为（　　）‎ A.1 B.4 C.3 D.2‎ ‎5.如图，在△中，点分别是的中点，则下列结论：①；②△∽△；③.其中正确的有（ ）‎ A.3个 B.2个　　　 C.1个 D.0个 ‎6.如图，//，//，分别交于点，则图中共有相似三角形（ ）‎ A.4对 B.5对 C. 6对 D.7对 ‎7.如图，已知△，则下列4个三角形中，与△相似的是（ ）‎ ‎ ‎ ‎8.如图，在□ABCD中，点E是边AD的中点，EC交对角线 ‎ BD于点F，则EF︰FC等于（ ）‎ A.3︰2 B.3︰1 ‎ C.1︰1 D.1︰2‎ 第8题图 ‎9.如图，点是线段的黄金分割点，则下列结论中正确的是（　　）‎ A. B. C. D. 第10题图 ‎ F ‎ G ‎ H ‎ M ‎ N ‎ A ‎ B ‎ C ‎ D ‎ E ‎ ‎10．如图，正五边形是由正五边形经过位似变换得到的，若，‎ 则下列结论正确的是( )‎ A. B. C. D. ‎ 二、填空题（每小题3分，共24分）‎ ‎11.已知，且，则_______.‎ ‎12.如果一个三角形的三边长为5、12、13，与其相似的三角形的最长的边为39，那么较大的三角形的周长为_______，面积为________．‎ ‎13.如图，在△中，∥，，则______．‎ ‎14.若，则=__________.‎ ‎ ‎ 第13题图 第15题图 ‎15.如图，是的黄金分割点，，以为边的正方形的面积为，以 为边的矩形的面积为，则_______（填“＞”“＜”“=”）．‎ ‎16.五边形∽五边形，，，，，________. ‎17.如图，在△ABC中，DE∥BC,,△ADE的面积是8，则△ABC的面积为 .‎ 第18题图 第17题图 ‎18.如图，线段AB两个端点的坐标分别为A(6，6)，B(8，2)，以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C的坐标为 .‎ 三、解答题（共46分）‎ ‎19.（6分）已知：如图，是上一点，∥，，分别交于点，∠1=∠2，探索线段之间的关系，并说明理由.‎ ‎20.（6分）某一天，小明和小亮来到一河边，想用遮阳帽和皮尺测量这条河的大致宽度，两人在确保无安全隐患的情况下，先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).‎ ①小明在B点面向树的方向站好，调整帽檐，使视线通过帽檐正好落在树的底部点D处，如图所示，这时小亮测得小明眼睛距地面的距离AB=1.7米；②小明站在原地转动180°后蹲下，并保持原来的观察姿态（除身体重心下移外，其他姿态均不变），这时视线通过帽檐落在了DB延长线上的点E处，此时小亮测得BE=9.6米，小明的眼睛距地面的距离CB=1.2米.‎ 第20题图 根据以上测量过程及测量数据，请你求出河宽BD是多少米？‎ ‎21.（6分）已知：如图，在△中，∥，点在边上，与相交于点，且∠．求证：（1）△∽△；（2） B ‎ C ‎ A ‎ D ‎ E ‎ F ‎ G ‎ 第21题图 ‎22．（7分）如图，在正方形中，分别是边上的点， 连接并延长交的延长线于点 Ac E ‎ Dc F ‎ B Cc G 第22题图 ‎（1）求证：；‎ ‎（2）若正方形的边长为4，求的长．‎ ‎23．(7分) 如图，为线段的中点，与交于点，∠∠∠且交于点F，交于．写出图中两对相似三角形，并证明其中的一对.‎ A ‎ B ‎ M ‎ F ‎ G ‎ D ‎ E ‎ C ‎ 第23题图 ‎ ‎24.（7分）如图，梯形中，∥，点在上，连接并延长与的延长线交于点．‎ ‎（1）求证：△∽△； ‎ ‎（2）当点是的中点时，过点作∥交于点，若求 的长．‎ ‎25.(7分)如图，是的直径，是上的两点，且，的延长线与的延长线交于点．‎ ‎（1）求证：△∽△；‎ ‎（2）若，，求的长．‎ ‎ ‎ 参考答案 一、选择题 ‎1.D 解析：根据相似图形的定义知，A、B、C项都为相似图形，D项中一个是等边三角形，一个是直角三角形，不是相似图形.‎ ‎2.C 解析：根据相似三角形的面积比等于相似比的平方的性质直接得出结果.△ABC与△A′B′C′的面积的比为1∶4.故选C.‎ ‎3.D 解析： ‎4.D 解析：∵ 在△中，为边上一点，，，‎ ‎∴ △∽△，∴ .‎ 又∵ ，，∴ ,∴ ．‎ ‎5.A 解析：因为点分别是的中点，所以是△的中位线.由中位线的性质可推出①②③全部正确.‎ ‎6.C 解析：△∽△∽△∽△.‎ ‎7.C 解析：由对照四个选项知，C项中的三角形与△相似.‎ ‎8.D 解析：∵ AD∥BC，∴ ，，‎ ‎∴ △DEF∽△BCF，∴ .‎ 又∵，∴ ，∴ ‎ ‎9.C 解析：根据黄金分割的定义可知，．‎ ‎10.B 解析：由正五边形是由正五边形经过位似变换得到的，知，所以选项B正确.‎ 二、填空题 ‎11.4 解析：因为，所以设 所以，所以所以 ‎12.90 270 解析：设另一三角形的其他两边为由题意得，所以 又因为所以三角形是直角三角形，所以周长为 ‎13.9 解析：在△中，因为∥，所以∠∠∠ ∠，所以△∽△，所以，所以，所以 ‎14. 解析：由，得，，，所以 ‎15. 解析：由黄金分割的概念知，又所以所以．‎ ‎16. 解析：因为五边形∽五边形 所以 又因为五边形的内角和为所以.‎ ‎17.18 解析：∵ DE∥BC,∴△ADE∽△ABC，∴ .‎ ‎∵ △ADE的面积为8，∴ 解得=18.‎ ‎18.(3，3) 解析：因为，所以点A（6，6）经过缩小变换后点C的坐标为(3，3).‎ 三、解答题 ‎19.解：. 理由如下：‎ ‎∵ ∥∴ ∠∠.‎ 又∴ .‎ 又∵ ∴ △∽△，‎ ‎∴ 即.‎ ‎20.解：由题意，知∠BAD=∠BCE.∵ ∠ABD=∠ABE=90°，‎ ‎∴ △BAD∽△BCE.∴ ，‎ ‎∴ .∴ BD=13.6.‎ ‎∴ 河宽BD是13.6米.‎ ‎21.证明：（1）∵，∴ ∠．‎ ‎∵∥，∴ ，．‎ ‎∴． ‎ ‎∵，∴△∽△． ‎ ‎ （2）由△∽△，得，∴ ． ‎ 由△∽△，得．‎ ‎∵∠∠，∴ △∽△．∴．‎ ‎∴． ∴ ． ‎ ‎22.（1）证明：在正方形中，，.‎ ‎∵ ∴ ，‎ ‎∴ ，∴.‎ ‎（2）解：∵ ∴ .‎ 由（1）知，∴ ，‎ ‎∴.‎ 由∥，得，∴ △∽△，‎ ‎∴，∴.‎ ‎23.解：△∽△，△∽△，△∽△（写出两对即可）.‎ 以下证明△∽△．‎ ‎∵ ∠＝∠＋∠＝∠＋∠＝∠，∠＝∠，‎ ‎∴ △∽△．‎ ‎24. （1）证明：∵ 梯形中，∥，∴ ‎∴ △∽△． ‎ ‎ （2）解： 由（1）知，△∽△，‎ 又是的中点，∴ ‎∴△≌△ ∴ 又∵ ∥∥，‎ ‎∴ ∥，得． ‎ ‎ ∴ ‎∴ ．‎ ‎25.（1）证明：∵ ，∴ ．‎ ‎∴ ∠∠．‎ 又∠∠，∴ △∽△． （2）解：∵ △∽△，∴ ．‎ ‎∵ ，，∴ ．‎ ‎∴ ．∴ ． ‎ ‎∵ 是的直径，∴ ∠°．‎ 在Rt△中，∴ ．‎ 沪科版九年级数学上册第23章测试题 ‎（时间：90分钟 分值：100分）‎ 一、选择题.(每小题4分，共32分)‎ ‎1.如图，在Rt△ABC中，∠BAC=90°,AD⊥BC于点D，则下列结论不正确的是（ ）‎ A.sinB= B.sinB=‎ C.sinB= D.sinB=‎ ‎2.已知沿一山坡水平方向前进40米，在竖直方向上就升高20米，那么这个山坡的坡度是（ ）‎ A.1∶2 B.2∶1 C.1∶ D.∶1‎ ‎3.锐角A满足cosA=，利用计算器求∠A时，依次按键 则计算器上显示的结果是（ ）‎ A.30° B.45° C.60° D.75°‎ ‎4.如图是某商场一楼与二楼之间的手扶电梯示意图．其中AB、CD分别表示一楼、二楼地面的水平线，∠ABC=150°，BC的长是8m，则乘电梯从点B到点C上升的高度h是（ ）‎ A.m B.4m C.m D.8m ‎ ‎ 第4题图 第5题图 ‎5.如图，∠1的正切值是（ ）‎ A.2 B. C. D.‎ ‎6.如图，在网格中，小正方形的边长均为1，点A、B、C都在格点上，则∠ABC的正切值是（ ）‎ A.2 B. C. D.‎ ‎ ‎ 第6题图 第8题图 ‎7.如果+|tanB－3|=0,那么对△ABC 的形状描述最准确的是（ ）‎ A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形 ‎8.如图，若锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），则下列三个结论：①sinC>sinD；②cosC>cosD；③tanC>tanD中，正确的结论为（ ）‎ A.①② B.②③ C.①②③ D.①③‎ 二、填空题.(每小题4分，共32分)‎ ‎9.在Rt△ABC中，∠C=90°，a=31，c=31，则∠A= 度，∠B= 度，b= ．‎ ‎10.如图，某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B，如果AB=2000米，则他实际上升了 米.‎ ‎ ‎ 第10题图 第11题图 ‎11.如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα=32，则t的值是 .‎ ‎12.已知传送带与水平面所成斜坡的坡度i=1:2.4，如果它把物体送到离地面10米高的地方，那么物体所经过的路程为 米．‎ ‎13.（四川南充中考）如图，正方形ABCD的边长为2，过点A作AE⊥AC，AE=1，连接BE，则tanE= .‎ ‎ ‎ ‎ ‎ 第13题图 第14题图 ‎14.如图，在一次数学课外实践活动中，小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°，测角仪高AD为1m，则旗杆高BC为 m（结果保留根号）‎ ‎15.如图，在△ABC中，AB=AC=5，BC=8．若∠BPC=∠BAC，则tan∠BPC ‎= ．‎ ‎ ‎ 第15题图 第16题图 ‎16.如图，A市气象局预报：一沙尘暴中心在A市正西方向1000km的B处，正迅速向北偏东60°的BC方向移动，距沙尘暴中心400km的范围内为受沙尘暴影响的区域，根据所学过的知识，你认为A市 （填“会”或“不会”）受这次沙尘暴的影响．‎ 三、解答题.(共56分)‎ ‎17.（6分）计算：‎ ‎（1）tan30°·cos30°+sin260°－cos245°·tan45°；‎ ‎（2）tan245°+－3sin260°+tan45°sin30°.‎ ‎18.（6分）解直角三角形：‎ ‎（1）在Rt△ABC中，∠C=90°，a=5，c=13，求sinA，cosA，tanA；‎ ‎（2）Rt△ABC的斜边AB=5，cosA=0.5，求△ABC的其他元素．‎ ‎19.（6分）如图，某校数学兴趣小组为测得校园里旗杆AB的高度，在操场的平地上选择一点C，测得旗杆顶端A的仰角为30°，再向旗杆的方向前进16米，到达点D处（C、D、B三点在同一直线上），又测得旗杆顶端A的仰角为45°，请计算旗杆AB的高度.（结果保留根号）‎ ‎20.（8分）如图，在△ABC中，已知∠C=90°，sinA=，D为边AC上一点，∠BDC=45°，DC=6．求△ABC的面积．（结果保留根号）‎ ‎21.(8分)A，B两市相距150千米，分别从A，B处测得国家级风景区中心C处的方向角如图所示，风景区区域是以C为圆心，45千米为半径的圆，tanα=1.627，tanβ=1.373.为了开发旅游，有关部门设计修建连接A，B两市的高速公路.问连接A，B的高速公路是否穿过风景区？请说明理由.‎ ‎22.（10分）如图所示，△ABC内接于⊙O，AB是⊙O的直径，点D在⊙O上，连接CD且DC=BC，过C点作AD的垂线交AD延长线于E.‎ ‎（1）求证：CE是⊙O的切线；‎ ‎（2）若AB=5，AC=4，求tan∠DCE的值．‎ ‎23.（12分）某校吴老师组织九(1)班同学开展数学活动，带领同学们测量学校附近一电线杆的高，已知电线杆直立于地面上，某天在太阳光的照射下，电线杆的影子（折线BCD）恰好落在水平地面和斜坡上，在D处测得电线杆顶端A的仰角为30°，在C处测得电线杆顶端A的仰角为45°.斜坡与地面成60°角，CD=4m，请你根据这些数据求电线杆的高.(结果精确到1m，参考数据：≈1.4，≈1.7)‎ 参考答案