- 2021-11-11 发布 |
- 37.5 KB |
- 3页


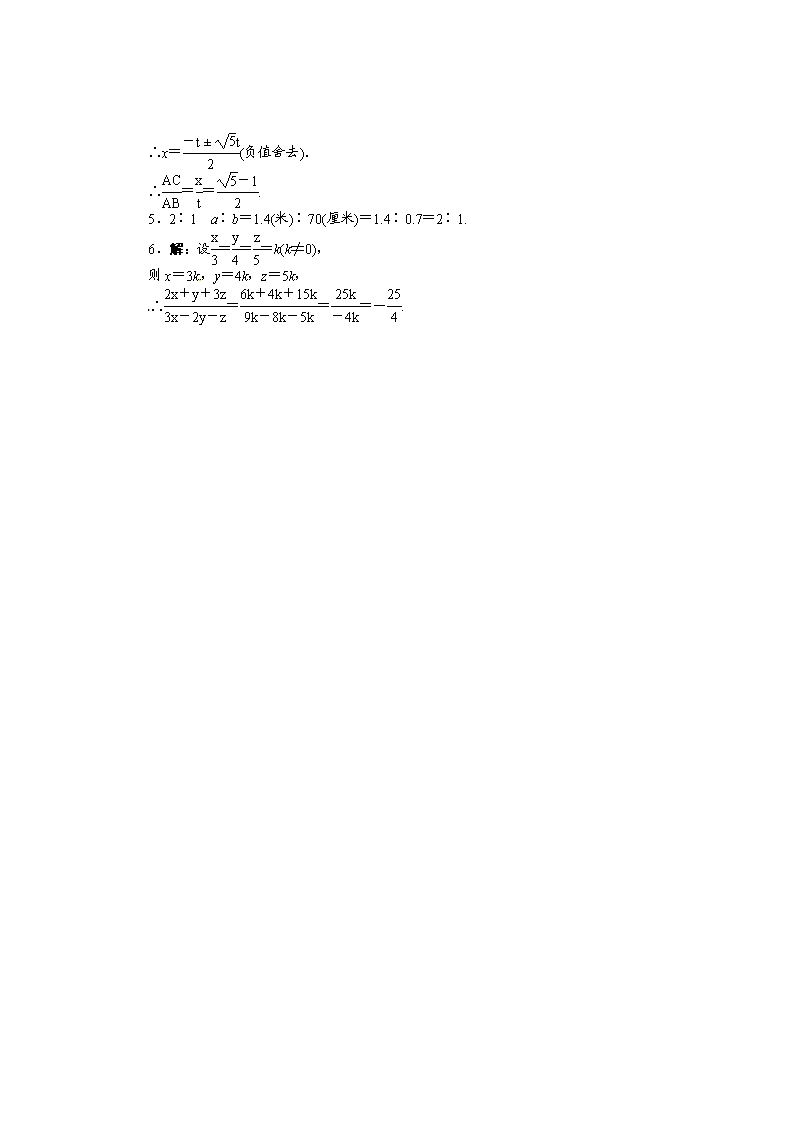
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级上数学(华师大版)导学案-231成比例线段
24.2 相似图形的性质 第1课时 成比例线段 学前温故 如图,△ABC≌△DEF,则AB=DE,AC=DF,BC=EF,即===____. 新课早知 1.对于四条线段a、b、c、d,如果其中两条线段的长度的比等于另外两条线段的比,如________(或________),那么,这四条线段叫做成比例线段. 2.下列各组线段成比例的是( ). A.2 cm,3 cm,4 cm,5 cm B.1.5 cm,2.5 cm,4.5 cm,6.5 cm[来源:学科网ZXXK] C.1 cm,2.2 cm,3.3 cm,4.4 cm D.1 cm,2 cm,2 cm,4 cm 3.(1)如果=,那么______. (2)如果ad=bc(a、b、c、d都不等于0),那么________. 4.已知线段a=4,b=6,c=8,线段a、b、c、d成比例,则d等于__________. 5.如果2∶3=(5-x)∶x,那么x=__________. [来源:学科网] 答案:学前温故 1 新课早知 1.= a∶b=c∶d 2.D 3.(1)ad=bc (2)= 4.12 5.3 1.成比例线段 【例1】 判断下列各组线段是否成比例. (1)4 cm,2 cm,1 cm,3 cm; (2)1 cm,2 cm,20 mm,4 cm. 分析:利用成比例线段的定义解,但要注意将四条线段统一单位. 解:(1)∵≠,∴这四条线段不成比例.[来源:Zxxk.Com] (2)∵=,∴这四条线段成比例.[来源:学科网ZXXK] 点拨:判断四条线段成比例,比较简捷的方法是把它们按大小顺序排好,看前两条线段之比与后两条线段之比是否相等,或者看最长和最短线段长度的乘积与中间两线段长度的乘积是否相等. 2.比例的性质及应用 【例2】 已知a∶b∶c=4∶3∶2,且a+2b-3c=12,求: (1)a、b、c的值; (2)3a-2b+c的值. 分析:根据比的意义,用设比值的方法求解.[来源:学科网ZXXK] 解:∵a∶b∶c=4∶3∶2,∴==. 设===k(k≠0), 则a=4k,b=3k,c=2k, ∴a+2b-3c=4k+6k-6k=4k=12.∴k=3. ∴(1)a=12,b=9,c=6; (2)3a-2b+c=3×12-2×9+6=24. 点拨:对于与比例有关的题目,除用比例的基本性质外,一般用设比值法,利用这种方法可解决有关比例的计算题. 1.(2010福建德化中考)下列各组线段(单位:cm)中,成比例线段的是( ). A.1、2、3、4 B.1、2、2、4 C.3、5、9、13 D.1、2、2、3 2.下列说法中正确的有( ). ①两条线段的比是两条线段长度之比,比值是一个正数;②两条线段的长度比是“同一单位下”的长度比;③两条线段的比与所采用的长度单位无关;④两条线段的比有顺序,与不同,它们互为倒数. A.1个 B.2个 C.3个 D.4个 3.若=,则下列各式中不正确的是 ( ). A.= B.=4 C.= D.= 4.如图,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C黄金分割,AC与AB的比叫做黄金比,其比值是( ). A. B. C. D. 5.已知一矩形的长a=1.4米,宽b=70厘米,那么a∶b=__________. 6.若==,求的值. 答案:1.B 2.D 3.D 4.A 设AC=x,AB=t, 则BC=t-x, 由已知得AC2=AB·BC, 即x2=t(t-x), ∴x2+tx-t2=0. ∴x=(负值舍去). ∴==. 5.2∶1 a∶b=1.4(米)∶70(厘米)=1.4∶0.7=2∶1. 6.解:设===k(k≠0), 则x=3k,y=4k,z=5k, ∴===-.查看更多