- 2021-11-11 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年福建省厦门市五校九年级上期中联考数学试卷含答案
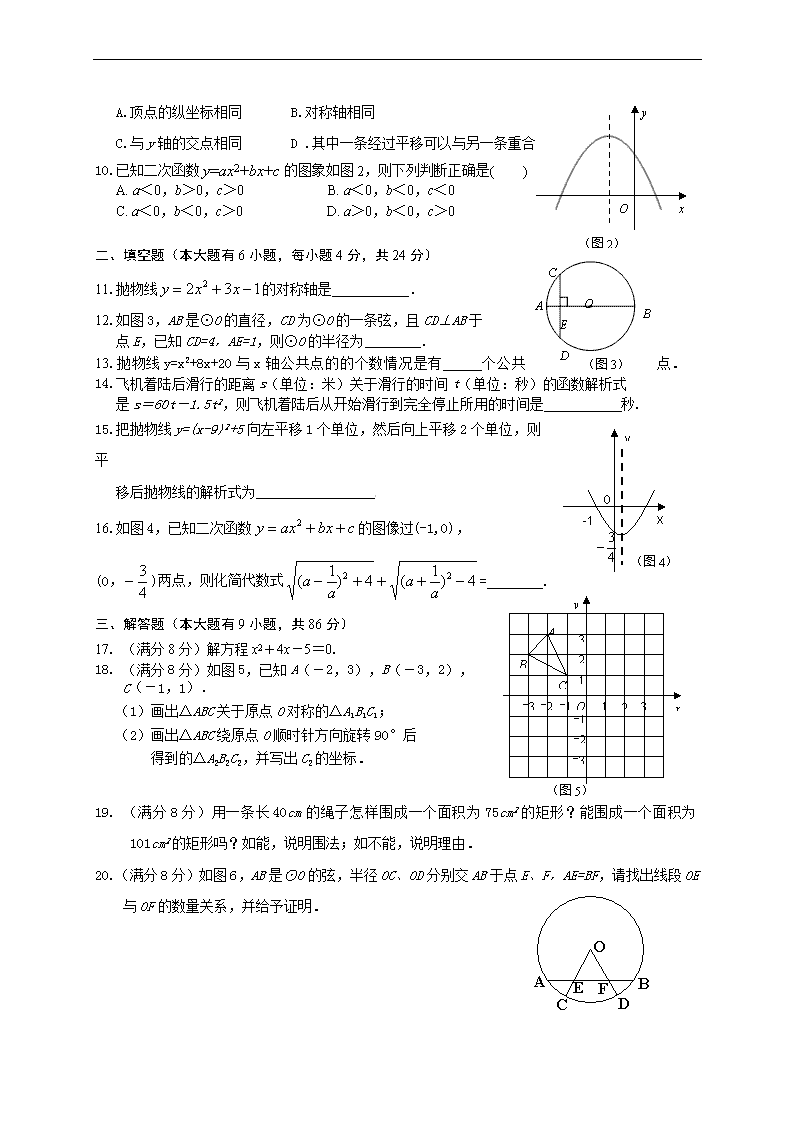
2017—2018学年(上)图3 九年级期中联考 数 学 (试卷满分:150分 考试时间:120分钟) 准考证号 姓名 座位号 联考学校:凤南中学、梧侣学校、厦门市第二外国语学校等五校 一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确) 1.已知点,点A关于原点的对称点是,则点的坐标是( ) A. B. C. D . 2.下面的图形中,既是轴对称图形又是中心对称图形的是( ) A. B. C. D.21世纪教育网版权所有 3.方程x2=4的解是( ) A. B. C. D. 4.一元二次方程的根的情况是( ) A.有两个不相等的实数根 B.有两个相等的实数根 C.只有一个实数根 D.没有实数根 5.用配方法解方程,下列配方结果正确的是( ) A. B. C. D. 6.已知△ABC和△DEF关于点O对称,相应的对称点如图1所示, 则下列结论正确的是( ) A. AO=BO B. BO=EO 图1 C. 点A关于点O的对称点是点D D.点D 在BO的延长线上 7.对抛物线描述正确的是( ) A. 开口向下,顶点坐标是(7,-6) B. 开口向上,顶点坐标是(-7,6) C. 开口向下,顶点坐标是(-7,-6) D. 开口向上,顶点坐标是(-7,-6) 8.已知点(-1,y1),(4,y2),(5,y3)都在抛物线y=(x-3)2+k上,则y1,y2,y3的大小关系为( ) A.y1<y2<y3 B. y1<y3<y2 C. y1>y2>y3 D. y1>y3>y2 9.已知抛物线y=ax2+bx+c和y=max2+mbx+mc,其中a,b,c,m均为正数, 且m≠1.则关于这两条抛物线,下列判断正确的是( ) (图2) O x y A.顶点的纵坐标相同 B.对称轴相同 C.与y轴的交点相同 D .其中一条经过平移可以与另一条重合 10.已知二次函数y=ax2+bx+c的图象如图2,则下列判断正确是( ) A. a<0,b>0,c>0 B. a<0,b<0,c<0 C. a<0,b<0,c>0 D. a>0,b<0,c>0 CA 二、填空题(本大题有6小题,每小题4分,共24分) E OA BA DA A 11.抛物线的对称轴是 . 12.如图3,AB是⊙O的直径,CD为⊙O的一条弦,且CD⊥AB于 (图3) 点E,已知CD=4,AE=1,则⊙O的半径为 . 13.抛物线y=x2+8x+20与x轴公共点的的个数情况是有 个公共点. 14.飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式 是s=60t-1.5t2,则飞机着陆后从开始滑行到完全停止所用的时间是 秒. y x -1 O 15.把抛物线y=(x-9)2+5向左平移1个单位,然后向上平移2个单位,则平 移后抛物线的解析式为 (图4) 16.如图4,已知二次函数的图像过(-1,0), (图5) y x O 1 2 3 1 2 3 -3 -2 -1 -1 -2 -3 A B C (0,)两点,则化简代数式= . 三、解答题(本大题有9小题,共86分) 17. (满分8分)解方程x2+4x-5=0. 18. (满分8分)如图5,已知A(-2,3),B(-3,2),[来源:学+科+网] C(-1,1). (1)画出△ABC关于原点O对称的△A1B1C1; (2)画出△ABC绕原点O顺时针方向旋转90°后 得到的△A2B2C2,并写出C2的坐标. 19. (满分8分)用一条长40cm的绳子怎样围成一个面积为75cm2的矩形?能围成一个面积为101cm2的矩形吗?如能,说明围法;如不能,说明理由. 20.(满分8分)如图6,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,AE=BF,请找出线段OE与OF的数量关系,并给予证明. 图6 21. (满分8分)已知抛物线的顶点为(1,4),与y轴交点为(0,3) (1)求该抛物线的解析式,并画出此函数的图像; (2)观察图像,写出当y<0时,自变量x的取值范围。 22. (满分10分)如图7,已知在矩形ABCD中,∠ADC的平分线DE与BC边交于点E,点P是线段DE上一定点(其中EP<PD). 若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交线段DA于点H、G.21cnjy.com A B C D E F G H P (1) 求证:PG=PF; (2) 探究:DF、DG、DP之间有怎样的数量关系,并证明 你的结论. 图7 [来源:学科网ZXXK] 23. (满分10分)已知关于x的方程有两个不相等的实数根, (1)求的取值范围 (2)试说明<0,<0 (3)若抛物线与轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OA·OB-3,求的值.www.21-cn-jy.com 24.(满分12分)定义:若抛物线:(m≠0)与抛物线:(a≠0)的开口大小相同,方向相反,且抛物线经过的顶点,我们称抛物线为的“友好抛物线”. (1)若的表达式为,求的“友好抛物线”的表达式;(5分) (2)平面上有点P (1,0),Q (3,0),抛物线:为:的“友好抛物线”,且抛物线的顶点在第一象限,纵坐标为2,当抛物线与线段PQ没有公共点时,求a的取值范围.(7分) 2·1·c·n·j·y 25. (满分14分)如图8,抛物线与轴交于A、B两点,与轴交于点C ,抛物线的对称轴交轴于点D,已知A(-1,0),C(0,2) .【来源:21·世纪·教育·网】 (1)求抛物线的解析式; (2)点E是线段BC上的一个动点(不与B、C重合),过点E作轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标。21·世纪*教育网 (3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由.w 2017—2018学年(上)图3 九年级期中联考 数学科 评分标准 一、选择题: 题次[来源:学&科&网Z&X&X&K] 1 2 3 4 5 6 7 8 9 10 答案 A B D B B D C D B C 二、 填空题: 11. 直线 12. 13. 0 14. 20 15. y=(x-8)2+7 16. 三、 解答题: 17.解:x2+4x-5=0 b2-4ac=42-4×(-5)=36 ……………………………2分 ……………………………3分 = ……………………………5分 = ……………………………6分 ,……………………………8分 说明:☆本题亦可用因式分解法和配方法求解. ☆写出正确答案(即写出x1=,x2=,)且至少有一步过程,不扣分. ☆只有正确答案,没有过程,只扣1分. (图5) y x O 1 2 3 1 2 3 -3 -2 -1 -1 -2 -3 A B C B1 A1 C1 C2 A2 B2 ☆ 如果没有化简(即,),只扣1分. 18.解:正确画出△A1B1C1 . ………………3分 正确画出△A2B2C2., ………………6分 正确写出点C2坐标(-1,-1)………7分 ∴△A1B1C1和△A2B2C2如图为所求.…8分 点的字母标错或没下结论最后一分不得分. 19. 解:设该矩形的一边长为x cm,则另一边长为(20-x) cm…………………1分 依题意得: …………………2分 解得: …………………3分 经检验:都符合题意 ∴另一边长20-x=15或5…………………4分 若矩形的面积=101 cm2,依题意得: 整理得: ……………5分 b2-4ac=400-404=-4<0…………6分 ∴该方程无实根……………7分2-1-c-n-j-y ∴不能围成一个面积为101cm2的矩形.……………8分 答:当矩形的边长为5cm和15cm时面积是75cm2,不能围成一个面积为101cm2的矩形. 20.解:OE=OF 理由如下:过点O作OH⊥AB于点H……………1分 ∵OH过圆心,OH⊥AB H ∴AH=BH……………4分 又∵AE=BF 图6 ∴AH-AE=BH-BE[来源:学科网ZXXK] 即EH=FH……………5分 ∵EH=FH,OH⊥EF ∴OH垂直平分EF……………7分 ∴OE=OF……………8分 说明:☆垂径定理的条件(OH过圆心,OH⊥AB)少一个条件扣一分. 21.解: 设抛物线解析式为…………1分 将(0,3)代入得…………2分 解得…………3分 ∴该抛物线解析式为…………4分 列表,描点,连线…………6分 观察图像可知:当y<0时,自变量x的取值范围是x<-1或x>3……8分 22.解:(1)证明:∵四边形ABCD是矩形∴∠ADC=90° A B C D E F G H P (图7) ∵DE平分∠ADC,∴∠PDF=∠ADP=45°…………………1分 由旋转可知∠GPF=∠HPD=90°…………………2分 ∴∠GPH=∠FPD ………3分 ∵∠HPD=90°,∠ADP=45°[来源:Zxxk.Com] ∴△HPD为等腰直角三角形 ……4分 ∴∠DHP=∠PDF=45°且PH=PD ………………5分 ∴△HPG≌△DPF ∴PG=PF …………………………………………6分 (2)结论:……………7分 证明:∵△HPD为等腰直角三角形, ∴ HD2=2, ∴……………………………………………………8分 ∵△HPG≌△DPF ∴DF=HG……………………………………………………9分 ∴,∴ ………………10分 23、解:(1)∵方程有两个不相等的实数根 ∴=-12k+5>0, ∴k<……………………2分 (2)由可知 o x y A B x1 x2 ,……………………3分 ∵>0 ∴和同号……………4分 ∵k<∴< ∴<0 ∴<0,<0……………5分 (3)如图设A(x1,0)B(x2,0) ∴OA+OB=-x1+(-x2)=-(x1+x2)=3-2k, OA·OB=-x1·(-x2)= ……7分 ∴……8分 解得……9分 又∵k<∴……10分 24.解:(1)依题意,可设的“友好抛物线”的解析式为:,…1分 ∵:, ∴的顶点为(1,-1). ……………3分 ∵过点(1,-1),∴,即b=0. …………4分 ∴的“友好抛物线”为:. ……………5分 (2)依题意,得 m =-a. ∴:的顶点为. ……………7分 ∴,即. ……………8分 当经过点P(1,0)时, ,∴a=8. ……………9分 当经过点Q(3,0)时, ,∴. ……………10分 ∴抛物线与线段PQ没有公共点时,或. ……12分 25.解:(1)将A(-1,0),C(0,2)代入抛物线解析式得 解得 ∴抛物线解析式为 ………………………………2分 (2)由 可知对称轴为直线 ∴D(,0) …………3分 令y=0,则 解得 ∴B(4,0) ………………………4分 H E F x y o A C B D 设直线BC的解析式为y=kx+b, 将B、C点坐标代入得,解得 ∴直线BC的解析式为………………………5分 设F(x,y),EF⊥x轴于点H,则H(x,0) ∴梯形COHF的面积S1= Rt△BHF的面积S2= Rt△OCD的面积S3= ∴四边形CDBF的面积S=S1+S2-S3= 又∵F在抛物线上 ∴将 代入S得S=………8分 ∵S是关于x的二次函数,a=-1<0 ∴当x=2时,S有最大值为………9分 此时E点的横坐标x=2………10分 ∵E点在直线BC上 ∴ ∴E(2,1) ………11分 (3)P点坐标为(,)(,)(,-4) ………14分 图8 备用图查看更多